多电子原子轨道能级
- 格式:ppt
- 大小:2.20 MB
- 文档页数:76


原子轨道能和原子轨道能级的关系一、原子轨道能原子轨道是描述原子中电子分布位置的概念,而原子轨道能则是指电子在这些轨道上所具有的能量。
1.1 原子轨道能的计算原子轨道能可以通过求解薛定谔方程得到。
薛定谔方程是描述物质微粒波函数随时间变化的方程,利用薛定谔方程可以得到电子在原子中的波函数,而波函数的平方则给出了电子在不同位置上出现的概率密度。
通过对波函数的计算和分析,可以得到不同原子轨道上电子的能量,并将其表示为原子轨道能。
1.2 原子轨道能的特点原子轨道能具有以下几个特点:- 不同轨道有不同的能量。
在简并的情况下(即具有相同能量的轨道),轨道能可以相等;在非简并的情况下,轨道能必定是不同的。
- 轨道能随着原子核电荷数的增加而降低。
原子核的电荷数增加会增加核吸引电子的能力,导致电子的能量降低。
1.3 原子轨道能的计算方法原子轨道能的计算方法有多种,主要包括量子化学方法、密度泛函理论和巴特勒-施威克近似等。
这些方法可以对原子轨道能进行定量计算和分析,为理解原子内部电子分布和化学行为提供了重要的理论基础。
二、原子轨道能级原子轨道能级是指原子轨道在能量上的分层结构,不同能级上的轨道能量不同,代表了电子在原子中的不同分布状态。
2.1 原子轨道能级的表示方法原子轨道能级通常使用能量量子数和角动量量子数来表示。
能量量子数n表示了原子轨道能级的大小,而角动量量子数l则表示了轨道的角动量大小。
通过这两个量子数的组合可以确定原子轨道的具体能级。
2.2 原子轨道能级的性质原子轨道能级具有以下几个主要性质:- 能级数目受限。
根据量子力学的理论,原子轨道能级的数量是有限的,每个能级上能容纳的电子数也是有限的。
- 能级间隔不等。
原子轨道能级之间的能量差异并不是固定的,不同的能级间隔是不同的。
- 能级分布规律性。
原子轨道能级的分布遵循一定的规律,如经典的玻尔模型可以用来解释氢原子的能级分布。
2.3 原子轨道能级的应用原子轨道能级的描述和理解对于原子光谱、化学键形成和化学反应机理等方面都具有重要意义。
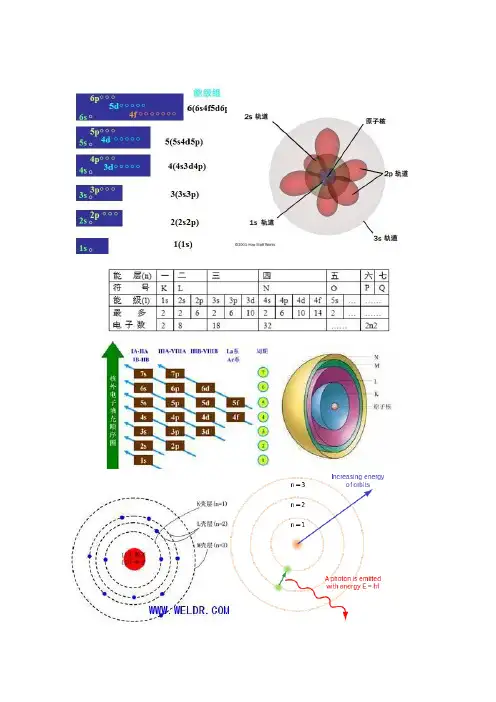
原子轨道近似能级图编辑美国化学家Pauling经过计算,将原子轨道分为七个能级组。
第一组:1s第二组:2s2p第三组:3s3p第四组:4s3d4p第亓组:5s4d5p第六组:6s4f5d6p第七组:7s5f6d7p特点:1、能级能量由低到高。
2、组与组之间能量差大,组内各轨道间能量差小,随n逐渐增大,这两种能量差逐渐减小。
3、第一能级组只有1s一个轨道,其余均有两个或两个以上,且以ns开始np结束。
4、能级组与元素周期相对应。
如题:最近有人问我XPS元素的右下角数字的含义。
这是我个人的理解,请大家多多指教。
1、四个量子数的物理意义:n为主量子数;l为角量子数;m为磁量子数;s为自旋量子数。
n=1,2,3,4…,但不等于0,并且以K(n=1),L(n=2),M(n=3),N(n=4),…表示。
l=0,1,2,3…。
并且以s(l=0),p(l=1),d(l=2),f(l=3),…表示。
s=1/2m=0,±1, ±2,…, ±l2、自旋-轨道分裂我们知道原子中的电子既有轨道运动又有自旋运动。
量子力学的理论和光谱试验的结果都已经证实电子的轨道运动和自旋运动之间存在着电磁相互作用。
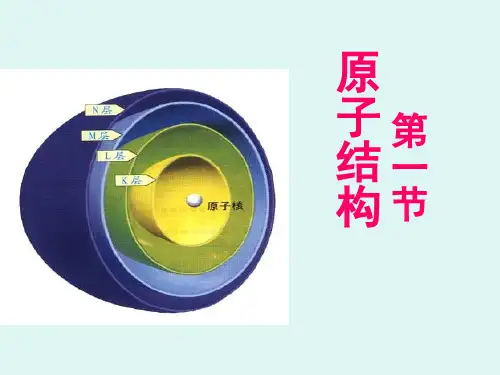
自旋-轨道耦合的结果使其能级发生分裂,这种分裂可以用总量子数j来表示,其数值为:j=l+s, l+s-1,…,|l-s|由上式可以知道:s轨道:当l=0,s=1/2时,j只有一个数值,即j=1/2;p轨道:当l=1,s=1/2时,j=1/2,3/2d轨道:当l=2,s=1/2时,j=3/2,5/2f轨道当l=3,s=1/2时,j=5/2,7/23、原子和分子轨道的符号表示原子中内层电子的运动状态可以用以描述单个电子运动状态的四个量子数来表征。
电子能谱试验通常是在无外磁场作用下进行的,磁量子数m是简并的,所以在电子能谱研究中通常用n,l,j三个量子数来表征内层电子的运动状态。
价电子用分子轨道符号来表示。


多电子原子轨道能级顺序
随着互联网技术的发展,人们越来越了解多电子原子的轨道能级顺序。
多电子原子的轨道能级顺序是根据原子电子的层数、电子总数和原子质量等构成的。
原子轨道能级顺序是根据基态能量来定义的,基态能量通常是由原子总能量通过发射光子而释放的,其顺序是从低到高依次分别排列。
原子的轨道能级顺序是由外层电子向内层移动的,从最外层的K能级开始,然后K、L、M、N四级能级依次向内排列,再然后依次是O、P、Q、R五级能级最后到达原子中心。
原子内部由原子质量构成,原子质量越大,原子轨道能级顺序也会相应变得更复杂。
特别地,由于原子质量至少为十二以上,它们的能级顺序将需要更多的电子层依次排列,而每一层中可能存在多个电子。
另外,根据四率定律,当原子能够发射分子,它将会释放出一个更高的能级,以及更多的光子来作为分子的“礼物”。
以上是关于多电子原子的轨道能级顺序的介绍,根据原子电子的层数、电子总数和原子质量等特点,多电子原子的轨道能级顺序由低到高依次排列,而且随着原子质量的增加,轨道能级也变得更加复杂。
因此,了解多电子原子轨道能级顺序对于研究原子性质有重要意义。

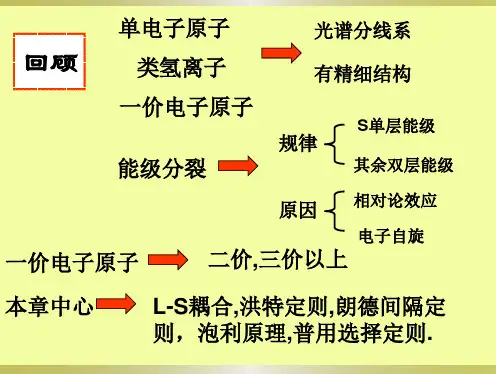


能层-能级-原子轨道之间啥关系
能层、能级和原子轨道都是描述原子结构的概念。
一个原子的电子会占据不同能级,每个能级被分成许多不同的能层,一个能层可以包含一到多个能级。
能级决定了原子中的电子能够具有的能量范围,并且能够在不同能级之间跃迁。
而能级的位置决定了电子在原子轨道中的分布,原子轨道是一种描述电子分布空间的函数,用于描述一个电子在原子中运动的概率。
因此,能层、能级和原子轨道之间存在着密切的关系,相互作用来描述原子中的电子结构。
第一章原子结构第四节多电子原子结构1.4.1 多电子原子轨道能级由于氢原子和类氢离子核外只有一个电子,它只受到核的作用力。
因此,对于单电子体系, 轨道上的电子的能量,只由主量子数 n 决定: E ns = E np = E nd = E nf = -(Z 2/n 2) 13.6 eV 。
氢原子各轨道能量高低次序◆对于多电子体系,对某一指定的电子来说,它除了受到核的吸引力之外,还受到其他电子的排斥作用。
◆由于多个电子间相互排斥作用的复杂性,多电子原子的薛定谔方程无法精确求解,需寻找近似计算方法,如“中心力场模型”等。
中心力场近似模型:把多电子体系简化为单电子体系,将其他电子对指定电子的作用看作是抵消了部分核电荷的作用,这样可以求得Schrödinger 方程的近似解,得到相应的波函数及轨道能级。
计算表明,波函数的角度部分和单电子原子大致相同,而径向部分和单电子原子不同。
Pauling近似能级图Pauling 根据光谱实验的结果,提出了原子轨道近似能级图。
能级组:将能量相近的能级划为一组七个能级组:1s;2s2p;3s3p;4s 3d 4p;5s 4d 5p;6s4f 5d 6p;7s 5f 6d 7pPauling近似能级图组内能级间能量差小,组间能量差大能级分裂:n 同,l 不同,如:E3s< E3p< E3d 能级交错:n, l 均不同,E4s< E3d徐光宪的能级高低的近似原则:n + 0.7l例如:第四能级组4s < 3d < 4pn + 0.7l 4.0 4.4 4.7第六能级组6s < 4f < 5d < 6pn + 0.7l 6.0 6.1 6.4 6.7 Pauling能级图仅仅反映了多电子原子中原子轨道能量的近似高低,不要误认为所有元素原子的能级高低都是一成不变的。
Cotton 原子轨道能级图Cotton 原子轨道能级图的特点:反映了主量子数相同的氢原子轨道的简并性;反映出原子轨道的能量随着原子序数的增大而降低;反映出随着原子序数的增大,原子轨道能级下降幅度不同,因此能级曲线产生了相交现象。
原子轨道能量13.6原子轨道能量(13.6eV)是指氢原子中电子在各个轨道上的能量值。
这个数值是经过实验测定得出的,并且在原子物理学中具有重要的意义。
本文将以中括号为主题,一步一步回答与原子轨道能量相关的问题。
第一步,我们来了解一下为什么会有原子轨道能量这个概念。
在原子中,电子绕着原子核运动,就好像行星绕着太阳运动一样。
根据量子力学理论,电子的运动状态是量子化的,即只能处于特定的能量级别上。
这些能量级别就是原子轨道。
第二步,我们需要了解如何计算原子轨道的能量。
在氢原子中,原子核只有一个质子,所以只有一个电子绕核旋转。
根据波尔模型,可以用以下公式来计算原子轨道能量:E = -13.6 / n²其中,E是能量,n是主量子数。
主量子数确定了电子所处的轨道级别,取整数值1,2,3,...。
根据这个公式,我们可以计算得出不同轨道上的能量值。
第三步,我们可以具体计算一些例子来进一步理解原子轨道能量。
以氢原子为例,我们可以计算出前几个轨道的能量值:当n等于1时,E = -13.6 / 1²= -13.6 eV当n等于2时,E = -13.6 / 2²= -3.4 eV当n等于3时,E = -13.6 / 3²= -1.51 eV...可以看到,随着主量子数n增加,能量变得更高。
第四步,我们需要理解原子轨道能量对原子性质的影响。
原子轨道能量不仅决定了电子所处的能级,还决定了电子的行为。
当外界能量作用于原子体系时,电子可以发生跃迁,从一个能级跃迁到另一个能级。
这种跃迁过程会产生光谱,成为研究原子结构和物质性质的重要手段。
此外,原子轨道能量还对原子的化学性质产生影响。
在化学反应中,电子的轨道能量决定了能否与其他原子进行化学键的形成。
当两个原子之间的电子轨道能量相近时,它们更容易形成化学键。
反之,如果能级差异过大,可能导致无法形成化学键。
第五步,原子轨道能量的概念不仅适用于氢原子,也适用于其他原子。