高考数学培优理科通用版能力升级练：(九) 空间几何体及三视图 Word版含解析

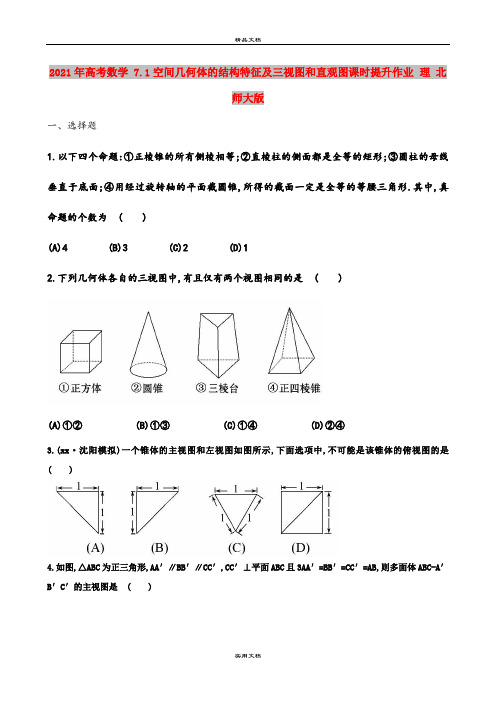
2021年高考数学 7.1空间几何体的结构特征及三视图和直观图课时提升作业理北师大版一、选择题1.以下四个命题:①正棱锥的所有侧棱相等;②直棱柱的侧面都是全等的矩形;③圆柱的母线垂直于底面;④用经过旋转轴的平面截圆锥,所得的截面一定是全等的等腰三角形.其中,真命题的个数为( )(A)4 (B)3 (C)2 (D)12.下列几何体各自的三视图中,有且仅有两个视图相同的是( )(A)①②(B)①③(C)①④(D)②④3.(xx·沈阳模拟)一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是( )4.如图,△ABC为正三角形,AA′∥BB′∥CC′,CC′⊥平面ABC且3AA′=BB′=CC′=AB,则多面体ABC-A′B′C′的主视图是( )5.(xx·宁波模拟)一个水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )(A)+ (B)2+(C)+ (D)+6.一个正方体截去两个角后所得几何体的主视图、左视图如图所示,则其俯视图为( )7.(xx·西安模拟)一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A处出发,经正方体的表面,按最短路线爬行到达顶点C1位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的主视图是( )(A)①②(B)①③(C)②④(D)③④二、填空题8.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为.9.(xx·临沂模拟)已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是cm3,则主视图中的h等于cm.10.(xx·合肥模拟)一个三棱锥的主视图和左视图及其尺寸如图所示,则该三棱锥的俯视图的面积为.三、解答题11.(能力挑战题)如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝.再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).答案解析1.【解析】选B.由正棱锥的定义可知所有侧棱相等,故①正确;由于直棱柱的底面的各边不一定相等,故侧面矩形不一定全等,因此②不正确;由圆柱母线的定义可知③正确;结合圆锥轴截面的作法可知④正确.综上,正确的命题有3个.2.【解析】选D.在各自的三视图中,①正方体的三个视图都相同;②圆锥的两个视图相同;③三棱台的三个视图都不同;④正四棱锥的两个视图相同,故选D.【变式备选】正三棱柱(底面为正三角形的直棱柱)ABC-A 1B1C1如图所示,以四边形ABB1A1为水平面,四边形BCC1B1的前面为正前方画出的三视图正确的是( )【解析】选A.矩形BCC1B1的前面为正前方,故主视图为矩形,左侧为△ABC,所以左视图为三角形.俯视图为两个有公共边的矩形,公共边为CC1在面ABB1A1内的投影,故选A.3.【解析】选C.当俯视图为A,B时表示底面为等腰直角三角形,且过直角顶点的棱与底面垂直的三棱锥.当俯视图为D时,表示底面为正方形,且有一条侧棱与底面垂直的四棱锥.故选C.【方法技巧】由直观图画三视图的技巧(1)可以想象将一几何体放在自己面前,然后从正前方,左侧及上面观察该几何体,进而得到主视图、左视图和俯视图.(2)在画三视图时,要注意看得见的轮廓线画成实线,看不见的轮廓线画成虚线.4.【解析】选D.由AA′∥BB′∥CC′及CC′⊥平面ABC,知AA′⊥平面ABC,BB′⊥平面ABC.又CC′=BB′=3AA′,且△ABC为正三角形,故主视图应为D中的图形.5.【解析】选B.如图将直观图ABCD还原后为直角梯形A′BCD′,其中A′B=2AB=2,BC=1+,A′D′=AD=1,∴S=×(1+1+)×2=2+.6.【解析】选C.依题意可知该几何体的直观图如图所示,故其俯视图应为C.7.【解析】选C.依题意得,题中提供的选项中,图②④可以表示正方体及蚂蚁最短爬行路线的主视图,选C.8.【解析】如图所示,∵OE==1,∴O′E′=,E′F′=,∴直观图A′B′C′D′的面积为S′=×(1+3)×=.答案:9.【解析】由三视图可知,该几何体是一个四棱锥,且底面是一个边长为20cm的正方形,所以V=×20×20×h=,∴h=20(cm).答案:2010.【解析】由题意可知,该三棱锥的俯视图是一个底边长为2,高为1的三角形,则其面积为1.答案:111.【思路点拨】(1)根据条件确定圆柱的高与底面半径的关系,转化为函数问题解决.(2)结合实物图画出三视图即可.【解析】(1)设圆柱的高为h,由题意可知,4(4r+2h)=9.6,即2r+h=1.2.S=2πrh+πr2=πr(2.4-3r)=3π[-(r-0.4)2+0.16],其中0<r<0.6.∴当半径r=0.4米时,S max=0.48π≈1.51(平方米).(2)由r=0.3及2r+h=1.2,得圆柱的高h=0.6(米).则灯笼的三视图为:W' n36458 8E6A 蹪20469 4FF5 俵28421 6F05 漅26189 664D 晍26997 6975 極32971 80CB 胋[/32886 8076 聶30123 75AB 疫D。

专题八立体几何初步第二十二讲空间几何体的三视图、表面积和体积20XX年1.（20XX全国Ⅲ理16）学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体ABCD-A1B1C1D1挖去四棱锥O—EFGH后所得几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，AB=BC=6cm, AA1=4cm，3D打印所用原料密度为0.9 g/cm3，不考虑打印损耗，制作该模型所需原料的质量为___________.2.（20XX江苏9）如图，长方体ABCD-A1B1C1D1的体积是120，E为CC1的中点，则三棱锥E-BCD的体积是 .3.（20XX天津理11）已知四棱锥的底面是边长为2的正方形，侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为 .4.（20XX全国Ⅰ理12）已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为A．86πB．46πC．26πD．6π5.（20XX浙江4）祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高.若某柱体的三视图如图所示，则该柱体的体积是A．158B．162C．182D．326.（20XX北京11）某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示。

如果网格纸上小正方形的边长为1，那么该几何体的体积为________.2010-20XX 年一、选择题1．(20XX 北京)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形2的个数为11正(主)视图2侧(左)视图A．1B．2C．32．(20XX 全国卷Ⅰ)某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为A．217B．25C．3D．2俯视图AD．4B3．(20XX 全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是4．(20XX 全国卷Ⅲ)设A ，B ，C ，D 是同一个半径为4的球的球面上四点，∆ABC 为等边三角形且其面积为93，则三棱锥D -ABC 体积的最大值为A．123B．183C．243D．5435．(20XX 上海)《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马．设AA 1是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以AA 1为底面矩形的一边，则这样的阳马的个数是（）A1三教上人（A+版-Applicable Achives）2A1．1221C A．4B．8D．16侧视图正视图6．(20XX 浙江)某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm 3）是俯视图D．8A．2B．4C．67．（20XX 新课标Ⅰ）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10B．12C．14D．168．（20XX 新课标Ⅱ）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为A．90πB．63πC．42πD．36π9．（20XX 新课标Ⅲ）已知圆柱的高为31，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为11113π正视图ππ侧视图A．πB．C．D．42410．（20XX 浙江）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm 3）是俯视图π3π3ππ+1D．+3+1B．+3C．222211．（20XX 北京）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为A．A．32B．23C．22D．212．（20XX山东）一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为12122 12A．+πB．+πC．+πD．1+π33366 3313．（20XX全国I）如图，某几何体的三视图是三个半径相等的圆及每个圆中两28π条互相垂直的半径，若该几何体的体积是，则它的表面积是3A．17πB．18πC．20πD．28π14．（20XX全国II）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为A．20πB．24πC．28πD．32π15．（20XX年全国III）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为A．18+365B．54+185C．90D．8116．(20XX浙江)某几何体的三视图如图所示（单位：cm），则该几何体的体积是32340cm D．cm33317．（20XX陕西）一个几何体的三视图如图所示，则该几何体的表面积为A．8cm3B．12cm3C．A．3πB．4πC．2π+4D．3π+418．（20XX重庆）某几何体的三视图如图所示，则该几何体的体积为1212 A．+πB．+πC．+2πD．+2π333319．（20XX 新课标）一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为1111A．B．C．D．876520．（20XX 安徽）一个四面体的三视图如图所示，则该四面体的表面积是A．1+3B．2+3C．1+22D．2221．（20XX 湖南）某工件的三视图如图3所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=4(2-1)312(2-1)3816A．B．C．D．ππ9π9π22．（20XX 新课标Ⅰ）圆柱被一个平面截去一部分后与半球(半径为r )组成一个新工件的体积）原工件的体积几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16 + 20π，则r =A．1B．2C．4D．823．（20XX 新课标Ⅰ）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为A．62B．6C．42D．424．（20XX 新课标Ⅱ）如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为A．17B．5C．10D．127932725．（20XX 安徽）一个多面体的三视图如图所示，则该多面体的表面积为A．21+3B．18+3C．21D．184433326．（20XX 福建）某空间几何体的正视图是三角形，则该几何体不可能是A．圆柱B．圆锥C．四面体D．三棱柱正视图侧视图327．（20XX 浙江）某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是俯视图3A．90cm 2B．129cm 2C．132cm 2D．138cm 228．（20XX 新课标Ⅱ）正三棱柱ABC -A 1B 1C 1的底面边长为2，侧棱长为3，11-B 1DC 1的体积为D 为BC 中点，则三棱锥A 33C．1D．22229．（20XX 福建）以边长为1的正方形的一边所在直线为旋转轴，将该正方形A．3B．旋转一周所得圆柱的侧面积等于112主视图2左视图A．2πB．πC．22D．130．（20XX 辽宁）某几何体三视图如图所示，则该几何体的体积为2俯视图2431．（20XX 陕西）将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积为A．4πB．3πC．2πD．π32．（20XX 江西）一几何体的直观图如右图，下列给出的四个俯视图中正确的是A A．8-2πB．8-πC．8-πD．8-πB D俯视C333．（20XX 新课标Ⅰ）某几何体的三视图如图所示，则该几何体的体积为5226正视图121侧视图A．16+8πB．8+8πC．16+16πD．8+16π34．（20XX 江西）一几何体的三视图如右所示，则该几何体的体积为俯视图A．200+9πB．200+18πC．140+9πD．140+18π35．（20XX 广东）某几何体的三视图如图所示，它的体积为422正视图2侧视图A．12πB．45πC．57πD．81π36．（20XX 湖北）已知某几何体的三视图如图所示，则该几何体的体积为俯视图10πD．6π3A．正视图B．3πC．448π337．（2011新课标）在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为俯视图A12正视图B 侧视图CD38．（2011安徽）一个空间几何体的三视图如图所示，则该几何体的表面积为1俯视图SA．48B．32+817C．48+817D．8039．（2011辽宁）如图，四棱锥S—ABCD 的底面为正方形，SD ⊥底面ABCD，则下列结论中不正确的是．．．ADBCA．AC ⊥SB B．AB ∥平面SCDC．SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D．AB 与SC 所成的角等于DC 与SA 所成的角40．（2010安徽）一个几何体的三视图如图，该几何体的表面积为4A+版2-Applicable Achives）2三教上人（222俯视图2正视图侧视图2D．372A．280B．292C．36041．(2010浙江)若某几何体的三视图（单位：cm）如图所示，则此几何体的体4积是俯视图2352320160224D 13C．cm 3B．cm cm cm 3C 13D．3333M二、填空题A 1B 142．(20XX 天津)已知正方体ABCD -A 1B 1C 1，除面ABCD 外，该正H 1D 1的棱长为G E方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥M -EFGH F D C A．的体积为．A B 43．(20XX 江苏)如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为．44．（20XX 新课标Ⅰ）如图，圆形纸片的圆心为O ，半径为5 cm，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，∆DBC ，∆ECA ，E∆FAB 分别是以BC ，CA ，AB 为底边的等腰三角形。

重点难点
搜集整理资料；读科学家的故事；谈自己与科学结缘的经历；模仿写浅显的科学小品科学童话。

活动难点：仿写科学小品科学童话。

一课时
一．预学导航
活动准备（分组准备） 1.收集有关科学的名人名言（至少5条）?
2.讲述科学家的故事。

3.准备讲述“我第一次迷上科学”的经历。

.准备1-2篇科学小品或科学童话范文。

二．共学助行
第一阶段： 各小组竞赛：派出代表上台写出有关科学的名人名言。

（每组至少写5条，每条1分） 第二阶段： 各小组推荐一个代表讲述科学家的故事。

（讲得好的，加3分，简单的1分）第三阶段： 各小组推荐一个代表讲述 “我第一次迷上科学”的经历。

（讲得好的，加3分，一般的1分）? 第阶段： 各小组推荐一个代表范读例文，其他学生听读（得好的，加3分，一般的1分）? 根据自己迷上科学的故事和同学的启发，思考自然之谜，仿写一篇科学文。

了解现代科学技术给人类生活带来的巨大影响。

?
初中学习网，资料共分享！我们负责传递知识！。

课时作业39 空间几何体的结构特征及三视图与直观图1．如图，△A ′B ′O ′是利用斜二测画法画出的△ABO 的直观图，已知A ′B ′∥y ′轴，O ′B ′＝4，且△ABO 的面积为16，过A ′作A ′C ′⊥x ′轴，则A ′C ′的长为( A )A ．2 2B ． 2C ．16 2D ．1解析：因为A ′B ′∥y ′轴，所以△ABO 中，AB ⊥OB ． 又因为△ABO 的面积为16，所以12AB ·OB ＝16.因为OB ＝O ′B ′＝4，所以AB ＝8，所以A ′B ′＝4. 因为A ′C ′⊥O ′B ′于C ′，所以B ′C ′＝A ′C ′， 所以A ′C ′＝4·sin45°＝22，故选A ．2．如图是一几何体的直观图、正视图和俯视图，该几何体的侧视图为( B )解析：由直观图和正视图、俯视图可知，该几何体的侧视图应为面PAD，且EC投影在面PAD上且为实线，点E的投影点为PA的中点，故B正确．3．若某几何体的三视图如图所示，则这个几何体的直观图可能是( B )解析：根据正视图与俯视图可排除A，C，根据侧视图可排除D．4．(2019·某某七校联考)如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( B )A．①②⑥B．①②③C．④⑤⑥D．③④⑤解析：正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①，侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③.5．“牟合方盖”(如图1)是我国古代数学家X徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖)．其直观图如图2所示，图中四边形是为体现其直观性所作的辅助线，其实际直观图中四边形不存在，当其正视图和侧视图完全相同时，它的正视图和俯视图分别可能是( A )A ．a ，bB ．a ，cC ．c ，bD ．b ，d解析：当正视图和侧视图完全相同时，“牟合方盖”相对的两个曲面正对前方，正视图为一个圆，俯视图为一个正方形，且两条对角线为实线，故选A ．6．(2019·东北师大附中、某某市一中等五校联考)如图所示，在三棱锥D -ABC 中，已知AC ＝BC ＝CD ＝2，CD ⊥平面ABC ，∠ACB ＝90°.若其正视图、俯视图如图所示，则其侧视图的面积为( D )A ． 6B ．2C ． 3D ． 2解析：由几何体的结构特征和正视图、俯视图，得该几何体的侧视图是一个直角三角形，其中一直角边为CD ，其长度为2，另一直角边为底面△ABC 的边AB 上的中线，其长度为2，则其侧视图的面积S ＝12×2×2＝ 2.7．(2014·新课标卷Ⅰ)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( B )A．6 2 B．6C．4 2 D．4解析：由多面体的三视图可知该几何体的直观图为一个三棱锥，如图所示.其中面ABC⊥面BCD，△ABC为等腰直角三角形，AB＝BC＝4，取BC的中点M，连接AM，DM，则DM⊥面ABC，在等腰△BCD中，BD＝DC＝25，BC＝DM＝4，所以在Rt△AMD中，AD＝AM2＋DM2＝42＋22＋42＝6，又在Rt△ABC中，AC＝42＜6，故该多面体的各条棱中，最长棱为AD，长度为6，故选B．8．(2019·某某某某二中月考)一个几何体的三视图如图所示，在该几何体的各个面中，面积最小的面的面积为( D )A．8 B．4C．4 3 D．4 2解析：由三视图可知该几何体的直观图如图所示，显然S △PCD >S △ABC ，由三视图特征可知，PA ⊥平面ABC ，DB ⊥平面ABC ，AB ⊥AC ，PA ＝AB ＝AC ＝4，DB ＝2，则易得S △PAC ＝S △ABC ＝8，S 梯形ABDP＝12，S △BCD ＝12×42×2＝42，故选D ．9．(2019·某某模拟)如图，在底面边长为1，高为2的正四棱柱ABCD -A 1B 1C 1D 1中，点P是平面A 1B 1C 1D 1内一点，则三棱锥P -BCD 的正视图与侧视图的面积之和为( B )A ．1B ．2C ．3D ．4解析：设点P 在平面A 1ADD 1的射影为P ′，在平面C 1CDD 1的射影为P ″，如图所示.∴三棱锥P -BCD 的正视图与侧视图分别为△P ′AD 与△P ″CD ， 因此所求面积S ＝S △P ′AD ＋S △P ″CD ＝12×1×2＋12×1×2＝2.10．(2019·某某模拟)某四面体的三视图如图所示，该四面体的六条棱中，长度最长的棱的长是( C )A．2 5 B．2 6C．27 D．4 2解析：由三视图可知该四面体的直观图如图所示．其中AC＝2，PA＝2，△ABC中，边AC上的高为23，所以BC＝42＋232＝27，AB＝232＋22＝4，而PB＝PA2＋AB2＝22＋42＝25，PC＝PA2＋AC2＝22，因此在四面体的六条棱中，长度最长的是BC，其长为27，选C．11．一个圆台上、下底面的半径分别为3 cm和8 cm，若两底面圆心的连线长为12 cm，则这个圆台的母线长为13 cm.解析：如图，过点A作AC⊥OB，交OB于点C．在Rt△ABC中，AC＝12(cm)，BC＝8－3＝5(cm)．∴AB＝122＋52＝13(cm)．12．(2019·某某模拟)正四棱锥的底面边长为2，侧棱长均为3，其正视图和侧视图是全等的等腰三角形，则正视图的周长为2＋2 2.解析：由题意知，正视图就是如图所示的截面PEF，其中E，F分别是AD，BC的中点，连接AO，易得AO＝2，又PA＝3，于是解得PO＝1，所以PE＝2，故其正视图的周长为2＋2 2.13．(2019·某某模拟)一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A出发，经正方体的表面，按最短路线爬行到顶点C1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( D )A．①②B．①③C．③④D．②④解析：由点A经正方体的表面，按最短路线爬行到达顶点C1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB1A1和平面BCC1B1展开到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过BB1的中点，此时对应的正视图为②；若把平面ABCD和平面CDD1C1展开到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过CD的中点，此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现．故选D．14．已知以下三视图中有三个同时表示某一个棱锥，则下列不是该三棱锥的三视图的是( D )解析：四个选项中，因为观察的位置不同，得到的三个视图也不同．可从俯视图入手，以A选项中的正方向作为标准．则A中的方向如图所示．B 中的方向C 中的方向15．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积是283.解析：可从俯视图入手，观察得知，可能是三棱台，再观察侧视图和正视图验证想法．可得该多面体为棱锥S -A 1B 1C 1由平面ABC 截得的棱台．AB ＝AC ＝2，A 1B 1＝A 1C 1＝4，所以SA 1＝4，VS -A 1B 1C 1＝323，V S -ABC ＝43，所以VABC -A 1B 1C 1＝283.word16．某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy的最大值为64.解析：由三视图知三棱锥如图所示，底面ABC是直角三角形，AB⊥BC，PA⊥平面ABC，BC＝27，PA2＋y2＝102，(27)2＋PA2＝x2，因此xy＝x102－[x2－272]＝x128－x2≤x2＋128－x22＝64，当且仅当x2＝128－x2，即x＝8时取等号，因此xy的最大值是64.。

空间几何体（1）认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构.（2）能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述三视图所表示的立体模型，会用斜二测法画出它们的直观图.（3）会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式.（4）会画某些建筑物的视图与直观图（在不影响图形特征的基础上，尺寸、线条等不作严格要求）.一、空间几何体的结构1．多面体①底面互相平行.②侧面都是平行四边形.③每相邻两个平行四边形的公共边互相平行.2之间满足关系式1．空间几何体的三视图（1）三视图的概念①光线从几何体的前面向后面正投影，得到的投影图叫做几何体的正视图;②光线从几何体的左面向右面正投影，得到的投影图叫做几何体的侧视图;③光线从几何体的上面向下面正投影，得到的投影图叫做几何体的俯视图.几何体的正视图、侧视图和俯视图统称为几何体的三视图.如图.（2）三视图的画法规则①排列规则：一般地，侧视图在正视图的右边，俯视图在正视图的下边.如下图：②画法规则ⅰ)正视图与俯视图的长度一致，即“长对正”；ⅱ)侧视图和正视图的高度一致，即“高平齐”；ⅲ)俯视图与侧视图的宽度一致，即“宽相等”.③线条的规则ⅰ)能看见的轮廓线用实线表示；ⅱ)不能看见的轮廓线用虚线表示.（3）常见几何体的三视图（1）斜二测画法及其规则对于平面多边形，我们常用斜二测画法画它们的直观图.斜二测画法是一种特殊的画直观图的方法，其画法规则是：①在已知图形中取互相垂直的轴和y轴，两轴相交于点O.画直观图时，把它们画成对应的′轴和y′轴，两轴相交于点O′，且使∠′O′y′=45°(或135°)，它们确定的平面表示水平面.②已知图形中平行于轴或y轴的线段，在直观图中分别画成平行于′轴或y′轴的线段.③已知图形中平行于轴的线段，在直观图中保持原长度不变，平行于y轴的线段，长度为原的一半.（2）用斜二测画法画空间几何体的直观图的步骤①在已知图形所在的空间中取水平平面，作互相垂直的轴O，Oy，再作O轴使∠O=90°，且∠yO=90°.②画直观图时，把它们画成对应的轴O′′，O′y′，O′′，使∠′O′y′=45°(或135°)，∠′O′′=90°，′O′y′所确定的平面表示水平平面.③已知图形中，平行于轴、y轴或轴的线段，在直观图中分别画成平行于′轴、y′轴或′轴的线段，并使它们和所画坐标轴的位置关系与已知图形中相应线段和原坐标轴的位置关系相同.④已知图形中平行于轴或轴的线段，在直观图中保持长度不变，平行于y轴的线段，长度变为原的一半.⑤画图完成以后，擦去作为辅助线的坐标轴，就得到了空间图形的直观图.（3）直观图的面积与原图面积之间的关系①原图形与直观图的面积比为，即原图面积是直观图面积的倍，②直观图面积是原图面积的倍.考向一空间几何体的结构特征关于空间几何体的结构特征问题的注意事项：(1)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型，在条件不变的情况下，变换模型中的线面关系或增加线、面等基本元素，然后再依据题意判定．(2)通过举反例对结构特征进行辨析，即要说明一个命题是错误的，只要举出一个反例即可.典例1 给出下列四个命题：①各侧面都是全等四边形的棱柱一定是正棱柱；②对角面是全等矩形的六面体一定是长方体；③若棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥；④长方体一定是正四棱柱.其中正确的命题个数是A．0 B．1C．2 D．3【答案】A1．正三棱锥内有一个内切球,经过棱锥的一条侧棱和高作截面,正确的图是典例2 边长为5 cm的正方形EFGH是圆柱的轴截面，则从E点沿圆柱的侧面到相对顶点G的最短距离是A．10 cm B．cmC．cm D．cm【答案】D【名师点睛】求几何体的侧面上两点间的最短距离问题，常常把侧面展开，转化为平面几何问题处理．2．已知正三棱柱的底面边长为1,侧棱长为2,为的中点,则从拉一条绳子绕过侧棱到达点的最短绳长为A．B．C．D．考向二空间几何体的三视图三视图问题的常见类型及解题策略：(1)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．(2)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线，不能看到的部分用虚线表示．(3)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合.典例3 如图所示，在放置的四个几何体中，其正视图为矩形的是A B C D 【答案】B【解析】A选项三棱锥、C选项圆台、D选项的正视图都不是矩形，而B选项圆柱的正视图为矩形.故选B．3．如图，在正方体中，分别为棱的中点，用过点的平面截去该正方体的上半部分，则剩余几何体（下半部分）的侧视图为典例4 如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是A．三棱锥B．三棱柱C．四棱锥D．四棱柱【答案】B4．某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的最大值为A．B．C． D．考向三空间几何体的直观图斜二测画法中的“三变”与“三不变”：“三变”；“三不变”.典例5 如图是水平放置的平面图形的直观图,则原平面图形的面积为A．3 B．C．6 D．【答案】C【方法点晴】本题主要考查了平面图形的直观图及其原图形与直观图面积之间的关系，属于基础题，解答的关键是牢记原图形与直观图的面积比为，即原图面积是直观图面积的倍，直观图面积是原图面积的倍.5．已知梯形是直角梯形，按照斜二测画法画出它的直观图（如图所示），其中，，，则直角梯形边的长度是A．B．C．D．1．有下列三个说法：①用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台；②有两个面平行且相似，其余各面都是梯形的多面体是棱台；③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台．其中正确的有A．0个B．1个C．2个 D．3个2．将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的正视图为A B C D 3．某空间几何体的正视图是三角形，则该几何体不可能是A．圆柱B．圆锥C．四面体D．三棱柱4．某正四棱锥的正（主）视图和俯视图如图所示，则该正四棱锥的侧棱长是A．B．C．D．5．用斜二测画法画一个水平放置的平面图形的直观图是如图所示的一个正方形，则原的图形是A．B．C．D．6．一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为①长方形；②正方形；③圆；④椭圆中的A．①②B．②③C．③④D．①④7．一个四面体的顶点在空间直角坐标系中的坐标分别是，绘制该四面体的三视图时，按照如下图所示的方向画正视图，则得到的正视图为A．B．C．D．8．已知用一个平行于棱锥底面的平面截这个棱锥，截得的棱台上、下底面面积比为1∶4，截去的棱锥的高是，则棱台的高是A． B．C． D．9．一个正方体的内切球、外接球、与各棱都相切的球的半径之比为A．B．C．D．10．如图，网格纸上小正方形的边长为1，粗实线和虚线画出的是某几何体的三视图，该几何体的各个面中有若干个是梯形，则这些梯形的面积之和为A．28 B．30C．32 D．3611．长方体中，，，设点关于直线的对称点为，则与两点之间的距离是A． B．C．D．12．某三棱锥的三视图如图所示，则该三棱锥的最长棱的长度为A．B．C．D．13．如图所示,E,F分别为正方体ABCD-A'B'C'D'的面ADD'A'、面BCC'B'的中心,现给出图①~④的4个平面图形,则四边形BFD'E在该正方体的面上的射影可能是图.(填上所有正确图形对应的序号)14．如图所示是一个几何体的表面展开平面图,该几何体中与“数”字面相对的是“”.15．已知某一几何体的正视图与侧视图如图所示，则下列图形中，可以是该几何体的俯视图的图形有_____________.（填序号）16．一个水平放置的平面图形的斜二测直观图是一个底角为，腰和上底均为1的等腰梯形，则这个平面图形的面积为____________.17．正三棱锥P−ABC中，，，AB的中点为M，一小蜜蜂沿锥体侧面由M爬到C点，最短路程是____________.1．（2018新课标全国Ⅰ理科）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为A．B．C．3 D．22．（2018新课标全国Ⅲ理科）中国古建筑借助榫卯将木构件连接起，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是3．（2017新课标全国Ⅰ理科）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12C．14 D．164．（2017北京理科）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为A．3B．2C．2D．21．【答案】C【解析】正三棱锥的内切球与各个面的切点为正三棱锥各面的中心,所以过一条侧棱和高的截面必过该棱所对的面的高线,故C正确.4．【答案】B【解析】由已知中的三视图可得该几何体是一个以侧视图为底面的直四棱柱，在该几何体的所有顶点中任取两个顶点，它们之间距离取最大值时，最大距离相当于一个长、宽、高分别为2，1，1的长方体的体对角线，为=，故选B．5．【答案】B【解析】根据斜二测画法，原的高变成了方向的线段，且长度是原高的一半，则原高为，而横向长度不变，且梯形是直角梯形，如图，，故选B.1．【答案】A【解析】本题主要考查棱台的结构特征．①中的平面不一定平行于底面，故①错；②③可用反例去检验，如图所示，故②③错．2．【答案】D【解析】所得几何体的正视图为一个长方形，且有一条从左下到右上的对角线，如下所示：故选D．5．【答案】A【解析】根据斜二测画法知，平行于轴的线段长度不变,平行于y的线段变为原的，由此得原的图形是A．故选A．6．【答案】B【解析】若俯视图为正方形，则正视图中的边长不成立；若俯视图为圆，则正视图中的边长也不成立．所以其俯视图不可能为②正方形；③圆，故选B．7．【答案】D【解析】根据空间直角坐标系中点的位置，画出直观图如图，则正视图为D中图形.故选D．【方法点睛】球与几何体的组合体的问题，尤其是相切，一般不画组合体的直观图，而是画切面图，圆心到切点的距离是半径并且垂直，如果是内切球，那么对面切点的距离就是直径，而对面切点的距离是棱长，如果与棱相切，那么对棱切点的距离就是直径，而切点在棱的中点，所以对棱中点的距离等于面对角线长，而如果外接球，那么相对顶点的距离就是直径，即正方体的体对角线是直径．10．【答案】C【解析】由三视图可知该几何体如图所示，各个面中有两个梯形，一个矩形，两个直角三角形，则这两个梯形的面积和为.故选C．11．【答案】A12．【答案】C【解析】由三视图可知：原三棱锥为，其中，，如图，∴这个三棱锥最长棱的棱长是.故选C．13．【答案】②③【解析】四边形BFD'E在正方体ABCD-A'B'C'D'的面BCC'B'上的射影是③;在面ABCD上的射影是②;易知①④的情况不可能出现.14．【答案】学【解析】由图形可知,该几何体为三棱台，两个三角形为三棱台的上下底面，∴与“数”字面相对的是“学”.15．【答案】①②③④16．【答案】【解析】由题意得，水平放置的平面图形的斜二测直观图是一个底角为，腰和上底均为1的等腰梯形，其面积为，又原图形与直观图的面积比为，所以原图形的面积为．17．【答案】【解析】由题意，将侧面PBC展开，那么点M到C的距离，就是在中的长度，由题中数据易得，，，如果将侧面PAC展开，同理可得.1．【答案】B【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题，在解题的过程中，需要明确两个点在几何体上所处的位置，再利用平面上两点间直线段最短，所以处理方法就是将面切开平铺，利用平面图形的相关特征求得结果.2．【答案】A【解析】本题主要考查空间几何体的三视图.由题意知，俯视图中应有一不可见的长方形，且俯视图应为对称图形.故选A．3．【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为，故选B．【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.4．【答案】B【解析】几何体是四棱锥，如图.最长的棱长为补成的正方体的体对角线，即该四棱锥的最长棱的长度为，故选B．【名师点睛】本题考查了空间想象能力，由三视图还原几何体的方法或者也可根据三视图的形状，将几何体的顶点放在正方体或长方体里面，便于分析问题.。

空间几何体的表面积和体积培优班专题资料考点一 几何体的表面积(1)一个正方体的棱长为m ，表面积为n ，一个球的半径为p ，表面积为q .若m p ＝2，则n q＝( ) A.8πB.6πC.π6D.π8解析 由题意可以得到n ＝6m 2，q ＝4πp 2，所以n q ＝6m 24πp 2＝32π×4＝6πB. 答案 B(2)某一几何体的三视图如图所示，则该几何体的表面积为( )A ．54B ．58C ．60D ．63解析 由三视图可知，该几何体是一个棱长为3的正方体截去一个长、宽、高分别为1，1，3的长方体，所以该几何体的表面积S 表＝6×32＋2×1×3＝60. 答案 C(3)(2015·陕西，5)一个几何体的三视图如图所示，则该几何体的表面积为A ．3πB ．4πC ．2π＋4D ．3π＋4解析 由三视图可知原几何体为半圆柱，底面半径为1，高为2，则表面积为：S ＝2×12π×12＋12×2π×1×2＋2×2＝π＋2π＋4＝3π＋4. 答案 D(4)(2015·安徽，7)一个四面体的三视图如图所示，则该四面体的表面积是( )A ．1＋ 3B ．2＋ 3C ．1＋2 2D ．2 2解析 由空间几何体的三视图可得该空间几何体的直观图，如图，∴该四面体的表面积为S 表＝2×12×2×1＋2×34×(2)2＝2＋3，故选B. 答案 B(5)(2015·新课标全国Ⅱ，9)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点，若三棱锥O －ABC 体积的最大值为36，则球O 的表面积为( ) A ．36πB ．64πC ．144πD ．256π解析 如图，要使三棱锥O －ABC 即C －OAB 的体积最大，当且仅当点C 到平面OAB 的距离，即三棱锥C －OAB 底面OAB 上的高最大，其最大值为球O 的半径R ，则V O －ABC 最大＝V C －OAB 最大＝13×12S △OAB ×R ＝13×12×R 2×R ＝16R 3＝36，所以R ＝6，得S 球O ＝4πR 2＝4π×62＝144π，选C. 答案 C(6)(2014·重庆，7)某几何体的三视图如图所示，则该几何体的表面积为( )A ．54B ．60C ．66D ．72解析 该几何体的直观图如图所示，易知该几何体的表面是由两个直角三角形，两个直角梯形和一个矩形组成的，则其表面积S ＝12×3×4＋12×3×5＋2＋52×5＋2＋52×4＋3×5＝60.选B.答案 B(7)(2014·浙江，3)某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是( )A ．90 cm 2B ．129 cm 2C ．132 cm 2D ．138 cm 2解析 由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图)，其表面积为S ＝3×5＋2×12×4×3＋4×3＋3×3＋2×4×3＋2×4×6＋3×6＝138(cm 2)．答案 D(8)(2014·大纲全国，8)正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为( ) A.81π4B ．16πC ．9πD.27π4解析 设球的半径为R ，由题意可得(4－R )2＋(2)2＝R 2，解得R ＝94，所以该球的表面积为4πR 2＝81π4.故选A.(9)(2014·安徽，7)一个多面体的三视图如图所示，则该多面体的表面积为( )A ．21＋ 3B ．18＋3C ．21D ．18解析 根据题意作出直观图如图，该多面体是由正方体切去两个角而得到的，根据三视图可知其表面积为6(22－12×1×1)＋2×34×(2)2＝6×72＋3＝21＋ 3.故选A.答案 A(10)(2012·安徽，12)某几何体的三视图如图所示，该几何体的表面积是________．解析 由三视图可知，该几何体为底面是直角梯形且侧棱垂直于底面的棱柱，故该几何体的表面积为S＝2×12×(2＋5)×4＋[2＋5＋4＋42＋（5－2）2]×4＝92.答案 92考点二 几何体的体积(1)某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x 的值是( )A ．2 B.92 C.32D ．3解析 根据三视图判断几何体为四棱锥，其直观图是：V ＝13×1＋22×2x ＝3⇒x ＝3. 故选D. 答案 D(2)(2015·山东，7)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3B.4π3C.5π3D ．2π解析 如图，由题意，得BC ＝2，AD ＝AB ＝1.绕AD 所在直线旋转一周后所得几何体为一个圆柱挖去一个圆锥的组合体．所求体积V ＝π×12×2－13π×12×1＝53π.答案 C(3)(2015·重庆，5)某几何体的三视图如图所示，则该几何体的体积为( )A.13＋π B.23＋π C.13＋2π D.23＋2π解析 这是一个三棱锥与半个圆柱的组合体，V ＝12π×12×2＋13⎝⎛⎭⎫12×1×2×1＝π＋13，选A.答案 A (4)(2015·新课标全国Ⅱ，6)一个正方体被一个平面截去一部分后，剩余部分的三视图如图所示，则截去部分体积与剩余部分体积的比值为()A.18B.17C.16D.15解析 如图，由题意知，该几何体是正方体ABCD －A 1B 1C 1D 1被过三点A 、B 1、D 1的平面所截剩余部分，截去的部分为三棱锥A －A 1B 1D 1，设正方体的棱长为1，则截去部分体积与剩余部分体积的比值为111111A A B D B C D ABCDV V --＝1111111111A AB D A BCD ABCD A A B D V V V ----＝13×12×12×113－13×12×12×1＝15，选D.答案 D(5)某几何体的三视图如图所示，它的体积为()A ．72πB ．48πC ．30πD ．24π解析 由三视图可知，该几何体是半个球体和一个倒立圆锥体的组合体，球的半径为3，圆锥的底面半径为3，高为4，则根据体积公式可得几何体的体积为30π，故选C.答案 C(6)(2014·陕西，5)已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为( ) A.32π3B ．4πC ．2πD.4π3解析 如图为正四棱柱AC 1.根据题意得AC ＝2，∴对角面ACC 1A 1为正方形，∴外接球直径2R ＝A 1C ＝2，∴R ＝1，∴V 球＝4π3，故选D.答案 D(7)(2014·湖北，8)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也．又以高乘之，三十六成一．该术相当于给出了由圆锥的底面周长L 与高h ，计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式V ≈275L 2h 相当于将圆锥体积公式中的π近似取为( ) A.227B.258C.15750D.355113解析 圆锥的体积V ＝13πr 2h ＝13π⎝⎛⎭⎫L 2π2h ＝L 2h 12π，由题意得12π≈752，π近似取为258，故选B.答案 B(8)(2014·新课标全国Ⅱ，6)如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析 由三视图知该零件是两个圆柱的组合体．一个圆柱的底面半径为2 cm ，高为4 cm ；另一个圆柱的底面半径为3 cm ，高为2 cm.则零件的体积V 1＝π×22×4＋π×32×2＝34π(cm 3)．而毛坯的体积V ＝π×32×6＝54π(cm 3)，因此切削掉部分的体积V 2＝V －V 1＝54π－34π＝20π(cm 3)，所以V 2V ＝20π54π＝1027.故选C.答案 C (9)(2012·新课标全国，11)已知三棱锥S ­ABC 的所有顶点都在球O 的球面上， △ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( ) A.26B.36C.23D.22解析 如图，H 为△ABC 的外接圆圆心，则∠BHC ＝120°，设△ABC 的外接圆半径为r ，则1＝BC 2＝HC 2＋HB 2－2HC ·HB ·cos 120°＝3r 2， ∴r ＝33. 连接OH ，根据球的截面性质知，OH ⊥平面ABC ，∴OH ＝OC 2－CH 2＝1－13＝63∵O 为SC 的中点，∴S 到平面ABC 的距离为2OH ＝263，∴V S ­ABC ＝13S △ABC ×263＝13×34×263＝26.答案 A(10)(2015·江苏，9)现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为________．解析 设新的底面半径为r ，由题意得13πr 2·4＋πr 2·8＝13π×52×4＋π×22×8，解得r ＝7.答案7(11)(2014·江苏，8)设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2，若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是________．解析 设圆柱甲的底面半径为r 1，高为h 1，圆柱乙的底面半径为r 2，高为h 2.由题意得S 1S 2＝πr 21πr 22＝94，∴r 1r 2＝32. 又∵S 甲侧＝S 乙侧，即2πr 1h 1＝2πr 2h 2，∴h 1h 2＝r 2r 1＝23， 故V 1V 2＝S 1h 1S 2h 2＝S 1S 2·h 1h 2＝94×23＝32答案 32(12)(2013·江苏，8)如图，在三棱柱A 1B 1C 1­ABC 中，D ，E ，F 分别是AB ，AC ，AA 1的中点，设三棱锥F ­ADE 的体积为V 1，三棱柱A 1B 1C 1­ABC 的体积为V 2，则V 1∶V 2＝________.解析 由题意可知点F 到面ABC 的距离与点A 1到面ABC 的距离之比为1∶2，S △ADE ∶S △ABC ＝1∶4. 因此V 1∶V 2＝13AF ·S △AED 2AF ·S △ABC＝1∶24.答案 1∶24。

第1讲空间几何体的结构特征及三视图和直观图1．(2024·沈阳市教学质量监测(一))“牟合方盖”是我国古代数学家刘徽在探讨球的体积的过程中构造的一个和谐美丽的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好像两个扣合(牟合)在一起的方形伞(方盖)．其直观图如图，图中四边形是为体现其直观性所作的协助线．当其正视图和侧视图完全相同时，它的俯视图可能是( )解析：选B.依据直观图以及图中的协助四边形分析可知，当正视图和侧视图完全相同时，俯视图为B，故选B.2．已知某空间几何体的俯视图如图所示，则此几何体的正视图不行能为( )解析：选D.选项A，可想象为三个圆柱叠放在一起；选项B，可想象为三个球叠放在一起；选项C，可想象为一个圆台和一个圆柱叠放在一起；选项D，可想象为上面为一个小圆柱，下面为一个空心球，则其俯视图中的中间圆应为虚线．故选D.3．将长方体截去一个四棱锥后得到的几何体如图所示，则该几何体的侧视图为( )解析：选D.依据几何体的结构特征进行分析即可．4．若某几何体的三视图如图所示，则这个几何体的直观图可以是( )解析：选D.A ，B 的正视图不符合要求，C 的俯视图明显不符合要求，故选D. 5．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的正视图(等腰直角三角形)和侧视图，且该几何体的体积为83，则该几何体的俯视图可以是( )解析：选C.由正视图和侧视图及体积易得几何体是四棱锥P ­ABCD ，其中ABCD 是边长为2的正方形，PA ⊥平面ABCD ，且PA ＝2，此时V P ­ABCD ＝13×22×2＝83，则俯视图为Rt △PAB ，故选C.6.如图，一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则该平面图形的面积为________．解析：直观图的面积S′＝12×(1＋1＋2)×22＝2＋12.故原平面图形的面积S＝S′24＝2＋ 2.答案： 2＋ 27．一个圆台上、下底面的半径分别为3 cm和8 cm，若两底面圆心的连线长为12 cm，则这个圆台的母线长为________cm.解析：如图，过点A作AC⊥OB，交OB于点C.在Rt△ABC中，AC＝12 cm，BC＝8－3＝5(cm)．所以AB＝122＋52＝13(cm)．答案：138．已知正四棱锥V­ABCD中，底面面积为16，一条侧棱的长为211，则该棱锥的高为________．解析：如图，取正方形ABCD的中心O，连接VO，AO，则VO就是正四棱锥V­ABCD的高．因为底面面积为16，所以AO＝2 2.因为一条侧棱长为211，所以VO＝VA2­AO2＝44－8＝6.所以正四棱锥V­ABCD的高为6.答案：69．某几何体的三视图如图所示．(1)推断该几何体是什么几何体？(2)画出该几何体的直观图．解：(1)该几何体是一个正方体切掉两个14圆柱后得到的几何体．(2)直观图如图所示．10．如图所示的三个图中，上面是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图如图所示(单位：cm)．(1)在正视图下面，依据画三视图的要求画出该多面体的俯视图； (2)依据给出的尺寸，求该多面体的体积．解：(1)如图．(2)所求多面体的体积V ＝V 长方体－V 正三棱锥＝4×4×6－13×(12×2×2)×2＝2843(cm 3)．1．已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边长为2的直角三角形，则该三棱锥的正视图可能为( )解析：选C.当正视图为等腰三角形时，则高应为2，且应为虚线，解除A ，D ；当正视图是直角三角形，由条件得一个直观图如图所示，中间的线是看不见的线PA 形成的投影，应为虚线，故答案为C.2．(2024·兰州适应性考试)如图，在正方体ABCD ­A 1B 1C 1D 1中，点P 是线段A 1C 1上的动点，则三棱锥P ­BCD 的俯视图与正视图面积之比的最大值为( )A ．1 B. 2 C. 3D ．2解析：选D.正视图，底面B ，C ，D 三点，其中D 与C 重合，随着点P 的改变，其正视图均是三角形且点P 在正视图中的位置在边B 1C 1上移动，由此可知，设正方体的棱长为a ，则S正视图＝12×a 2；设A 1C 1的中点为O ，随着点P 的移动，在俯视图中，易知当点P 在OC 1上移动时，S 俯视图就是底面三角形BCD 的面积，当点P 在OA 1上移动时，点P 越靠近A 1，俯视图的面积越大，当到达A 1的位置时，俯视图为正方形，此时俯视图的面积最大，S俯视图＝a 2，所以S 俯视图S 正视图的最大值为a 212a2＝2，故选D.3．(2024·合肥其次次质量检测)如图，在正方体ABCD­A1B1C1D1中，E是棱A1B1的中点，用过点A，C，E的平面截正方体，则位于截面以下部分的几何体的侧(左)视图为( )解析：选A.如图，取B1C1的中点为F，连接AC，CF，EF，AE，截面AEFC以下部分为所求得的几何体，易知选项A中的图形为其侧视图，故选A.4．如图是一个几何体的三视图，则该几何体随意两个顶点间距离的最大值是________．解析：作出直观图如图所示，通过计算可知AF、DC最长且DC＝AF＝BF2＋AB2＝3 3.答案：3 35．如图，在四棱锥P­ABCD中，底面为正方形，PC与底面ABCD垂直，如图为该四棱锥的正视图和侧视图，它们是腰长为6 cm的全等的等腰直角三角形．(1)依据图中所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；(2)求PA.解：(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形，如图，其面积为36 cm2.俯视图(2)由侧视图可求得PD＝PC2＋CD2＝62＋62＝6 2 (cm)．由正视图可知AD＝6 cm，且AD⊥PD，所以在Rt△APD中，PA＝PD2＋AD2＝（62）2＋62＝6 3 (cm)．6．已知正三棱锥V­ABC的正视图和俯视图如图所示．(1)画出该三棱锥的直观图和侧视图．(2)求出侧视图的面积．解：(1)如图．(2)侧视图中VA ＝42－⎝ ⎛⎭⎪⎫23×32×232＝12＝2 3.则S △VBC ＝12×23×23＝6.。

湘艺版音乐二年级下册第6课《加伏特舞曲》教学设计一. 教材分析《加伏特舞曲》是湘艺版音乐二年级下册第6课的一首曲目，这是一首富有节奏感和生动形象的舞曲。

通过学习这首舞曲，学生可以了解加伏特舞曲的基本特点，感受三拍子的强弱规律，培养学生的音乐欣赏能力和舞蹈表现力。

二. 学情分析二年级的学生已经具备了一定的音乐基础，对简单的节奏和旋律有一定的感知能力。

但学生在音乐欣赏和舞蹈表现方面还存在一定的局限性，需要通过教师的引导和教学活动来提高。

三. 教学目标1.让学生了解加伏特舞曲的基本特点，感受三拍子的强弱规律。

2.培养学生对音乐的理解和欣赏能力，提高舞蹈表现力。

3.培养学生积极参与音乐活动的兴趣，增进同学间的合作与交流。

四. 教学重难点1.加伏特舞曲的特点和三拍子的强弱规律。

2.引导学生理解音乐与舞蹈的结合，提高舞蹈表现力。

五. 教学方法1.欣赏法：通过聆听和欣赏优秀的加伏特舞曲作品，让学生感受舞曲的特点和魅力。

2.讲解法：教师讲解加伏特舞曲的基本特点和三拍子的强弱规律，帮助学生理解和学习。

3.实践法：引导学生参与舞蹈实践活动，提高学生的舞蹈表现力。

4.合作法：鼓励学生之间相互合作，共同完成舞蹈作品。

六. 教学准备1.教学课件：制作相关的教学课件，展示加伏特舞曲的特点和魅力。

2.音响设备：准备音响设备，播放加伏特舞曲作品。

3.舞蹈道具：准备简单的舞蹈道具，如手绢、扇子等。

七. 教学过程1.导入（5分钟）教师通过播放一首加伏特舞曲作品，引导学生进入音乐课堂。

简要介绍加伏特舞曲的基本特点和三拍子的强弱规律。

2.呈现（10分钟）教师展示舞蹈道具，如手绢、扇子等，引导学生欣赏舞蹈的美感。

讲解舞蹈与音乐的结合，让学生理解舞蹈是在音乐的伴奏下进行的。

3.操练（10分钟）教师带领学生一起学习舞蹈动作，如跳跃、旋转等。

注意引导学生感受三拍子的强弱规律，培养学生的舞蹈节奏感。

4.巩固（5分钟）学生分组进行舞蹈练习，相互观摩和交流，巩固所学舞蹈动作。

升级增分训练立体几何1．某四面体的三视图如图，则其四个面中最大的面积是()A．2B．2 2C． 3 D．2 3解析：选D在正方体ABCD-A1B1C1D1中还原出三视图的直观图，其是一个三个顶点在正方体的右侧面、一个顶点在左侧面的三棱锥，即为D1-BCB1，如图所示，其四个面的面积分别为2,22，22，23，故选D．2．(2019·广东茂名二模)若几何体的三视图如图所示，则该几何体的外接球的表面积为()A．34π B．35πC．36π D．17π解析：选A由几何体的三视图知它是底面为正方形且有一条侧棱垂直于底面的四棱锥，可把它补成一个长、宽、高分别为3,3,4的长方体，该长方体的外接球即为原四棱锥的外接球，所以4R2＝32＋32＋42＝34(其中R为外接球的半径)，外接球表面积为S＝4πR2＝34π．3．(2019·湖南长沙三校联考)已知点E，F，G分别是正方体ABCD-A1B1C1D1的棱AA1，CC1，DD1的中点，点M，N，Q，P分别在线段DF，AG，BE，C1B1上．以M，N，Q，P为顶点的三棱锥P-MNQ的俯视图不可能是()解析：选C 当M 与F 重合、N 与G 重合、Q 与E 重合、P 与B 1重合时，三棱锥P -MNQ 的俯视图为A ；当M ，N ，Q ，P 是所在线段的中点时，三棱锥P -MNQ 的俯视图为B ；当M ，N ，Q ，P 位于所在线段的非端点位置时，存在三棱锥P -MNQ ，使其俯视图为D ．4．(2019·河南中原名校联考)如图，四棱柱ABCD -A 1B 1C 1D 1是棱长为1的正方体，四棱锥S -ABCD 是高为1的正四棱锥，若点S ，A 1，B 1，C 1，D 1在同一个球面上，则该球的表面积为( )A ．916πB ．2516πC ．4916πD ．8116π解析：选D 作如图所示的辅助线，其中O 为球心，设OG 1＝x ，则OB 1＝SO ＝2－x ，由正方体的性质知B 1G 1＝22，则在Rt △OB 1G 1中，OB 21＝G 1B 21＋OG 21，即(2－x )2＝x 2＋⎝ ⎛⎭⎪⎫222， 解得x ＝78，所以球的半径R ＝OB 1＝98，所以球的表面积为S ＝4πR 2＝8116π．5．(2019·湖南长沙四校一模)某几何体的三视图如图所示，则该几何体的体积为( )A ．1136B ． 3C ．533D ．433解析：选B 由三视图知该几何体是一个四棱锥，其直观图如图所示，△P AD 为正三角形，四棱锥的底面是直角梯形，四棱锥的高为3，∴所求体积V ＝13×⎣⎢⎡⎦⎥⎤12×(1＋2)×2×3＝3．6．(2019·湖南郴州模拟)一只蚂蚁从正方体ABCD -A 1B 1C 1D 1的顶点A 出发，经正方体的表面，按最短路线爬行到顶点C 1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )A ．①②B ．①③C ．③④D ．②④解析：选D 由点A 经正方体的表面，按最短路线爬行到达顶点C 1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB 1A 1和平面BCC 1B 1展到同一个平面内，连接AC 1，则AC 1是最短路线，且AC 1会经过BB 1的中点，此时对应的正视图为②；若把平面ABCD 和平面CDD 1C 1展到同一个平面内，连接AC 1，则AC 1是最短路线，且AC 1会经过CD 的中点，此时对应的正视图为④．而其他几种展开方式对应的正视图在题中没有出现．7．(2019·福建省质检)在三棱锥P -ABC 中，P A ＝23，PC ＝2，AB ＝7，BC ＝3，∠ABC ＝π2，则三棱锥P -ABC 外接球的表面积为( )A ．4πB ．163πC ．323πD ．16π解析：选D 设三棱锥P -ABC 的外接球的半径为R ，在△ABC 中，因为AB ＝7，BC ＝3，∠ABC ＝π2，所以AC ＝AB 2＋BC 2＝4．在△P AC 中，因为P A ＝23，PC＝2，AC ＝4，所以P A 2＋PC 2＝AC 2，所以∠APC ＝π2，所以AC 为三棱锥P -ABC 的外接球的直径，所以R ＝2，所以此三棱锥的外接球的表面积S ＝4πR 2＝4π×22＝16π．8．(2019·南宁模拟)设点A ，B ，C 为球O 的球面上三点，O 为球心．球O 的表面积为100π，且△ABC 是边长为43的正三角形，则三棱锥O -ABC 的体积为( )A ．12B ．12 3C ．24 3D ．36 3解析：选B ∵球O 的表面积为100π＝4πr 2，∴球O 的半径为5．如图，取△ABC 的中心H ，连接OH ，连接并延长AH交BC 于点M ，则AM ＝(43)2－⎝ ⎛⎭⎪⎫4322＝6，AH ＝23AM ＝4，∴OH ＝OA 2－AH 2＝52－42＝3，∴三棱锥O -ABC 的体积为V ＝13×34×(43)2×3＝123．9．如图，三棱锥V -ABC 的底面为正三角形，侧面VAC 与底面垂直且VA ＝VC ，已知其正视图的面积为23，则其侧视图的面积为________． 解析：设三棱锥V -ABC 的底面边长为a ，侧面VAC 的边AC 上的高为h ，则ah ＝43，其侧视图是由底面三角形ABC 边AC 上的高与侧面三角形VAC 边AC 上的高组成的直角三角形，其面积为12×32a×h＝12×32×43＝33．答案：3 310．(2019·南昌一模)正三角形ABC的边长为2，将它沿高AD翻折，使点B与点C间的距离为2，此时四面体ABCD外接球的表面积为________．解析：由题知，求四面体ABCD的外接球的表面积可转化为求长、宽、高分别为1,1，3的长方体的外接球的表面积，其半径R＝1212＋12＋(3)2＝52，所以S＝4πR2＝5π．答案：5π11．(2019·江西师大附中模拟)已知边长为23的菱形ABCD中，∠BAD＝60°，沿对角线BD折成二面角A-BD-C的大小为120°的四面体，则四面体的外接球的表面积为________．解析：如图1，取BD的中点E，连接AE，CE．由已知条件可知，平面ACE ⊥平面BCD．易知外接球球心在平面ACE内，如图2，在CE上取点G，使CG＝2GE，过点G作l1垂直于CE，过点E作l2垂直于AC，设l1与l2交于点O，连接OA，OC，则OA＝OC，易知O即为球心．分别解△OCG，△EGO可得R＝OC＝7，∴外接球的表面积为28π．答案：28π12．(2019·贵州适应性考试)已知正三棱柱(底面是正三角形，侧棱与底面垂直)的体积为3 3 cm3，其所有顶点都在球O的球面上，则球O的表面积的最小值为________cm2．解析：球O的表面积最小等价于球O的半径R最小．设正三棱柱的底面边长为a，高为b，则正三棱柱的体积V＝34a2b＝33，所以a2b＝12．底面正三角形所在截面圆的半径r＝33a，则R2＝r2＋⎝⎛⎭⎪⎫b22＝⎝⎛⎭⎪⎫33a2＋b24＝13×12b＋b24＝4b＋b24，令f(b)12999数学网＝4b ＋b 24，0＜b ＜2R ，则f ′(b )＝b 3－82b 2．令f ′(b )＝0，解得b ＝2，当0＜b ＜2时f ′(b )＜0，函数f (b )单调递减，当b ＞2时，f ′(b )＞0，函数f (b )单调递增，所以当b ＝2时，f (b )取得最小值3，即(R 2)min ＝3，故球O 的表面积的最小值为4π(R 2)min ＝12π．答案：12π13．如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到△A 1BE 的位置，如图2．(1)证明：CD ⊥平面A 1OC ；(2)若平面A 1BE ⊥平面BCDE ，求平面A 1BC 与平面A 1CD 的夹角的余弦值． 解：(1)证明：在题图1中，因为AB ＝BC ＝1，AD ＝2，E 是AD 的中点，∠BAD ＝π2，所以BE ⊥AC ．即在题图2中，BE ⊥OA 1，BE ⊥OC ，从而BE ⊥平面A 1OC ，又BC ∥DE ，DE ＝1＝BC ，所以四边形BCDE 为平行四边形，所以CD ∥BE ，所以CD ⊥平面A 1OC ．(2)由已知，平面A 1BE ⊥平面BCDE ，又由(1)知，BE ⊥OA 1，BE ⊥OC ，所以∠A 1OC 为二面角A 1-BE -C 的平面角，所以∠A 1OC ＝π2．如图，以O 为原点，建立空间直角坐标系，因为A 1B ＝A 1E ＝BC ＝ED ＝1，BC ∥ED ，所以B ⎝ ⎛⎭⎪⎫22，0，0，E ⎝ ⎛⎭⎪⎫－22，0，0，A 1⎝⎛⎭⎪⎫0，0，22，C ⎝ ⎛⎭⎪⎫0，22，0，得BC ―→＝⎝ ⎛⎭⎪⎫－22，22，0，A 1C ―→＝⎝⎛⎭⎪⎫0，22，－22， CD ―→＝BE ―→＝(－2，0,0)．设平面A 1BC 的法向量为n 1＝(x 1，y 1，z 1)， 平面A 1CD 的法向量为n 2＝(x 2，y 2，z 2)， 平面A 1BC 与平面A 1CD 的夹角为θ，则⎩⎪⎨⎪⎧n 1·BC ―→＝0，n 1·A 1C ―→＝0，得⎩⎨⎧ －x 1＋y 1＝0，y 1－z 1＝0， 取y 1＝1，得平面A 1BC 的一个法向量为n 1＝(1,1,1)；由⎩⎪⎨⎪⎧ n 2·CD ―→＝0，n 2·A 1C ―→＝0，得⎩⎨⎧x 2＝0，y 2－z 2＝0， 取y 2＝1，得平面A 1CD 的一个法向量为n 2＝(0,1,1)． 从而cos θ＝n 1，n 2＝23×2＝63， 即平面A 1BC 与平面A 1CD 的夹角的余弦值为63．。