巧用割补法解题

【学生版】例析利用割补法解题题型所谓割补法：就是将复杂的或不熟悉的几何图形转化为简单的熟悉的几何图形（如：三角形、正方形、长方形、平行四边形或梯形等）或几何体（如：柱体、锥体和球体）；也就是把一个复杂长度、面积或体积的计算分割成若干个简单图形的有关计算或将一个不易求出长度、面积或体积的几何图形补足为较易计算的几何图形；例如，把曲边形割补成规则图形、把斜棱柱割补成直棱柱、把三棱柱补成平行六面体、把三棱锥补成三棱柱或平行六面体、把多面体切割成锥体（特别是三棱锥）、把不规则的几何体割补成规则的几何体，从而把未知的转化为已知的、把陌生的转化为熟悉的、把复杂的转化为简单的、把不够直观的转化为直观易懂的。

一、“分割”非规则图形为规则图形几何图形或几何体的“分割”，即将已知的几何图形或几何体按照结论的要求，分割成若干个易求长度、面积或体积的几何图形或几何体。

例1、为测出所住小区的面积，某人进行了一些测量工作，所得数据如图所示，则小区的面积是（ ） A ．3＋64 km 2B ．3－64km 2C ．6＋34 km 2D ．6－34km 2【提示】 【解析】 【评注】例2、如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体，截面为ABC ，已知A 1B 1＝B 1C 1＝2，∠A 1B 1C 1＝90°，AA 1＝4，BB 1＝3，CC 1＝2，求： （1）该几何体的体积； （2）截面ABC 的面积。

【提示】 【解析】二、将非规则图形“补形”规则图形几何图形或几何体的“补形”，即将已知的几何图形或几何体按照结论的要求，补全成若干个易求长度、面积或体积的几何图形或几何体。

例3、已知三棱锥A —BCD 的所有棱长都为2，则该三棱锥的外接球的表面积为________例4、如图，在直三棱柱A 1B 1C 1-ABC 中，∠BCA ＝90°，点E ，F 分别为AB ，AC 的中点， 若BC ＝CA ＝CC 1，则B 1E 与A 1F 所成的角的余弦值为________．三、几何体的“割补”几何体的割补，即将已知的几何体按照结论的要求，既要分割又要补全成若干个易求体积的几何体。

割补法在几何题目中的妙用
佛山市高明区沧江中学附属小学 李沃坤
不少学生在解答几何图形的题目都感觉到头痛，其实在解题中应该掌握一定的方法，比如作辅助线、割补法等。

下面就介绍其中一种常用的方法——割补法，这种方法有时候会把一些无从下手的问题迎刃而解。

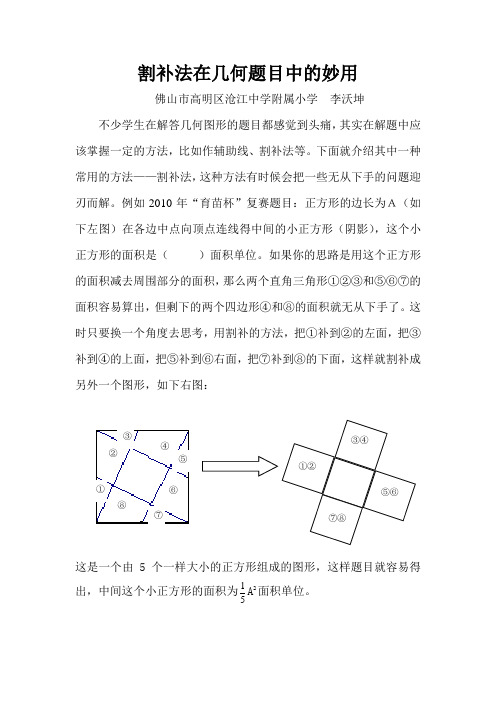
例如2010年“育苗杯”复赛题目：正方形的边长为Ａ（如下左图）在各边中点向顶点连线得中间的小正方形（阴影），这个小正方形的面积是（ ）面积单位。

如果你的思路是用这个正方形的面积减去周围部分的面积，那么两个直角三角形①②③和⑤⑥⑦的面积容易算出，但剩下的两个四边形④和⑧的面积就无从下手了。

这时只要换一个角度去思考，用割补的方法，把①补到②的左面，把③补到④的上面，把⑤补到⑥右面，把⑦补到⑧的下面，这样就割补成另外一个图形，如下右图：
这是一个由5个一样大小的正方形组成的图形，这样题目就容易得出，中间这个小正方形的面积为51A 2面积单位。

① ② ③ ④ ⑤ ⑥ ⑦ ⑧。

割补法求面积经典例题当涉及到计算面积的经典例题时，割补法是一种常用且有效的方法。

下面割补法求面积的经典例题：1. 一个矩形的长为10cm，宽为5cm，求其面积。

解：面积= 长×宽= 10cm ×5cm = 50cm²2. 一个正方形的边长为7cm，求其面积。

解：面积= 边长×边长= 7cm ×7cm = 49cm²3. 一个圆的半径为3cm，求其面积（取π=3.14）。

解：面积= π×半径²= 3.14 ×3cm ×3cm = 28.26cm²4. 一个梯形的上底长为6cm，下底长为8cm，高为4cm，求其面积。

解：面积= （上底长+ 下底长）×高÷2 = （6cm + 8cm）×4cm ÷2 = 28cm²5. 一个三角形的底边长为9cm，高为12cm，求其面积。

解：面积= 底边长×高÷2 = 9cm ×12cm ÷2 = 54cm²6. 一个平行四边形的底边长为10cm，高为6cm，求其面积。

解：面积= 底边长×高= 10cm ×6cm = 60cm²7. 一个等边三角形的边长为5cm，求其面积。

解：面积= （边长²×√3）÷4 = （5cm ×5cm ×√3）÷4 ≈10.83cm ²8. 一个正五边形的边长为8cm，求其面积。

解：面积= （5 ×边长²×√5）÷4 = （5 ×8cm ×8cm ×√5）÷4 ≈110.85cm²9. 一个正六边形的边长为12cm，求其面积。

解：面积= （6 ×边长²×√3）÷4 = （6 ×12cm ×12cm ×√3）÷4 ≈374.12cm²10. 一个扇形的半径为5cm，圆心角为60°，求其面积（取π=3.14）。

巧用割补，化难为易顾介远割补法就是把图形切开，把切下来的那部分移动到其他位置，使题目便于解答；割补法是立体几何解题中的常用技巧，巧妙地对几何体进行分割与拼补，能够简化解题过程。

例如：已知正四面体的棱长为2，求其内切球和外接球的表面积与体积。

分析：本题的解题关键是求出正四面体的内切球和外接球的半径，用何种方法，怎样思维就成了解决本题的关键。

由几何图形我们不难看出球和正四面体都是对称的几何体，所以正四面体的外接球、内切球的球心与正四面体的几何中心重合。

将球心与正四面体的四个顶点连线，就可将这个正四面体分割成四个正四棱锥，这四个正四棱锥的底面分别是正四面体的侧面和底面，高是该正四面体的内切球的半径，侧棱为正四面体的外接球的半径，因此它们的体积相等且这四个正四棱锥的体积的和为正四面体的体积，从而我们可以得出结论：正四面体的外接球的半径是它的内切球的半径的3倍，它们的和等于该正四面的高。

令正四面体的高为h ，则h 2=SA 2-(32AE)2 =(2)2-(233)2,所以h=332；故该正四面体的外接球的半径R=43h=23，其表面积为S=3π；其体积为V=23π。

该正四面体的内切球半径r=41h=63，其表面积为s=31π，其体积v=183π。

如果把思维放开，这个正四面体可以看作是一个棱长为1的正方体ABCD-A /B /C /D /，“切去”四个“角”所对应的三棱锥得到正四面体C /-A /BD ，则该四面体与正方体具有公共的外接球，此时外接球的直径等于该正方体的体对角线的长，即2R=3，所以R=23，再根据R ：r=3：1的关系，该四面体的内切球半径r 就很容易求得了。

高中数学学习的本质是提高学习者的思维品质，快快进行“头脑体操”的锻炼吧，它给你带来快乐和成就感一定会超过鸟叔的《江南style 》！。

巧割善补灵活解题———割补法在职高物理教学中的应用例析摘要：本文以几个物理习题为例，从四个不同方面探讨了割补法在物理学中的应用，进而深化割补转化思想在物理解题过程中的应用，为解决物理学问题提供捷径。

关键词：割补法；割补意识；例析；物理模型；转化思想割补法是物理学中重要的解题方法，它的核心是变复杂为简单，变不规则为规则，即将复杂或不规则的图形，通过分割或补形变成规则的图形，从而避开繁琐的数学运算，使物理过程、意义更加清晰。

割补法在学习中多次出现，作为重要的物理学方法，我们应该掌握它的应用。

下面，笔者通过几个典型例子来谈谈割补法在物理学中的应用，以供读者参考。

例1.两个半球壳拼成的球形容器内部已抽成真空，球形容器的半径为R，大气压强为P。

为使两个半球壳沿图1中箭头方向互相分离，应该施加的力F至少为( )A . 4πR2P B. 2πR2PC.πR2PD.πR2P/2分析：本题取材于著名的“马德堡半球实验”，作用在半球壳上的力有拉力F和大气的压力F＇，刚能使半球壳分离须F＝F＇。

问题是如何计算大气对半球壳的压力F＇。

最典型的错解是选B，即F＝2πR2P。

这是用大气压强直接乘以半球壳的表面积所得结果．因为半球壳各部分受力均指向球心(方向不同)，不可以把球面各部分受到的压力直接相加，而必须按照力的平行四边形定则进行合成。

我们可以构建割补法模型来求解。

解答：将半球壳“取出”，再补上一个底面，如图2所示，显然，大气对此半球壳的压力为零，因此，大气对半球面的压力F＇与对底面的压力F＂必然等大反向，而F＂＝PπR２。

所以F＇＝PπR２。

根据以上分析，本题的正确答案为C。

点评：题目设计虽取自教材实验，但是它又进行了适当的拓展，如果采取常规的方法来解，可能无法下手，特别是大气对半球面压力的具体分析，而采取割补法则解决了这一难题，体现出割补法在解答物理问题上的灵活性。

例2.半径为R的均匀球内切去一个半径为R/2的小球后，质量为M，如图3已知两球内切，在两球心O1、O2的连线上距O1为2R处的质量为m的质点P受到的引力多大？分析：这是一个残缺的模型，球壳对P处质点的引力不能直接应用万有引力定律求解，但是如果将切去的部分填补上去，使其变成一个完整的均匀球体，一个均匀的球体与一个质点间的引力即可应用万有引力定律直接计算。

方法01 割补法对某些物理问题，当待求的量A直接去解很困难或没有条件解时，可设法补上一个量B，割补的原理是使(A+B)成为一个完整的模型，从而使(A+B)变得易于求解，补上去的B也必须容易求解，那样，待求的量A 便可从两者的差值获得，问题就迎刃而解.这就是解物理题时常用的“割补法”.割补法本来是非对称性的物体，通过割补后构成对称性物体，然后再利用对称物体所满足的物理规律进行求解.【调研1】如图所示，阴影区域是质量M半径为R的球体挖去一个小圆球后的剩余部分，所挖去的小圆球的球心O′和大球心间的距离是2R,求球体剩余部分对球体外与球心O距离为2R、质量为m 的质点P的引力.解析：万有引力定律只适用于两个质点间的作用，只有对均匀球体才可将其看作是质量全部集中在球心的一个质点，至于本题中不规则的阴影区，那是不能看作质点来处理的，故可用割补法将挖去的球补上.将挖去的球补上,则完整的大球对球外质点P的引力为：F1=2(2)GMmR=24GMmR，半径为2R的小球的质量：M ' =43π(2R)3×ρ=π(2R)3×34()3MR=18M补上的小球对质点P的引力F2=2'5()2GM mR=24'25G M mR=250GMmR因而挖去小球的阴影对质点P的引力为：F=F1-F2=24GMmR-250GMmR=223100GMmR【调研2】如图所示，把金属丝AB弯成半径r=1m的圆弧，但在AB之间留出宽度为d=2cm、相对来说很小的间隙，将电荷量Q=3.13×10-9C的正电荷均匀分布在金属丝上，求圆心O处的电场强度.解析：中学物理中只讲点电荷场强及匀强电场的计算方法，一个不规则带电体（如本题的缺口的带点环）所产生的场强，没有现成的公式可用.但可以这样想：将圆弧的缺口补上，并且它的电荷密度与缺口的环体原有电荷密度是一样的，这样就形成了一个电荷均匀分布的完整的带电环，环上OdA B处于同一直径两端的微小部分可看作两个相应的点电荷，它们产生的电场在圆心O 处叠加后场强是零，根据对称性可知，带电圆环在圆心O 处的总场强是零.至于补上的带电小段，由题给条件可视为点电荷，它在圆心O 处的场强为E 1是可求的，若题中待求场强为E 2，则由E 1+E 2 =0，便可求得E 2. 设原缺口环所带电荷的线密度为σ，σ=2Q r dπ-，则补上的金属小段带电量Q’=σd ，它在O 处的场强为E 1=k2'Q r= k2(2)Qd r d r π-，代入数据得E 1=9×10-2N/C. 设待求的场强为E 2，由E 1+E 2=0可得E 2=-E 1=-9×10-2N/C ，负号表示E 2与E 1方向相反，即E 2的方向向右，指向缺口.【调研3】静电学理论指出，对于真空区域，只要不改变该区域内的电荷分布及区域边界的电势分布，此区域内的电场分布就不会发生改变。

割补法在数学解题中的妙用
宋培武
【期刊名称】《数学学习与研究：教研版》
【年(卷),期】2017(000)019
【摘要】割补法在数学解题中应用广泛.其中的＂割＂是指对某图形进行分割;＂补＂是针对某特殊图形的缺失进行补充.＂割＂与＂补＂常常是同时发生,有时也单独发生.＂割补＂的目的是实现数学问题由一般图形向特殊图形、由陌生领域向熟悉领
域转化,它是＂化归思想＂的具体体现.这一思想不仅应用于几何解题,也被迁移到代数解题中.一、几何题型（一）只＂割＂不＂补＂例1在四边形ABCD
中,∠B=∠D=90°A=135°,
【总页数】1页(P142-142)
【作者】宋培武
【作者单位】安徽省阜阳市颍州区程集镇中心学校,安徽阜阳236000
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.浅谈割补法在数学解题中的应用 [J], 陈兴玉
2.数学解题中灵活变通策略的妙用 [J], 黄桂君;郭有春
3.浅谈割补法在数学解题中的应用 [J], 陈兴玉
4.转化思想在小学数学解题中的妙用 [J], 吕志远
5.小学数学解题中转化思想之妙用 [J], 孙佐君
因版权原因，仅展示原文概要，查看原文内容请购买。

利用割补法巧解几何题割补法在初中数学竞赛中经常用到，实际上它也广泛应用于一般几何证明题中。

下面我就从四个方面来说明割补法在几何证明中的重要性：一．利用垂直与特殊角割补成特殊三角形例1：四边形ABCD中，∠B=∠D=90°，∠A=135°，AD=2，BC=6 H求四边形ABCD面积解：由题意知：∵∠C=45°，利用∠B=90° D∠C=45°，延长BA、CD交于H，将图形割补成特殊△HBC（等腰Rt三角形） A易求：HD=AD=2 HB=BC=6 ，∴S四边形ABCD=1/2·6·6—1/2·2·2=16B C 例2：四边形ABCD中，AB=8，BC=1，∠DAB H =30°，∠ABC=60°，四边形ABCD面积为5√３， D求AD长 C解：由题意知：∠A=30°，∠B=60°利用已知延长AD、BC交于H，将图形割补成特殊三角形。

B ∵∠A=30°，AB=8∴BH=4，AH=4√３，CH=3 A∴S△ABH=8√３，S△HDC=3√３=1/2HC·DH∴DH=2√３AD=2√３D思考题：1．已知：四边形ABCD中，AB=2，CD=1， C ∠A=60°，∠B=∠D=90°求四边形ABCD面积A B2．四边形ABCD中，∠ABC =135°， D∠BCD=120°，AB=2√６，BC=5√３，CD=6求AD长 AC B二．利用角平分线与垂直割补全等例1：△ABC是等腰Rt三角形，∠A=90°，AB=AC， F BD平分∠ABC，CE⊥BD交BD延长线于 E求证：BD=2CE解：∵BD平分∠ABC，且CE⊥BE， A∴延长BA、CE交于F，将图形割补成 E轴对称图形△BCF即：△FBE≌△CBE， D易证：△ABD≌△ACF∴BD=CF=2CE B C思考题：1．已知：AB=3AC，AD平分∠BAC，BD⊥AD，AD交于BC于O C D求证：OA=OD OA B2．已知：锐角△ABC中，∠B=2∠C A∠B的平分线与AD垂直求证：AC=2BDDB C三．利用互补割补全等例1：五边形ABCDE中，∠ABC=∠AED C D =90°AB=CD=AE=BC+DE=1求五边形ABCDE面积 B解：延长CB到F，使BF=DE连AD、AF、AC E 易证：△AED≌△ABF， F△ADC≌△AFC，∴五边形ABCDE面积为△ACF面积的2倍，即等于 1 A例2：在四边形ABCD中，已知：AB= A E AD,∠BAD=∠BCD=90°，AH⊥BC，且AH=1求四边形ABCD面积 D 解：过A作AE⊥AH交CD延长线于E易证：△ABH≌△ADE∴AH=AE=1∴四边形ABCD面积为正方形AHCE面积等于 1 B H C 思考题：1．五边形ABCDE中，AB=AE， ABC+DE=CD，∠ABC+∠AED=180°，连AD E求证：AD平分∠CDEDBC。