割补法巧算面积
- 格式:ppt
- 大小:877.99 KB
- 文档页数:13



割补法求面积经典例题当涉及到计算面积的经典例题时,割补法是一种常用且有效的方法。
下面割补法求面积的经典例题:1. 一个矩形的长为10cm,宽为5cm,求其面积。
解:面积= 长×宽= 10cm ×5cm = 50cm²2. 一个正方形的边长为7cm,求其面积。
解:面积= 边长×边长= 7cm ×7cm = 49cm²3. 一个圆的半径为3cm,求其面积(取π=3.14)。
解:面积= π×半径²= 3.14 ×3cm ×3cm = 28.26cm²4. 一个梯形的上底长为6cm,下底长为8cm,高为4cm,求其面积。
解:面积= (上底长+ 下底长)×高÷2 = (6cm + 8cm)×4cm ÷2 = 28cm²5. 一个三角形的底边长为9cm,高为12cm,求其面积。
解:面积= 底边长×高÷2 = 9cm ×12cm ÷2 = 54cm²6. 一个平行四边形的底边长为10cm,高为6cm,求其面积。
解:面积= 底边长×高= 10cm ×6cm = 60cm²7. 一个等边三角形的边长为5cm,求其面积。
解:面积= (边长²×√3)÷4 = (5cm ×5cm ×√3)÷4 ≈10.83cm ²8. 一个正五边形的边长为8cm,求其面积。
解:面积= (5 ×边长²×√5)÷4 = (5 ×8cm ×8cm ×√5)÷4 ≈110.85cm²9. 一个正六边形的边长为12cm,求其面积。
解:面积= (6 ×边长²×√3)÷4 = (6 ×12cm ×12cm ×√3)÷4 ≈374.12cm²10. 一个扇形的半径为5cm,圆心角为60°,求其面积(取π=3.14)。

割补法求面积
割补法求面积是一种常见的几何学方法,它适用于各种形状的图形,包括矩形、三角形、梯形等等。
具体操作方法是先将图形切割成若干个简单的几何形状,然后利用这些形状的面积之和来求出整个图形的面积。
例如,对于一个梯形,我们可以将其割成一个矩形和两个三角形,然后分别计算这些简单形状的面积,最后将它们相加即可得到梯形的面积。
在实际应用中,割补法求面积的优点在于能够有效地简化计算,尤其是对于复杂的图形而言。
同时,这种方法还能够帮助我们更好地理解几何形状的结构和特性。
总之,割补法求面积是一种非常实用的几何学方法,对于学生和工程师都是非常有用的工具。
- 1 -。

割补法巧算面积割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH 的面积.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。

割补法求三角形面积
割补法是计算三角形面积的一种常用方法。
根据割补法,给定一个三角形,我们可以在三角形内部或外部构造一些辅助线段,将三角形分割成更简单的几何形状,以便计算其面积。
以下是使用割补法计算三角形面积的一般步骤:
1. 画出给定的三角形ABC,并确保已知三个顶点A、B、C。
2. 选择一个合适的点D,使得线段AD与线段BC平行。
3. 测量线段AD的长度,记为h。
4. 计算线段AD与线段BC的长度比值k。
这可以通过测量线段AD和线段AB的长度,并计算k = AD / AB来实现。
5. 计算三角形ABD的面积:SABD = (1/2) * AB * h。
6. 计算三角形ABC的面积:SABC = k^2 * SABD。
7. 得到三角形ABC的面积SABC。
请注意,割补法只是一种计算三角形面积的方法之一,具体的步骤可能会因情况而异。
对于不规则三角形或无法使用割补法的情况,可以尝试其他计算面积的方法,如海伦公式或向量法。

小升初几何之---用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB 弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。


四年级第十一讲割补法巧算面积◆温故知新:1. 用割补法把不规则图形变成规则图形计算面积。
2.正方形、等腰直角三角形、等边三角形、正六边形等已知图形分割成小块,与所求图形面积相联系。
◆练一练1、在图中,五个小正方形的边长都是2厘米,求三角形的面积。
ABC2、图中小正方形和大正方形的边长分别是4厘米和6厘米。
阴影部分的面积是多少平方厘米?◆例题展示例题1图中的数字分别表示对应线段的长度,试求这个多边形的面积。
(单位:厘米)练习1如图所示,在正方形内部有一个长方形。
已知正方形的边ABCD EFGH ABCD 长是6厘米,图中线段都等于2厘米。
求长方形的面积。
、EFGHAE AH例题2如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连。
请问:图中阴影部分的面积总和等于多少平方厘米?练习2如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,再连接大正方形的两条对角线。
请问:图中阴影部分的面积总和等于多少平方厘米?例题3如图所示,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD 中点,P是EF中点。
请问三角形MNP的面积是多少平方厘米?练习3 如图所示,正六边形ABCDEF的面积是36平方厘米,M、N、P、Q、R、S分别是AB、BC、CD、DE、EF、FA的中点。
请问:阴影正六边形MNPQRS的面积是多少平方厘米?例题4 如图,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点。
已知图a中阴影部分的面积是294平方分米。
请问:图b中阴影部分的面积是多少平方分米?练习4如图,把两个同样大小的正方形分别分成5×5和6×6的方格表。
其中“G”形阴影部分的面积是558,请问“S”形阴影部分的面积是多少?◆拓展提高拓展1如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A 的面积是36平方厘米,那么正方形B的面积是多少平方厘米?练习1如图,在两个相同的等腰直角三角形中各作一个正方形,如果三角形A的面积是16平方厘米,那么三角形B的面积是多少平方厘米?拓展2 如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(图中3和7的单位是厘米)练习2 如图,在等腰梯形ABCD中,角B是60度,线段AB、AD、CD长度相等。
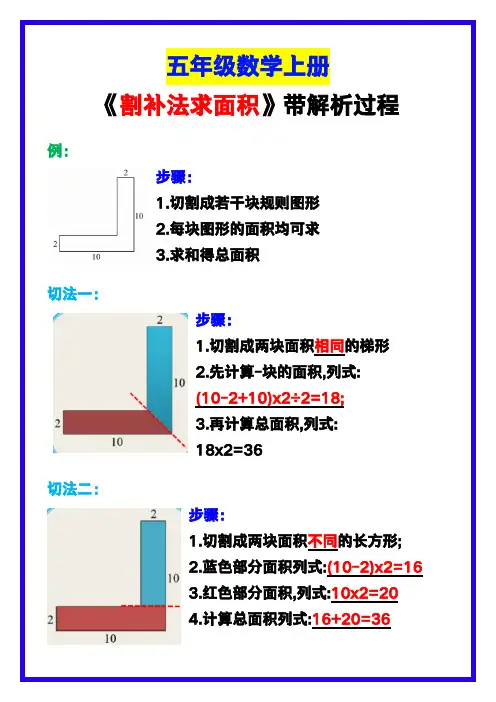
五年级数学上册《割补法求面积》带解析过程例:步骤:1.切割成若干块规则图形2.每块图形的面积均可求3.求和得总面积切法一:步骤:1.切割成两块面积相同的梯形2.先计算-块的面积,列式:(10-2+10)x2÷2=18;3.再计算总面积,列式:18x2=36切法二:步骤:1.切割成两块面积不同的长方形;2.蓝色部分面积列式:(10-2)x2=163.红色部分面积,列式:10x2=204.计算总面积列式:16+20=36切法三:步骤:1.切割成两块面积不同的长方形;2.蓝色部分面积,列式:10x2=203.红色部分面积,列式:(10-2)x2=164.计算总面积,列式:20+16=36题1:求图中阴影面积。
(单位:厘米)【解析】:解法一:如下图,把图形分割后,将①号扇形拼到A处,将②号扇形拼到B处,把求阴影部分面积转化为求长为半圆直径、宽为半圆半径的长方形的面积。
所求阴影部分面积为:4×(4÷2)=8(平方厘米)解法二:如下图,把图形分割后,将①号弓形拼到A处,将②号弓形拼到B处,把求阴影部分面积转化为求两个三角形的面积和。
拼成的每个三角形的底是半圆直径长4厘米,高为半圆半径长是直径的一半。
所求阴影部分面积为:4×(4÷2)÷2×2=8(平方厘米)。
题2:求图中阴影面积。
【解析】:如下图,根据图形的对称性对图形进行分割,再将①号阴影部分拼到A空白处,把求阴影部分面积,转化为求长为b、宽为a的长方形的面积。
则所求阴影部分面积为ab。
题3:求阴影部分的面积。
(单位:分米)【解析】:如下图,根据图形的对称性对图形进行分割,再将①号弓形拼到A空白处,将②号弓形拼到B空白处,把求阴影部分面积,转化为求1/4圆周所对应的弓形的面积。
用上图1/4圆的面积减去三角形ABC的面积,可得所求阴影部分面积为:3.14×22÷4-2×2÷2=10.56(平方分米)。

割补法是一种常用的求面积的方法,其基本思想是将一个复杂的图形割补成几个简单的规则图形,然后利用这些规则图形的面积公式来求解原图形的面积。
以下是使用割补法求面积的一些技巧:
1.观察图形:首先观察要计算的图形,看是否可以通过割补将其变为简单的规则图形。
2.选择割补方式:根据图形的特点,选择合适的割补方式。
割补方式的选择对于简化问题非常重要。
3.计算规则图形面积:对于割补后的规则图形,使用相应的面积公式进行计算。
4.求和或相减:如果图形是通过割补多个部分得到的,那么需要将各部分的面积相加或相减,以得到原图形的面积。
5.验证答案:完成计算后,要验证答案是否正确。
可以通过将答案代回原图形,看是否与原图形的面积相等来进行验证。
下面是一个使用割补法求面积的例子:
题目:求下图中阴影部分的面积(单位:cm²)。
![阴影部分为不规则图形]
(请根据您所使用的软件或平台的功能进行适当的调整或
绘制)
解:观察图形,发现可以将阴影部分割补成一个半圆和一个等腰直角三角形。
半圆的半径为r = 5cm,面积为 21×π×r2。
等腰直角三角形的底为b = 10cm,高为h = 5cm,面积为 21×b×h。
因此,阴影部分的面积为半圆面积加上三角形面积,即 21×π×52+21×10×5=39.25cm2。
割补法求面积
割补法是一种求解平面图形面积的方法,其基本思想是将图形分割成若干个简单的图形,然后分别求解这些简单图形的面积,最后将它们加起来得到整个图形的面积。
具体操作方法如下:
1. 将要求面积的图形按照一定的方法分割成若干个简单图形,如三角形、矩形、梯形等。
2. 对每个简单图形,利用相应的公式计算出其面积。
3. 将所有简单图形的面积加起来,就得到了整个图形的面积。
需要注意的是,割补法要求分割后的简单图形面积能够计算,而且分割的方法应当尽可能简单,使得计算面积的公式易于应用。
此外,对于一些复杂的图形,可能需要进行多次分割才能求得其面积。
割补法是求解平面图形面积的一种重要方法,广泛应用于数学、物理、工程等领域。
通过掌握割补法,能够更加深入地理解平面图形的性质,提高数学素养和解决实际问题的能力。
- 1 -。
割补法求面积总结
嘿,朋友们!今天咱就来聊聊这超有意思的割补法求面积!
咱就说啊,那求面积有时候就像打游戏过关,遇到难题了,割补法就好
比一把神奇的钥匙!比如说,有个不规则图形,歪七扭八的,看着就头疼,咋求面积呀?这时候割补法就闪亮登场啦!咱把它割成几块规则的图形,或者给它补上一块,让它变成咱熟悉的图形。
就像上次我遇到一个四边形,哎呀,那叫一个复杂!我就琢磨着,能不
能给它变一变呢?于是我就大胆地把它分割成了两个三角形和一个矩形,哇塞,瞬间感觉柳暗花明又一村啊!这不就好算多了嘛!
还有啊,有时候就像拼图一样,把那些零散的部分通过补的方式凑成完
整的形状。
好比有个图形缺了一角,咱给它补上,嘿,马上就能用熟悉的公式去计算啦!这多神奇呀!
割补法就像是一个魔法,能把那些让人头疼的面积问题变得轻松又有趣!它可不是死板的方法哦,是需要我们开动脑筋,大胆尝试的呢!想想看,当
你通过割补法成功求出一个复杂图形的面积时,那成就感,简直爆棚啊!难道不是吗?就像你解开了一道超级难的谜题,心里那个爽呀!
所以呀,大家可千万别小瞧了这割补法,它真的是我们求面积的得力小助手呢!只要我们勇于尝试,善于发现,用割补法就能轻松搞定那些看似不可能的面积问题啦!以后遇到求面积的难题,可别再犯愁咯,赶紧想起咱的割补法吧!。
巧用割补法解求解二次函数中的面积问
题
割补法是一种解决函数面积问题的有效方法,它可以用来计算二次函数中的面积。
割补法的基本思想是,将一个函数的面积分解为两个函数的面积之和,其中一个函数是原函数的一部分,另一个函数是原函数的补函数。
首先,我们需要确定二次函数的补函数,即将原函数的曲线上的点按照一定的规律反向移动,使其形成一条新的曲线,这条曲线就是补函数。
接下来,我们可以将原函数的面积分解为两个函数的面积之和,即原函数的面积加上补函数的面积。
最后,我们可以使用积分法来计算两个函数的面积,然后将两个函数的面积相加,就可以得到原函数的面积。
因此,割补法是一种有效的解决二次函数中面积问题的方法,它可以帮助我们快速准确地计算出二次函数的面积。