下载文档原格式
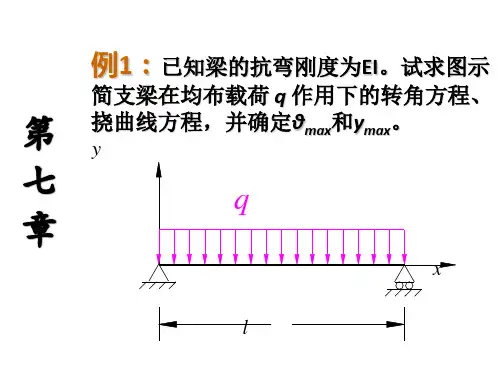
梁的抗弯曲刚度计算公式梁是工程结构中常见的构件，其抗弯曲性能对结构的整体稳定性和安全性具有重要影响。
在工程设计中，需要对梁的抗弯曲性能进行计算和分析，以确保结构的安全可靠。
梁的抗弯曲刚度是评价其抗弯曲性能的重要参数之一，本文将介绍梁的抗弯曲刚度计算公式及其应用。
梁的抗弯曲刚度是指梁在受到外力作用时抵抗弯曲变形的能力。
在工程设计中，通常使用弹性理论来计算梁的抗弯曲刚度。
根据弹性理论，梁的抗弯曲刚度与梁的几何形状、材料性能和受力情况有关。
一般来说，梁的抗弯曲刚度可以通过以下公式进行计算：EI = K (b h^3) / 12。
其中，EI表示梁的抗弯曲刚度，单位为N·m^2；K为梁的截面形状系数；b为梁的宽度，单位为m；h为梁的高度，单位为m。
上述公式中的截面形状系数K反映了梁的截面形状对其抗弯曲性能的影响。
对于不同形状的截面，其截面形状系数K也不同。
一般来说，矩形截面的梁的截面形状系数K为1/3，而对于其他形状的截面，则需要根据具体情况进行计算。
在实际工程中，可以通过有限元分析等方法来确定梁的截面形状系数K。
梁的抗弯曲刚度计算公式可以应用于不同类型的梁，包括悬臂梁、简支梁和连续梁等。
在实际工程设计中，需要根据具体的受力情况和结构要求来选择合适的计算方法。
下面将分别介绍悬臂梁、简支梁和连续梁的抗弯曲刚度计算方法。
对于悬臂梁而言，其一端固定，另一端悬空。
在计算悬臂梁的抗弯曲刚度时，需要考虑悬臂梁的受力情况和截面形状。
一般来说，可以通过悬臂梁的截面形状系数K和悬臂长度来计算悬臂梁的抗弯曲刚度。
具体计算方法如下：EI = K (b h^3) / 3 L。
其中，L表示悬臂长度，单位为m。
对于简支梁而言，其两端都可以自由转动。
在计算简支梁的抗弯曲刚度时，需要考虑简支梁的受力情况和截面形状。
一般来说，可以通过简支梁的截面形状系数K和梁长来计算简支梁的抗弯曲刚度。
具体计算方法如下：EI = K (b h^3) / 3 L。
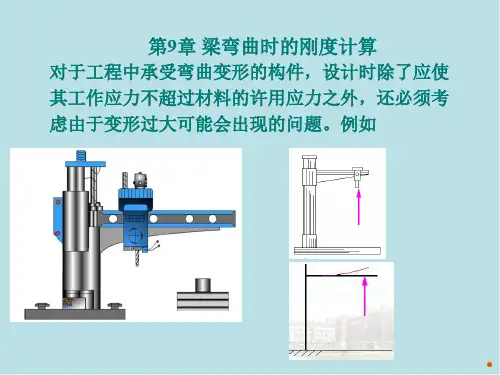
静态刚度计算公式
1.梁的弯曲刚度:
梁的弯曲刚度计算公式如下所示：
$$
EI=\frac{1}{k}
$$
其中，E表示梁的杨氏模量，I表示梁的截面惯性矩，k表示梁的曲率。
2.柱的弯曲刚度:
柱的弯曲刚度计算公式如下所示：
$$
EI=\frac{\pi^2EI}{l^2}
$$
其中，E表示柱的杨氏模量，I表示柱的截面惯性矩，l表示柱的长度。
3.弹簧的刚度:
弹簧的刚度计算公式如下所示：
$$
k=\frac{F}{\delta}
$$
其中，k表示弹簧的刚度，F表示作用在弹簧上的力，
$\delta$表示弹簧的形变。
4.板的刚度:
板的刚度计算公式如下所示：
$$
k=\frac{D}{t}
$$
其中，k表示板的刚度，D表示板的弯曲刚度矩，t表示板的厚度。
5.圆环的刚度:
圆环的刚度计算公式如下所示：
$$
k=\frac{k_1k_2}{k_1+k_2}
$$
其中，k表示圆环的刚度，k1和k2表示圆环内外半径的刚度。
需要注意的是，在实际工程中，刚度计算通常还要考虑材料的弹性、应力分布等因素，因此以上列举的公式只是一些常见
情况下的刚度计算公式，具体情况需要根据实际工程而定。
此外，不同国家和行业的标准和规范可能会有所差异，需要根据实际情况参考相应的标准和规范进行计算。
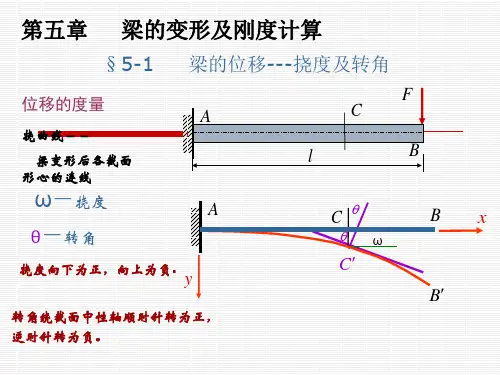
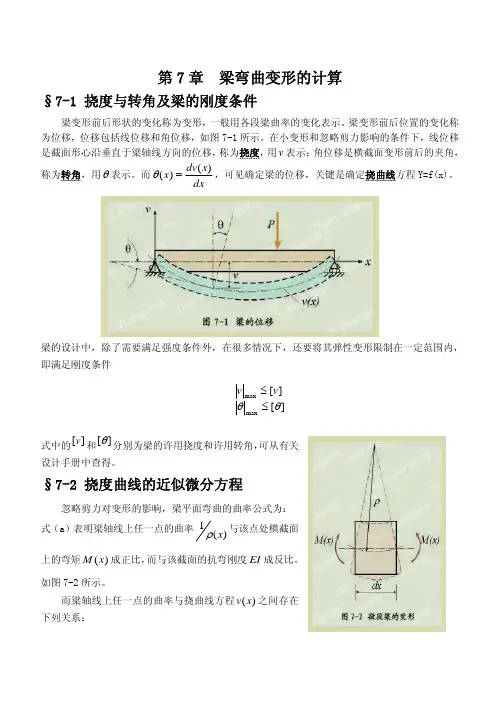
第7章 梁弯曲变形的计算§7-1 挠度与转角及梁的刚度条件梁变形前后形状的变化称为变形，一般用各段梁曲率的变化表示。
梁变形前后位置的变化称为位移，位移包括线位移和角位移，如图7-1所示。
在小变形和忽略剪力影响的条件下，线位移是截面形心沿垂直于梁轴线方向的位移，称为挠度，用v 表示；角位移是横截面变形前后的夹角，称为转角，用θ表示。
而dxx dv x )()(=θ，可见确定梁的位移，关键是确定挠曲线方程Y=f(x)。
梁的设计中，除了需要满足强度条件外，在很多情况下，还要将其弹性变形限制在一定范围内，即满足刚度条件][][max max θθ≤≤v v式中的和][v ][θ分别为梁的许用挠度和许用转角，可从有关设计手册中查得。
§7-2 挠度曲线的近似微分方程忽略剪力对变形的影响，梁平面弯曲的曲率公式为： 式（a）表明梁轴线上任一点的曲率)(1x ρ与该点处横截面上的弯矩成正比，而与该截面的抗弯刚度)(x M EI 成反比。
如图7-2所示。
而梁轴线上任一点的曲率与挠曲线方程v 之间存在下列关系：)(xEIx M x )()(1=ρ （a） 232221)(1⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±dx dv dx vd x ρ （b）将上式代入式（a），得到EIx M dx dv dx v d )(12322=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±（c） 小挠度条件下，1<<=θdxdv，式（c）可简化为： EI x M dxv d )(22=±（d）在图7-3所示的坐标系中，正弯矩对应着22dx vd 的正值（图7-3a），负弯矩对应着22dxvd 的负值（图7-3b），故式（d）左边的符号取正值EI x M dx v d )(22= （8-1）式（7-1）称为小挠度曲线微分方程，简称小挠度微分方程。
显然，小挠度微分方程仅适用于线弹性范围内的平面弯曲问题。
