y
M
M
M<0 w’’<0
O O
x
曲线向下凸 时: w’’>0, M>0
因此, M与w’’的正负号相同。 y
M
M
w
M (x)
(1 w2 )32 EI
M>0 w’’>0
x
w
(1
w2
)
3 2
M (x) EI
由于挠曲线是一条非常平坦的曲线, w'2远比1小, 可以略去不计, 于是上式可写成
w M (x) EI
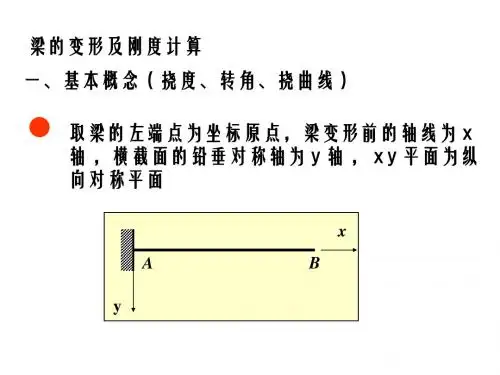
转角(): 横截面 y
绕中性轴(即Z轴)转 A 过的角度(或角位 移), 称为该截面 的 转 角 (Slope rotation angle) 。
F CBx
w(挠度)
C1
(转角)
9.1 工程实际中的弯曲变形问题
挠度和转角符号的规定:
挠度:在图示坐标系中, 向上为正, 向下为负。
转角: 逆时针转向为正,顺时针转向为负。
在这种情况下, 梁在几项载荷 (如集中力、集中力 偶或分布力)同时作用下某一横截面的挠度和转角, 就 分别等于每项载荷单独作用下该截面的挠度和转角的 叠加。此即为叠加原理。
例1:一抗弯刚度为EI的简支梁受荷载如图所示。
试按叠加原理求梁跨中点的挠度wC 和支座处横
截面的转角A ,B 。
q Me
解:将梁上荷载分为两项 A
C
B
简单的荷载。
l
wC wCq wCM
5ql4 M el2 384EI 16EI
A Aq AM
ql3 M el 24EI 3EI
B
Bq BM
ql3 M el 24EI 6EI
例2:试利用叠加法, 求图示抗弯刚度为EI的简支