梁的弹性弯曲变形与刚度计算问题
- 格式:ppt
- 大小:1.96 MB
- 文档页数:69

梁的抗弯曲刚度计算公式梁是工程结构中常见的构件,其抗弯曲性能对结构的整体稳定性和安全性具有重要影响。
在工程设计中,需要对梁的抗弯曲性能进行计算和分析,以确保结构的安全可靠。
梁的抗弯曲刚度是评价其抗弯曲性能的重要参数之一,本文将介绍梁的抗弯曲刚度计算公式及其应用。
梁的抗弯曲刚度是指梁在受到外力作用时抵抗弯曲变形的能力。
在工程设计中,通常使用弹性理论来计算梁的抗弯曲刚度。
根据弹性理论,梁的抗弯曲刚度与梁的几何形状、材料性能和受力情况有关。
一般来说,梁的抗弯曲刚度可以通过以下公式进行计算:EI = K (b h^3) / 12。
其中,EI表示梁的抗弯曲刚度,单位为N·m^2;K为梁的截面形状系数;b为梁的宽度,单位为m;h为梁的高度,单位为m。
上述公式中的截面形状系数K反映了梁的截面形状对其抗弯曲性能的影响。
对于不同形状的截面,其截面形状系数K也不同。
一般来说,矩形截面的梁的截面形状系数K为1/3,而对于其他形状的截面,则需要根据具体情况进行计算。
在实际工程中,可以通过有限元分析等方法来确定梁的截面形状系数K。
梁的抗弯曲刚度计算公式可以应用于不同类型的梁,包括悬臂梁、简支梁和连续梁等。
在实际工程设计中,需要根据具体的受力情况和结构要求来选择合适的计算方法。
下面将分别介绍悬臂梁、简支梁和连续梁的抗弯曲刚度计算方法。
对于悬臂梁而言,其一端固定,另一端悬空。
在计算悬臂梁的抗弯曲刚度时,需要考虑悬臂梁的受力情况和截面形状。
一般来说,可以通过悬臂梁的截面形状系数K和悬臂长度来计算悬臂梁的抗弯曲刚度。
具体计算方法如下:EI = K (b h^3) / 3 L。
其中,L表示悬臂长度,单位为m。
对于简支梁而言,其两端都可以自由转动。
在计算简支梁的抗弯曲刚度时,需要考虑简支梁的受力情况和截面形状。
一般来说,可以通过简支梁的截面形状系数K和梁长来计算简支梁的抗弯曲刚度。
具体计算方法如下:EI = K (b h^3) / 3 L。

梁的强度和刚度计算强度是指梁抵抗外力的能力。
梁的强度计算一般包括了两个方面:弯曲强度和剪切强度。
其中,弯曲强度是指梁在受到弯曲作用时的承载能力,剪切强度是指梁在受到剪切力作用时的承载能力。
弯曲强度的计算通常基于弹性理论,其中最常用的方法是根据梁的截面形状和材料的弹性模量来计算梁的截面抵抗力矩。
弹性模量是材料的一种力学性质,它衡量了材料在受力后产生的应变程度。
根据梁的截面形状和边界条件,可以计算出梁在弯曲作用下的最大应力和最大应变。
将最大应力与材料的弯曲强度进行比较,就可以判断梁是否满足设计要求。
剪切强度的计算也是基于弹性理论。
梁在受到剪切力作用时,梁内部会发生剪切变形。
剪切强度的计算包括两个方面:剪切应力和剪切变形。
剪切应力是指剪切力对梁截面的作用,剪切变形是指梁截面产生的剪切位移。
剪切强度的计算要求同时满足两个条件:剪切应力小于材料的剪切强度,剪切变形小于允许的变形限制。
刚度是指梁在受到力作用后的变形程度。
梁的刚度决定了梁的承载能力和结构的稳定性。
刚度的计算通常考虑梁的弹性变形和塑性变形两个方面。
弹性变形是指梁在小荷载下的弯曲变形,主要涉及梁的截面形状、材料的弹性模量和梁的长度等因素。
塑性变形是指梁在大荷载下的弯曲变形,主要涉及梁的屈服强度、截面形状和材料的塑性性质等因素。
根据梁的受力情况,可以计算出梁的弯曲刚度和剪切刚度。
弯曲刚度表示梁在受到弯曲作用时的抵抗变形能力,剪切刚度表示梁在受到剪切力作用时的抵抗变形能力。
在梁的强度和刚度计算中,需要根据具体的工程要求和设计规范进行。
梁的截面形状、材料的性质和受力情况都会对强度和刚度的计算结果产生影响。
因此,工程师需要根据具体情况选择适当的计算方法和模型进行计算。
同时,还需要进行合理的验算和对比,确保梁的设计满足强度和刚度的要求。
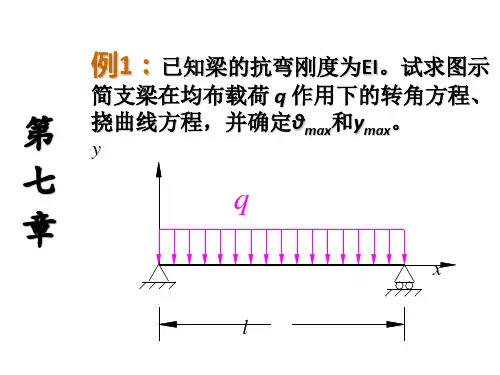
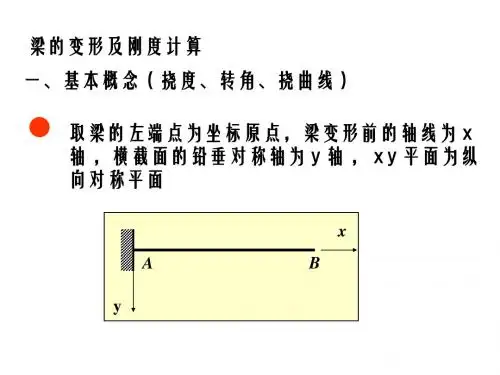






梁线刚度计算公式
梁线刚度可以通过弯曲、拉伸和剪切三种形式进行计算。
具体的公式如下:
弯曲刚度计算公式:
梁线的弯曲刚度可以通过以下公式计算:
EI = k * D / (2 * Phi)
其中EI表示梁的弯曲刚度,k表示梁的弹性系数,D表示梁的弯曲变形,Phi表示梁的弯曲角度。
如果梁的截面形状、材料和长度确定,那么EI值也是固定的。
拉伸刚度计算公式:
梁线的拉伸刚度可以通过以下公式计算:
EA = F / deltaL
其中EA表示梁的拉伸刚度,F表示梁的受力大小,deltaL表示梁的拉伸变形。
如果梁的截面积和材料确定,那么EA值也是固定的。
剪切刚度计算公式:
梁线的剪切刚度可以通过以下公式计算:
GA = k / tau
其中GA表示梁的剪切刚度,k表示梁的剪切模量,tau表示材料的剪切应力。
剪切刚度与梁线的剪切变形有关,当材料的剪切应力发生变化时,剪
切变形也会相应改变。
需要注意的是,梁线的刚度计算公式根据不同的应力状态而有所不同。
在实际工程中,根据梁的材料、截面形状和受力情况,通常采用适当的刚
度计算公式来计算梁线的刚度。
梁线刚度的计算是结构力学中的基础问题之一,通过准确计算梁线的
刚度,可以帮助工程师在设计过程中确保结构的稳定性和安全性。
同时,
梁线刚度的计算也为设计者提供了选择材料和截面形状的依据,以满足实
际工程要求。

§6-3 梁弯曲时的变形和刚度条件课时计划:讲授3学时教学目标:1.理解梁弯曲变形时挠度和转角的概念;2.掌握梁的刚度计算方法及刚度条件。
教材分析:1.重点为梁弯曲变形时挠度和转角的概念;2.难点为梁的刚度计算方法及刚度条件。
教学设计:本节课的主要内容是讲解梁弯曲变形时挠度和转角的概念以及梁的刚度计算方法。
重点为梁弯曲变形时挠度和转角的概念,在此基础上进一步掌握梁的刚度计算方法并建立梁弯曲时的刚度条件。
通过对教材例题的讲解,使学生在此过程中进一步理解弯曲变形,进而学会利用弯曲梁的刚度条件解决工程实际问题。
第1学时教学内容:一、挠度和转角本节课的主要内容是讲解梁弯曲变形时挠度和转角的概念。
因为材料力学研究强度与刚度,强度问题要计算应力,刚度问题要计算变形,本节讲梁的弯曲变形。
图示为简支梁弯曲变形时,变形前梁轴线是直线,受力F 弯曲变形后轴线是光滑平面曲线,变形前后梁轴线简化如下图所示。
横截面nn 移''n n ,形心C 到'C 点。
横截面形心在垂直于原轴线方向的位移,称为截面的挠度,用ω表示;横截面相对于原来位置转过的角度,称为该截面的转角,用θ表示。
截面形心轴线方向位移很小,高阶微量,可省略不计。
弯曲变形后梁的轴线变成一条连续而光滑的平面曲线,称为挠度曲线,简称挠曲线。
在图示的Oxw 坐标系中,表示挠曲线的方程为w =w(x)称为挠度方程。
由于轴线是各截面形心的连线,故该方程中的x 为变形前截面位置的横坐标,ω为变形后该截面的挠度。
由于截面转角等于挠度曲线在该截面的切线与x 轴的夹角,小变形有:()x w x w '==≈d d θθtan即任一截面转角近似等于挠度方程对x 的一阶导数。
所以挠度和转角的数值都可以由挠度方程及其一阶导数确定,只要有了挠度方程,就可以计算挠度和转角。
公式中挠度向上为正值,向下为负值;转角逆时针方向为正值,顺时针方向为负值。
由表可知,在一定外力作用下,梁的挠度、转角都和材料的弹性模量E 与截面惯性矩z I 的乘积z EI 成反比。
简支梁刚度
简支梁刚度指的是在外力作用下,梁发生弯曲变形时所具有的抵抗能力。
梁的刚度主要取决于梁的几何尺寸、材料特性以及支承条件等因素。
对于简支梁而言,其刚度与梁的截面形状、截面面积、材料的弹性模量和长度等因素相关。
简支梁的刚度可以通过弯曲刚度来描述。
弯曲刚度是指在相同外力作用下,梁发生相同的弯曲变形所需施加的弯矩大小。
弯曲刚度的计算公式为EI,其中E是梁的弹性模量,I是梁的截面惯性矩。
在实际应用中,我们通常使用挠度来表示简支梁的刚度。
挠度是指在相同外力作用下,梁的最大变形量。
挠度越小,说明梁的刚度越大。
挠度的计算需要考虑梁的长度、截面形状、截面尺寸等因素。
在工程实践中,为了满足建筑物的使用要求,要求简支梁的刚度应该在一定范围内。
一般来说,短梁的刚度比较高,而长梁的刚度相对较低。
此外,梁的截面形状、尺寸和所选材料的弹性模量也会影响梁的刚度。
在实际设计中,需要综合考虑各种因素,确定合理的梁的尺寸和材料,以满足工程需求。
总之,简支梁的刚度取决于多种因素,包括梁的长度、截面形状、尺寸和材料的弹性模量等。
在工程实践中,需要综合考虑各种因素,以确定合理的梁的尺寸和材料,以达到满足工程需求的目的。