PR部分习题解答

pr练习题合集在公关（PR）领域中，练习题是一种常见的培训和学习方法，通过解决实践问题来提高专业能力。

本篇文章将为您提供一系列的PR练习题，以帮助您巩固和应用所学知识。

无论您是初学者还是有经验的从业者，这些练习题都能为您提供挑战和成长的机会。

1. 媒体关系a) 选择一个您所关注的行业和目标媒体，列举三个重要的媒体渠道。

b) 针对以上三个媒体渠道，提出一项具有吸引力的新闻故事或独家报道的想法。

c) 想象自己是一家公司的PR代表，描述您将如何与这三个媒体渠道建立和维护关系。

2. 社交媒体管理a) 选择一个热门的社交媒体平台，例如Facebook、Instagram或Twitter。

b) 根据您所选择的平台，提出三个增加粉丝或关注者数量的策略。

c) 针对您所选择的平台，制定一个月的社交媒体内容计划，包括发布时间、内容主题和目标受众。

3. 危机管理a) 阅读一篇与危机管理相关的案例，例如某家公司的产品质量问题或高管丑闻。

b) 分析该案例中公司的PR策略，确定其优点和不足之处。

c) 基于您的分析，提出一个改进该公司危机管理策略的建议。

4. 品牌建设a) 挑选一个知名消费品牌，研究其品牌价值和核心信息。

b) 分析该品牌的PR活动，如广告、赞助和社交媒体推广等。

c) 根据您的分析，提出一个借助公关手段来增强该品牌知名度和忠诚度的建议。

5. 事件策划a) 想象您正在策划一次大型活动，如产品发布会或慈善活动。

b) 描述您的活动目标、目标受众和关键信息。

c) 开发一个完整的事件策划方案，包括日程安排、媒体邀请和宣传计划。

6. 内容创作a) 选择一个关于您行业的热门主题。

b) 撰写一篇博客文章或新闻稿，深入探讨这个主题，并提供相关的见解和建议。

c) 分享您的创作，将其发布在适当的社交媒体平台上，并跟踪文章的表现。

这些PR练习题涵盖了公关工作的不同方面，帮助您在实践中提高专业能力。

通过解决这些题目，并与同事或导师进行讨论，您将加深对公关策略和实践的理解，进一步提升自己在公关领域的竞争力。

pr基础复习题公关(PR)是一种重要的沟通工具，它帮助组织与公众建立联系，并通过有效的传播策略来塑造和维护良好的形象。

为了掌握PR的基本知识和技巧，复习题是必不可少的。

在本文中，我们将回顾一些PR的基础复习题，以便更好地理解和应用这一领域的知识。

1. PR的定义是什么？PR是公关的简称，是Public Relations的缩写。

它是一种通过建立和维护组织与公众之间的良好关系，以及通过有效的传播策略来塑造和维护组织形象的沟通工具。

2. PR的目标是什么？PR的目标是建立和维护组织与公众之间的良好关系，以及塑造和维护组织的形象。

通过有效的传播策略，PR可以增加公众对组织的认知和理解，提高组织的声誉和信任度。

3. PR的原则有哪些？PR的原则包括真实性、透明度、一致性和可信度。

真实性指的是PR活动必须基于真实的信息和事实，不能夸大或歪曲事实。

透明度指的是PR活动应该公开透明，不隐藏信息或隐瞒真相。

一致性指的是PR活动应该与组织的价值观和行为保持一致，不产生矛盾。

可信度指的是PR活动应该建立在公众对组织的信任基础上，通过诚实、可靠和负责任的行为来增加公众的信任度。

4. PR的工具和技巧有哪些？PR的工具和技巧包括媒体关系、危机管理、社交媒体、品牌建设和事件营销等。

媒体关系是通过与媒体建立良好的合作关系，利用媒体的力量传播组织的信息和故事。

危机管理是在危机发生时，通过有效的沟通和处理策略来减轻危机对组织形象的负面影响。

社交媒体是通过利用各种社交媒体平台，与公众进行互动和传播信息。

品牌建设是通过塑造和传播组织的品牌形象，提高公众对组织的认知和好感度。

事件营销是通过组织和参与各种活动和事件，来增加公众对组织的关注和兴趣。

5. PR的成功案例有哪些？PR的成功案例有很多，例如可口可乐的“开心共享”活动，通过与公众分享快乐和正能量，提高了品牌形象和声誉。

另一个例子是红十字会在自然灾害和人道主义援助中的积极参与，通过有效的PR策略，增加了公众对该组织的信任和支持。

第一章1.连续图像中，图像为一个二维平面，(x,y)图像中的任意一点，f（x,y）为图像于(x,y)于处的值。

连续图像中，(x,y)的取值是连续的，f(x,y)也是连续的数字图像中，图像为一个由有限行有限列组成的二维平面，（i,j)为平面中的任意一点，g（i,j)则为图像在（i,j)处的灰度值，数字图像中，（i,j) 的取值是不连续的，只能取整数，对应第i行j列,g（i,j) 也是不连续的，表示图像i行j列处图像灰度值。

联系：数字图像g(i,j)是对连续图像f(x,y)经过采样和量化这两个步骤得到的。

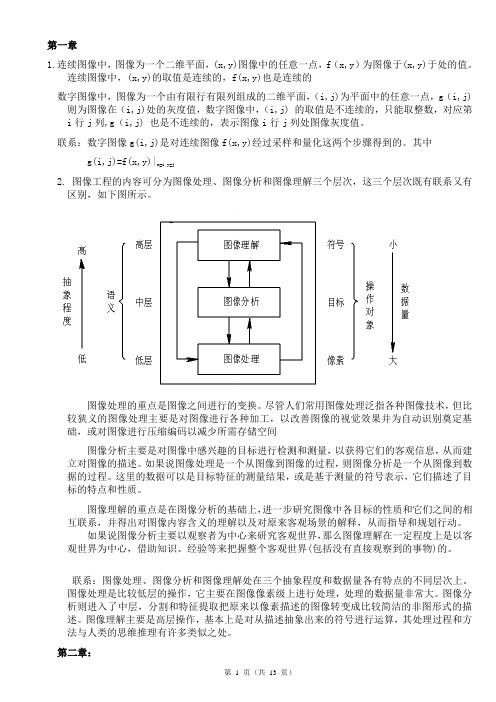
其中g(i,j)=f(x,y)|x=i,y=j2. 图像工程的内容可分为图像处理、图像分析和图像理解三个层次，这三个层次既有联系又有区别，如下图所示。

图像处理的重点是图像之间进行的变换。

尽管人们常用图像处理泛指各种图像技术，但比较狭义的图像处理主要是对图像进行各种加工，以改善图像的视觉效果并为自动识别奠定基础，或对图像进行压缩编码以减少所需存储空间图像分析主要是对图像中感兴趣的目标进行检测和测量，以获得它们的客观信息，从而建立对图像的描述。

如果说图像处理是一个从图像到图像的过程，则图像分析是一个从图像到数据的过程。

这里的数据可以是目标特征的测量结果，或是基于测量的符号表示，它们描述了目标的特点和性质。

图像理解的重点是在图像分析的基础上，进一步研究图像中各目标的性质和它们之间的相互联系，并得出对图像内容含义的理解以及对原来客观场景的解释，从而指导和规划行动。

如果说图像分析主要以观察者为中心来研究客观世界，那么图像理解在一定程度上是以客观世界为中心，借助知识、经验等来把握整个客观世界(包括没有直接观察到的事物)的。

联系：图像处理、图像分析和图像理解处在三个抽象程度和数据量各有特点的不同层次上。

图像处理是比较低层的操作，它主要在图像像素级上进行处理，处理的数据量非常大。

图像分析则进入了中层，分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式的描述。

用心辅导中心 高二数学三角函数知识点梳理:⒈L 弧长=αR=nπR 180 S 扇=21L R=21R 2α=3602R n ⋅π⒉正弦定理：A asin =B b sin =Cc sin = 2R （R 为三角形外接圆半径）⒊余弦定理：a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cosc 2=a 2+b2-2ab C cos bca cb A 2cos 222-+=⒋S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin=A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr =))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)⒌同角关系：⑴商的关系：①θtg =x y =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅===y x ctg ③θθθtg ry⋅==cos sin ④θθθθcsc cos 1sec ⋅===tg x r ⑤θθθctg rx⋅==sin cos ⑥θθθθsec sin 1csc ⋅===ctg y r ⑵倒数关系：1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg ⑶平方关系：1csc sec cos sin 222222=-=-=+θθθθθθctg tg ⑷)sin(cos sin 22ϕθθθ++=+b a b a（其中辅助角ϕ与点（a,b ）在同一象限，且ab tg =ϕ）⒍函数y=++⋅)sin(ϕωx A k 的图象及性质：（0,0>>A ω） 振幅A ，周期T =ωπ2, 频率f =T1, 相位ϕω+⋅x ，初相ϕ⒎五点作图法：令ϕω+x 依次为ππππ2,23,,20 求出x 与y ， 依点()y x ,作图 ⒏诱导公试 三角函数值等于α的同名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号；即：函数名不变，符号看象限三角函数值等于α的异名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号;即：函数名改变，符号看象限⒐和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos(μ=± ③βαβαβαtg tg tg tg tg ⋅±=±μ1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±μ⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++Ctg B tg C tg A tg B tgA tg⒑二倍角公式：(含万能公式) ①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-=③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=⒒三倍角公式：①)60sin()60sin(sin 4sin 4sin 33sin 3θθθθθθ+︒-︒=-= ②)60cos()60cos(cos 4cos 4cos 33cos 3θθθθθθ+︒-︒=+-=③)60()60(313323θθθθθθθ+⋅-⋅=--=tg tg tg tg tg tg tg ⒓半角公式：（符号的选择由2θ所在的象限确定） ①2cos 12sin θθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg⒔积化和差公式：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=()[]βαβαβα--+-=cos )cos(21sin sin ⒕和差化积公式： ①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos2cos2cos cos βαβαβα-+=+ ④2sin2sin2cos cos βαβαβα-+-=-例题：1．已知x ∈(－π2 ，0)，cos x ＝45 ，则tan2x 等于 （ ）A. 724B.－724C. 247D.－2472．3 cos π12 －sin π12 的值是 （ ）A.0B.－ 2C.2D.23．已知α，β均为锐角，且sin α＝55，cos β＝31010，则α＋β的值为 （ ）A. π4 或3π4B. 3π4C. π4D.2kπ＋π4 (k ∈Z )4．sin15°cos30°sin75°的值等于 （ ）A. 34B. 38C. 18D. 145．若f (cos x )＝cos2x ，则f (sin π12 )等于 （ ）A. 12B.－12C.－32D. 326．sin(x ＋60°)＋2sin(x －60°)－ 3 cos(120°－x )的值为 （ ）A. 12B. 32 C.1D.07．已知sin α＋cos α＝13 ，α∈(0，π)，那么sin2α，cos2α的值分别为 （ ）A. 89 ，179 B.－89 ，179C.－89 ，－179D.－89 ，±1798．在△ABC 中，若tan A tan B >1，则△ABC 的形状是 （ ）A.锐角三角形B.钝角三角形C.直角三角形D.不能确定9．化简cos （π4 ＋α）－sin （π4 ＋α）cos （π4 －α）＋sin （π4 －α）的结果为 （ ） A.tan αB.－tan αC.cot αD.－cot α10．已知sin α＋sin β＋sinγ＝0，cos α＋cos β＋co sγ＝0，则cos(α－β)的值为 （ ）A.－12B. 12 C.－1D.1二、填空题（本大题共6小题，每小题5分，共30分） 11．sin70＋cos150sin80cos70－sin150sin80 的值等于_____________.12．若1－tan A 1＋tan A ＝4＋ 5 ，则cot( π4 ＋A )＝_____________.13．已知tan x ＝43 (π＜x ＜2π)，则cos(2x －π3 )cos(π3 －x )－sin(2x －π3 )sin(π3 －x )＝_____.14．sin(π4 －3x )cos(π3 －3x )－cos(π6 ＋3x )sin(π4 ＋3x )＝_____________.15．已知tan(α＋β)＝25 ，tan(β－π4 )＝14 ，则sin(α＋π4 )·sin(π4 －α)的值为____________.16．已知5cos(α－β2 )＋7cos β2 ＝0，则tan α－β2 tan α2 ＝_____________.1．下列函数中，最小正周期为π的偶函数是 （ ）A.y ＝sin2xB.y ＝cos x2C.y ＝sin2x ＋cos2xD.y ＝1－tan 2x 1＋tan 2x2．设函数y ＝cos(sin x )，则 （ ）A.它的定义域是［－1，1］B.它是偶函数C.它的值域是［－cos1，cos1］D.它不是周期函数3．把函数y ＝cos x 的图象上的所有点的横坐标缩小到原来的一半，纵坐标扩大到原来的两倍，然后把图象向左平移π4 个单位.则所得图象表示的函数的解析式为 （ ）A.y ＝2sin2xB.y ＝－2sin2xC.y ＝2cos(2x ＋π4 )D.y ＝2cos(x 2 ＋π4 )4．函数y ＝2sin(3x －π4 )图象的两条相邻对称轴之间的距离是 （ ）A. π3B. 2π3 C.πD. 4π35．若sin α＋cos α＝m ，且－ 2 ≤m ＜－1，则α角所在象限是 （ ）A.第一象限B.第二象限C.第三象限D.第四象限17．已知cos(α－π6 )＝1213 ，π6 ＜α＜π2 ，求cos α.18．已知sin 22α＋sin2αcos α－cos2α＝1，α∈(0，π2 )，求sin α、tan α.19．在△ABC 中，已知A 、B 、C 成等差数列，求tan A 2 ＋tan C 2 ＋ 3 tan A 2 tan C2 的值.20．已知cos α＝－1213 ，cos(α＋β)＝17226，且α∈(π，32 π)，α＋β∈(32 π，2π)，求β.。

习题四1．用叠加定理求图题4-1所示电路中的电流i R 。

图题4-1解： A 2电流源单独作用时：A i R 12101010'−=×+−=V 80电压源单独作用时：i A i R 4101080''=+=原电路的解为：A i i i R R R 341'''=+−=+=2．用叠加定理求图题4-2所示电路中的电压u ab 。

4图题4-2解：V 24电压源单独作用时：Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时：Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为：V u u u ab ab ab 18612'''=+=+=3．用叠加定理求图题4-3所示电路中的电流i 。

6A图题4-3解： A 6电流源单独作用时：ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时：Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为：()()A i i i 624'''−=−+−=+=4．图题4-4所示电路中，R =6Ω，求R 消耗的功率。

图题4-4解： 将R 支路以外的部分看作一个二端电路。

可采用叠加原理求oc u ：12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻：eqRΩ=++×=426363eq R 原电路简化为：Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5．图题4-5所示电路中， R 1=1.5Ω R 2=2Ω，求（a ）从a、b 端看进去的等效电阻；（b ）i 1与i s 的函数关系。

pr制作练习题PR（Public Relations，公共关系）是一种重要的传播方式和管理策略，它与企业形象塑造、品牌推广等密切相关。

在现代社会中，PR在各行各业中的应用越来越广泛。

本文将通过制作练习题的形式，深入探讨PR的相关知识和实践技巧。

一、选择题1. 以下哪项不是PR的核心任务？a) 客户关系管理b) 媒体关系建立c) 社会责任履行d) 营销策划与执行2. 对于企业而言，以下哪种情况不适合进行PR活动？a) 产品推出b) 负面新闻报道c) 员工培训d) 品牌升级3. PR中的"公众"指的是：a) 企业的股东b) 企业的管理层c) 与企业有直接关系的人群d) 与企业无直接关系的人群4. 下列哪个不是PR的传播渠道？a) 报纸b) 电视c) 广播d) 微博5. 以下哪项不是PR活动的评估指标？a) 媒体曝光度b) 客户满意度c) 销售额d) 社交媒体粉丝数二、填空题1. PR的目标之一是在_____中传递企业信息。

2. PR的基本原则之一是______。

3. 在PR活动中，______是有效的传播媒介之一。

4. 企业进行PR活动时，应注重与______的互动。

5. PR活动的成功与否可以通过多种指标进行______。

三、案例分析题某公司为了提高企业形象，计划进行一次PR活动，请你根据以下情况回答问题。

情况描述：某公司近期遭遇质量问题，导致消费者对其产品产生了一定的担忧。

公司希望通过一次PR活动改变消费者的认知，树立良好的企业形象。

1. 你认为该公司应采取哪些PR策略来应对此次危机？2. 请设计一个PR活动方案，包括主题、内容、传播渠道等要素。

3. 你预计此次PR活动的效果如何？为什么？四、创意答题题1. 请用一句话概括PR的核心价值是什么？2. 请发挥你的创意，设计一个创新的PR活动，并简要描述你的设计思路。

五、论述题PR在企业的发展中起到重要的推动作用，请论述PR对企业的意义和价值，并以实际案例进行支持。

pr教材习题答案
PR教材习题答案：如何提高公关技巧
公关是现代社会中非常重要的一门技能，它涉及到人际关系、沟通技巧和危机
处理能力等多个方面。

在PR教材中，有许多习题可以帮助我们提高公关技巧，下面就让我们来看一些常见的PR教材习题答案，以帮助我们更好地掌握这门
技能。

1. 请简要描述什么是公关？
公关是一种通过建立和维护组织与公众之间良好关系的活动。

它涉及到传播信息、塑造品牌形象和处理公众关注的问题等方面。

2. 你认为在公关活动中最重要的是什么？
在公关活动中，最重要的是建立信任和透明度。

只有当公众对组织有信任，并
且能够获得真实和准确的信息时，公关活动才能取得成功。

3. 举例说明一次成功的公关活动。

例如，某公司在产品推出时，通过举办发布会、发布新闻稿和与媒体进行沟通，成功地吸引了公众的注意，并且获得了良好的口碑。

4. 请列举一些提高公关技巧的方法。

提高公关技巧的方法包括加强沟通能力、学习危机处理技巧、建立良好的人际
关系、了解公众需求和利益等。

通过这些习题答案，我们可以更好地理解公关活动的重要性，以及提高公关技
巧的方法。

希望大家能够在日常生活和工作中，更加注重公关，提高自己的公
关技巧，从而取得更好的成就。

pr案例练习题在PR案例练习题中，我们将探讨公关活动中的一个实际案例，并分析该案例中采取的公关策略及其效果。

本文将以案例分析的方式展开，旨在帮助读者更好地理解公关活动的实际应用。

案例概述某公司推出了一款新型智能手表，希望通过公关活动提高产品知名度和销售量。

该公司决定通过一系列公关活动来实现这一目标。

公关策略1. 媒体发布会公司决定举办一场媒体发布会，以宣布新型智能手表的推出。

在发布会上，公司高层介绍了产品的特点和优势，并展示了手表的实际使用效果。

此外，公司还邀请了一位知名时尚博主作为特邀嘉宾，提升活动的影响力和吸引力。

2. 媒体关系建设除了媒体发布会，公司还积极与媒体建立稳固的关系。

公司的公关团队定期与各大媒体进行沟通，提供有关产品的最新信息和独家新闻，以便媒体能够及时报道。

3. 社交媒体营销公司针对年轻人群体的社交媒体网站，如微博、微信等展开了一系列营销活动。

公司邀请了一些知名网络红人进行产品推广，同时组织了线上抽奖活动和在线讨论会，吸引用户关注，并通过用户互动提升产品知名度。

4. 合作伙伴推广公司与一些知名品牌达成合作协议，在一些知名商场设立展示柜台，展示并销售新型智能手表。

此外，公司还在一些主要城市的商业区发布宣传海报，提醒消费者可以在附近的商场购买到该产品。

效果分析通过以上公关策略，该公司成功提高了新型智能手表的知名度和销售量。

具体表现在以下几个方面：1. 媒体报道媒体在发布会后积极报道了该款智能手表，报道内容对产品的特点、功能进行了详细介绍，增加了产品的曝光度。

一些媒体还对公司的公关团队和营销策略进行了赞扬，进一步提升了品牌形象。

2. 社交媒体反响通过社交媒体的营销活动，该公司成功引起了用户的广泛关注和参与。

抽奖活动和线上讨论会吸引了大量参与者，增加了用户对新型智能手表的认知和兴趣，进而促进了产品销售。

3. 合作伙伴推广与知名品牌的合作让该公司的产品得到了更多的展示和销售机会。

在商场的展示柜台吸引了很多消费者前来了解和购买产品。

第3章3.6原题：试解释为什么离散直方图均衡技术一般不能得到平坦的直方图？答：假设有一副图像，共有像素个数为n=MN（M行N列），像素灰度值取值范围为（0～255），那么该图像的灰度值的个数为L=256，为了提高图像的对比度，通常我们都希望像素的灰度值不要都局促到某一个狭窄的范围，也就是我们通常说的图像灰度值的动态分布小。

最好是在有效灰度值取值范围上，每个灰度值都有MN/L个像素，这个时候我们就可以得到一张对比度最理想的图像，也就是说像素的取值跨度大，像素灰度值的动态范围大。

因为直方图是PDF（概率密度函数）的近似，而且在处理中，不允许造成新的灰度级，所以在实际的直方图均衡应用中，很少见到完美平坦的直方图。

因此，直方图均衡技术不能保证直方图的均匀分布，但是却可以扩展直方图的分布范围，也就意味着在直方图上，偏向左的暗区和偏向右的亮区都有像素分布，只是不能保证每个灰度级上都有像素分布。

（百度答案：）由于离散图像的直方图也是离散的，其灰度累积分布函数是一个不减的阶梯函数。

如果映射后的图像仍然能取到所有灰度级，则不发生任何变化。

如果映射的灰度级小于256，变换后的直方图会有某些灰度级空缺。

即调整后灰度级的概率基本不能取得相同的值，故产生的直方图不完全平坦。

3.8原题：在某些应用中，将输入图像的直方图模型化为高斯概率密度函数效果会是比较好的，高斯概率密度函数为：其中m和σ分别是高斯概率密度函数的均值和标准差。

具体处理方法是将m和σ看成是给定图像的平均灰度级和对比度。

对于直方图均衡，您所用的变换函数是什么？答：直方图均衡变换函数的一般表达式如下：在回答这个问题时，有两点非常重要，需要学生表达清楚。

第一，这个表达式假定灰度值r只有正值，然而，高斯密度函数通常的取值范围是-∞～∞，认识到这点是非常重要的，认识到这点，学生才能以多种不同的方式来解决问题。

对于像标准差这样的假设，好的答案是，需要足够小，以便于当r为小于0时，在p r(r)曲线下的面积可以被忽略。