第二章_距离分类器PPT教学课件
- 格式:ppt
- 大小:195.00 KB
- 文档页数:31









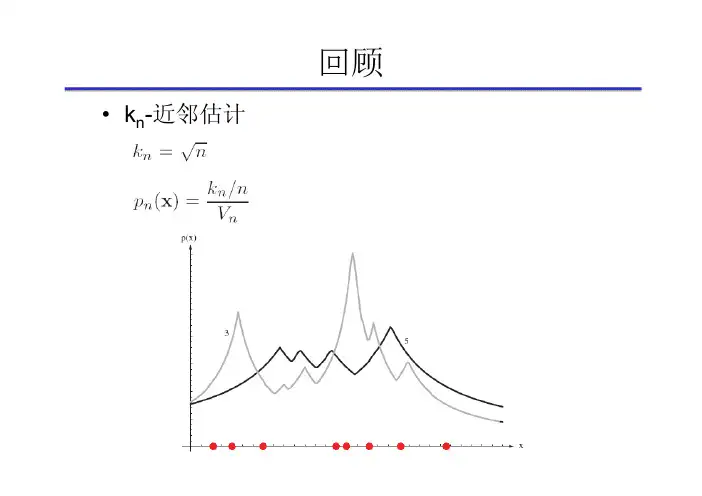
•k n-近邻估计•最近邻规则•直接估计后验概率•误差界如果x k 属于类别,则判断x 的类别为**12NN P e P ≤≤•k-近邻规则如果是在S中出现频率最高的类,则判断x的类别为•误差界•降低k-近邻计算复杂度的方法•计算部分距离•预建立结构•对训练样本加以剪辑Ch 05. 非参数方法Part 4 距离度量•最近邻规则或k-近邻规则以衡量模式(样本)之间的距离的度量为基础•距离度量是模式识别领域的核心问题之一•度量(metric)的一般化表示•度量必须满足的性质•非负性:•自反性:•对称性:•三角不等式:•d维空间中的欧几里德距离•特征尺度的变换会严重影响以欧几里德距离计算的近邻关系•解决方案•对每一个维度(特征)分布进行尺度均衡化,使得每一维上的变化范围都相等,如全部归一化成[0, 1]区间•d 维空间中的Minkowski 距离•又称为L k 范数•L 2范数——欧几里德距离•L 1范数——Manhattan 距离(街区距离)•范数——a 和b 在d 个坐标轴上投影距离的最大值11(,)di ii L a b ==-∑a b•到原点的等距离面•Mahalanobis 距离(马氏距离)在计算距离时考虑特征之间的协方差•Mahalanobis 距离与多元正态分布的关系1(,)()()t Mahalanobis D -=--a b a b Σa b Σ2(,)exp 2Manhalanobis D α⎡⎤=-⎢⎥⎣⎦x μ•例子•a :[0.8, 0.2]t ,b :[0.1, 0.5]t 从正态分布抽取,其中,求a 和b 之间的马氏距离•解:(0,)N Σ0.2000.1⎡⎤=⎢⎥⎣⎦Σ11(,)()()0.80.10.200.80.10.20.500.10.20.50.71/0.200.70.301/0.10t Mahalanobist t D --=--⎛⎫⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤ =-- ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭⎡⎤⎡⎤ =⎢⎥⎢⎥--⎣⎦⎣⎦a b a b Σa b 2222.30.7(0.3)0.7(0.3) 1.830.20.10.20.1⎡⎤⎢⎥⎣⎦-- =+=+=•Tanimoto 距离•n 1,n 2分别为集合S 1和S 2中的元素个数•n 12为两个集合交集中的元素个数•应用场景•两个模式(特征)之间要么相同,要么不同,无法计算某种分级的相似度•例如两个单词之间的Tanimoto 距离,可以将每个单词看作一个字母的集合•Tanimoto 距离•例子根据Tanimoto 距离,判断下列单词中哪个与‘pat’最为接近:‘cat’,‘pots’,‘pattern’•解所以‘cat’与‘pat’最为接近3422('','')0.6342Tanimoto D pat pots +-⨯==+-3322('','')0.5332Tanimoto D pat cat +-⨯==+-3723('','')0.57373Tanimoto D pat pattern +-⨯==+-•Hausdorff 距离•“一个集合中的点到另一个集合中的点的最小距离的最大值”•为某种衡量两点a 和b 之间距离的度量•欧几里德距离•Manhattan 距离•Mahalanobis 距离•……()(,)max max min (,),max min (,)Hausdorff b B a A a A b B D A B d a b d a b ∈∈∈∈= (,)d a b•Hausdorff 距离•例子计算集合与之间的Hausdorff 距离•解0.10.3,0.20.8A ⎧⎫⎡⎤⎡⎤=⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭0.50.7,0.50.3B ⎧⎫⎡⎤⎡⎤=⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭11(,)0.5d a b =12(,)0.61d a b =21(,)0.36d a b =22(,)0.64d a b =()(,)max max min (,),max min (,)max(max(0.5,0.36),max(0.36,0.61))max(0.5,0.61)0.61Hausdorff b B a A a A b B D A B d a b d a b ∈∈∈∈= = ==•Hausdorff 距离•练习计算集合与之间的Hausdorff 距离59,32A ⎧⎫-⎡⎤⎡⎤=⎨⎬⎢⎥⎢⎥-⎣⎦⎣⎦⎩⎭10,14B ⎧⎫⎡⎤⎡⎤=⎨⎬⎢⎥⎢⎥-⎣⎦⎣⎦⎩⎭Ch 06.特征降维和选择Part 1 特征降维-PCA•在实际应用中•当特征个数增加到某一个临界点后,继续增加反而会导致分类器的性能变差——“维度灾难”(curse ofdimensionality)•原因?•假设的概率模型与真实模型不匹配•训练样本个数有限,导致概率分布的估计不准•……•对于高维数据,“维度灾难”使解决模式识别问题非常困难,此时,往往要求首先降低特征向量的维度•降低特征向量维度的可行性特征向量往往是包含冗余信息的!•有些特征可能与分类问题无关•特征之间存在着很强的相关性•降低维度的方法•特征组合把几个特征组合在一起,形成新的特征•特征选择选择现有特征集的一个子集•降维问题•线性变换vs. 非线性变换•利用类别标签(有监督)vs. 不用类别标签(无监督)•不同的训练目标•最小化重构误差(主成分分析,PCA)•最大化类别可分性(线性判别分析,LDA)•最小化分类误差(判别训练,discriminative training)•保留最多细节的投影(投影寻踪,projection pursuit)•最大限度的使各特征之间独立(独立成分分析,ICA)•用一维向量表示d 维样本•用通过样本均值m 的直线(单位向量为e )上的点表示样本•最小化平方重构误差()tk k a =-e x m ˆk k a =+xm e 221111222111(,,,)()(())2()nnn k k k k k k nn ntkk k k k k k J a a a a a a ======+-=-- =--+-∑∑∑∑∑e m e x e x m e e x m x mkx 唯一决定了k a ˆkx11(,,,)22()0tn k k kJ a a a a ∂=--=∂e e x m (x k -m)在e 上的投影•用一维向量表示d维样本eak xkm•寻找e 的最优方向()tk k a =-e x m 22211111(,,,)2()nn ntn kk k k k k k J a a a a ====--+-∑∑∑e e e x m x m2221111221121121()2[()]()()nnnkkk k k k nntk k k k nnttk k k k k ntk k J a a =========-+- =--+- =---+- =-+-∑∑∑∑∑∑∑∑e x me x m x me x m x m e x me Se x m1()()nt k k k ==--∑S x m x m 散布矩阵(scatter matrix )(1)n C=-•使最小的e 最大化•拉格朗日乘子法(约束条件)•结论:e 为散布矩阵最大的本征值对应的本征向量(1)t tu λ=--e Se e e 1()J e te Se220uλ∂=-=∂Se e e1t =e e λ=Se e是S 的本征值(eigenvalue )e 是S 的本征向量(eigenvector )λt t λλ==e Se e e 最大本征值对应的最大值λt e Se•将一维的扩展到维空间•用来表示•最小化平方误差1ˆd k ki i i a '==+∑xm e k a ()d d d '' ≤12k k k kd a a a '⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦y k x 211()nd d ki i kk i J a ''==⎛⎫=+- ⎪⎝⎭∑∑e m e x•将一维的扩展到维空间•结论:•使得平方误差最小的向量分别为散布矩阵S 的个最大本征值对应的本征向量•S 为实对称矩阵,所以相互正交•可被视为特征空间的一个子空间的单位向量基•为对应于基的系数,或在上的投影•称为主成分(principal component )•几何意义为沿数据云团方差最大的方向的直线•利用PCA ,可以将d 维数据降维到维,同时使得降维后的数据与源数据的平方误差最小k a ()d d d '' ≤12,,d 'e e e d '12,,d 'e e e 12,,d 'e e e ki a k x i e i e ki a 12,,d 'e e e ()d d d '' ≤•主成分分析步骤(d 维降为维)1.计算散布矩阵S2.计算S 的本征值和本证向量3.将本征向量按相应的本征值从大到小排序4.选择最大的d’个本征向量作为投影向量,构成投影矩阵W ,其中第i 列为5.对任意d 维样本x ,其用PCA 降维后的d’维向量为()d d d '' ≤1()()ntk k k ==--∑S x m x m λ=Se e12,,d 'e e e i e t=y W x'd d ⨯•通常,最大的几个本征值占据了所有本征值之和的绝大部分•少数几个最大本征值对应的本证向量即可表示原数据中的绝大部分信息,而剩下的小部分(即对应较小的本征值的本征向量所表示的信息),通常可以认为是数据噪声而丢掉•原维度:4用PCA降到2维用PCA降到3维•PCA 中对散布矩阵S 的本征值分解计算量较大,如特征向量维度较高,直接对S 进行本征值分解十分困难。