第1章 点、直线、平面的投影
- 格式:doc
- 大小:1.57 MB
- 文档页数:23

一、点、直线、平面的投影1.1 点的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第24~24页习题1.2 直线的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第25~27页习题1.3 平面的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第28~29页习题1.4 直线与平面、平面与平面相对关系∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第30~32页习题1234题号:题号:56789101112131415题号:161718192021题号:2223242526272829303132333435363738391.5 换面法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第33~35页习题1.6 旋转法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第36~36页习题1.7 投影变换综合题∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第37~37页习题点、直线、平面的投影题号:404142434445464748495051题号:525354555657题号:58596061621. 已知A、B、C三点的直观图,画出它们的投影图,并将各点的坐标值填入表中。
2. 已知A、B、C各点对投影面的距离,画出它们的三面投影图和直观图。
3. 已知点A的坐标(40,15,0),画出其三面投影并作出点B和点C的三面投影。
(a)点B ——在点A右面20mm,前面15mm,上面20mm;(b)点C ——在点A左面10mm,后面15mm,上面15mm。

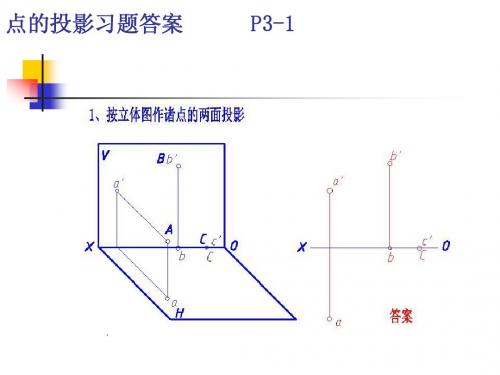


第一部分点与直线一、已知各点的空间位置,画出其投影图(尺寸由立体图量取,并取整)。
知识点:点的投影规律1、1、点的投影规律(一般点、投影轴上点、投影面内点)——高平齐(Z);长对正(X);宽相等(Y)(相对原点)。
2、2、立体图的画法(轴向测量;轴向平行作图法——各线都分别平行于轴线)3、3、答案见下图:二、已知点的一个投影和下列条件,求其余两个投影。
(1)(1) A点与V面的距离为20mm。
(2) B点在A点的左方10mm。
知识点:1、点的投影规律(一般点、投影轴上点、投影面内点)——高平齐(Z);长对正(X);宽相等(Y)(相对原点)。
2、立体图的画法(轴向测量;轴向平行作图法——各线都分别平行于轴线)3、答案见下图:三、已知点A(35、20、20),B(15、0、25),求作它们的投影图。
答案见下图:四、已知各点的两个投影,求作出第三投影。
答案见下图:五、判断下列各点的相对位置。
知识点:点的相对位置(X—大左小右;Y—大前小后;Z—大上小下);坐标的量取。
答案见下图:六、已知点B在点A的左方10mm,下方15mm,前方10mm;点C在点D的正前方10mm,作出点B和点C的三面投影。
答案见下图:七、已知A点(10,10,15);点B距离投投影面W、V、H分别为20、15、5;点C在点A左方10,前方10,上方5,作出A、B、C的三面投影。
答案见下图:距离相等,点B的三个坐标值有什么关系,作出点B的各投影。
知识点:1、点的投影规律:高平齐(Z );长对正(X );宽相等(Y )(相对原点)——点到H 、V 、W 面的距离分别为:Z 、Y 、X 。
2、若点B 到H 、V 、W 面的距离相等,则:Z b =Y b =X b 。
2、答案见下图:九、判断下列各直线对投影面的相对位置,并画出三面投影。
答案见下图:个解)。
答案见下图:十一、求线段AB的实长及其与H、V面的倾角α、β知识点:直角三角形法求直线的倾角及线段实长。

第1章 点、直线、平面的投影在生产实际中,设计和制造部门普遍使用图样来表达物体。
工程图样是利用投影的方法获得的。
本章介绍投影的一些基本知识以及点、直线、平面的投影规律和作图方法。
1.1投影法的基本知识由光的投射成影这一物理现象,人们创造了用投影来表达物体形状的方法——投影法。
由国家标准(GB/T16948)定义:投射线经过物体,向选定的面投射,在该面上得到图形的方法称为投影法。
从图1-1可知,投射线、被投射物和投影平面是进行投射时不可缺少的条件,称投影三要素。
在表示投影的图样中,空间几何元素用大写字母(斜体)表示,而投影用同名小写字母表示。
P图1-1投影三要素 图1-2中心投影法1.1.1中心投影法投射线都从投射中心出发的投影法称为中心投影法。
如图1-2所示,通过投射中心S 作出△ABC 在投影面P 上的投影:投射线SA 、SB 、SC 分别与投影面交于a 、b 、c ,直线ab 、bc 、ca 分别是直线AB 、BC 、CA 的投影,而△ABC 的投影就是△abc 。
中心投影法主要用于建筑物或产品的立体图。
以中心投影法为依据所作的投影称透视投影。
由于透视投影所画的图形符合于视觉印象,空间立体感强,形象生动逼真,所以广泛用于科学、艺术和工程技术等领域。
用透视投影所画得的图形,也称透视图。
1.1.2平行投影法若投射中心S 移到无穷远处,投射线相互平行,称平行投影法,所得投影称平行投影。
平行投影法又分正投影法和斜投影法:投射方向(即投射线的方向)垂直于投影面的是正投影法,如图1-3(a ),投射方向倾斜于投影面的是斜投影法,如图1-3(b )。
由于正投影图的作图较其他图视法简便,又便于度量,在工程上得到广泛应用,机械图样主要是用正投影法绘制。
为叙述简单,今后将“正投影”简称“投影”。
(a )正投影法(b )斜投影法图1-3平行投影法平行投影有下述若干投影特性:(1)实形性:与投影面平行的物体,如平面、直线,投射后所得投影反映该物体的实形,如图1-4(a )所示;(2)积聚性:与投射线平行的平面或直线,投射后所得投影积聚为直线或点,如图1-4(b )所示;(3)从属性:直线上的点或平面上的点和线,投射后所得投影仍在直线或平面的投影上,如图1-4(c )所示;(4)等比性:点分线段所成的比例,投影后不变,如图1-4(d )所示,ac :cb =AC :CB 。
(d)等比性(c)从属性 (b )积聚性(a)实形性图1-4平行投影特性1.1.3投影体系如图1-5所示,由空间点A 向平面P 作正投射,得惟一的投影a 。
反之,若已知点B 的投影b ,就不能惟一确定点B 的空间位置。
换句话说,一个投影无法描述一个物体。
因此,常把几何形体放在相互垂直的两个或三个投影面之间,并在这些投影面上形成多面投影。
如图1-6(a )所示,设立相互垂直的正立投影面V (简称正面)和水平投影面H ,组成两投影面体系,将空间划分为四个角:第一角、第二角、第三角和第四角,V 面和H 面交于投影轴(两投影面的交线)OX 。
如图1-6(b )所示,再设立一个与V 面、H 面都垂直的侧立投影面W (简称侧面),组成三投影面体系,将空间划分为八个角,每两个投影面的交线,形成OX 、OY 和OZ 三根投影轴,且互相垂直。
无论是两面体系、三面体系,本书着重讲述第一角中的几何形体的投影。
(b)三投影面体系(a)两投影面体系图1-5点的一个投影图1-6投影体系1.2点的投影1.2.1点的两面投影和三面投影1.点的两面投影如图1-7(a)所示,由空间点A作垂直于V面、H面的投射线Aa′、Aa,分别与V面、H 面交得点A的正面投影(V面投影)a′和水平投影(H面投影)a。
为区分空间点和投影点,我们规定:空间点用大写(斜体)字母表示,如A、B、C……,H面上的投影点用小写字母表示,如a、b、c……,V面上的投影点用小写字母加一撇表示,如a′、b′、c′……。
由于平面Aa′a分别垂直于H面、V面,则平面Aa′a⊥OX轴并交于a x点,因此a′a x⊥OX,aa x⊥OX。
又因四边形Aaa x a′是矩形,所以a x a′=aA,反映点A到面H的距离;a x a=a′A,反映点A到V面的距离。
V面保持不动,将H面绕OX轴向下旋转90°,与V面展成一个平面,如图1-7(b)所示。
展开后,a′a形成一条投影连线(交OX轴于a x点),且a′a垂直于OX轴。
在实际画图时,不必画出投影面的边框和点a x,图1-7(c)即为点A的投影图。
(c)点的投影图(b)投影面展开后(a)直观图a Xa′VaO Oa′X X图1-7点在两面体系中的投影由此可概括出点的两面投影特性:(1) 点的投影连线垂直于投影轴,即a′a ⊥OX ;(2) 点的投影与投影轴的距离,反映点与投影面的距离,即a x a ′反映点到H 面的距离,a x a 反映点到V 面的距离。
已知一点的两面投影,就可惟一地确定该点的空间位置。
读者自行想象:若将图1-7(c ),中OX 轴以下的H 面自前向上抬起90°,由a 作H 面的垂线,由a ′ 作V 面的垂线,两垂线的交点,即空间点A 的惟一位置。
2.点的三面投影三面体系第一角如图1-8所示,其展开的方法是V 面不动,H 面绕OX 轴自前向下,W 面绕OZ 轴自前向右各转90°后与V 面重合,OY 轴则分为H 面上的OY H 和W 面上的OY W ,如图1-8(b )。
XOY HZY W(a )直观图(b )投影图(b)点的投影图(a)直观图OX Y H aa ′ a ″ Y W图1-8三面体系第一角 图1-9点的三面投影如图1-9(a )所示,由空间点A 分别作垂直于V 面、H 面、W 面的投射线,交得点A 的正面投影a ′、水平投影a 和侧面投影a ″(W 面投影,规定用小写字母加两撇表示)。
与两面体系中一样,每两条投射线确定一个平面,分别垂直投影轴。
展开后就得如图1-9(b )所示的投影图,且a ′a ⊥OX ,a ′a ″⊥OZ ,aa Y H ⊥OY H ,a ″a Y w ⊥OY W ,Oa Y H =Oa Y W 。
为保证a ″ 点的作图准确,即保证Oa Y H =Oa Y W ,可过O 点作一45°斜线,aa Y H 和a ″a Y w 的延长线必与该斜线交于一点,由此定出a ″(或a )。
由上分析,得出点的三面投影特性:(1)点的投影连线垂直于相应的投影轴,即a ′a ⊥OX ,a ′a ″⊥OZ ,aa ″⊥OY (投影图中表现为aa Y H ⊥OY H ,a ″a Y w ⊥OY W );(2) 点的投影与投影轴的距离,反映点与投影面的距离,即a ′a x (或a ″a Y w )反映点到H 面的距离,aa x (或a ″a Z )反映点到V 面的距离,aa Y H (或a ′a Z )反映点到W 面的距离。
利用点的两投影,就可求得第三个投影。
1.2.2点的投影与该点直角坐标的关系如图1-10所示,若将三面体系看做直角坐标系,则投影轴、投影面、点O 分别是坐标轴、坐标面、原点。
点A (x A ,y A ,z A )的投影与该点的坐标有下述关系:X 坐标x A (即Oa x )=a z a ′=a Y H a =点A 到W 面距离a ″A ;Y 坐标y A (即Oa Y H =Oa Y W )=a X a =a Z a ″=点A 到V 面距离a ′A ; Z 坐标z A (即Oa Z )=a X a ′=a Y W a ″=点A 到H 面距离aA 。
点的一个投影可以反映空间点的两个坐标,因此,当空间点A 由坐标(x ,y ,z )给定后,就可作出点A 的三个投影;反之,亦然。
(b)投影图(a)直观图H Wb'b' d' d"b dOY HX(b)点的投影图(a)直观图Zc"Y W图1-10点的投影与该点直角坐标的对应关系 图1-11投影面和投影轴上的点图1-11是位于V 面、H 面和OX 轴上的三点B 、C 、D 的直观图和投影图,由图可看出其坐标和投影具有下述特征:(1)投影面上的点有一个坐标为零,在该投影面上的投影与其空间点重合,其他两投影分别在相应的投影轴上(如点B 点C )。
(2)投影轴上的点有两个坐标为零,在该轴上有两个投影与其空间点重合,其余的一个投影落在原点O 上(如点D )。
【例】已知点A 的坐标为(15,10,20),点B 的坐标为(20,0,10),点C 的坐标为(0,15,0),分别求A 、B 、C 三点的投影图。
〖解〗步骤如下:(1) 画两条互相垂直的细实线作为投影轴,标上相应的字母,再作一条成45°的细实线为作图辅助线;(2) 从原点出发,沿OX 轴向左量取15mm 得一点,定为a X ,过该点作OX 轴的垂线(如图1-12(a )所示);(3) 在该垂线上,从a X 出发向上量取20mm 得一点,定为a ′,向下量取10mm 得一点,定为a (如图1-12(b )所示); (4) 由点A 的两投影(a ,a ′),用“二求三”的方法作图即可得点A 的第三投影a ″(如图1-12(c )所示)。
B 、C两点的作图过程与点A 类似,见图1-12(d )。
(d)(c) (a)(b)W Wa'a"b" b' b aXOY H c' c图1-12由给定的点的坐标值求点的投影图1.2.3两点的相对位置及重影点空间两点的相对位置是指它们的左右、前后及上下之间的关系,一般由X 、Y 、Z 三个方向上的坐标差来判断。
如图1-13所示,因为x A >x B ,y A <y B ,z A <z B ,所以点A 在点B 的左、后、下方。
它们之间在这三个方向上的坐标差,即为这两点对投影面W 、V 、H 的距离差。
若已知两点的相对位置及其中一个点的投影,就能作出另一个点的投影。
需要注意的是:对水平投影而言沿OY H 轴移动代表向前,而对侧面投影而言,沿OY W 轴移动也代表向前。
(a)直观图(b)投影图W图1-13两点相对位置当空间两点位于某一投影面的一条投射线上,则此两点在该面的投影必重合,称之为该投影面的重影点,如图1-14。
从相对位置分析,点C 在点A 之后y A -y C 处,因为x A =x C ,z A =z C ,所以点C 与点A 无左右距离差和上下距离差,点C 在点A 的正后方,正面投影相重合,点A 和点C 称为对正面的重影点。
(b)投影图(a)直观图c"Za'(c')Xc aY H Y Wa"图1-14重影点对V 面、H 面、W 面的重影点的可见性判断,分别应是前遮后、上遮下、左遮右。