第4讲.第二轮复习之函数图象上点的存在性问题中的距离、面积与角度.尖子班.学生版

中考数学专题复习——存在性问题存在性问题是指判断满足某种条件的事物是否存在的问题，这类问题的知识覆盖面较广，综合性较强，题意构思非常精巧，解题方法灵活，对学生分析问题和解决问题的能力要求较高，是近几年来包括深圳在内各地中考的“热点”。

这类题目解法的一般思路是：假设存在→推理论证→得出结论。

若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断。

以下为几种典型的二次函数中出现的存在性问题，讲解后希望各位考生在以后的考试中如果遇到此类型时能够很顺畅的把过程写下来。

一、二次函数中相似三角形的存在性问题1.（2011枣庄10分）如图，在平面直角坐标系xoy 中，把抛物线2y x =向左平移1个单位，再向下平移4个单位，得到抛物线2()y x h k =-+.所得抛物线与x 轴交于A ，B 两点（点A 在点B 的左边），与y 轴交于点C ，顶点为D. （1）写出h k 、的值；（2）判断△ACD 的形状，并说明理由；（3）在线段AC 上是否存在点M ，使△AOM ∽△ABC ？若存在，求出点M 的坐标；若不存在，说明理由.2.（2011临沂13分）如图，已知抛物线经过A （﹣2，0），B （﹣3，3）及原点O ，顶点为C ． （1）求抛物线的解析式；（2）若点D 在抛物线上，点E 在抛物线的对称轴上，且A 、O 、D 、E 为顶点的四边形是平行四边形，求点D 的坐标；（3）P 是抛物线上的第一象限内的动点，过点P 作PM ⊥x 轴，垂足为M ，是否存在点P ，使得以P 、M 、A 为顶点的三角形△BOC 相似？若存在，求出点P 的坐标；若不存在，请说明理由．二、二次函数中面积的存在性问题3. （2011日照10分）如图，抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ，B ．已知点B 的坐标为（－2，－2），点A 在第一象限内，且tan ∠AOX 错误!未找到引用源。

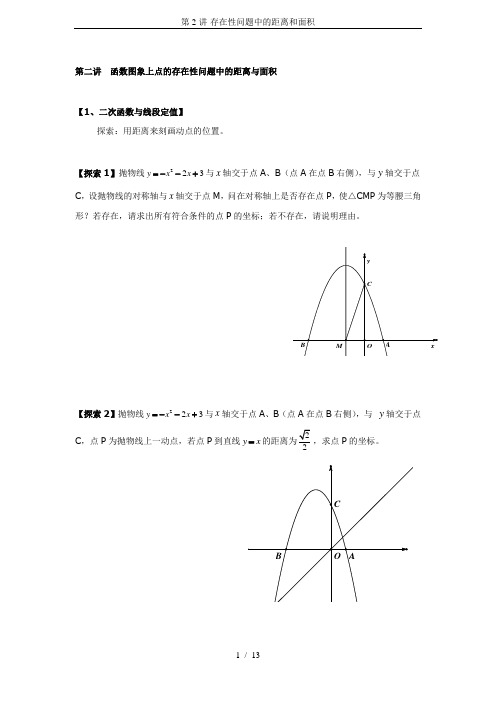
第二讲函数图象上点的存在性问题中的距离与面积【1、二次函数与线段定值】探索：用距离来刻画动点的位置。

【探索1】抛物线2=--y xC，设抛物线的对称轴与x Array【探索2】抛物线22y x=--C，点P【探索3】抛物线223=--+与xy x xC，点P为抛物线上一动点，若点P Array【探索4】抛物线223=--+与xy x x点P为抛物线上一动点，若点P【探索5】抛物线223=--+与xy x x点P为△BOC内一点，且点P到△BOC【2、线段最值问题补充】动点满足线段间大小关系、和差最值等。

中考主要考查以下两点： （1）“两点间线段最短” （2）“垂线段最短”（1）两点间线段最短 （下面按三大变换来分类） ※ 旋转型已知AB a =，AC b =，其中a b <，求BC 的最值。

※ 轴对称型1、在直线l 上找一点P ，使得其到直线同侧两点A 、B 的距离之和最小。

2、直线12l l 、交于O 、P 是两直线间的一点，在直线12l l 、上分别找一点A 、B ，使得△PAB的周长最短。

3、直线12l l 、交于O ，A 、B 是两直线间的两点，从点A 出发，先到1l 上一点P ，再从P 点到2l 上一点Q ，再回到B 点，求作P 、Q 两点，使四边形APQB 周长最小。

BlAB22※ 平移型1、从A 点出发，先移动到直线l 上的一点P ，再在l 上移动一段固定的距离PQ ，再回到点B ，求作点P ，使移动的距离最短。

2、A 、B 是位于河两岸的两个村庄，要在这条宽度为d 的河上垂直建一座桥，使得从A 村庄经过桥到B 村庄所走的路程最短。

（2）垂线段最短”ABAB【真题模拟】【例1】平面直角坐标系中，抛物线2y ax bx c =++的对称轴为2x =，且经过B （0，4）， C （5，9），直线BC 与x 轴交于点A 。

（1）求出直线BC 及抛物线的解析式。

（2）D （1，y M 在点N 的上方，使得四边形若不存在，请说明理由。

《函数图象中的点的存在性问题》（第 1 课时）教学设计一、内容和内容解析1.内容两类三角形在函数图象中的点的存在性问题.2.内容解析本节课设想定位在中考第二轮专题复习中进行. 针对等腰三角形和直角三角形在函数图象中涉及的点的存在性问题，通过引导学生针对不同类型的三角形的性质特点，归纳出常见的解答点的存在性问题的基本思路，感受分类思想，方程思想在此类问题中的运用. 等腰三角形主要运用对顶角顶点的位置选择的分类；直角三角形则主要根据直角顶点的位置选择进行分类. 分类思路比较自然合理，对于解答相关的点的存在性问题有很大的帮助.基于以上分析，本节课的教学重点是：两类三角形在函数图象中的点的存在性问题的分类方法.二、目标和目标解析1.教学目标（1）理解两类三角形在函数图象中的点的存在性问题的分类方法；（2）通过独立思考，动手操作，合作探究，体会分类、方程、建模等数学思想.2.目标解析达成（1）的标志是：能够运用两类三角形在函数图象中的点的存在性问题的分类方法解决相关问题.达成（2）的标志是：通过画图及对图形的观察、对问题的分析，能够运用分类讨论解决两类三角形在函数图象中的点的存在性问题.三、教学问题诊断分析两类三角形在函数图象中的点的存在性问题经常出现在解答题的压轴部分，有一定的抽象性. 其存在性对于学生的创造性思维有较高的要求. 同时，此类问题由于自身的开放性，往往存在一题多解. 因此，合理对问题进行分析并准确得出解答的所有可能性比较困难.本节课的教学难点是：分类讨论思想在点的存在性问题中的运用（按顶角顶点分类求等腰三角形，按直角顶点分类求直角三角形）.四、教学条件支持分析利用几何画板动态演示图形的变化过程，增强学生的几何直观，促使解答生成的自然合理.五、教学过程设计yCA BO1. 目标导入，明确任务 本节课的学习目标： （1） 理解两类三角形在函数图象中的点的存在性问题的分类方法； （2） 通过独立思考，动手操作，合作探究，体会分类、方程、建模等数学思想. 师生活动：教师 PPT 展示本节课的学习目标，学生大声朗读. 设计意图：通过朗读学习目标，学生能够明确本节课的学习任务.2. 复习热身，梳理知识课前任务：展示等腰三角形的性质，相似三角形的性质以及勾股定理组成的知识结构框 图.师生活动：学生展示课前完成的知识结构图，教学与学生一起进行点评，补充或纠正. 设计意图：通过回顾两类三角形的常用性质，做好课前热身，为课堂后续的学习讨论提 供知识储备，锻炼学生的自主归纳能力.3. 交流研讨，题串解疑问题 1（顶角顶点分类）．已知抛物线 y = - 3 x 2+ 3x + 3 经 8 4过 A （-2，0）、B （4，0）、C （0，3）三点. 在 y 轴上是否存在点 M ，使△ACM 为等腰三角形？若存在，请直接写出满足要求 x的点 M 的坐标；若不存在，请说明理由.解题思路：引导讨论：假设点 M 存在. 要确定点 M 的位置，关键是判断哪两条边为腰. 为了确定腰的位置，可以通过确定顶角来完成. 对于△ACM ： ①若点 A 为顶角顶点，此时可得相等的两腰为 = . 锦囊：如图 1，点 A 落在 CM 的垂直平分线上，利用对称性突破问题.②若点 C 为顶角顶点，此时可得相等的两腰为 =.锦囊：如图 2，点 C 落在坐标轴上，利用画圆找交点突破问题. 注意此处存在多解.y MC OA M'x③若点 M 为顶角顶点，此时可得相等的两腰为= .锦囊：如图 3，点 M 在 AC 垂直平分线与对应的 坐标轴的交点处，利用三角函数或相似突破问题.yCDMA O x图 1 图 2 图 3师生活动：教师动态展示图形的变化过程，学生小组研讨，组长组织本组成员核对答案，纠正或补充解题过程，教师巡堂，指导.解：假设点 M 存在.（1）如图 1，若点 A 为顶角顶点，此时可得，AC =AM . 易知点 M 与点 C 关于 x 轴对称. 因此，M （0，-3）.（2）如图 2，若点 C 为顶角顶点，此时可得，CA =CM . 因为 所以 M （0，3 + ）或 M’（0，3 − ）.（3）如图 3，若点 M 为顶角顶点， 可得，MA =MC . 取 AC 中点 D ，易得5综上所述，点 M 的坐标分别为（0，-3），（0，3 + ），（0，3 − ），（0， 6）. 总结追问：1. 本题中的分类依据是什么？ 2. 每种情况下的大致的解答思路是什么？3. 在上述的每种类别里，你还有其他的解答方法吗？设计意图及方法总结：通过问题串和几何画板展示，引导学生对腰的选择进行分类归结到顶角顶点分类. 得出对于给定的两个已知点，它们作为顶角的顶点时，通过画圆的方式容易确定动点的位置，再根据顶角顶点的不同位置选择不同方法突破；对于没给定的点 M ，通过画垂直平分线与坐标轴的交点的方法来确定位置，再根据勾股定理、三角函数或者相似的方法来突破. 最后通过追问和归纳，让学生形成此类分类问题的基本解题思路.变式 1 如图，在平面直角坐标系 xOy 中，已知点 D （3，4），点 P 是 x 轴正半轴上的一个动点，如果△DOP 是等腰三角形，求点 P 的坐标.（说明：本题只需做好基本分类，不需要写出详细的解答过程. 详细的解答过程作为课后作业独立完成. ）解题思路：y CAOxMyDOx解：假设点 P 存在. （1） 点 O 为顶角顶点. 此时，OD =OP . （2） 点 D 为顶角顶点. 此时，DO =DP . （3） 点 P 为顶角顶点. 此时，PO =PD .设计意图：通过变式，巩固根据顶角顶点进行分类讨论的基本思路，感受深化分类讨论的思想.三垂直模型：AB问题 2（ 直角顶点分类）. 如图，过点 C （ 0 ， 2 ）的抛物线1 3y = - x 2 + 2 2 x + 2 与直线 A D 交于 A （-1，0）、D （3，2）两点. 在 y轴上是否存在点 P 使得△PAD 是直角三角形？若存在，求出点 P 的坐标；若不存在，请说明理由.解题思路：引导讨论：假设点 P 存在. 要确定点 P 的位置，关键是判断哪两条边互相垂直. 为此， 可以通过确定哪个角作为直角来完成. 对于△PAD ： ① 若点 A 为直角顶点，此时可得，⊥.yC DA BOx锦囊：如图 4，过点A 作直线平行于y 轴，过点P、D，分别作直线平行于x 轴，构造出一个三垂直模型. 利用相似突破问题.②若点D 为直角顶点，此时可得，⊥.锦囊：如图 5，过点D 作直线平行于y 轴，过点P、A，分别作直线平行于x 轴，构造出一个三垂直模型. 利用相似突破问题.③若点P 为直角顶点，此时可得，⊥.锦囊：如图 6，过点P 作直线平行于x 轴，过点D、A，分别作直线平行于y 轴，构造出一个三垂直模型. 利用相似突破问题. 此类情况由于自身的特点，存在两个解，可通过画出以AD 为直径的圆来加深理解.师生活动：教师动态展示图形的变化过程，学生小组研讨，组长组织本组成员核对答案，纠正或补充解题过程，教师巡堂，指导.解：设点P 坐标为（0，y）.（1）如图 4，若点A 为直角顶点，此时可得，DA⊥AP. 过点A 作直线平行于y 轴，过点P、D，分别作直线平行于x 轴. 由相似可得，−y= 1. 解得y=-2. 所以，P（0，-2）.4 2（2）如图 5，若点D 为直角顶点，此时可得，PD⊥DA. 过点D 作直线平行于y 轴，过点P、A，分别作直线平行于x 轴. 由相似可得，3 = y−2.解得y=8. 所以，P（0，8）.2 4（3）如图 6，若点P 为直角顶点，此时可得，AP⊥PD. 过点P 作直线平行于x 轴，过点D、A，分别作直线平行于y 轴. 由相似可得， 1 = y.解得y=3 或y=-1. 所以，P（0，3）或P‘（0，-1）.y−2 3综上所述，点P 的坐标为（0，-2），（0，8），（0，3），（0，-1）.总结追问：1. 本题中的分类依据是什么？ 2. 每种情况下的大致的解答思路是什么？3.在上述的每种类别里，你还有其他的解答方法吗？比如，勾股定理能否应用在其中？如果能，它与相似法对比有什么优劣？设计意图及方法总结：通过问题串和几何画板动态展示，引导学生通过对直角边的选择进行分类归结到直角顶点的分类. 得出对于给定的点作为直角顶点时，通过过直角顶点作y 轴的平行线，过其余顶点作x 轴的平行线，构造三垂直模型，进而通过相似突破；对于未给定的点作为直角顶点时，通过过直角顶点作x 轴的平行线，过其余顶点作y 轴的平行线，构造三垂直模型，进而通过相似突破. 在整个过程中感受分类和建模的思想.变式2如图，抛物线y=-x2 +4x-3与x 轴交于A、B 两点（A 在B 的左边），与y 轴交于点 D . 在抛物线上是否存在一点 P ，使得△BDP 是直角三角形？ 若存在，请求出点 P 的坐标；若不存在，请说明理由.（说明：本题只需做好基本分类，不需要写出详细的解答过程. 详细的解答过程作为课后作业独立完成. ）解题思路：解：假设点 P 存在. （1） 点 B 为直角顶点. 此时，PB ⊥BD . （2） 点 D 为直角顶点. 此时，PD ⊥DB . （3） 点 P 为直角顶点. 此时，BP ⊥PD .设计意图：通过变式，巩固根据直角顶点进行分类讨论的基本思路，感受深化分类讨论的思想.4. 师生交流，捡拾收获请谈谈这节课你有什么收获？师生活动：教师与学生一起回顾本节课研究的内容.设计意图：引导学生总结两类三角形在函数图象中的点的存在性问题的分类方法和基本解题思路，提升学生综合运用知识的能力.5. 布置作业，活学活用独立完成变式 1、变式 2 的完整解答过程.设计意图：巩固本节课所学，加深对等腰三角形和直角三角形在函数图象中的点的存在性问题的分类方法和基本解题思路的理解.选题说明：本教学设计题目选自马学斌编著的华东师范大学出版社 2016 版的《挑战压轴题·中考数学·强化训练篇》. 为了重点突出点的存在性问题的讨论，在尽量保留二次函数背景的前提下，弱化了原题在二次函数解析式求解上的考察。

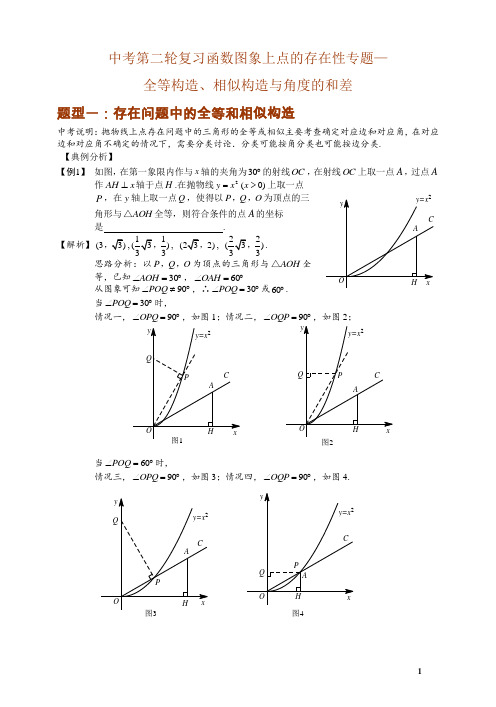
中考第二轮复习函数图象上点的存在性专题—全等构造、相似构造与角度的和差题型一：存在问题中的全等和相似构造中考说明：抛物线上点存在问题中的三角形的全等或相似主要考查确定对应边和对应角，在对应边和对应角不确定的情况下，需要分类讨论．分类可能按角分类也可能按边分类. 【典例分析】【例1】 如图，在第一象限内作与x 轴的夹角为30︒的射线OC ，在射线OC 上取一点A ，过点A作AH x ⊥轴于点H .在抛物线2y x =(0)x >上取一点P ，在y 轴上取一点Q ，使得以P Q O ，，为顶点的三角形与AOH △全等，则符合条件的点A 的坐标是 .【解析】(3,1)3，, 2), 2)3，. 思路分析：以P Q O ，，为顶点的三角形与AOH △全等，已知30AOH ∠=︒，60OAH ∠=︒ 从图象可知90POQ ∠≠︒，∴30POQ ∠=︒或60︒. 当30POQ ∠=︒时，情况一，90OPQ ∠=︒，如图1；情况二，90OQP ∠=︒，如图2；当60POQ ∠=︒时，情况三，90OPQ ∠=︒，如图3；情况四，90OQP ∠=︒，如图4.图4【例2】 如图，抛物线22y ax ax c =-+（0a ≠）交x 轴于A 、B 两点，A 点坐标为（3，0），与y 轴交于点()04C ，，以OC 、OA 为边作矩形OADC 交抛物线于点G .（1）求抛物线的解析式；（2）抛物线的对称轴l 在边OA （不包括O 、A 两点）上平行移动，分别交x 轴于点E ， 交CD 于点F ，交AC 于点M ，交抛物线于点P ，若点M 的横坐标为m ，请用含m 的代数式表示PM 的长.（3）在（2）的条件下，连结PC ，则在CD 上方的抛物线部分是否存在这样的点P ， 使得以P 、C 、F 为顶点的三角形和AEM △相似？若存在，求出此时m 的值，并直接判断PCM △的形状；若不存在，请说明理由.(2013凉山)【解析】（1）∵()04C ，，()30A ，在抛物线()220y ax ax c a =-+≠上 ∴4960c a a c =⎧⎨-+=⎩解得：434a c ⎧=-⎪⎨⎪=⎩………………………………………（2分） ∴所求抛物线的解析式为：248433y x x =-++…………………………（3分）（2）设直线AC 的解析式为()0y kx b k =+≠∵()()3004A C ，，，在直线AC 上 ∴304k b b +=⎧⎨=⎩解得：434k b ⎧=-⎪⎨⎪=⎩∴直线AC 的解析式为：443y x =-+……………………（4分）∴443M m m ⎛⎫-+ ⎪⎝⎭，，248433P m m m ⎛⎫-++ ⎪⎝⎭，………………（5分）∵点P 在M 上方∴248444333PM m m m ⎛⎫=-++--+ ⎪⎝⎭248444333m m m =-+++-2443m m =-+……………………………………（6分）（3）①若PFC AEM △△，此时PCM △是直角三角形且90PCM =∠° 则PF CF AE ME =即PF AE CF ME=…………………………………………（7分） A B Cl PMFG DO Ex y又∵AEM AOC △△ ∴AE ME AE OA OA OC ME OC -=即 ∴34PF OA CF OC ==…………………………………………………………（8分） ∵224848443333PF PE EF m m m m =-=-++-=-+ CF OE m ==∴2483334m mm -+= ∵0m ≠，∴2316m =…………………………………………………………………………（9分）②若CFP AEM △△此时PCM △是等腰三角形且PC CM = 则PF FC ME AE =即PF ME FC AE=…………………………………………………………（10分） 由①得34OA AE OC ME ==∴43OC OA = ∴43PF OC FC OA ==………………………………………………………………………（11分） 同理24833PF m m =-+，CF OE m ==∴2484333m mm -+=∵0m ≠，∴1m =综合所得：存在这样的点P 使PFC △与AEM △相似此时m 的值为2316或1，PCM △为直角三角形或等腰三角形……………………（12分）题型二：存在问题中的角度【存在问题中的角度---特殊角】中考说明：单个特殊角θ一般指30︒、45︒、60︒等，初中阶段主要考察如何利用特殊角度去构造特殊三角形，从而解决相关问题；初高中衔接知识是特殊直线tan y x m θ=⋅+与抛物线()20y ax bx c a =++≠的交点.45°30°特殊角度 构造特殊三角形典题精练【例3】⑴如图1，在平面直角坐标系xOy 中，点P 为抛物线2y x =上一动点，是否存在点P 使 得直线OP 与x 轴的正半轴的夹角为45︒，若存在，请求出点P 的坐标；不存在，说明 理由．⑵如图2，在平面直角坐标系xOy 中，点P 为抛物线2y x =上一动点，点A 的坐标为104⎛⎫ ⎪⎝⎭，，是否存在点P 使得直线PA 分别与x 轴正半轴的夹角为45︒或30︒？若存在，请求出点P 的坐标；不存在，说明理由．【解析】 ⑴方法一：如图3，过点P 作PK x ⊥轴于点K ，由已知得45POK ∠=︒，POK △为等腰直角三角形.设点P 的坐标为()2x x ，，则2PK x OK x ==，， 故PK OK =，则2x x =，∴0x =（舍），1x =，∴点P 的坐标为()11，． 方法二：∵45POx =︒∠，∴直线OP 是第一象限的角平分线， 故直线OP 的解析式为y x =，点P 即为抛物线和直线OP 的交点（点O 除外），联立方程组2y x y x ⎧=⎨=⎩，解得00x y =⎧⎨=⎩（舍），11x y =⎧⎨=⎩，故点P 的坐标为()11，． ⑵如图4，若直线PA 与x 轴正半轴的夹角为45︒，且直线PA 与y 轴交于点B . ∴AOB △为等腰直角三角形，14OA OB ==，∴点B 的坐标为104⎛⎫- ⎪⎝⎭，由待定系数法可求直线PA 的解析式为14y x =-，联立方程组214y x y x ⎧=⎪⎨=-⎪⎩解得1214x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴点P 的坐标为1124⎛⎫⎪⎝⎭，．如图5，若直线PA 与x 轴正半轴的夹角为30︒，且直线PA 与y 轴交于点C.∴30OAC∠=︒，在Rt OAC△中，OA，∴OC=∴点C的坐标为0⎛⎝⎭，由待定系数法可求直线PA的解析式为y=-，联立方程组2y xy x⎧=⎪⎨=⎪⎩得20 x=，240⎛-<⎝⎭，故方程无实数根，故点P不存在．【例4】如图，在平面直角坐标系xOy 中，点P 为抛物线2y x =上一动点，点A 的坐标为()42，，若点P 使45AOP =︒∠，请求出点P 的坐标．【解析】 方法一：构造外弦图，如图1，过点A 作MN 垂直x 轴于M ，在AN 上取点N ，使得AN OM =，过点N 作NK OM ∥，过点A 作AK AO ⊥，AK 与NK 相交于点K ． 易证AMO KNA △≌△∴4AN OM ==，2NK AM == ∴点K 的坐标为()26，直线OK 的解析式为3y x =联立方程组23y x y x⎧=⎨=⎩解得00x y =⎧⎨=⎩（舍），39x y =⎧⎨=⎩故点P 的坐标为()39，．方法二：如图2，以AO 为斜边作等腰直角三角形AOK ，再构造弦图，求K 的坐标．2．【存在问题中的角度---构造角度相等或角度和】【例5】已知抛物线22y x x c=-+与x轴交于A，B两点，与y轴交于C点，抛物线的顶点为D 点，点A的坐标为()10-，．⑴求D点的坐标；⑵如图1，连接AC，BD，并延长交于点E，求E∠的度数；⑶如图2，已知点()40P-，，点Q在x轴下方的抛物线上，直线PQ交线段AC于点M，当PMA E∠=∠时，求点Q的坐标．(2013十堰)x图1图2x【解析】（1）把x=－1，y=0代入22y x x c得1＋2＋c=0，∴c=－3∴222314y x x x∴顶点D的坐标为（1，－4）（2）如图1，连结CD、CB,过D作DF⊥y轴于F点，由2230x x得x1=－1，x2=3，∴B（3,0）．当x=0时，2233y x x．∴C（0,－3），∴OB=OC=3，∵∠BOC=90°，∴∠OCB=45°，BC=又∵DF=CF=1，∠CFD=90°，∴∠FCD=45°，CD，∴∠BCD=180°－∠OCB－∠FCD =90°．∴∠BCD =∠COA．11,=33CD OACB OC又图1∴=CD OACB OC，∴△DCB ∽△AOC ，∴∠CBD =∠OCA ． 又∠ACB =∠CBD +∠E =∠OCA +∠OCB ，∴∠E =∠OCB =45°．(3)如图2，设直线PQ 交y 轴于N 点，交BD 于H 点，作DG ⊥x 轴于G 点． ∵∠PMA =45°，∴∠EMH =45°，∴∠MHE =90°， ∴∠PHB =90°，∴∠DBG +∠OPN =90°．又∠ONP +∠OPN =90°，∴∠DBG =∠ONP ，又∠DGB =∠PON =90°，∴△DGB ∽△PON ， ∴2==44BG ON ONDG OP ,即， ∴ON =2，∴N （0，－2）．设直线PQ 的解析式为y =kx +b ， 则由40,2.k b b 解得k =－12，b =－2， ∴122y x ．设Q （m ，n ）且n <0，∴122nm ． 又Q （m ，n ）在223yx x 上，∴223nm m ， ∴212232m m m ，解得1212,2m m ， ∴1273,4n n ， ∴点Q 的坐标为（2，－3）或（－12，－74）.-1y x-4M QGNHEPA CB DO Q目标班训练1. 已知：抛物线2y ax bx c =++与x 轴交于点()20A -，、()80B ，，与y 轴交于点()04C -，．直线y x m =+与抛物线交于点D 、E （D 在E 的左侧），与抛物线的对称轴交于点F ．⑴求抛物线的解析式；⑵当2m =时，求DCF ∠的大小；⑶若在直线y x m =+下方的抛物线上存在点P ，使得45DPF ∠=°，且满足条件的点P 只有两个，则m 的值为 ．（第⑶问不要求写解答过程）备用图2备用图1（海淀期末）【解析】 ⑴ 依题意，设抛物线的解析式为()()28y a x x =+-．∵抛物线与y 轴交于点()04C -，，∴()()40208a -=+-．解得14a =．∴抛物线的解析式为()()1284y x x =+-，即213442y x x =--．⑵ 由⑴可得抛物线的对称轴为3x =．∵2m =，∴直线的解析式为2y x =+．∵直线2y x =+与抛物线交于点D 、E ，与抛物线的对称轴交于点F ，∴F 、D 两点的坐标分别为()35F ，，()20D -，．设抛物线的对称轴与x 轴的交点为M ． 可得 5.CM FM MD ===∴F 、D 、C 三点在以M 为圆心，半径为5的圆上．∴DCF ∠=1452DMF ∠=°．⑶ 54m =-．【点评】 ⑶小问：无论直线y x m =+平移到什么位置，只要与抛物线有两个交点，那么D 点关于对称轴的对称点D '一定满足45FD D '=︒∠，因此要使满足45DPF =︒∠的点P 只有两个．则F 、D 、P 三点确定的圆一定经过抛物线的顶点，即四边形FDPD '是正方形，那么只要求出顶点坐标及D '点坐标即可．训练2. 如图，已知抛物线224323m m x m x m y -+-+-=)()(的顶点A 在双曲线xy 3=上, 直线y =mx +b 经过点A , 与y 轴交于点B , 与x 轴交于点C . ⑴确定直线AB 的解析式;⑵将直线AB 绕点O 顺时针旋转90︒, 与x 轴交于点D , 与y 轴交于点E , 求sin ∠BDE 的值;⑶过点B 作x 轴的平行线与双曲线交于点G , 点M 在直线BG 上, 且到抛物线的对 称轴的距离为6. 设点N 在直线BG 上, 请你直接写出使得∠AMB +∠ANB =45︒的点N 的坐标.（海淀二模）∵点A 在双曲线xy 3=上,∴xy =3.-m 2+5m -3=3.解得 m =2, m =3(不合题意, 舍去). ∴ m =2, A (1, 3).∵直线y =mx +b 经过点A , ∴3=2×1+b . b =1.故直线AB 的解析式为 y =2x +1⑵ 由y =2x +1, 可得B (0, 1), C (21-, 0).将直线AB 绕点O 顺时针旋转90°, 得点B 的对应点为D (1, 0),点C 的对应点为E (0, 21).可得直线DE 的解析式为2121+-=x y图2E由211122y x y x =+⎧⎪⎨=-+⎪⎩ 得两直线交点为F (1355-，)可得DE ⊥BC , BD =2, BF =55, ∴ sin ∠BDE =1010=BD BF . N 1(5, 1), N 2(-3, 1).训练3. 如图，已知抛物线211(1)444by x b x =-++y = (b 是实数且b >2)与x 轴的正半轴分别交于点A 、B （点A 位于点B 的左侧），与y 轴的正半轴交于点C ．(1)点B 的坐标为 ，点C 的坐标为 （用含b 的代数式表示）；⑵请你探索在第一象限内是否存在点P ，使得四边形PCOB 的面积等于2b ，且△PBC 是以点P 为直角顶点的等腰直角三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；⑶请你进一步探索在第一象限内是否存在点Q ，使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q 的坐标；如果不存在，请说明理由．【解析】 (1)点B 的坐标为（b ，0），点C 的坐标为(0,)4b(2)假设存在这样的点P ，使得四边形PCOB 的面积等于2b ，且△PBC 是以点P 为直角顶点的等腰直角三角形． 设点P 坐标为（x ,y ），连接OP ， 则S 四边形PCOB =S △PCO +S △POB =112242b x b y b += ∴x +4y =16,过点P 作PD ⊥x 轴，PE ⊥y 轴，垂足分别为D 、E ． ∴∠PEO =∠EOD =∠ODP =90°， ∴四边形PEOD 是矩形， ∴∠EPD =90°，∵△PCB 是等腰直角三角形， ∴PC=PB ，∠CPB =90°， ∴∠EPC =∠DPB ， ∴△PEC ≌△PDB ，∴PE =PD ，即x =y ,由416x y x y =⎧⎨+=⎩,解得：165165x y ⎧=⎪⎪⎨⎪=⎪⎩由△PEC ≌△PDB 得，EC=DB ，即1616545b b -=-， 解得：128225b =>，符合题意，∴P 点坐标为（165 ,165 ）(3)由2111(1)(1)()4444b y x b x x x b =-++=--，得A （1,0），OA =1 ①如图3，以OA 、OC 为邻边构造矩形OAQC ， 那么△OQC ≌△QOA当BA QA QA OA =,即2QA BA OA =时，△BQA ∽△QOA ， 所以2()14b b =-解得8b =±Q为(1,2+②如图4，以OC 为直径的圆与直线x =1交于点Q ，那么90,OQC ∠=︒因此 △OCQ ∽△QOA 当BA QAQA OA=时，△BQA ∽△QOA ，此时90OQB ∠=︒ 所以C 、Q 、B 三点共线，因此BO QACO OA=即14b QA b =，解得QA =4,此时Q （1,4）目标123班训练1. 二次函数223y x x =--的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于C 点，在二次函数的图象上是否存在点P ，使锐角PCO ACO ∠>∠？若存在，请你求出P 点的横坐标的取值范围；若不存在，请你说明理由．【分析】 探索的点必须满足两个条件：①PCO ∠为锐角；②PCO ACO ∠>∠．借助探索问题五的思想方法寻找临界点（PCO ACO ∠=∠）．【解析】 存在点P ，使得锐角PCO ACO ∠>∠．取A 点关于y 轴的对称点D ．连结CD 并延长交抛物线于M过C 作CN x ∥轴交抛物线于N 点．显然当P 点在M 、N 之间或在A 、C 之间的抛物线上时，锐角PCO ACO ∠>∠． ∴A （1-，0），C （0，3-），D （1，0）． ∴直线CD 的解析式为：33y x =-．联立23323y x y x x =-⎧⎨=--⎩得：1103x y =⎧⎨=-⎩或22512x y =⎧⎨=⎩ ∴M 点的横坐标为5．由抛物线的对称性知：C 、N 关于对称轴对称， ∴N 点的横坐标为2．∵当P 点在M 、N 之间或在A 、C 之间的抛物线上时， 锐角PCO ACO ∠>∠． ∴10p x -<<或25p x <<．【点评】 ⑴ 由点及线的问题转化思想．⑵ 本例还可变形为：探索点P ，使PAC △的内心在y 轴左侧？内心在第三象限？训练2. 抛物线213122y x x =-+过点()10A ，，()20B x ，，交y 轴正半轴于点C ，在抛物线上（在B 点的右侧）是否存在一点P ，使得PCB CBA ACB ∠<∠-∠？若存在，求出P 点的横坐标的取值范围；若不存在，请说明理由．【分析】 探索条件是一个不等关系，这样的问题都可仿照探索五的思想方法，寻找临界点（PCB CBA ACB ∠=∠-∠）【解析】 在抛物线上（在B 点的右侧）存在一点P ，使PCB CBA ACB ∠<∠-∠．设CP 交x 轴于点D ，显然，()20B ，，()01C ，， 当PCB CBA ACB ∠=∠-∠时，PCB ACB CBA ∠+∠=∠，∴ACB ADC △∽△，∴2AC AB AD =⋅，∴2AD =，∴()30D ，，∴直线CP ：113y x =-+，由211313122y x y x x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，有7239P ⎛⎫ ⎪⎝⎭，．∴当PCB CBA ACB ∠<∠-∠时，723x <<． 【点评】 ①将问题特殊化，利用相似三角形，探讨三个角满足等量关系时点的坐标，在根据函数及图象的性质，得到解答；②第⑵问拓展；在抛物线上（在B 点的右侧）是否存在一点P ，使45PCB ∠=°？若存在，求出点P 的坐标；若不存在，请说明理由．训练3. 如图，平行四边形ABCD 的顶点()120A -，()09B ，，2104C ⎛⎫ ⎪⎝⎭，，抛物线2y ax bx c =++点A 、B ．⑴求点D 的坐标．⑵关于x 的方程221344ax bx c x ++-=个解，求抛物线的解析式．⑶在⑵的条件下，点P 为抛物线2y ax bx c =++一动点（不与A 、B 重合），过点P 作x 交线段CD 于Q ，若45AQD BQC =︒-∠∠【解析】 ⑴ 15124D ⎛⎫-- ⎪⎝⎭，．⑵ 把()120A -，，()09B ，代入2y ax bx c =++中得3124b a =+∴23213129444ax a x x ⎛⎫+++-= ⎪⎝⎭即2151204ax ax ++=∴()212150a a ∆=-=，0a =（舍），2548a =∴2b =，抛物线的解析式为252948y x x =++．⑶ 3-或 5.4-．题型一 存在问题中的全等和相似构造 巩固练习【练习1】 如图，二次函数2162y x =-+的图象与x 轴交于A 、B 两点，顶点为N ．⑴设点P 、Q 为该二次函数的图象在x 轴上方的两个动点，试猜想：是否存在这样的点P 、Q ，使AQP ABP △≌△？如果存在，请举例验证你的猜想；如果不存在，请说明理由．⑵若直线AK 交y 轴于点K ，且AOK NOA △∽△，求点K 的坐标.（泰州中考改编）【解析】⑴ 存在．设抛物线顶点为()06N ，，在RtAON △中，易得AN =，于是以A 点为圆心， AB =x 上方一定有交点()1Q N 、2Q ，如图1，连接1AQ ，再作1Q AB ∠平分线1AP 交抛物线于1P ，连接1BP 、11PQ ，此时由“边角边”易得111AQ P ABP △≌△． （或连接2AQ ，再作2Q AB ∠平分线2AP 交抛物线于2P ，连接2BP 、22P Q ，此时由“边角边”易得222AQ P ABP △≌△） ⑵∵AOK NOA △∽△∴AO OKNO OA ==2OK = 故点K 的坐标为()02，或)02-，.题型二 存在问题中的角度 巩固练习【练习2】 如图，在平面直角坐标系xOy 中，点P 为抛物线2y x =上一动点，点A 的坐标为()10，.⑴若点P 使得60POA ∠=︒，求出点P 的坐标；⑵若点P 使得直线AP 与x 轴正方向的夹角最小，请求出点P 的坐标．【解析】 ⑴ 设点P 的坐标为()2x x ，，如图1，过点P 作PH x⊥轴于点H ,2tan PH x POH OH x ∠==∴x =P 的坐标为)3.⑵ 如图2，直线PA 经过点()10，， 设PA 的解析式为y kx k =-．联立方程组2y x y kx k ⎧=⎨=-⎩，当PAx ∠最小时，方程2x kx k =-有唯一解， ()240k k ∆=--=，0k =（舍），4k =，故直线PA 的解析式为44y x =-． 点P 的坐标为()24，．。

三、因动点产生的直角三角形问题四、因动点产生的平行四边形问题7、如图，在Rt△ABC中，∠C＝向点C以每秒1个单位长度的速度运动，位长度的速度运动，过点P作PD//BC4五、因动点产生的梯形问题例9、已知直线y＝3x－3分别与x轴、B．（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线（2）点P为线段OC上的一个动点，过点N，问是否存在这样的点P，使得四边形的坐标；若不存在，请说明理由；（3）若△AOB沿AC方向平移（点六、因动点产生的面积问题例11、如图，在平面直角坐标系中放置一直角三角板，将此三角板绕原点O逆时针旋转90°，得到三角形（1）一抛物线经过点A′、B′、B，求该抛物线的解析式；（2）设点P是第一象限内抛物线上的一个动点，是否存在点面积是△A′B′O面积的4倍？若存在，请求出点学科组长审核签字：----------------------------------------------------------------------------------------------------------------------- ----------------------------------------------------------------------------------------------------------------------- ------------------------------------------------------------------------------------------------------------------------ ------------------------------------------------------------------------------------------------------------------------- -----------------------------------------------------------------------------------------------------------------------。

`中考说明：从07到13年我们发现各区模拟和中考中有很多考题通过距离来限制动点的位置．比如寻找等腰三角形的顶点等等． 一、线段定值问题：初中知识涉及点到点的距离，点到线的距离，平行线的距离，距离问题可分为以下几类：① 动点P 到定点O 的距离等于定长d ，其实就是作圆（如图1）． ② 动点P 到定直线l 的距离等于定长d ，其实就是作平行线（如图2）． ③ 动点P 到两定平行直线的距离倍差，其实是作平行线（图略）． ④ 动点到两相交直线的距离相等，其实就是作角平分线．（如图3）⑤ 动点到三角形三边的距离相等，其实就是三角形的内切圆圆心和旁切圆圆心（如图4）．4第二轮复习之函数图像上点的存在性问题中的距离、面积与角度题型一：存在问题中的距离28二、线段最值问题： 题型一：已知AB a =，AC b =，其中a b <，求BC 的最值．如图，以点A 为圆心，线段AB 为半径作圆， A ⊙交直线AC 于点1B 、2B ，当点B 与点1B 重合时，BC 取到最大值为a b +；当点B 和点2B 重合时，BC 取到最小值为b a -．点评：首尾相连线段求最值，其实就是旋转共线，不重则大，重叠则小．题型二：在直线l 上找一点P ，使得其到直线同侧两点A B 、的距离之和最小，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，与l 的交点即为P 点．题型三：直线12l l 、交于O ，P 是两直线间的一点，在直线12l l 、上分别找一点A B 、，使得PAB △的周长最短．如图所示，作P 点关于12l l 、的对称点12P P 、，连接12P P ，与12l l 、分别交于A B 、两点，即为所求．题型四：直线12l l 、交于O ，A B 、是两直线间的两点，从点A 出发，先到1l 上一点P ，再从P 点到2l 上一点Q ，再回到B 点，求作P Q 、两点，使AP PQ QB ++最小．如图所示，作A B 、两点分别关于直线12l l 、的对称点A B ′′、，连接A B ′′分别交12l l 、于P Q 、，即为所求． 点评：同侧定点问题通过轴对称转化成异侧定点，才能和直线相交．图4I 3I 2I 1IB 1B 2CBAA'BP AlOl 1l 2QPB'A'BAOB AP 2P 1P l 2l 1题型五：从A 点出发，先到直线l 上的一点P ，再在l 上移动一段固定的距离PQ ，再到点B ，求作P 点使移动的距离最短，如图所示．先将A 点向右平移到A ′点，使AA ′等于PQ 的长，作点B 关于l 的对称点B ′，连接A B ′′，与直线l 的交点即为Q 点，将Q 点向左平移线段PQ 的长，即得到P 点．题型六：A B 、是位于河两岸的两个村庄，要在这条宽度为d 的河上垂直建一座桥，使得从A 村庄经过桥到B 村庄所走的路程最短．如图所示，将点A 向垂直于河岸的方向向下平移距离d ，到A ′点，连接A B ′交河岸于Q 点，过Q 点作PQ 垂直于河岸，交河岸的另一端为P ，即为所求． 点评：若有定长，则按着定长的方向平移掉定长．题型七： 垂线段最短．AB ≥AM+BNNBMA斜边大于直角边C B A垂线段最短B'A'QPBAl30【例1】 在平面直角坐标系xOy 中，抛物线223y mx mx n =++经过(35)P ，，(02)A ，两点．⑴求此抛物线的解析式；⑵设抛物线的顶点为B ，将直线AB 沿y 轴向下平移两个单位得到直线l ，直线l 与抛物线的对称轴交于C 点，求直线l 的解析式；⑶在⑵的条件下，求到直线OB 、OC 、BC 距离相等的点的坐标． （北京中考）【例2】 已知抛物线21y ax bx =++经过点()13A ，和点()21B ，． ⑴求此抛物线解析式； ⑵点C 、D 分别是x 轴和y 轴上的动点，求四边形ABCD 周长的最小值； ⑶过点B 作x 轴的垂线，垂足为E 点．点P 从抛物线的顶点出发，先沿抛物线的对称轴到达F 点，再沿FE 到达E 点，若P 点在对称轴上的运动速度是它在直线FE 上运动速度的2倍，试确定点F 的位置，使得点P 按照上述要求到达E 点所用的时间最短．（要求：简述确定F 点位置的方法，但不要求证明）典题精练yx 331221O中考说明：经过分析统计近三年北京模拟题和外地中考题，发现二次函数综合题中涉及面积的题目所占比例极大，其原因大致有两点：一是面积可以通过底和高来限制线段，二是特殊图形面积计算也是中考的考查点．【例3】 抛物线223y x x =--+与x 轴交于点A 、B （点A 在点B 右侧），与y 轴交于点C ，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．【例4】 如图，已知抛物线212y x bx c =++（b ，c 是常数，且0c <）与x 轴分别交于点A ，B （点A 位于点B 的左侧），与y 轴的负半轴交于点C ，点A 的坐标为(10)-，．⑴ b ＝ ，点B 的横坐标为 （上述结果均用含c 的代数式表示）；⑵ 连接BC ，过点A 作直线AE BC ∥，与抛物线212y x bx c =++交于点E ．点D 是x 轴上一点，其坐标为()20，，当C ，D ，E 三点在同一直线上时，求抛物线的解析 式；⑶ 在⑵的条件下，点P 是x 轴下方的抛物线上的一动点，连接PB ，PC ，设所得△PBC 的面积为S ． ①求S 的取值范围；②若△PBC 的面积S 为整数，则这样的△PBC 共有 个．（2013苏州）典题精练题型二：存在问题中的面积ExOyCBAODCBA yx321.【存在问题中的角度---特殊角】中考说明：单个特殊角θ一般指30︒、45︒、60︒等，初中阶段主要考察如何利用特殊角度去构造特殊三角形，从而解决相关问题；初高中衔接知识是特殊直线tan y x m θ=⋅+与抛物线()20y ax bx c a =++≠的交点.【例5】 ⑴如图1，在平面直角坐标系xOy 中，点P 为抛物线2y x =上一动点，是否存在点P 使得直线OP 与x 轴的正半轴的夹角为45︒，若存在，请求出点P 的坐标；不存在，说明理由．⑵如图2，在平面直角坐标系xOy 中，点P 为抛物线2y x =上一动点，点A 的坐标为104⎛⎫⎪⎝⎭，，是否存在点P 使得直线PA 分别与x 轴正半轴的夹角为45︒或30︒？若存在，请求出点P 的坐标；不存在，说明理由．典题精练构造特殊三角形特殊角度45°30°题型三：存在问题中的角度y PO xA 图2y O P x2．【存在问题中的角度---构造角度相等或角度和】 【例6】 在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A B ，两点（点A 在点B 的左侧），与y 轴交于点C ，点B 的坐标为(30)，，将直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ，两点． ⑴求直线BC 及抛物线的解析式；⑵设抛物线的顶点为D ，点P 在抛物线的对称轴上，且APD ACB ∠=∠，求点P 的坐标；⑶连接CD ，求OCA ∠与OCD ∠两角和的度数．（北京中考）34题型一 存在问题中的距离 巩固练习 【练习1】 在平面直角坐标系xOy 中，抛物线2y x bx c =++经过()20A ，、()40B ，两点，直线122y x =+交y 轴于点C ，且过点(8)D m ，． ⑴求抛物线的解析式；⑵在x 轴上找一点P ，使CP DP +的值最小，求出点P 的坐标；⑶将抛物线2y x bx c =++左右平移，记平移后点A 的对应点为A '，点B 的对应点为B '，当四边形A B DC ''的周长最小时，求抛物线的解析式及此时四边形A B DC ''周长的最小值．（顺义二模）复习巩固【练习2】 如图，正比例函数和反比例函数的图象都经过点()33A ，，把直线OA 向下平移后， 与反比例函数的图象交于点()6B m ，，与x 轴、 y 轴分别交于C 、D 两点.⑴求m 的值；⑵求过A 、B 、D 三点的抛物线的解析式；⑶若点E 是抛物线上的一个动点，是否存在点E ，使凸四边形OECD 的面积1S 是四边形OACD 面积S 的23?若存在，求点E的坐标；若不存在，请说明理由．36【练习3】 如图，点P 是直线l ：22y x =--上的点，过点P 的另一条直线m 交抛物线2y x =于A 、B 两点．⑴ 若直线m 的解析式为1322y x =-+，求A ，B 两点的坐标；⑵ ① 若点P 的坐标为()2t -，．当PA AB =时，请直接写出点A 的坐标； ② 试证明：对于直线l 上任意给定的一点P ，在抛物线上能找到点A ，使得PA AB = 成立． ⑶ 设直线l 交y 轴于点C ，若AOB △的外心在边AB 上，且BPC OCP ∠=∠，求点P 的 坐标．（2013武汉）ml yxOB APO xylCPAB O xyl m第十八种品格：坚持铁杵成针相传唐代大诗人李白在小的时候很贪玩，不爱读书，也不求上进。

专题4.1函数（知识梳理与考点分类讲解）【知识点1】函数的定义1.函数的定义一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量.说明:(1)在函数中定义的两个变量x,y是有主次之分的,变量x的变化是主动的,称之为自变量,而变量y是随x的变化而变化的,是被动的,称之为因变量(即自变量的函数);(2)函数不是数,函数的实质是两个变量的对应关系.2.判断一个关系是否是函数关系的方法一看是否在一个变化过程中;二看是否存在两个变量;三看对于变量每取一个确定的值,另一个变量是否都有唯一确定的值与其对应,以上三者(简称“三要素”)缺一不可.特别提醒：函数的定义中包括了对应值的存在性唯一性两重薏思，即对自变量的每一个确定的值函数有且只有一个值与之对应对自变量x的不同值y的值可以相同，如函数2y x ,当x=1和x=-1时,y的对应值者是L 【知识点2】函数的三种表示方法1.函数的三种表示方法表示方法定义优点缺点列表示通过列出自变量的值与对应函数值的表格表示函数关系的方法叫做列表法一目了然,对表格中已有自变量的每一个值,可直接查出与它对应的函数值列出的对应值是有限的,而且在表格中也不容易看出自变量与函数的变化规律关系式法用数学式子表示函数关系的方法叫做关系式法.其中的等式叫做函数关系式能准确地反映整个变化过程中自变量与数值的对应关系从函数关系式很难直观看出函数的变化规律,而且有些函数不能用关系式法表示出来图象法用图象表示两个变量间的函数关系的方法叫做图象法直观、形象地反映出函数关系变化的趋势和某些性质从自变量的值常常难以找到对应函数的准确值2.列函数关系式根据实际问题列函数关系式的方法类似于列方程解应用题，只要找出自变量与函数值之间存在的等量关系，列出等式即可.但要整理成用含自变量的代数式表示函数值的形式.【考点一】利用函数的概念判断两变量的函数关系【例1】（2023·上海·八年级假期作业）下列各式中，y 是否是x 的函数？为什么？（1）23y x =；（2）23y x =．【答案】（1）是，理由见分析；（2）不是，理由见分析【分析】根据函数的概念进行求解即可：对于两个变量，对于其中一个变量x 的任意取值（取值范围内），另一个变量y 都有唯一的值与之对应，那么y 就是x 的函数．（1）解：∵在23y x =中，对于任意的x 的值，y 都有唯一的值与之对应，∴y 是x 的函数；（2）解：∵在23y x =中，对于任意一个正数x 的值，y 都有两个值与之对应，∴y 不是x 的函数；【点拨】本题主要考查了函数的定义，熟知函数的定义是解题的关键．【举一反三】【变式1】（2023秋·安徽合肥·八年级合肥38中校考阶段练习）下列各曲线中，能表示y 是x 的函数的是（）A ．B ．C ．D ．【答案】D【分析】根据函数的概念即可解答．解：由函数的定义：在一个变化过程中有两个变量x 与y ,对于x 的每一个确定的值，y 都有唯一的值与其对应，那么就说y 是x 的函数．则只有D 选项符合题意故选：D ．【点拨】题主要考查了函数的概念，在一个变化过程中有两个变量x 与y ,对于x 的每一个确定的值，y 都有唯一本的值与其对应，那么就说y 是x 的函数．【变式2】（2023·山东德州·二模）下列关于两个变量关系的四种表述中，正确的是．（填序号即可）①圆的周长C 是半径r 的函数；②表达式y =y 是x 的函数；③如表中，n 是m 的函数；m 3-2-1-123n2-3-6-632④如图中，曲线表示y 是x 的函数．【答案】①②③【分析】根据函数的定义与函数的表示方法逐一分析即可得到答案．解：①圆的周长C 是半径r 的函数；表述正确，故①符合题意；②表达式y =y 是x 的函数；表述正确，故②符合题意；③由表格信息可得：对应m 的每一个值，n 都有唯一的值与之对应，故③符合题意；在④中的曲线，当0x >时的每一个值，y 都有两个值与之对应，故④不符合题意；故答案为：①②③【点拨】本题考查的是函数的定义，函数的表示方法，理解函数定义与表示方法是解本题的关键．【考点二】函数的解析式★★自变量★★因变量【例2】（2022秋·八年级课时练习）在一次实验中，老师把一根弹簧秤的上端固定，在其下端悬挂物体，测得弹簧秤的长度()cm y 随所挂物体的质量x ()kg 变化关系的图象如下：（1）根据图象信息补全表格：x /kg 012345y /cm810121416（2）写出所挂物体质量在0至5kg 时弹簧秤长度y ()cm 与所挂物体质量()kg x 的关系式；（3）结合图象，写出弹簧秤长度是怎样随悬挂物体质量的变化而变化的．【答案】（1）18；（2）=2+8y x ；（3）当0≤x ≤5时，所挂重物每增加1千克，弹簧增长2cm ；当挂重物不小于5千克时，弹簧的长度均为18cm ．【分析】（1）根据表格可知，发现所挂重物每增加1千克，弹簧增长2cm ，据此解答即可；（2）根据弹簧的长度等于弹簧原来的长度+弹簧伸长的长度列出关系式；（3）结合图象解答即可．解：（1）由题意可知，当x =5时，y =16+2=18，故答案为：18；（2）根据表格可知：所挂重物每增加1千克，弹簧增长2cm ，根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x 千克时，弹簧长度y =2x +8（0≤x ≤5）；（3）由图象可知，当0≤x ≤5时，所挂重物每增加1千克，弹簧增长2cm ；当挂重物不小于5千克时，弹簧的长度均为18cm ．【点拨】本题主要考查得是列函数关系式，解答本题需要同学们明确弹簧的长度=弹簧原来的长度+弹簧伸长的长度，根据表格发现所挂重物每增加1千克，弹簧增长2cm 是解题的关键．【举一反三】【变式1】（2021春·海南海口·八年级北京大学附属中学海口学校校考期中）在函数y 变量x 的取值范围是（）A ．x ≥1B ．x ≠2C ．x ≥2D ．x ≥1且x ≠2【答案】D【分析】根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，就可以求解．解：根据二次根式的意义可知：x -1≥0，即x ≥1，根据分式的意义可知：x -2≠0，即x ≠2，∴x ≥1且x ≠2．故选：D ．【点拨】本题考查了函数自变量的取值范围的确定和分式的意义．函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．【变式2】（2022春·河北邯郸·八年级校考阶段练习）如图，长为32米，宽为20米的长方形地面上，修筑宽度均为x 米的两条互相垂直的小路（图中阴影部分），其余部分作耕地，如果将两条小路铺上地砖，选用地砖的价格是60元/米2．（1）写出买地砖需要的钱数y （元）与x （米）的函数关系式为（不要求写自变量的取值范围）；（2）当3x =时，地砖的费用为元．【答案】2312060y x x =-8820【分析】（1）先求出小路的面积，然后根据买地砖需要的钱数=小路的面积⨯每平方米地砖的价格，进行计算即可解答；（2）把3x =代入（1）中所求的关系式进行计算即可解答．解：（1）由题意得：两条小路的面积为：223220(52)x x x x x +-=-米2，2260(52)312060y x x x x ∴=⨯-=-，故答案为：2312060y x x =-；（2）当3x =时，2312060312036098820x x -=⨯-⨯=（元)，答：当3x =时，地砖的费用为8820元．【点拨】本题考查了函数关系式，根据题目的已知条件结合图形求出小路的面积是解题的关键．【考点三】利用函数的三种表达方式解决问题【例3】（2023春·山东烟台·六年级统考期末）在一次实验中，马达同学把一根弹簧的上端固定，在其下端悬挂物体，测得的弹簧长度(cm)y 随所挂物体的质量(kg)x 变化关系的图象如下：（1）上表反映的变化过程中的两个变量，哪个是自变量？哪个是因变量？（2）根据以上图象补全表格：所挂物体质量/kg x 012345弹簧长度/cmy 8101214（3）由图象可知，弹簧能承受的所挂物体的最大质量是多少千克？（4）在弹簧承受范围内，请直接用含有x 的代数式表示y ．【答案】（1）图中反映的是弹簧的长度随所挂物体质量之间的变化关系，其中所挂物体的质量是自变量，弹簧的长度是因变量；（2）16，18；（3）5千克；（4）()2805y x x =+≤≤【分析】（1）根据变量常量的定义结合题意进行判断即可；（2）根据图象填写表格即可；（3）根据图象得出结论；（4）根据图象可知所挂物体质量每增加1千克，弹簧伸长2厘米，据此解答即可．解：（1）图中反映的是弹簧的长度随所挂物体质量之间的变化关系，其中所挂物体的质量是自变量，弹簧的长度是因变量；（2）由图象得：所挂物体质量/kg x 012345弹簧长度/cm y 81012141618故答案为：16，18；（3）由图象可知，弹簧能承受的所挂物体的最大质量是5千克．（4）∵所挂物体质量每增加1千克，弹簧伸长2厘米，∴()2805y x x =+≤≤．【点拨】本题考查函数的表示方法，理解表格中弹簧的长度随所挂物体质量之间的变化关系是正确判断的关键．【举一反三】【变式1】（2023春·四川达州·七年级统考期末）李强一家自驾车到离家500km 的九寨沟旅游，出发前将油箱加满油．下表记录了轿车行驶的路程(km)x 与油箱剩余油量(L)y 之间的部分数据：轿车行驶的路程/km x 0100200300400…油箱剩余油量/L y 5042342618…下列说法不正确的是（）A ．该车的油箱容量为50LB ．该车每行驶100km 耗油8LC ．油箱剩余油量(L)y 与行驶的路程(km)x 之间的关系式为508y x =-D ．当李强一家到达九寨沟时，油箱中剩余10L 油【答案】C【分析】根据表格中信息逐一判断即可．解：A 、由表格知：行驶路程为0km 时，油箱余油量为50L ，故A 正确，不符合题意；B 、0100km -时，耗油量为-=50428L ；100——200km 时，耗油量为37298L -=；故B 正确，不符合题意；C 、有表格知：该车每行驶50km 耗油4L ，则45050y x =-，故C 错误，符合题意；D 、当500x =时，()45050010L 50y =-⨯=，故D 正确，不符合题意．故选：C ．【点拨】本题主要考查了函数的表示方法，明确题意、正确从表格中获取信息是解题的关键．【变式2】（2020秋·八年级单元测试）等腰三角形ABC 周长为24，底边BC 长为y ，腰AB 长为x ，则y 关于x 的函数解析式及定义域是.【答案】()242612y x x =-<<【分析】根据三角形的周长为24可得出2x+y=24，变形后即可得出y=-2x+24；根据三角形的边长大于0以及两腰之和大于底边，即可得出关于x 的一元一次不等式组，解之即可得出自变量x 的取值范围．解：根据题意得：2x+y=24，∴y=-2x+24，∵x 、x 、y 为三角形的边，∴22242240x x x -+-+⎧⎨⎩＞＞，∴6＜x ＜12．故答案为：()242612y x x =-<<．【点拨】本题考查了一次函数的应用、等腰三角形的性质、三角形三边关系以及三角形的周长，解题的关键是：（1）根据三角形的周长为20找出y 关于x 的函数解析式；（2）由三角形的边长为正值结合两腰之和大于底边，列出关于x 的一元一次不等式组．【考点四】实际问题中列函数的表达式【例4】（2023秋·全国·八年级专题练习）某超市最近销售蓝莓，根据以往的销售经验，每天的售价与销售量之间有如下关系：每千克售价（元）6059585756……30每天销售量（千克）5055606570……200（1）表格中的自变量是__________，因变量是__________．（2）设当售价从每千克60元下降了x 元时，每天销售量为y 千克，直接写出y 与x 之间的关系式；（3）如果周六的销售量是170千克，那这天的售价是每千克多少元？（4）如果蓝莓的成本价是30元/千克，某天的售价定为40元/千克，当天的销售利润是多少？【答案】（1）每千克售价，每天销量；（2）550y x =+；（3）36元；（4）1500元【分析】（1）根据表格内容可求解此题；（2）由題意根据每千克售价每下降1元每天销售量就增加5千克进行求解；（3）将170y =代入（2）题结果并进行计算；（4）根据当天的销售利润等于每千克的利润乘以销售的千克数进行代入计算．（1）解：由题意得，自变量是每千克售价，因变量是每天销量，故答案为：每千克售价，每天销量；（2）解：由题意得售价每下降1元销售量就增大5千克，∴当售价从每千克60元下降了x 元时，每天销售量为550y x =+即y 与x 之间的关系式为550y x =+；（3）解：当170y =时，170550x =+，解得：24x =，∴602436-=，即这天的售价是每千克36元；（4）解：由（2）题结果可得，当604020x =-=时，52050150y =⨯+=，∴()40301501500-⨯=（元）答：这天的销售利润是1500元．【点拨】此题考查了运用函数解决实际问题的能力，关键是能准确理解题目间数量关系，并运用函数知识进行求解．【举一反三】【变式1】（2023春·河北邯郸·八年级统考期末）已知两个变量x 和y ，它们之间的三组对应值如下表所示：x 2-02y311-那么y 关于x 的函数解析式可能是（）A ．1y x =-+B ．21y x x =++C ．y =13x +D ．2y x=-【答案】A【分析】根据函数的定义以及函数图象上点的坐标特征逐项进行判断即可．解：A ．表格中的三组x y 、的对应值均满足1y x =-+，因此选项A 符合题意；B ．表格中01x y ==，满足21y x x =++，但23x y =-=，与21x y ==-，不满足21y x x =++，因此选项B 不符合题意；C ．表格中的三组x y 、的对应值均不满足13y x =+，因此选项C 不符合题意；D ．表格中的三组x y 、的对应值均不满足2y x =-，因此选项D 不符合题意；故选：A ．【点拨】本题考查函数关系式，理解函数的定义以及函数图象上点的坐标特征是正确解答的前提．【变式2】（2023秋·全国·八年级专题练习）甲同学的饭卡原有208元，在学校消费为周一到周五，平均每天消费35元，他的卡内余额y （元）与在校天数()05x x ≤≤之间的关系式为．【答案】20835y x=-【分析】用208减去x 天内的消费，即可确定函数关系式．解：依题意，他的卡内余额y （元）与在校天数()05x x ≤≤之间的关系式为20835y x =-，故答案为：20835y x =-．【点拨】本题考查了函数关系式，理解题意列出关系式是解题的关键．【考点五】动点问题中列函数的表达式【例5】（2023春·湖南长沙·八年级统考期末）已知点()8,0A 及在第一象限的动点(),P x y ，且10x y +=．设OPA 的面积为S ．（1）求S 关于x 的函数解析式；（2）求x 的取值范围，并根据x 的取值范围求出S 的取值范围；（3）当12S =时，求P 点坐标．【答案】（1）=-+S 4x 40；（2）010x <<，040S <<；（3）(7,3)【分析】（1）根据OPA ∆的面积S 等于1·2y OP P 可得出S 关于x 的函数解析式；（2）由点P 在第一象限，可得点P 的横纵坐标均大于0，则可得关于x 的不等式，解得x 的取值范围即可．（3）先根据（1）中S 关于x 的函数解析式及12S =，得出点P 的横坐标，再将其代入10x y +=，则可解得点P 的纵坐标．（1）解：由10x y +=得10y x =-，P 点在第一象限，点A 坐标(8,0)，∴11·8(10)44022S OA Py x x ==⨯⨯-=-+，S ∴关于x 的函数解析式为=-+S 4x 40．（2）解：P 在第一象限，∴1000x x ->⎧⎨>⎩，x ∴的取值范围为010x <<．则S 的取值范围为040S <<．（3）解：440S x =-+ ，∴当12S =时，44012x -+=，7x ∴=，710y += ，3y ∴=，P ∴点的坐标为(7,3)．【点拨】本题主要考查了求函数关系式，求自变量的取值范围，解题的关键是运用数形结合和三角形的面积公式进行计算．【举一反三】【变式1】（2023春·八年级课时练习）如图所示，在ABC 中，已知16BC =，高10AD =，动点Q 由C 点沿CB 向B 点移动（不与点B 重合）．设CQ 的长为x ，ACQ 的面积为S ，则S 与x 之间的函数关系式为（）A ．805S x =-（016x <<）B ．5S x =（016x <<）C ．10S x =（016x <<）D ．580S x =+（016x <<）【答案】B 【分析】根据三角形的面积公式即可得到S 与x 之间的函数关系式．解：∵12ACQ S CQ AD =⋅ ∴11052S x x =⨯=∴S 与x 之间的函数关系式为5S x =（016x <<）．故选：B【点拨】本题考查列函数解析式，理解题意，列出函数解析式，写出自变量的取值范围是解题的关键．【变式2】（2022秋·辽宁沈阳·八年级沈阳市实验学校校考期中）如图，在正方形ABCD 中，4AB =，动点M 从点A 出发，以每秒1个单位长度的速度沿线段AB 运动，同时动点N 从点A 出发，以每秒2个单位长度的速度沿线段AD 运动，当点N 运动到点D 时，点M ，N 同时停止运动，设AMN 的面积为y ，运动时间为x （s ），请写出y 与x 之间函数关系式．【答案】()202y x x =<≤【分析】根据点N 的运动情况，写出y 和x 之间的函数关系式即可.解：当点N 在AD 运动时，∵4AB =，∴02x <≤，∵动点M 以每秒1个单位长度的速度沿线段AB 运动，动点N 以每秒2个单位长度的速度沿线段AD 运动，∴AM x =，2AN x =，∴2122y x x x =⋅=，故答案为：()202y x x =<≤.【点拨】本题是运动型综合题，考查了函数表达式、正方形的性质、三角形的面积等知识点.解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程.【考点六】分段函数的表达式【例6】（2022秋·黑龙江大庆·七年级校考开学考试）某市自来水公司为鼓励单位节约用水，额定某单位每月计划内用水3000吨．计划内用水每吨收费1.5元，超额部分按每吨2.4元收费．（1）写出这个单位每月消费y （元）与用水量x （吨）之间的函数关系式；（2）若该单位1、2月份分别用水3200吨和2800吨，水费各为多少？【答案】（1） 1.5(03000)2.42700(3000)x x y x x <≤⎧=⎨->⎩（2）该单位1、2月份分别用水3200吨和2800吨，水费分别为4980元和4200元【分析】（1）根据题意，分03000x <≤时，3000x >时，分别列出函数关系式，即可求解；（2）将3200,2800x =分别代入（1）的关系式，即可求解．解：（1）当03000x <≤时， 1.5y x =；当3000x >时，()3000 1.53000 2.4 2.42700y x x =⨯+-⨯=-，∴y 与x 之间的函数关系式为 1.5(03000)2.42700(3000)x x y x x <≤⎧=⎨->⎩；（2）∵32003000>，∴ 2.4320027004980y =⨯-=（元），∵28003000<∴ 1.528004200y =⨯=（元），答：该单位1、2月份分别用水3200吨和2800吨，水费分别为4980元和4200元．【点拨】本题考查了列函数关系式，求函数值，根据题意分别列出函数关系式解题的关键．【举一反三】【变式1】（2022秋·福建漳州·八年级校考期中）某商店11月11日举行促销优惠活动，当天到店购买商品，有以下两种优惠方案，方案一：用168元购买会员卡后，则购买商店内任何商品，一律按商品价格的8折优惠；方案二：若不购买会员卡，则购买商店内任何商品，一律按商品价格的9折优惠．已知小敏不是该商店的会员，设她所购买商品总价格为x 元，实际支付费用为y 元．（1）若小敏不购买会员卡，则y 与x 之间的函数关系式是________；若小敏购买会员卡，则y 与x 之间的函数关系式是________；（2）小敏准备购买的商品总价格为1080元，请问她选用哪种方案较为合算？【答案】（1）0.9y x =；0.8168y x =+；（2）选用方案一较为合算【分析】（1）根据所购买商品的价格和折扣直接计算出实际应付的钱；（2）分别求出两种不同方案的实际支付费用，再比较，即可．（1）解：小敏不购买会员卡，y 与x 之间的函数关系式是0.9y x =；小敏购买会员卡，y 与x 之间的函数关系式是0.8168y x =+；故答案为：0.9y x =；0.8168y x =+（2）解：方案一：实际支付费用为0.91080972y =⨯=元；方案二：实际支付费用为0.810801681032y =⨯+=元，∵1032972>，∴小敏选用方案一较为合算．【点拨】本题考查的是列函数关系式，明确题意，准确列出函数关系式是解题的关键．【变式2】（2023春·广东茂名·七年级校考阶段练习）小明用的练习本可以到甲超市购买，也可以到乙超市购买．已知两超市的标价都是每本1元，但甲超市的优惠条件是购买10本或少于10本按标价卖，10本以上，从第11本开始按标价的70%卖．乙超市的优惠条件是从第1本开始就按标价的85%卖．（1）当小明要买28本时，到哪家超市购买较省钱？（2）写出甲超市中，收款y 甲（元）与购买本数x （本）的关系式．（3）小明现有24元钱，最多可买多少本练习本？【答案】（1）甲家超市买收费省钱；（2）()100.73(10)x x y x x ⎧≤=⎨+>⎩甲；（3）拿24元钱最多可以买30本练习本（在甲超市购买）【分析】（1）根据甲超市所需要的费用=前10本的总费用+后18本的总费用70%⨯得出甲所需要的费用，根据乙超市所需要的费用=28本的总费用85%⨯得出乙所需要的费用，然后进行比较大小得出答案；（2）甲超市所需要的费用=前10本的总费用+超出10本的总费用70%⨯得出函数解析式；（3）首先求出乙的函数解析式，然后分别求出甲和乙超市分别能买到几本练习本，从而得出答案．（1）解：买28本时，在甲超市购买需用10118170%22.6⨯+⨯⨯=（元），在乙超市购买需用28185%23.8⨯⨯=（元），22.623.8<，所以买28本到甲家超市买收费省钱；（2）解：()10y x x =≤甲101(10)170%0.73(10)y x x x =⨯+-⨯⨯=+>甲；答：()100.73(10)x x y x x ⎧≤=⎨+>⎩甲；（3）解：由题知乙超市收款y 乙（元）与购买本数x （本）间的关系式为．17185%20乙=⨯⨯=y x x 所以当24y =甲时，240.73x =+甲，解得：30x =甲；当24y =乙时，172420x =乙，28x ≈乙．所以拿24元钱最多可以买30本练习本（在甲超市购买）．【点拨】此题考查了一次函数关系式及一元一次方程等知识；求出总价y 甲与购买本数()10x x >的关系式是解题的关键．。

函数图象上的点与角度 中考说明：特殊角一般指45°、30°、60° 等； 知识点：主要考查特殊直线y ＝tan a · x ＋b 与抛物线的交点【例1】如图，在平面直角坐标系xOy 中，点P 为抛物线y ＝x 2上一动点，点A 的坐标为()，104，是否存在点P ，使∠P Ax 分别为45°或30°？若存在，请求出点P 的坐标；不存在，说明理由。

【例2】二次函数y ＝x 2－2x －3的图象与x 轴交于A 、B 两点(点A 在点B 的左侧)，与y 轴交于C 点，在二次函数的图象上是否存在点P ，使得∠P AC 为锐角？若存在，请你求出P 点的横坐标的取值范围；若不存在，请你说明理由。

函数图象上点的存在性问题中的全等、相似与角度(上)温馨提示：复习是一个很重要学习环节，希望同学们认真的去复习，把学过的知识复习一遍，从而达到温故而知新的效果。

争取在期末考试的时候取得好成绩。

你所获得每一分，都是你对知识认知的变现，你所失去的每一分，都是因为对知识的认知有缺陷。

【例3】二次函数图象经过点A (-3，0)，B (-1，8)，C (0，6)，直线y x =+223与y 轴交于点D ，点P为二次函数图象上一动点，若∠P AD ＝45°，求点P 的坐标。

【例4】(2009—2010东城二模)如图，二次函数过A (0，m )、B (-3，0)、C (12，0)，过A 点作x 轴的平行线交抛物线于一点D ，线段OC 上有一动点P ，连结DP ，作PE ⊥DP ，交y 轴于点E 。

⑴求AD 的长；⑵若在线段OC 上存在不同的两点P 1、P 2，使相应的点E 1、E 2都与点A 重合，试求m 的取值范围。

⑶设抛物线的顶点为点Q，当60°≤∠BQC≤90°时，求m的变化范围。

为你提供语文数学英语期中期末复习试卷方案说课稿等精品文档，给教学工作带来方便，提高工作效率，是这个文档价值所在，是word文档可以下载编辑,请你放心下载实用，花一点q节约时间是人生的一个聪明的选择。