机械制图轴测图
- 格式:doc
- 大小:194.26 KB
- 文档页数:15


第七章轴测图§7-1 轴测图的基本知识由于轴测图的立体感比较强,又被人们称为立体图。
轴测图的阅读无须专业知识,一般人即可看懂,而绘制也较容易,因此,在各行业中的应用都比较多,尤其在机械行业中的结构设计、工作原理图、管路图、使用说明书等,以及建筑行业的外观效果图使用更多。
一.轴测投影的形成将物体及其参考直角坐标系一同,沿不平行于任一坐标面的方向,用平行投影法投射在单一的投影面(轴测投影面)上,得到具有立体感的图形的方法,称为轴测投影,而所得图形称为轴测投影图,简称轴测图。
轴测轴: 轴测投影轴OX、OY、OZ二.轴间角和轴向伸缩系数1.轴间角:两轴测轴之间的夹角∠XOY、∠XOZ、∠YOZ。
用来控制轴测投影的形状变化。
2.轴向伸缩系数:物体上平行于直角坐标轴的直线段投影到轴测投影面上的长度,与其实际长度之比,称为轴向伸缩系数,用p、q、r分别表示OX、OY、OZ三轴的轴向伸缩系数。
用数学方法推算出来的轴向伸缩系数为非整数,给我们作图带来诸多不便,实际在绘制轴测图时,都采用简化的轴向伸缩系数。
三.轴测图的基本性质(与平行投影相同)1.平行性:若空间两直线相互平行,则其轴测投影也相互平行。
2.度量性:凡与坐标轴平行的直线段,其轴测投影必与轴测轴平行,且伸缩系数与相应轴测轴的伸缩系数相同,即可以直接度量。
(轴测图的由来)3.等比性:直线段上两线段长度之比,等于其轴测投影的长度之比。
四.轴测图的分类按投影方向对投影面的相对位置不同,将轴测图分为两大类:◆正轴测图:轴测投影方向垂直于轴测投影面。
◆斜轴测图:轴测投影方向倾斜于轴测投影面。
由于物体的参考直角坐标轴对轴测投影面的倾角不同,轴向伸缩系数也随之不同,故上面两大类又可分为以下三类:⏹正等测或斜等测,p=q=r⏹正二等测或斜二等测,p=q≠r,或p=r≠q,或q=r≠p⏹正三测或斜三测,p≠q≠r国家标准(GB4458.3-84)推荐了两种作图比较简单的轴测图:●正等轴测图●斜二等轴测图§7-2 正等轴测图一.等轴测图的轴间角和轴向伸缩系数1.轴间角:∠XOY=∠XOZ=∠YOZ=120°2.轴向伸缩系数计算出的轴向伸缩系数:p1=q1=r1=0.82简化后的轴向伸缩系数:p=q=r=1二.画正等轴测图的注意事项1.立体上平行于三个坐标轴的棱线,在轴测图上分别平行于相应的轴测轴,可以直接度量。

机械制图–轴测图概述引言机械制图是机械工程中非常重要的一门学科,它是通过图形符号来表示和传达机械零件的结构和装配关系。
在机械制图中,轴测图是一种常用的图形方案。
本文将对轴测图进行概述,包括定义、种类以及绘制方法。
轴测图的定义轴测图是一种立体空间内物体的透视图,是指根据物体的外形和空间位置关系,通过透视投影的方式将物体的形状和结构用平面图形展示出来的技术。
轴测图能够直观地表现出物体的三维外观和结构,是机械工程师设计和交流的重要工具之一。
轴测图的种类常见的轴测图有三种:等轴测图、斜轴测图和正交轴测图。
它们分别以不同的投影方式和角度来展示物体的外观和结构。
1.等轴测图:等轴测图是指视点与物体平行的一种投影方式。
在等轴测图中,物体的三个主轴在图上呈等角度分布,如30度。
2.斜轴测图:斜轴测图是指视点与物体平行但与物体的主轴不平行的一种投影方式。
在斜轴测图中,物体的一条主轴与投影面平行,而其他两条主轴倾斜。
3.正交轴测图:正交轴测图是指视点与物体的主轴相互垂直的一种投影方式。
在正交轴测图中,物体的三个主轴在图上呈90度角分布,更加直观。
轴测图的绘制方法轴测图的绘制方法主要包括透视投影和轴测投影两种方式。
1.透视投影:透视投影是指根据物体的透视关系,通过远小近大的原理将物体投影到一个透视平面上的投影方式。
在透视投影中,物体的远离观察者的部分呈现较小的尺寸,而靠近观察者的部分呈现较大的尺寸。
透视投影是一种非常直观的投影方式,能够使人们感受到真实的立体感。
2.轴测投影:轴测投影是指将物体的三维形状通过在透视平面上投影出来的平行直线来表示的投影方式。
在轴测投影中,物体的形状和结构以平行线段和平行线面来表示,不考虑透视关系。
轴测投影相对于透视投影来说更加简化,适用于工程领域中的制图需求。
在绘制轴测图时,需要掌握一些基本的绘图技巧和方法,比如确定透视点、选择适当的透视角度、绘制主轴线、使用投影线和投影面来表示物体的形状和结构等。

机械制图之轴测图1. 介绍机械制图是机械工程领域中最基础且必备的技能之一。
在机械制图中,轴测图是一种常用的表达工程设计的方法。
轴测图通过透视投影,将三维物体投影到一个平面上,使得观察者可以清楚地看到物体的各个面,从而更好地理解工程设计。
2. 轴测图的种类2.1 正交轴测图正交轴测图是最常用的一种轴测图表达方法。
它利用三个互相垂直的投影面,分别投影物体的前、上、侧面,从而形成一个立体的物体形象。
在正交轴测图中,一般使用等角投影的方法,即三个投影面上的比例尺相等。
正交轴测图可以进一步分为正加图和正减图,正加图是从右上角向左下角看,而正减图则是从左上角向右下角看。
两者的区别在于投影的角度不同,从而表达物体的不同细节。
2.2 等角轴测图等角轴测图是一种投影轴测图,它不同于正交轴测图的是等比例尺,而是保持物体的比例尺不变。
在等角轴测图中,物体的三个主要轴线呈120度夹角放置,使得观察者可以清楚地看到物体的各个面。
等角轴测图一般分为三种:等角斜二测图、等角正二测图和等角斜三测图。
等角斜二测图是最常用的一种,它将物体的三个主要轴线分别放在正前方、正左方和正上方,形成一个等角的投影。
而等角正二测图和等角斜三测图分别将物体的底面和背面呈等角投影。
3. 轴测图的制图步骤制作轴测图的步骤如下: 1. 确定物体的基本形状和尺寸。
2. 根据物体的基本形状,在纸上画出物体的三个主要轴线。
- 在正交轴测图中,这三条轴线应该垂直于彼此,并按照一定的比例排列。
- 在等角轴测图中,这三条轴线应该呈120度夹角。
3. 将物体的各个面投影到对应的投影面上。
- 在正交轴测图中,需要按照等角投影的原则,将物体的各个面投影到对应的投影面上。
- 在等角轴测图中,需要按照等比例尺的原则,将物体的各个面投影到对应的投影面上。
4. 根据投影结果,在纸上绘制出物体的各个面。
5. 在绘制出的各个面上,清晰地标注出物体的尺寸和其他必要的注释信息。

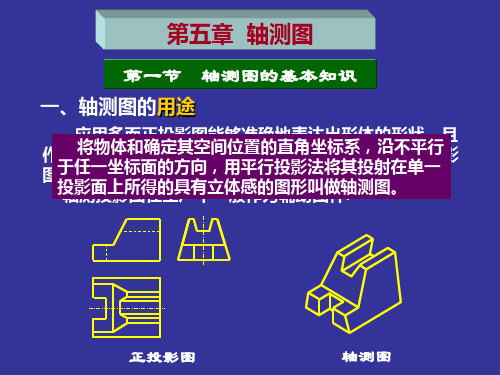
第5章轴测图工程上常用的图样是按照正投影法绘制的多面投影图,它能够完整而准确地表达出形体各个方向的形状和大小,而且作图方便。
但在图5-1a所示的三面正投影图中,每个投影图只能反映形体长、宽、高三个向度中的两个,立体感不强,故缺乏投影知识的人不易看懂,因为看图时需运用正投影原理,对照几个投影,才能想象出形体的形状结构。
当形体复杂时,其正投影就更难看懂。
为了帮助看图,工程上常采用轴测投影图(简称轴测图),如图5-1b所示,来表达空间形体。
b)a)多面正投影图与轴测投影图图5-1轴测图是一种富有立体感的投影图,因此也被称为立体图。
它能在一个投影面上同时反映出空间形体三个方向上的形状结构,可以直观形象地表达客观存在或构想的三维物体,接近于人们的视觉习惯,一般人都能看懂。
但由于它属于单面投影图,有面,而且其度量性差,作图较为复杂,因而它在应用上有一时对形体的表达不够全定的局限性,常作为工程设计和工业生产中的辅助图样,当然,由于其自身的特点,在某些行业中应用轴测图的机会逐渐增多。
5.1轴测投影的基本知识5.1.1轴测投影图的形成轴测投影属于平行投影的一种,它是用平行投影法沿某一特定方向(一般沿不平行于任一坐标面的方向),将空间形体连同其上的参考直角坐标系一起投射在选定的一个投影面上而形成的投影,如图5-2所示。
这个选定的投影面(P)称为轴测投影面,S表示投射方向,用这种方法在轴测投影面上得到的图称为轴测投影图,简称轴测图。
.轴测投影图物体图5-2 轴测投影图的形成5.1.2轴测投影的基本概念1.轴测轴如图5-2所示,表示空间物体长、宽、高三个方向的直角坐标轴OX、OY、OZ,在轴测投影面上的投影依然记为OX、OY、OZ,称为轴测轴。
2.轴间角???YOX称为轴间角。
三所示,相邻两轴测轴之间的夹角ZOYXOZ、、如图5-2个轴间角之和为360°。
3.轴向伸缩系数由平行投影法的特性我们知道,一条直线与投影面倾斜,该直线的投影必然缩短。
在轴测投影中,空间物体的三个(或一个)坐标轴是与投影面倾斜的,其投影就比原来的长度短。
为衡量其缩短的程度,我们把在轴测图中平行于轴测轴OX、OY、OZ的线段,与对应的空间物体上平行于坐标轴OX、OY、OZ的线段的长度之比,即物体上线段的投影长度与其实长之比,称为轴向伸缩系数(或称轴向变形系数)。
OX、OY、OZ三个方向上的轴向伸缩系数分别用p、q、r来表示,但常用p、q、r来表示111对应轴的简化的轴向伸缩系数(为简化作图,往往要规定其简化轴向伸缩系数,原来的叫实际轴向伸缩系数)。
在轴测投影中,由于确定空间物体的坐标轴以及投射方向与轴测投影面的相对位置不尽相同,因此轴测图可以有无限多种,得到的轴间角和轴向伸缩系数各不相同。
所以,轴间角和轴向伸缩系数是轴测图绘制中的两个重要参数。
5.1.3轴测轴的设置画物体的轴测图时,先要确定轴测轴,然后再根据该轴测轴作为基准来画轴测图。
轴测图中的三根轴测轴应配置成便于作图的位置,OZ轴表示立体的高度方向,应始终处于铅垂的位置,以便符合人们观察物体的习惯。
轴测轴可以设置在物体之外,但一般常设在物体本身内,与主要棱线、对称中心线或轴线重合。
绘图时,轴测轴随轴测图画出,也可省略不画。
.轴测图中,规定用粗实线画出物体的可见轮廓。
必要时,可用虚线画出物体的不可见轮廓。
5.1.4轴测投影的特点轴测投影仍是平行投影,所以它具有平行投影的一切属性。
(1)物体上互相平行的两条线段在轴测投影中仍然平行,所以凡与坐标轴平行的线段,其轴测投影必然平行于相应的轴测轴。
(2)物体上与坐标轴平行的线段,其轴测投影具有与该相应轴测轴相同的轴向伸缩系数,其轴测投影的长度等于该线段与相应轴向伸缩系数的乘积。
与坐标轴倾斜的线段(非轴向线段),其轴测投影就不能在图上直接度量其长度,求这种线段的轴测投影,应该根据线段两端点的坐标,分别求得其轴测投影,再连接成直线。
(3)沿轴测量性。
轴测投影的最大特点就是:必须沿着轴测轴的方向进行长度的度量,这也是轴测图中的“轴测”两个字的含义。
5.1.5轴测投影图的分类根据国家标准《技术制图—投影法》(GB/T14692—1993)中的介绍,轴测投影按投射方向是否与投影面垂直分为两大类,即:如果投射方向S与投影面P垂直(既使用正投影法),则所得到的轴测图叫做正轴测投影图,简称正轴测图。
如果投射方向S与投影面P倾斜(既使用斜投影法),则所得到的轴测图叫做斜轴测投影图,简称斜轴测图。
每大类再根据轴向伸缩系数是否相同,又分为三种:(1)若p=q=r,即三个轴向伸缩系数相同,称正(或斜)等测轴测图,简称正111(或斜)等测图。
(2)若有两个轴向伸缩系数相等,即p=q≠r或p≠q=r或r=p≠q,称正111111111(或斜)二等测轴测图,简称正(或斜)二测图。
(3)如果三个轴向伸缩系数都不等,即p≠q≠r,称正(或斜)三等测轴测111图,简称正(或斜)三测图。
国家标准中还推荐了三种作图比较简便的轴测图,即:正等测轴测图、正二等测轴测图、斜二等测轴测图三种标准轴测图。
工程上用的较多的是正等测图和斜二测图,本章将重点介绍正等测图的作图方法,简要介绍斜二测图的作图方法。
5.2正等测轴测图5.2.1正等测图的形成由正等测图的概念可知,其三个轴的轴向伸缩系数相等,即p=q=r。
因此,要想得到正等测轴测图,需将物体放置成使它的三个坐标轴与轴测投影面具有相同的夹角的位置,然后用正投影方法向轴测投影面投射,如图5-3所示,这样得到的物体的投影,就是其正等测轴测图,简称正等测图。
.PZOYXZO s YX5-3 正等测图的形成图5.2.2正等测图的参数1.轴间角因为物体放置的位置使得它的三个坐标轴与轴测投影面具有相同的夹角,所以正 YOX =120°。
在画图时,要将OZ轴画XOZ、ZOY、等测图的三个轴间角相等且成竖直位置,OX轴和OY轴与水平线的夹角都是30°,因此可直接用丁字尺和三角板作图,如图5-4a所示。
2.轴向伸缩系数正等测图的三个轴的轴向伸缩系数都相等,即p=q=r,所以在图5-3中的三个111轴与轴测投影面的倾角也应相等。
根据这些条件用解读法可以证明他们的轴向伸缩系数p=q=r≈0.82,如图5-4b 所示。
111Z1r OO q218=.00.=812p XYXY a)b)图5-4 正等测图的轴间角及轴向伸缩系数在画物体的轴测投影图时,常根据物体上各点的直角坐标,乘以相应的轴向伸缩系数,得到轴测坐标值后,才能进行画图。
因而画图前需要进行繁琐的计算工作。
当用p=q=r=0.82的轴向伸缩系数绘制物体的正等轴测图时,需将每一个轴向尺寸都111乘以0.82,这样画出的轴测图为理论的正等测轴测图,如图5-5a所示为一立体的三视图,用上述轴间角和轴向伸缩系数画出的该立体的正等测轴测图,如图5-5b所示。
为了简化作图,常将三个轴的轴向伸缩系数取为1,以此代替0.82,把系数1称为简化的轴向伸缩系数,OX、OY、OZ三个方向上简化后的轴向伸缩系数分别用p、q、r来表示。
运用简化后的轴向伸缩系数画出的轴测图与按实际的轴向伸缩系数画出的轴测投影图相比,形状无异,只是图形在各个轴向方向上放大了1/0.82≈1.22倍,如图5-5c所示。
ZZO O YX YX p=q=r=1p1=q1=r1=0.82c)b)a)图5-5理论的轴向伸缩系数与简化的轴向伸缩系数的比较5.2.3平面立体的正等测图的基本画法画轴测图的基本方法是坐标法。
但实际作图时,还应根据形体的形状特点的不同而灵活采用叠加和切割等其它作图方法,下面举例说明不同形状结构的平面立体轴测图的几种具体作图方法。
1.坐标法坐标法是根据形体表面上各顶点的空间坐标,画出它们的轴测投影,然后依次连接成形体表面的轮廓线,即得该形体的轴测图。
【例5-1】根据正六棱柱的主、俯视图(图5-6a所示),作出其正等测图。
x44F22oo E z Hef13213G xo431gh yc)a)b)ood)e)f)图5-6 用坐标法画正六棱柱的正等测图解:(1)分析首先要看懂两视图,想象出正六棱柱的形状大小。
由图5-6a可以看出,正六棱柱的前后、左右都对称,因此,选择顶面(也可选择底面)的中点作为坐标原点,并且从顶面开始作图。
(2)作图1)在正投影图上确定坐标系,选取顶面(也可选择底面)的中点作为坐标原点,,如图5-6a所示。
2)画正等测轴测轴,根据尺寸S、D定出顶面上的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个点,如图5-6b所示。
3)过Ⅰ、Ⅱ两点作直线平行于OX,在所作两直线上各截取正六边形边长的一半,得顶面的四个顶点E、F、G、H,如图5-6c所示。
4)连接各顶点如图5-6d所示。
5)过各顶点向下取尺寸H,画出侧棱及底面各边,如图5-6e所示。
6)擦去多余的作图线,加深可见图线即完成全图,如图5-6f所示。
2.叠加法叠加法也叫组合法,是将叠加式或以其它方式组合的组合体,通过形体分析,分解成几个基本形体,再依次按其相对位置逐个地画出各个部分,最后完成组合体的轴测图的作图方法。
【例5-2】根据平面立体的两视图,如图5-7a所示,画出它的正等测图。
zzzooxyyxxc)b)zxoyoyxa)e)d)图5-7用叠加法画平面立体的正等测解:(1)分析该平面立体可以看作是由3个四棱柱上下叠加而成,画轴测图时,可以由下而上(或者由上而下),也可以取两基本形体的结合面作为坐标面,逐个画出每一个四棱柱体。
(2)作图1)在正投影图上选择、确定坐标系,坐标原点选在基础底面的中心,如图5-7a所示。
x、y、z作出底部四棱柱的轴测图,如图5-7b所示。
2)画轴测轴。
根据111x、y作出中间四棱柱3)将坐标原点移至底部四棱柱上表面的中心位置,根据22z向上作出中间四棱柱的轴测图,如图5-7c底面的四个顶点,并根据所示。
2x、y作出上部四棱柱)将坐标原点再移至中间四棱柱上表面的中心位置,根据433z 5-7d所示。
底面的4个顶点,并根据向上作出上部四棱柱的轴测图,如图3所示。
5)擦去多余的作图线,加深可见图线即完成该基础的正等测,如图5-7e .切割法3切割法适合于画由基本形体经切割而得到的形体。
它是以坐标法为基础,先画出基本形体的轴测投影,然后把应该去掉的部分切去,从而得到所需的轴测图。
5-8a所示,用切割法绘制形体的正等测轴测图。
如图】【例5-3zzzxoooyyxxy d)b)c)a)图5-8 用切割法画轴测图解:(1)分析通过对图5-8a所示的物体进行形体分析,可以把该形体看作是由一长方体斜切左上角,再在前上方切去一个六面体而成。
画图时可先画出完整的长方体,然后再切去一斜角和一个六面体而成。
(2)作图1)确定坐标原点及坐标轴,如图5-8a所示。