当前位置：文档之家 › 八上数134最短路径问题(新)

八上数134最短路径问题(新)

  • 格式：ppt
  • 大小：574.50 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

2020最新初中数学人教版(新)八年级上134 课题学习 最短路径问题教案(1)

2020最新初中数学人教版(新)八年级上134 课题学习 最短路径问题教案(1)
4 / 10
l
现学生的合作 意识.
活动三：问题解决
1、作法： （1）作点B关于直线l的对称点B’. (2) 连接AB’，与直线l相交于点C. 则点C即为所求.
1、学生动手作图 ，并说明作图方 法.
2、比较不同作法 .
帮助学生比较 ，判断不同作 法的合理性， 让学生真正理 解解决问题的 方法.
*言念君 子，温 其如玉* 收集整 理，精 品资料 ，欢迎 下载使 用！
三、教学问题诊断分析
*言念君 子，温 其如玉* 收集整 理，精 品资料 ，欢迎 下载使 用！
2 / 10
最短路径问题从本质上说是极值问题，作为八年级的学生，在此之前很少接触
，解决这
方面问题的经验尚显不足，特别是面对具有实际背景的极值问题，更会感到陌
生，无从下手
对于直线同侧的两点，如何在直线上找到一点，使这一点到这两点的距离
之和最小，
一些学生会感到茫然，找不到解决问题的思路．教学时．教师可从“直线异侧
的两点”过渡到“直线同侧的两点”，为学生搭建“脚手架”．
在证明“最短”时，需要在直线上任取一点（与所求作的点不重合），证明
所连线段和
大于所求作的线段和，学生想不到，不会用．教师可作适时的点拨，让学生体
会“任意”的作用.
基于以上分析，确定本节课的教学难点是：如何利用轴对称、平移变化将
学生通过观察 分析，体会实 际问题数学化 的过程，同时 也培养学生的 模型思想.
活动二：自主探究 问题1 如图，点A，B 在直线l 的同侧，点C 是直 线上的一个动点，当点C 在l 的什么位置时，AC 与CB 的和最小？
如果学生有困难，适时提示： （1） 如果点B在点A的异侧，如何在直
线l上找到一点C，使AC与BC的和 最小

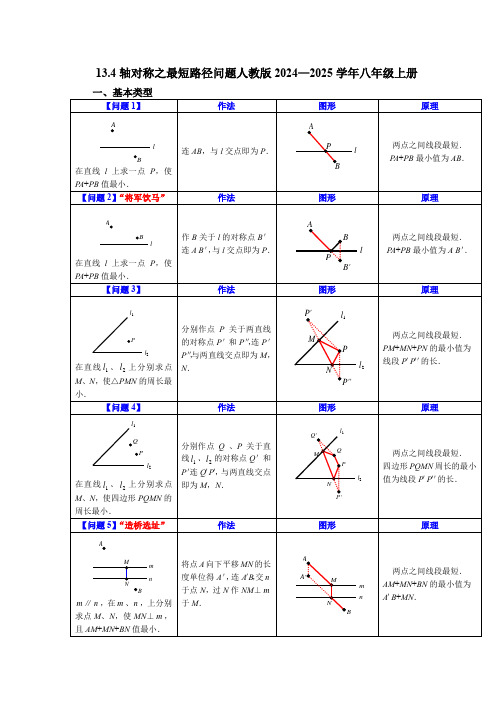
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册

13.4轴对称之最短路径问题人教版2024—2025学年八年级上册

13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。

人教版八年级数学上册同步练习13.4 课题学习 最短路径问题(word版,含答案解析)

人教版八年级数学上册同步练习13.4 课题学习 最短路径问题(word版,含答案解析)

人教版八年级数学上册13.4 课题学习最短路径问题一、选择题（共16小题；共80分）1. 如图，直线是一条河，，是两个村庄．欲在上的某处修建一个水泵站，向，两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是A. B.C. D.2. 如图，四边形是直角梯形，，，点是腰上的一个动点，要使最小，则点应该满足A. B.C. D.3. 四边形中，，，在，上分别找一点，，使三角形周长最小时，则的度数为A. B. C. D.4. 如图，直线外存在不重合的两点，，在直线上求作一点，使得的长度最短，作法为：① 作点关于直线的对称点；②连接与直线相交于点，则点为所求作的点．在解决这个问题时没有运用到的知识或方法是A. 转化思想B. 三角形的两边之和大于第三边C. 两点之间，线段最短D. 三角形的一个外角大于与它不相邻的任意一个内角5. 如图，牧童在处放牛，其家在处，，到河岸的距离分别为和，且，若点到河岸的中点的距离为米，则牧童从处把牛牵到河边饮水再回家，最短距离是A. 米B. 米C. 米D. 米6. 如图，已知直线，且与之间的距离为，点到直线的距离为，点到直线的距离为，．试在直线上找一点，在直线上找一点，满足且的长度最短，则此时A. B. C. D.7. 如图，正的边长为，过点的直线，且与关于直线对称，为线段上一动点，则的最小值是A. B. C. D.8. 如图，在中，，，是的两条中线，是上一个动点，则下列线段的长度等于最小值的是A. B. C. D.9. 如图，在四边形中，，，在，上分别找一点，，使的周长最小，此时，A. B. C. D.10. 如图，，内有一定点，且，在上有一动点，上有一动点．若周长最小，则最小周长是A. B. C. D.11. 如图，四边形中，，，，分别是，上的点，当的周长最小时，的度数为A. B. C. D.12. 如图，在中，，，面积是，的垂直平分线分别交，边于，点．若点为边的中点，点为线段上一动点，则周长的最小值为A. B. C. D.13. 如图，在中，，，，为上一点，且，平分交于．若是上的动点，则的最小值等于A. B. C. D.14. 如图，圆柱形容器高为，底面周长为，在杯内壁离杯底的点处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿与蜂蜜相对的点处，则蚂蚁从外壁处到达内壁处的最短距离为A. C. D.15. 如图，点是内任意一点，且，点和点分别是射线和射线上的动点，当周长取最小值时，则的度数为A. B. C. D.16. 如图，，点是内任意一点，，点和点分别是射线和射线上的动点，若周长的最小值是，则的值是A. B. C. D.二、填空题（共5小题；共25分）17. 与的最小公倍数是．18. 如图，在中，是边的中点，过点作边的垂线，是上任意一点，且，，则的周长的最小值为．19. 如图，在中，，，的垂直平分线交于点，交于点，在直线上存在一点，使，，三点构成的的周长最小，则的周长最小值为．20. 已知，点在的内部，点是边上任意一点，点是边上任意一点，连接，，当的周长最小时，的度数为．21. 如图，是等腰直角三角形，，，为上的动点，则的最大值为．三、解答题（共3小题；共45分）22. 如图，已知直线及其同侧两点，，在直线上找一点，使得的长度最小．23. 如图，点，在的内部，为射线上的一个动点，为射线上的一个动点，求作点，，使得的长最短．作法：24. 如图，，两个小集镇在河流的同侧，分别到河的距离为千米，千米，且千米，现在要在河边建一自来水厂，向，两镇供水，铺设水管的费用为每千米万，请你在河流上选择水厂的位置，使铺设水管的费用最节省，并求出总费用是多少?答案第一部分1. D2. D 【解析】如图，作点关于的对称点，连接交于，连接．根据轴对称的性质，得，根据对顶角相等知，所以．3. C4. D5. B6. B7. A 【解析】如图所示.过点作的对称点，连接，与的延长线交于点 .此时，为最小值 .点在线段上，点在点处.的最小值为．8. B 【解析】如图连接，，，，，，，，，共线时，的值最小，最小值为的长度．9. D10. B【解析】设，则，作与相交于，并将延长一倍到，即，作与相交于，并将延长一倍到，即，连接与相交于，与相交于，再连接，，连接，，则即为周长最短的三角形，是的垂直平分线，；同理，是的垂直平分线，，的周长，，且，是等边三角形，，即在保持的条件下的最小周长为．11. D 【解析】作关于和的对称点，，连接，交于，交于，则即为的周长最小值．作延长线 .，...，，..12. C 【解析】连接．是等腰三角形，点是边的中点，，，解得，是线段的垂直平分线，点关于直线的对称点为点，的长为的最小值，13. D 【解析】如图，作点关于的对称点，连接交于，连接，此时的值最小，作于．，，，，，，，，，故选：D．14. D 【解析】如图：将杯子侧面展开，作关于的对称点，连接，则即为最短距离，．15. B【解析】分别作点关于，的对称点，，连接，分别交，于点，，如图所示：此时的周长取最小值．，，，，，，，．16. B第二部分17.18.19.【解析】如图，连接．，，的值最小时，的周长最小，垂直平分线段，，，的最小值为，的周长的最小值为．20.【解析】如图，过点作关于，的对称点，，连接，与，相交与点，，则此时的周长最小，为线段的长度；，，，，，，，，，，，解得：；故答案为：．21.第三部分22. 过点作直线的垂线，垂足为点，截取，连接，则与的交点就是点．23. 作点关于直线的对称点，作点关于直线的对称点交于，交于，则最短．24. 作关于的对称点，连接交于，点即为所求作的点，则可得：（千米），所以（千米），所以（千米），总费用为万元．。

人教版八年级数学上册13.4最短路径问题优秀教学案例

人教版八年级数学上册13.4最短路径问题优秀教学案例
3.小组合作学习：教师将学生分成小组，鼓励学生进行合作交流，共同探讨最短路径问题的解决方法。通过小组合作，学生可以互相学习、互相借鉴，提高解决问题的能力，同时培养团队合作精神和沟通能力。
4.多媒体教学手段：利用多媒体教学手段，如图片、视频等，展示实际问题情境，让学生更直观地感受到问题的背景和意义，提高学习效果。
在现实生活中，最短路径问题具有广泛的应用，如道路规划、网络路由等。因此，本节课的教学案例将以实际问题为背景，引导学生运用数学知识解决实际问题，培养学生的数学应用意识。
为了提高教学效果，本节课将采用小组合作、讨论交流的教学方法，让学生在探讨最短路径问题的过程中，提高自主学习能力和合作意识。同时，教师将以引导者、组织者的角色参与教学，为学生提供必要的帮助和指导，确保教学活动的顺利进行。
（三）小组合作
1.教师将学生分成小组，鼓励学生进行合作交流，共同探讨最短路径问题的解决方法。
2.教师引导学生进行小组讨论，鼓励学生分享自己的思路和观点，培养学生的合作意识和团队精神。
3.教师巡回指导，参与小组讨论，为学生提供必要的帮助和指导，确保每个学生都能参与到教学活动中来。
（四）反思与评价
1.教师引导学生进行自我反思，总结自己在解决最短路径问题过程中的思路和方法，找出自己的不足之处。
3.教师介绍迪杰斯特拉算法和贝尔曼-福特算法，讲解这两种算法的原理和步骤，并通过示例进行演示。
4.教师引入动态规划思想，讲解如何运用动态规划解决最短路径问题，并给出动态规划解决最短路径问题的步骤。
（三）学生小组讨论
1.教师将学生分成小组，并提出讨论问题，如“比较迪杰斯特拉算法和贝尔曼-福特算法的优缺点”、“如何运用动态规划解决最短路径问题？”等。
2.利用多媒体教学手段，展示实际问题情境，让学生直观地感受到最短路径问题的重要性和实用性。

人教版数学八年级上册13.4课题学习最短路径问题将军饮马优秀教学案例

人教版数学八年级上册13.4课题学习最短路径问题将军饮马优秀教学案例
（二）过程与方法
在本章节的学习过程中，学生将经历以下过程与方法：
1.通过小组合作、讨论交流的方式，培养学生的团队协作能力和沟通能力。
2.引导学生从实际问题出发，培养学生的发现问题、分析问题和解决问题的能力。
3.利用数学软件、教具等辅助工具，培养学生的动手操作能力和实际应用能力。
4.通过对最短路径问题的探讨，引导学生掌握数学建模的方法，提高学生的数学思维能力。
4.教师巡回指导，关注每个小组的学习情况，及时解答学生疑问。
（四）反思与评价
1.教师引导学生对所学知识进行总结、反思，帮助学生巩固知识点，形成知识体系。
2.鼓励学生自我评价，反思自己在解决问题过程中的优点和不足，培养学生的自我认知能力。
3.组织小组互评，让学生学会欣赏他人的优点，发现自身的不足，促进团队合作。
3.对学生提出的解决方案进行讨论、分析，找出最优解，并解释其原理。
（三）小组合作
小组合作是实现教学目标的重要途径，具体策略如下：
1.将学生分成若干小组，每组4-6人，确保组内成员在知识、能力、性格等方面具有一定的互补性。
2.各小组针对问题进行讨论、研究，共同寻找解决方案。
3.小组间进行交流、分享，互相学习，取长补短。
4.教师对学生在课堂上的表现进行评价，给予肯定和鼓励，指出需要改进的地方。
（五）作业小结
在作业小结环节，我将布置以下任务：
1.请学生运用所学知识，解决一个生活中的最短路径问题，并以作文或报告的形式提交。
2.要求学生在作业中阐述自己的思考过程、解决方案和心得体会，以提高学生的书面表达能力。
3.鼓励学生进行课后拓展，了解其他求解最短路径的方法，如：A*算法、遗传算法等，提升学生的自主学习能力。
3.小组间进行分享、交流，互相借鉴，完善各自的方法和思路。

2023-2024学年人教版八年级数学上学期：课题学习 最短路径问题(附答案解析)

2023-2024学年人教版八年级数学上学期：课题学习 最短路径问题(附答案解析)

第1页（共9页）
2023-2024学年人教版八年级数学上学期13.4课题学习 最短路
径问题
一．选择题（共6小题）
1．如图，点P 为∠AOB 内一点，分别作点P 关于OA ，OB 的对称点P 1，P 2，连接P 1，P 2
交OA 于M ，交OB 于N ，若P 1P 2＝6，则△PMN 周长为（ ）
A ．4
B ．5
C ．6
D ．7
2．如图，直线L 是一条输水主管道，现有A 、B 两户新住户要接水入户，图中实线表示铺
设的管道，则铺设的管道最短的是（ ）
A ．
B ．
C ．
D ．
3．如图，直线l 是一条河，P ，Q 是两个村庄．计划在l 上的某处修建一个水泵站M ，向P ，
Q 两地供水．现有如下四种铺设方案（图中实线表示铺设的管道），则所需管道最短的是（ ）
A ．
B ．
C ．
D ．
4．如图，直线m 表示一条河，M ，N 表示两个村庄，欲在m
上的某处修建一个给水站，向。

八年级数学上册 13.4 课题学习 最短路径问题教学设计 (新版)新人教版

八年级数学上册 13.4 课题学习最短路径问题教学设计（新版）新人教版一. 教材分析“课题学习最短路径问题”是人教版八年级数学上册第13.4节的内容。

这部分内容主要让学生了解最短路径问题的实际应用，学会使用图论中的最短路径算法来解决实际问题。

教材通过引入一个实际问题，引导学生探讨并找出解决问题的方法，从而培养学生解决问题的能力和兴趣。

二. 学情分析八年级的学生已经掌握了图论的基本知识，如图的定义、图的表示方法等。

但是，对于图的最短路径问题，学生可能还没有直观的理解和认识。

因此，在教学过程中，教师需要结合学生的已有知识，通过实例讲解、动手操作等方式，帮助学生理解和掌握最短路径问题。

三. 教学目标1.知识与技能目标：让学生了解最短路径问题的实际应用，学会使用图论中的最短路径算法来解决实际问题。

2.过程与方法目标：通过探讨实际问题，培养学生解决问题的能力和兴趣。

3.情感态度与价值观目标：培养学生对数学的热爱，提高学生解决实际问题的能力。

四. 教学重难点1.教学重点：最短路径问题的实际应用，图论中的最短路径算法。

2.教学难点：如何引导学生从实际问题中抽象出最短路径问题，并运用图论知识解决。

五. 教学方法1.情境教学法：通过引入实际问题，激发学生的学习兴趣，引导学生主动探究。

2.实例讲解法：通过具体的实例，讲解最短路径问题的解决方法，帮助学生理解和掌握。

3.动手操作法：让学生亲自动手操作，加深对最短路径问题的理解。

六. 教学准备1.教学素材：准备一些实际问题的案例，以及相关的图论知识介绍。

2.教学工具：多媒体教学设备，如PPT等。

3.学生活动：让学生提前预习相关内容，了解图论的基本知识。

七. 教学过程1.导入（5分钟）通过一个实际问题引入最短路径问题，激发学生的学习兴趣。

例如，讲解从一个城市到另一个城市，如何找到最短的路线。

2.呈现（15分钟）讲解最短路径问题的定义，以及图论中最短路径算法的基本原理。

通过PPT等教学工具，展示相关的知识点，让学生直观地了解最短路径问题。

人教版八年级数学上册《134课题学习最短路径问题》优秀教学案例

2.培养学生运用数学知识解决实际问题的能力，能够将所学的最短路径问题应用到生活中，提高学生的数学应用意识。
3.通过解决最短路径问题，使学生了解数学与现实生活的紧密联系，培养学生的数学素养。
在教学过程中，我将以生活中的实际问题为载体，引导学生理解和掌握最短路径问题的基本概念。通过设计具有层次性的问题，让学生在解决问题的过程中，逐步掌握解决最短路径问题的方法。同时，我还将结合实例，使学生能够将所学的知识应用到实际问题中，提高学生的数学应用能力。
（三）学生小组讨论
在讲授新知后，我将组织学生进行小组讨论。我会提出几个具有挑战性的问题，让学生以小组为单位进行讨论和解决。例如：如何在给定的坐标系中找到两点之间的最短路径？如何利用函数图象分析最短路径问题？通过小组讨论，培养学生的团队协作能力和沟通能力，使学生能够将所学的知识应用到实际问题中。
（四）总结归纳
在学生小组讨论后，我将引导学生进行总结归纳。我会让学生分享他们在讨论中得到的解决方案，并对这些方案进行分析和评价。通过总结归纳，使学生能够更好地理解和掌握最短路径问题的解决方法，并能够将其应用到实际问题中。
（五）作业小结
在本节课的最后，我会布置一个相关的作业，让学生课后进行练习。作业的内容将包括本节课所学的最短路径问题的解决方法，以及一些实际问题的应用。通过作业小结，巩固学生所学的知识，提高学生的数学应用能力。
4.反思与评价：我引导学生进行自我反思，养成自我反思的好习惯。同时，我还会在课堂上组织学生进行互评和小组评价，使学生能够更好地了解自己的优点和不足，提高自己的学习能力。此外，我还注重对学生进行形成性评价，关注学生在学习过程中的表现，及时给予反馈，激发学生的学习兴趣，提高学生的学习积极性。
5.教学内容与过程：本节课的教学内容与过程紧密联系实际，具有较高的实用性和针对性。在教学过程中，我充分尊重学生的认知规律，注重引导学生主动探究，激发学生的学习兴趣。通过本节课的学习，学生不仅能够理解和掌握最短路径问题的解决方法，还能够将所学的知识应用到实际问题中，提高学生的数学应用能力。

八年级上学期数学134《最短路径问题》课件


·
E
2/23/2019
14
(Ⅲ)一点在两相交直线内部
已知：如图A是锐角∠MON内部任意一点，在∠MON的两 边OM，ON上各取一点B，C，组成三角形，使三角形周 长最小. 分析：当AB、BC和AC三条边的长度恰好能够体现在 一条直线上时，三角形的周长最小
D
B C
E
2/23/2019 15
(Ⅲ)一点在两相交直线内部
6
即MA + MB′>PA+PB
2/23/2019
三角形任意两边之和大于第三边
练习
问题：如图所示，要在街道旁修建一个奶站， 向居民区A、B提供牛奶，奶站应建在什么地方， 才能使从A、B到它的距离之和最短．
请你自己动手 试一试！
2/23/2才能使AC+BC最小．作点 A关于直线“街道”的对称点A′，然后连接A′B，交“街 道”于点C，则点C就是所求的点．
B
2/23/2019
11
• 4. 如图：C为马厩，D为帐篷，牧马人某一天要从马厩牵出马，
先到草地边某一处牧马，再到河边饮马，然后回到帐篷，请你 帮他确定这一天的最短路线。
作法：1.作点C关于直线
OA 的 对称点点F, G A 2. 作点D关于直线 OB ·C 的对称点点E, 3.连接EF分别交直线OA.OB于点G.H， D · 则CG+GH+DH最短
2/23/2019
9
1. 如图，A.B两地在一条 河的两岸，现要在河上建 一座桥MN，桥造在何处 才能使从A到B的路径 AMNB最短？（假设河的 两岸是平行的直线，桥要 与河垂直）
A·
·B
2/23/2019 10
作法：1.将点B沿垂直与河岸的方向平移一个河宽到E， 2.连接AE交河对岸与点M, 则点M为建桥的位置，MN为所建的桥。 证 明 ： 由 平 移 的 性 质 ， 得 BN∥EM 且 BN=EM, MN=CD, BD∥CE, BD=CE, 所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在CD处，连接AC.CD.DB.CE, A· M C 则AB两地的距离为： AC+CD+DB=AC+CD+CE=AC+CE+MN, 在△ACE中，∵AC+CE＞AE, N D ∴AC+CE+MN＞AE+MN, E 即AC+CD+DB ＞AM+MN+BN 所以桥的位置建在CD处，AB两地的路程最短。

人教版初中数学八年级上册13.4最短路径问题(教案)

（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与最短路径相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。这个操作将演示最短路径的基本原理。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“最短路径在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《最短路径问题》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过如何找到两点间最短距离的情况？”（如从家到学校的最短路线）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索最短路径的奥秘。
（3）在复杂图形中寻找最短路径时，可以引导学生从简单图形出发，逐步增加难度，让学生掌握解题方法；
（4）结合实际应用，可以设计一些案例，如旅行商问题、工程选址问题等，指导学生如何将所学知识运用到实际中。
在教学过程中，教师应针对这些难点和重点，运用生动形象的语言、具体实例和操作演示，帮助学生理解、掌握和运用相关知识。同时，注意关注学生的反馈，适时调整教学方法和进度，确保学生透彻理解本节课的核心内容。
（3）在实际图形中寻找最短路径，如三角形、四边形等；
（4）将现实生活中的问题转化为数学模型，利用数学知识求解。
举例：讲解最短路径概念时，可以通过实际生活中的例子（如地图上两点间的最短距离）进行说明，使学生理解并掌握这个核心概念。
2.教学难点
（1）如何将实际问题抽象为数学模型，找到最短路径；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B′
A、B同侧
由特殊到一般
反馈拓展
如图，一个旅游船从大桥AB的P处前往山脚下的Q处接 游客，然后将游客送往河岸BC上，再回到P处，请画出旅 游船的最短路径。
D
P′
最短路径问题
P
B′
转化思想
C
D
P′
课后作业 相传，古希腊亚历山大里亚城里有一位久
负盛名的学者，名叫海伦．有一天，一位将军专程拜访 海伦，求教一个百思不得其解的问题：
从图中的A 地出发，到一条笔直的河边l 饮马，然 后到B 地．到河边什么地方饮马可使他所走的路线全程 最短？
B A
l
变 式 将军饮马
l1 l2
C A′
D B′
A B
必做题
1、如图：一牧童在A处饮马，牧童家在B 处，A、B处距河岸有一定的距离。天黑前 牧童从A点将马牵到河边去饮水，再赶回家， 你能知道牧童怎样走路程最短吗？
C
A、B异侧
A、B同侧
意见2： 作点B关于直 线l的对称点， 如图AC+BC最
短。
意见1:
垂线段最短， 所以AC+BC最
短。
猜想：AC′+BC′ ＞ AC+BC
猜想：AC′+BC′
AC+BC
C′
互动释疑
验证：在直线l 上任取一点C′（与点C 不重合），连接
AC′，BC′，B′C′．你能用所学的知识证明AC +BC最短 吗？
C D
．
B．
A
选做题
2、 如图：为了做好国庆期间的交通安全工作，
某交警执勤小队从A处出发，先到公路 上l设1
卡检查，然后到公路 上设l2卡检查，最后再到
达B地执行任务。他们如何走才能使其总路程
最短？
l1 l2
C A′
D B′
A B
作业
课本93页：15题
问题：济源正在进行天燃气管道改造（如图)。 现需要向A、B两个小区供气，问：当A、B同侧时， 泵站应修在主管道L的什么地方，可使所用的输 气管线最短？
证明：
由轴对称的性质知，
BC = ，BC′= ．
∴ AC +BC=
，
AC′+BC′=
+
．
在△AB′C′中 ＜AC′+B′C′
∴ AC +BC＜AC′+BC′ 即 AC +BC 最短
A
·
C′ C
B
·
l B′
归纳提升：
回顾前面的探究过程，我们通过怎样的过 程、借助什么方法来解决问题的？
C
P
A、B异侧
做对称点 转化思想
济水一中 蒋燕萍
蚂蚁 A
食物
B
A
C P B
D
问题：济源正在进行天燃气管道改造（如
图)。现需要向A、B两个小区供气，问：当 A、B异侧时，泵站应修在主管道L的什么地 方，可使所用的输气管线最短？
C
问题：济源正在进行天燃气管道改造（如
图)。现需要向A、B两个小区供气，问：当 A、B同侧时，泵站应修在主管道L的什么地 方，可使所用的输气管线最短？
C
A