13.4最短路径问题

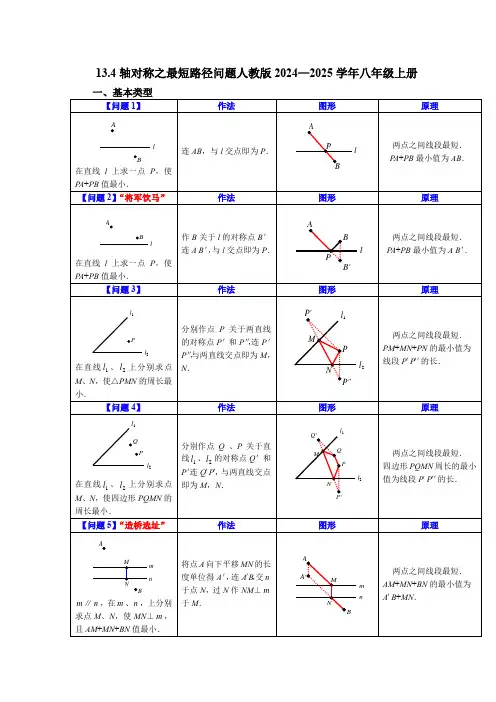
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。

13.4 课题学习最短路径问题一、解决“一线＋两点”型最短路径问题的方法：(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求．如图所示，点A，B分别是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短，这时点C是直线l与AB的交点．(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，则与该直线的交点即为所.例题1：在图中直线l上找到一点M，使它到A，B两点的距离和最小．注意：距离之和最小问题的基本思路，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同．【练习】如图，小河边有两个村庄A，B，要在河边建一自来水厂向A村与B村供水．(1)若要使厂部到A，B村的距离相等，则应选择在哪建厂？(2)若要使厂部到A，B两村的水管最短，应建在什么地方？警误区：利用轴对称解决最值问题应注意题目要求：根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法．解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问．二、解决“两线＋一点”型最短路径问题的方法：解决“两线＋一点”型最短路径问题，要作两次轴对称，从而构造出最短路径．例题2：如图，已知∠AOB内有一点P，试分别在边OA和OB上各找一点E、F，使得△PEF的周长最小。

试画出图形，并说明理由.三、解决“两线＋两点”型最短路径问题的方法：解决“两线＋两点”型最短路径问题，要每点做一次轴对称，从而构造出最短路径．例题3：圣林中学八年级举行元旦联欢会，桌子摆成如图a所示两直排(图中的AO，BO)，AO桌面上摆满了橘子，OB桌面上摆满了糖果，站在C处的学生小明先拿橘子再拿糖果，然后到D处座位上，请你帮助他设计一条行走路线，使其所走的总路程最短？图a四、造桥选址问题：选址问题的关键是把各条线段转化到一条线段上．解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．例题4：如图，村庄A、B位于一条小河的两侧，若河岸a、b彼此平行，现在要建设一座与河岸垂直的桥CD，问桥址应如何选择，才能使A村到B村的路程最近？注：在解决最短路径问题时，我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上，从而作出最短路径的方法来解决问题．。

13.4 课题学习 最短路径问题学习目标：1.利用“两点之间，线段最短”，“连接直线外一点与直线上各点的所有线段中，垂线段最短”来解决有关的最短路径问题.2.学会运用轴对称、平移把已知问题转化为容易解决的问题，从而解决最短路径问题. 一、学前准备1.如图，在Rt △ABC 中，CD 是斜边AB 上的高，∠B =30°，AD =2 cm ，则AB 的长度是（ ） A .2 cmB .4 cmC .8 cmD .16cm2.如图所示，从A 地到B 地有三条路可供选择，你会选走哪条路最近？你的理由是什么？二、预习导航 （一）预习指导活动1 探究牧马人饮马问题（阅读教材第85～86页，运用轴对称解决牧马人饮马问题） 3.（两点在一条直线异侧）如图，点A 、点B 在直线的两侧，请你在上找一个点P ，使得这个点到点A 、B 的距离和最短，即PA +PB 最小. 思考：为什么这样做就能得到最短距离呢？你如何验证PA +PB 最短呢？lAB第1题图BA CD第2题图4.（两点在一条直线同侧）问题：如图，牧马人从A 地出发，到一条笔直的河边饮马，然后到B 地.牧马人到河边的什么地方饮马，可是所走的路径最短？（提示：这个问题可以转化为：当点C 在的什么位置时，AC 与BC 的和最小？）活动2 探究造桥选址问题（阅读教材第86～87页，运用平移解决造桥选址问题） 5.如图所示，在一条河的两岸有两个村庄A 和B ，现要在河上建一座小桥，桥的方向与河流垂直，设河的宽度不变，试问：桥架在何处，才能使从A 到B 的距离最短？归纳：造桥选址问题是利用__________将问题转化为__________________________的问题. 预习疑惑： （二）预习检测6.如图，在正方形ABCD 中，点M 在DC 上，点N 是AC 上一动点，当N 在________和AC 的交点处时，DN +MN 的值最小.三、课堂互动 问题1最短路径问题7.如图，牧童在A 处放牛，其家在B 处，A ，B 到河岸的距离分别为AC ，BD ，且AC =BD ，若A 到河岸CD 的中点的距离为500 m .问：lABa bAB（1）牧童从A处把牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？（2）最短路程为多少？方法总结：四、总结归纳1. 你有什么收获？（从知识、方法、规律方面总结）2. 你还有哪些疑惑？3. 你认为老师上课过程中还有哪些需要注意或改进的地方？4. 在展示中，哪位同学是你学习的榜样？哪个学习小组的表现最优秀？教（学）后记：五、达标检测1.如图，直线l是一条河，A、B两地相距5 km，A，B两地到l的距离分别为3 km，6 km，欲在l上的某点M处修建一个水泵站，向A，B两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（）A.B.C.D.2.如图，已知等边△ABC的边长为6，点D为AC的中点，点E为BC的中点，点P为BD 上一点，则PE+PC的最小值为（）A.3B.3C.2D.333.如图，A，B两个电话分机到电话线l的距离分别是3 m，5 m，CD=6 m，若由l上一点分别向A，B连电话线，最短应为（）A.8 mB.9 mC.10 mD.11 m4.如图，在矩形ABCD中，点E为BC的中点，点F在C D上，要使△AEF的周长最小时，确定点F的位置的方法为．《13.4 课题学习 最短路径问题》参考答案一、学前准备 1.答案：C.2.答案：②，理由：两点之间，线段最短. 二、预习导航3.略.4.略.5.略.归纳：平移；两点之间，线段最短. 6.答案：BM . 三、课堂互动7.解：（1）作点A 关于CD 的对称点A′，连接A′B ，交CD 于M .则点M 为饮水处，线段A′B 的长度即为牧童从A 处把牛赶到河边饮水后回家，所走的最短路程； （2）连接AM .∵点A 关于CD 的对称点是A′，点M 在CD 上， ∴A′C =AC ，A′M =AM . ∵AC =DB ， ∴A′C =BD .∵AC ⊥CD ，BD ⊥CD ， ∴∠ACD =∠A′CD =∠BDC =90°. ∵在△CA′M 和△DBM 中，'''A CM BDM A MC BMD A C BD ∠=∠∠=∠=⎧⎪⎨⎪⎩∴△CA′M ≌△DBM . ∴A′M =BM ，CM =DM . ∴M 为CD 中点.∴BM=AM=500（米）∴A′B=A′M+BM=AM+BM=1000（米）即最短路程是1000米.五、达标检测1.答案：A.2.答案：D.3.答案：C.4.答案：作点E关于DC的对称点E′，连接AE′交CD于点F.。

专题13.4 最短路径问题1．最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求．如图所示，点A，B分别是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短，这时点C是直线l与AB的交点．(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，则与该直线的交点即为所求．如图所示，点A，B分别是直线l同侧的两个点，在l上找一个点C，使CA＋CB最短，这时先作点B关于直线l的对称点B′，则点C是直线l与AB′的交点．为了证明点C的位置即为所求，我们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′，证明AC ＋CB＜AC′＋C′B.如下：证明：由作图可知，点B和B′关于直线l对称，所以直线l是线段BB′的垂直平分线．因为点C与C′在直线l上，所以BC＝B′C，BC′＝B′C′.在△AB′C′中，AB′＜AC′＋B′C′，所以AC＋B′C＜AC′＋B′C′，所以AC＋BC＜AC′＋C′B.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题的基本思路，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同．利用轴对称解决最值问题应注意题目要求根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法．解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问．3．利用平移确定最短路径选址选址问题的关键是把各条线段转化到一条线段上．如果两点在一条直线的同侧时，过两点的直线与原直线的交点处构成线段的差最大，如果两点在一条直线的异侧时，过两点的直线与原直线的交点处构成的线段的和最小，都可以用三角形三边关系来推理说明，通常根据最大值或最小值的情况取其中一个点的对称点来解决．解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．在解决最短路径问题时，我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上，从而作出最短路径的方法来解决问题．4．生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知，求距离之和最小问题，就是运用等量代换的方式，把几条线段的和想办法转化在一条线段上，从而解决这个问题，运用轴对称性质，能将两条线段通过类似于镜面反射的方式转化成一条线段，如图，AO＋BO＝AC的长．所以作已知点关于某直线的对称点是解决这类问题的基本方法．5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键．先做出其中一点关于对称轴的对称点，然后连接对称点和另一个点，所得直线与对称轴的交点，即为所求．根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值．破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法．【例题1】在图中直线l上找到一点M，使它到A，B两点的距离和最小．【答案】见解析。