【高考调研】2015高中数学 1-2 排列与组合2课后巩固 新人教A版选修2-3

课时跟踪检测(六十三)排列与组合第Ⅰ组：全员必做题1．(2013·开封模拟)把标号为1,2,3,4,5的同色球全部放入编号为1～5号的箱子中，每个箱子放一个球且要求偶数号的球必须放在偶数号的箱子中，则所有的放法种数为() A．36B．20C．12 D．102．(2013·昆明重点高中检测)某班班会准备从含甲、乙的7名学生中选取4人发言，要求甲、乙2人至少有一人参加，若甲、乙同时参加，则他们发言时顺序不能相邻，那么不同的发言顺序种数为()A．720 B．520C．600 D．3603．(2013·昆明调研)航空母舰“辽宁舰”将进行一次编队配置科学试验，要求2艘攻击型核潜艇一前一后，3艘驱逐舰和3艘护卫舰分列左右，每侧3艘，同侧不能都是同种舰艇，则舰艇分配方案的方法数为()A．72 B．324C．648 D．1 2964．(2013·合肥调研)身穿红、黄两种颜色衣服的各有两人，身穿蓝色衣服的有一人，现将这五人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法种数为() A．24 B．28C．36 D．485．(2014·大连模拟)把五个标号为1到5的小球全部放入标号为1到4的四个盒子中，不许有空盒且任意一个小球都不能放入标有相同标号的盒子中，则不同的放法有() A．36种B．45种C．54种D．96种6．(2014·哈师大附中模拟)将4名实习教师分配到高一年级的3个班实习，若每班至少安排1名教师，则不同的分配方案种数为()A．12 B．36C．72 D．1087．(2013·广州调研)某高校从5名男大学生志愿者和4名女大学生志愿者中选出3名派到3所学校支教(每所学校一名志愿者)，要求这3名志愿者中男、女大学生都有，则不同的选派方案共有()A．210种B．420种C．630种D．840种8．(2013·开封模拟)2位男生和3位女生共5位同学站成一排，若男生甲不站两端，3位女生中有且只有两位女生相邻，则不同排法的种数是()A．60 B．48C．42 D．369．(2014·潍坊检测)张、王两家夫妇各带1个小孩一起到动物园游玩，购票后排队依次入园．为安全起见，首尾一定要排两位爸爸，另外，两个小孩一定要排在一起，则这6人的入园顺序排法种数为________．(用数字作答)10．(2013·石家庄模拟)有4名同学参加唱歌、跳舞、下棋三项比赛，每项比赛至少有1人参加，每名同学只参加一项比赛，另外甲同学不能参加跳舞比赛，则不同的参赛方案的种数为________(用数字作答)．11．某公司计划在北京、上海、广州、南京4个候选城市投资3个不同的项目，且在同一个城市投资的项目不超过2个，则该公司不同的投资方案种数是________(用数字作答)．12．(2014·重庆模拟)将7个相同的球放入4个不同的盒子中，则每个盒子都有球的放法共有________种．第Ⅱ组：重点选做题1．从1到9的9个数字中取3个偶数4个奇数，试问：(1)能组成多少个没有重复数字的七位数？(2)上述七位数中，3个偶数排在一起的有几个？(3)(1)中的七位数中，偶数排在一起，奇数也排在一起的有几个？2．有4个不同的球，4个不同的盒子，把球全部放入盒内．(1)恰有1个盒不放球，共有几种放法？(2)恰有1个盒内有2个球，共有几种放法？(3)恰有2个盒不放球，共有几种放法？答案第Ⅰ组：全员必做题1．选C依题意，满足题意的放法种数为A22·A33＝12，选C.2．选C根据题意，分2种情况讨论：若甲、乙其中一人参加，有C12·C35·A44＝480种；若甲、乙2人都参加，共有C22·C25·A44＝240种发言顺序，其中甲、乙相邻的情况有C22·C25·A22·A33＝120种，故有240－120＝120种．则不同的发言顺序种数为480＋120＝600.3．选D核潜艇排列数为A22，6艘舰艇任意排列的排列数为A66，同侧均是同种舰艇的排列数为A33A33×2，则舰艇分配方案的方法数为A22(A66－A33A33×2)＝1 296.4．选D穿红色衣服的人相邻的排法有C14A22A33＝48种，同理穿黄色衣服的人相邻的排法也有48种．而红色、黄色同时相邻的有A22·A22·A33＝24种．故穿相同颜色衣服的不相邻的排法有A55－2×48＋24＝48种．5．选A先把5号球放入任意一个盒子中有4种放法，再把剩下的四个球放入盒子中，根据4的“错位数”是9，得不同的放法有4×9＝36种．6．选B本题是定向分配问题．由于元素个数多于位置个数，故先分堆再分位置，分两步完成，第一步，从4名教师中选出2名教师分成一组，其余2名教师各自为一组，共有C24种选法，第二步，将上述三组与3个班级对应，共有A33种，这样，所求的不同的方案种数为C24A33＝36.7．选B从这9名大学生志愿者中任选3名派到3所学校支教，则有A39种选派方案，3名志愿者全是男生或全是女生的选派方案有A35＋A34种，故符合条件的选派方案有A39－(A35＋A34)＝420种．8．选B第一步选2女相邻排列C23·A22，第二步另一女生排列A22，第三步男生甲插在中间，1种插法，第四步另一男生插空C14，故有C23·A22·A22·C14＝48种不同排法．9．解析：第一步：将两位爸爸排在两端有2种排法；第二步：将两个小孩视作一人与两位妈妈任意排在中间的三个位置上有A33种排法；第三步：将两个小孩排序有2种排法．故总的排法有2×2×A33＝24(种)．答案：2410．解析：依题意，当甲1人一组时，共有C12C23A22＝12种不同参赛方式；当甲和另1人一组时，共有C13A12A22＝12种不同参赛方式，所以共有24种不同参赛方式．答案：2411．解析：由题意知按选择投资城市的个数分两类：①投资3个城市，每个城市只投资1个项目，有A34种方案；②投资2个城市，其中一个城市投资1个项目，另一个城市投资2个项目．即先从3个项目中选2个看作1个元素(投资在某一个城市)，另一个项目看作1个元素(投资在另一个城市)，然后把这2个元素在4个城市里进行选排，这样有C23A24种方案；所以该公司共有不同的投资方案种数是A34＋C23A24＝60.答案：6012．解析：将7个相同的球放入4个不同的盒子，即把7个球分成4组，因为要求每个盒子都有球，所以每个盒子至少放1个球，不妨将7个球摆成一排，中间形成6个空，只需在这6个空中插入3个隔板将它们隔开，即分成4组，不同的插入方法共有C36＝20种，所以每个盒子都有球的放法共有20种．答案：20第Ⅱ组：重点选做题1．解：(1)分三步完成：第一步，在4个偶数中取3个，有C34种情况；第二步，在5个奇数中取4个，有C45种情况；第三步，3个偶数，4个奇数进行排列，有A77种情况．所以符合题意的七位数有C34C45A77＝100 800个．(2)上述七位数中，3个偶数排在一起的有C34C45A55A33＝14 400个．(3)上述七位数中，3个偶数排在一起，4个奇数也排在一起的有C34C45A33A44A22＝5 760个．2．解：(1)为保证“恰有1个盒不放球”，先从4个盒子中任意取出去一个，问题转化为“4个球，3个盒子，每个盒子都要放入球，共有几种放法？”，即把4个球分成2,1,1的三组，然后再从3个盒子中选1个放2个球，其余2个球放在另外2个盒子内，由分步乘法计数原理，共有C14C24C13×A22＝144种．(2)“恰有1个盒内有2个球”，即另外3个盒子放2个球，每个盒子至多放1个球，也即另外3个盒子中恰有一个空盒，因此，“恰有1个盒内有2个球”与“恰有1个盒不放球”是同一件事，所以共有144种放法．(3)确定2个空盒有C 24种方法，4个球放进2个盒子可分成(3,1)，(2,2)两类，第一类有序不均匀分组有C 34C 11A 22种方法；第二类有序均匀分组有C 24C 22A 22·A 22种方法． 故共有C 24⎝⎛⎭⎫C 34C 11A 22＋C 24C 22A 22·A 22＝84种．。

高二排列与组合反思巩固提高 2015.5一、选择题（每题4分，共48分）：1. 5人站成一排,甲、乙两人之间恰有1人的不同站法的种数 ( )A. 18B. 24C. 36D. 482. 4男5女排成一排，4男顺序一定，5女顺序也一定的排法种数为 （ ） A. 15120 B. 126 C. 3024 D. 以上答案都不对3. 5本不同的书，全部分给四位学生，每个学生至少1本，不同分法的种数是（ ） A ．96 B ．120 C ．240 D ．4804. 在某次数学测验中，学号为)4,3,2,1(=i i 的四位同学的考试成绩}98,96,93,92,90{)(∈i f ，且满足)4()3()2()1(f f f f <≤<，则这四位同学的考试成绩的所有可能情况的种数为（ ）A ．9种B ．5种C ．23种D ．15种5. 从单词“equation ”中选取5个不同的字母排成一排，含有“qu ”（其中“qu ”相连且顺序不变）的不同排法共有（ ）A ．120种B ．480种C ．720种D ．840种6. 从6人中选出4人参加数、理、化、英语比赛，每人只能参加其中一项，每项只能有 一个人去参加，其中甲、乙两人都不能参加英语比赛，则不同的参赛方案的种数共有（ ）种A ．96B ．180C ．240D ．2887. 6个人站成前后两排，每排三人，其中甲不站前排，乙不站在后排的站法种数为（ ） A ．72 B ．216 C ．360 D ．1088. 8个人坐成一排，现要调换其中3个人中每一个人的位置，其余5个人的位置不变，则不同的调换方式有（ ） A ．C 38 B.C 38A 22 C. C 38A 38 D.3C 389. 三人互相传球，由甲开始发球，并作为第一次传球，经过5次传球后，球仍回到甲手 中， 则不同的传球方式共有（ ）A ．6种B ．10种C ．8种D ．16种10. 如果一个三位正整数形如“321a a a ”满足2321a a a a <<且，则称这样的三位数为凸数（如120、363、374等），那么所有凸数个数为（ ）A ．240B ．204C ．729D ．92011. 如图所示，在A 、B 间有四个焊接点，若焊接点接触不好，则可能导致电路不通.今发现A 、B 之间线路 不通，那么焊接点接触不好的不同情况有（ ）． A.13种 B.12 种C.17 种D.15 种12. 某校高三8个班级的师生为庆祝第二十一个教师节，每个班学生准备了一个节目，已排成节目单．开演前又增加了3个教师节目，其中2个独唱节目，1个朗诵节目．如果将这3个节目插入原节目单中，要求教师的节目不排在第一个和最后一个，并且2个独唱节目不连续演出，那么不同的插法有 （ ）A294种 B. 308种 C. 378种 D. 392种请把正确答案填入下面的表格：3二、选择题（每题5分，共20分）：13. 在如图的1×6矩形长条中涂上红、黄、蓝三种颜色，每种颜色限涂两格，且相邻两格不同色，则不同的涂色方案有_____种（用数字作答）．14. 有一排标号为A 、B 、C 、D 、E 、F 的6个座位，请2个家庭共6人入座，要求每个家庭的任何两个人不坐在一起，则不同的入座方法的总数为____ ．（用数字做答）.15. 设坐标平面内有一个质点从原点出发，沿x 轴跳动，每次向正方向或负方向跳1个单位，经过5次跳动质点落在点（3，0）（允许重复过此点）处，则质点不同的运动方法共有______种（用数字作答）.（学以致用：某城镇有东西主要道路四条，南北主要道路六条，现有人从点A 沿主要道路到点B ，有 种不同最近走法.）选择题9.16. ．某校准备召开高中毕业生代表会，把3个班，每班至少一个名额，不同的分配方案共有 种.三、解答题（共52分）： 17. 一个口袋内有4个不同的红球，6个不同的白球，（1）从中任取4个球，红球的个数不比白球少的取法有多少种？（2）若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种？18. 从5名男生，3名女生中选5名担任5门不同学科（含语文，数学）的课代表，求符合下列条件的方法数：（1）女生必须少于男生 （2）女生甲担任语文课代表（3）男生乙必须是课代表，但不任数学课代表（4）女生甲必须担任语文课代表，男生乙必须是课代表，但不任数学课代表19.（1）rr C C -+=1710110则r 可能的值的个数为 （2）如果8771n n n C C C =-+，那么n=_______（3）用五种不同的颜色给图中四个区域涂色，如果每一区域涂一种颜色，相邻区域不能同色， 那么不同的涂色方法共有 种. 20. 有4名男生、5名女生，全体排成一行，问下列情形各有多少种不同的排法?(1)甲不在中间也不在两端； (2)甲、乙两人必须排在两端；(3)男、女生分别排在一起; (4)男女相间；(5)甲、乙、丙三人从左到右顺序保持一定AB21.用0～9这10个数字可以组成没有重复数字的（1）末位是2的三位数有多少个？（2）三位偶数有多少个？（3）比523大的三位数有多少个？。

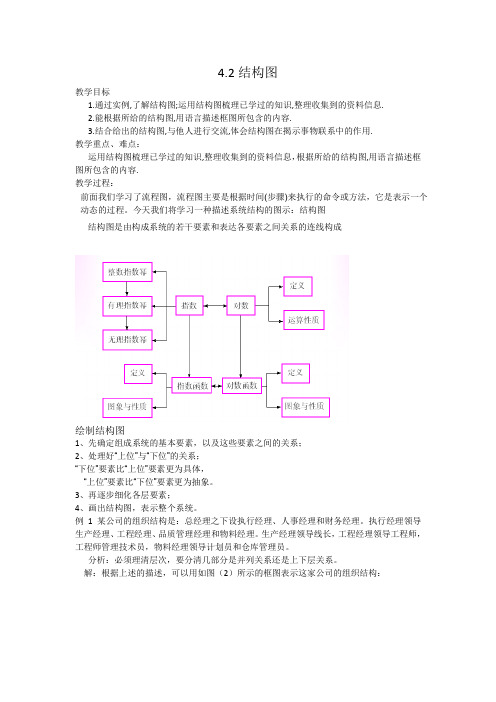
4.2结构图教学目标1.通过实例,了解结构图;运用结构图梳理已学过的知识,整理收集到的资料信息.2.能根据所给的结构图,用语言描述框图所包含的内容.3.结合给出的结构图,与他人进行交流,体会结构图在揭示事物联系中的作用.教学重点、难点：运用结构图梳理已学过的知识,整理收集到的资料信息，根据所给的结构图,用语言描述框图所包含的内容.教学过程：前面我们学习了流程图，流程图主要是根据时间(步骤)来执行的命令或方法，它是表示一个动态的过程。

今天我们将学习一种描述系统结构的图示：结构图结构图是由构成系统的若干要素和表达各要素之间关系的连线构成绘制结构图1、先确定组成系统的基本要素，以及这些要素之间的关系；2、处理好“上位”与“下位”的关系；“下位”要素比“上位”要素更为具体，“上位”要素比“下位”要素更为抽象。

3、再逐步细化各层要素；4、画出结构图，表示整个系统。

例1 某公司的组织结构是：总经理之下设执行经理、人事经理和财务经理。

执行经理领导生产经理、工程经理、品质管理经理和物料经理。

生产经理领导线长，工程经理领导工程师，工程师管理技术员，物料经理领导计划员和仓库管理员。

分析：必须理清层次，要分清几部分是并列关系还是上下层关系。

解：根据上述的描述，可以用如图（2）所示的框图表示这家公司的组织结构：练习：课本90页练习2例2 写出《数学3（必修）》第二章统计的知识结构图。

分析：《数学3（必修）》第二章统计的主要内容是通过对样本的分析对总体作出估计，具体内容又分三部分：“抽样”-------简单随机抽样、系统抽样和分层抽样；“分析”-------可以从样本分布、样本特征数和相关关系这三个角度来分析；“估计”-------根据对样本的分析，推测或预估总体的特征。

解：《数学3（必修）》第二章统计的知识结构图可以用下面图来表示：试画出小流域综合治理开发模式的结构图。

解：根据题意，三类措施为结构图的第一层，每类措施中具体的实现方式为结构为第二层，每类措施实施所要达到的治理功能为结构图的第四层。

2015高中数学 1.2排列与组合学情分析新人教A版选修2-3
学情分析
在学习本节内容前，学生已用了2个课时学习了两个基本计数原理，绝大多数学生能正确运用两个计数原理，但对《排列与组合》这部分内容,不少学生感到难学，其主要原因是:(1)学生对排列组合概念生疏,解题方法也与其他章节不同,具有独特的风格,对学生来说是属于全新的知识；
(2)虽然绝大部分的应用题题意十分简明,但由于排列或组合的种数繁多,往往难以一一列出,使得问题的解决要依赖于抽象思维能力和逻辑推理能力,初学的学生难以适应。

因此，在教学中引导学生遵循先特殊后一般、先取后排、先分类后分步的原则，解决典型的排列问题，借助这些已有的知识，通过类比、归纳，帮助学生理解组合的概念；从能力的角度看，学生已经具备了一定的分析问题的能力、思考的能力、探究的能力、计算的能力、数学表达的能力，教学中要借助学生已有的能力，提供实际问题情境，引导学生进行分析，向学生提供合适的探究材料，引发学生的主动探究，借助小组讨论、全班交流，培养学生的自主学习、合作学习及数学表达能力。

表示
=
2。

《排列与组合》课标分析《排列与组合》作为高中数学的重要内容，不仅在自然科学、社会科学和社会生活中有广泛应用，而且内容本身抽象，逻辑性强，涉及分类、化归、建模等众多数学思想方法，对学生全面发展的培养也具有重要的教育价值，因此，中学阶段学习排列组合,有非常重要的意义。

它是学习二项式定理的重要基础,更是学习概率初步所必需具备的基础知识。

通过学习排列组合可以大大提高学生的抽象思维能力和逻辑推理能力。

人教版高中数学课标教材（A版）将《排列与组合》内容安排在选修2-3第一章，（1）从排列组合内容的《课程标准》来看，教学目标的语言描述上越来越丰富；目标分类上，体现“情感、态度与价值观”领域的目标；目标总量是不断增加的；目标层次的平均要求提高了；（2）从排列组合的课程内容来看，素材选取的数量和内容的丰富程度呈现递增的趋势；（3）从排列组合的课程难度上看，现行教材中排列组合内容的课程难度较大。

（4）从排列组合的编写体例上看，引例插图体现时代精神；框架结构逐渐完整、清晰、逻辑严密。

（5）从排列组合的例题和习题上看，例题和习题总量大体上是增加的趋势，习题类型多样；在习题的综合难度上，习题在“背景”、“探究”、“运算”和“推理”上的难度逐渐提高；在“知识含量”因素上，难度变化不大，一直处于比较平稳的状态。

一、学情调查、情境导入利用自制视频引入新课，根据视频提出问题，引导学生复习旧知，教学中主要以提问为主；利用图片的两个问题，引入新课，让学生自然进入学习状态。

二、问题展示、合作探究1、3个探究问题，层层递进（1）探究1由学生独立思考，总结定义；（2）探究2的教学，学生对比排列数的概念类比得出组合数的定义；（3）探究3学生小组合作讨论积极2、精彩展示（1）探究1，2由学生口头展示；（2）探究3在学生讨论的基础上，由一个小组的学生投影展示；（3）组合数公式的应用例题1，由两名同学板演展示，其中一名同学发现性质1，并在组内同学的帮助下能正确解释性质1；（4）学生投影展示并讲解例题及巩固练习.三、达标检测、巩固提升1、限时6分钟，学生独立完成。