2004年普通高等学校招生全国统一考试(全国1 旧课程)

2004年全国普通高校招生统一考试工作各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢今年的全国普通高校招生统一考试是我市首次自主命题进行的高考，同时，整个高考工作还面临着考生总人数增加、升学比例降低、招生政策进一步调整等实际情况。

我办在区委、区府、区招委、区教委的正确领导下和重庆市招办的指导帮助下，以“三个代表”重要思想为指导思想，认真学习贯彻《教育部关于做好2004年普通高等学校招生工作的通知》及《重庆市2004年普通高等学校招生实施规定》，结合本区实际，进一步强化服务意识，规范管理、与时俱进、开拓创新，圆满地完成了今年的招生考试工作，继续维护了我区招生考试工作服务到位、组织精心、万无一失的良好社会形象，赢得了考生和社会的好评。

现将我区今年的普通高考如下：一、基本情况（一）报名情况今年我区普通高考各类招生考试报名总人数为3043人，比去年2546人增加497人，增幅为%。

其中普通高校考生2347人，比去年1980人增加367人，增幅为%。

三校高职考生人696人，比去年560人增加136人，增幅为%。

实际参加考试高考总人数为2997人，其中文科983人，理科1339人，高职（含中职直升）675人，（二）各类考生上线情况(略)（三）各类考生的录取情况：(略) 二、范文TOP100工作概况（一）领导重视、思想统一我区在重庆市2004年普招工作会召开以后，就及时召开了区招委工作会，我办详细汇报了市普招工作会议精神。

区招委就今年升学形势严峻、命题方式改变、狠抓考风考纪等新情况作了认真研究，提出了统一认识、精心组织、周密部署、严肃考纪、各尽其责、认真办考、万无一失的工作方针，要求我办要进一步深化改革，加强管理，提供优质服务，以“三个代表”重要思想为指导，满腔热情地以高度的政治责任感和历史使命感做好高考工作。

区招委主任、副区长***等领导多次到我办和考点视察招考工作。

5月中旬，区招委召开全体大会，重点研究高考工作，布置任务，落实责任。

2004年普通高等学校招生全国统一考试文科综合能力测试（老课程）本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第I卷注意事项：1．答第I卷前，考生务必将自己姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

3．本卷共35小题，每小题4分，共140分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

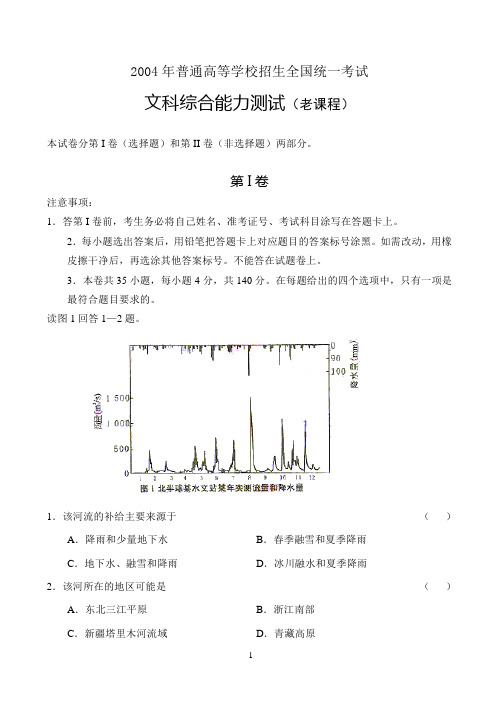
读图1回答1—2题。

1．该河流的补给主要来源于（）A．降雨和少量地下水B．春季融雪和夏季降雨C．地下水、融雪和降雨D．冰川融水和夏季降雨2．该河所在的地区可能是（）A．东北三江平原B．浙江南部C．新疆塔里木河流域D．青藏高原3．下列四幅图中，表示台风过境气压变化的是（）读图2回答4—5题。

4．下列各时段中，气温变化幅度最大的是（）A．1880—1900 B．1920—1940 C．1958—1978 D．1978—19985．全球气候变暖会导致（）A．大气中二氧化碳浓度增加B．全球平均海平面升高，山地永久积雪的下界上升C．全球平均降水量持续增加D．南极地区降水量增加，大陆冰川面积扩大读图3回答6—8题。

6．20世纪下半叶，该国乡村人口的比重（）A．大幅提高B．持续提高C．大幅下降D．持续下降7．该国城市人口比例由30%上升为60%大约用了（）A．30年B．40年C．50年D．70年8．该国位于（）A．亚洲B．欧洲C．北美D．拉丁美洲广西平果县以丰富的铝土资源为基础，发展了氧化铝和电解铝工业，这将会吸引铝电缆、铝铸件和铝连轧等加工企业在此集聚。

回答9—10题9．这些企业在这里集聚的目的是（）A．组建高科技产业基础B．满足当地对铝制品的需求C．减少当地的环境污染D．资源共享和追求集聚效益10．当地电解铝工业发展的能源优势是（）A．火电B．水电C．核电D．风能11．希腊雅典（东2区）19时向世界转播体育比赛实况，我国的体育爱好者在电视中看到该实况的时间是（）A．13时B．次日凌晨1时C．次日17时D．23时城市的发展水平可以反映一个历史时期的社会经济状况。

附：参考答案及解析!""#年普通高等学校招生全国统一考试（全国卷!）$%（理）&本题考查复数的运算%原式’（$(!)($）)’(!)!’!，故选&%（文）&本题考查集合的运算%易知!!"’｛$，*，#｝，则#"!+,’｛$，!，*｝"｛$，*，#｝’｛$，*｝，故选&%!%（理）,本题考查函数的奇偶性%由$（(%）’-.$/%$(%’(-.$(%$/%’($（%），定义域($0%0$，则$（%）为奇函数，由$（&）’’#$（(&）’(’，故选,%（文）,本题考查函数的奇偶性的性质%由$（%）为奇函数，则$（(&）’($（&）’($!，故选,%*%1本题考查向量的运算%由题知2!2’2"2’$，!・"’2!2・2"2・3456"7’$!#2!/*"2!’!!/6!・"/8"!’$!/69$!/89$!’$*#2!/*"$2’$*，故选1%#%,本题考查反函数与原函数之间的关系%由(’%$($/$（%%$）知(%$#%’（(($）!/$，则所求的原函数为(’（%($）!/$，即(’%!(!%/!（%%$），故选,%:%;本题考查二项式定理的有关性质%展开式中的第)/$项为*)/$’1)<（!%*）<()・（($$%）)’1)<・!<()・%!$(*)()!・（($）)，由题可知：!$(*)()!’"得)’6%展开式中常数项为16<・!<(6・（($）6’$#，故选;%6%（理）,本题考查集合之间的运算关系%由已知#&"&+#!+#’!+"，易知,错误，故选,%（文）,本题考查三角函数的求值%由已知可得345!’#:，$!345（!/"#）$’!（345!・345"#(5)=!・5)="#）$’!（#:9$!!(*:9$!!）’$:，故选,%<%1本题考查圆锥曲线的有关问题%将%$’(*代入椭圆方程得(,’$!，由2-.$2/2-.!2’##2-.(!2’#(2-.($2’#($!’<!，故选1%>%1本题考查直线与圆锥曲线的位置关系%由(!’>%#准线%’(!#/（(!，"），设直线的斜率为0（过/与抛物线相交，0一定存在），则直线(’0（%/!）代入(!’>%，得0!（%!/#%/#）’>%#0!%!/（#0!(>）%/#0!’"，当0’"时易知有交点，当0)"时，"%"#（#0!(>）!(#0!・#0!%"，0#(#0!/#(0#%"#0!*$#($*0*$，故选1%8%,本题考查函数图象的平移变换%由(’345!%#(’5)=（"!(!%）#(’5)=［"(（"!(!%）］#(’5)=（!%/"!）#(’5)=!（%/"#），又(’5)=（!%("6）#(’5)=!（%("$!），可见，由(’5)=!（%/"#）向右移动"#/"$!’*"/"$!’"*，得到(’5)=!（%("$!），故选,%$"%;本题考查两个正四面体的棱之间的关系%连结各面中心如图所示，12?"3’$?*，同理可得：四面体1.24的棱与四面体#"53相对应的棱之比均为$?*，则面积之比为其相对棱的比的平方#*?6’$?8，故选;%$$%（理）&本题考查等可能事件发生的概率%能组成满足题中条件的：#）无重复数字有$，*，:；!，*，#，共有;**/;**’$!，$）有重复数字，!，!，:；*，*，*；#，#，$共有;**;!!/$/;**;!!’<，综上共有$!/<’$8，无条件要求有:9:9:’$!:，则满足条件的概率为$8$!:，故选&%（文）1本题考查概率的求法%满足题中条件的为两个奇数一个偶数或三个偶数，则满足题中条件的数为（)）取两个奇数一个偶数：1!:・1$#，（))）取三个偶数有：1*#%总计为1!:1$#/1*#’##%从$，!，…，8中抽*个不同的数有1*8，则满足题中条件的概率为##1*8’$$!$，故选1%$!%,本题考查方程的解法%由题可知&!’$!，’!’$!，7!’*!#&’@$!!，’’@$!!，7’@$6!欲取最小值可得，只有7’($6!，&’’’$!!时（或&’’’($!!，7’$6!）即可，A &’/’7/7&%$!!・$!!/$!!9（($6!）/$!!9（($6!）’$!($*，故选,%$*%（理）｛%2%%($｝本题考查含绝对值不等式的解法%2%/!2%2%2（)）当%%"时，易知%/!%%成立#%%"，（))）当%0"时，2%/!2%(%#%/!%(%或%/!*%#"B %%($，综上可得%%($%（文）｛%2%%"｝本题考查不等式的解法%%（$/%!）%"，C $/%!B "，A %%"，则解集为｛%2%%"｝%$#%%!/(!’#本题考查动点的轨迹方程%由题可知，2(8#2’$，+#-"’6"7#+#-8’*"7，则2(-82’28#25)=*"7’!，设-（%，(），则（%("）!/（(("）$!’!#%!/(!’#%$:%（理）9！!本题考查数列的递推公式的求解%由&9’&$/!&!/*&*/…/（9($）&9($’&$/!&!/…（9(!）&9(!/（9($）&9($’&9($/（9($）&9($（9%*）#&9’9&9($（9%*）#&*&!’*，&#&*’#，…，&9&9($’9#&*&!・&#&*…&9&9($’*9#9…99，故&9’*9#9…99’$9!9*9#9…99!’9！!，当9’!时，&!’&$’$，则&9’$，9’$9！!，9%{!%（文）*・!9(*本题考查等比数列的通项公式的求法%由等比数列的性质&9’&$:9($’&!:9(!’…’&;:9(;#&$"’&*:$"(*#*>#’*9:<#:<’!<#:’!#&9’*・!9(*$6%%&’本题考查直线在平面内的射影的有关问题%两条异面直线在同一平面内的射影不可能出现共线情况，其它都有可能，故有%&’%$<D 本小题主要考查三角函数基本公式和简单的变形，以及三角函数的有关性质%$（%）’（5)=!%/345!%）!(5)=!%345!%!(!5)=%345%’$(5)=!%345!%!（$(5)=%345%）’$!（$/5)=%345%）’$#5)=!%/$!，所以函数$（%）的最小正周期是"，最大值是*#，最小值是$#%$>D （理）本小题主要考查离散型随机变量分布列和数学期望等概念，考查运用概率知识解决实际问题的能力%-（#’"）’"%:!9"%6!’"%"8，-（#’$）’1$!9"%:!9"%6!/1$!9"%:!9"%#9"%6’"%*，-（#’!）’1!!9"%:!9"%6!/1$!1$!9"%:!9"%#9"%6/1!!9"%:!9"%#!’"%*<，-（#’*）’1!!1$!9"%:!9"%#9"%6/1$!1!!9"%:!9"%#!’"%!，-（#’#）’"%:!9"%#!’"%"#，于是得到随机变量#的概率分布列为：#"$!*#-"%"8"%*"%*<"%!"%"#所以1#’"9"%"8/$9"%*/!9"%*</*9"%!/#9"%"#’$%>%（文）本小题主要考查组合、概率等基本概念，独立事件和互斥事件的概率以及运用概率知识解决实际问题的能力%（$）随机选出的*位同学中，至少有一位男同学的概率为$(1*61*$"’:6；（!）甲、乙被选中且能通过测验的概率为答案—$!"#!$"%&’(&$()’"*(+",-（理）本小题主要考查导数的概念和计算，应用导数研究函数性质的方法，考查分类讨论的数学思想+函数!（"）的导数：!.（"）)*"/#"0#"*/#")（*"0#"*）/#"+（1）当#)%时，若"2%，则!.（"）2%，若"3%，则!.（"）3%+所以当#)%时，函数!（"）在区间（45，%）内为减函数，在区间（%，05）内为增函数+（11）当#3%时，由*"0#"*3%，解得"24*#或"3%，由*"0#"*2%，解得4*#2"2%+所以当#3%时，函数!（"）在区间（45，4*#）内为增函数，在区间（4*#，%）内为减函数，在区间（%，05）内为增函数；（111）当#2%时，由*"0#"*3%，解得%2"24*#，由*"0#"*2%，解得"2%或"34*#+所以当#2%时，函数!（"）在区间（45，%）内为减函数，在区间（%，4*#）内为增函数，在区间（4*#，05）内为减函数+（文）本小题主要考查导数的概念和计算，应用导数研究函数单调性的基本方法，考查综合运用数学知识解决问题的能力+求函数!（"）的导数：!.（"）)$#"*06"4"+（1）当!.（"）2%（"!!）时，!（"）是减函数+$#"*06"4"2%（"!!）"#2%且!)$60"*#2%"#24$+所以，当#24$时，由!.（"）2%，知!（"）（"!!）是减函数；（11）当#)4$时，!（"）)4$"$0$"*4"0")4$（"4"$）$0#,，由函数$)"$在!上的单调性，可知当#)4$时，!（"）（"!!）是减函数；（111）当#34$时，在!上存在一个区间，其上有!.（"）3%，所以，当#34$时，函数!（"）（"!!）不是减函数+综上，所求#的取值范围是（45，4$］+*%-本小题主要考查棱锥、二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力+（"）如图，作%&#平面’()*，垂足为点&+连结&(、&’、&*，&(与’*交于点+，连结%++7’*#%(，8’*#&(，7%’)%*，8&’)&*，于是&(平分’*，点+为’*的中点，所以%+#’*+由此知$%+(为面%’*与面’()*所成二面角的平面角，8$%+()"*%9，$%+&)6%9+由已知可求得%+%)$，8%&)%+・%:1;6%9)$&%$*)$*，即点%到平面’()*的距离为$*+（*）解法一：如图建立直角坐标系，其中&为坐标原点，"轴平行于*’+%（%，%，$*），(（%，%$$*，%），%(中点,的坐标为（%，%$$’，$’），连结’,+又知’（"，%$*，%），)（4*，%$$*，%）+由此得到：,’—&)（"，4%$’，4$’），%(—&)（%，%$$*，4$*），()—&)（4*，%，%）+于是有,’—&・%(—&)%，()—&・%(—&)%，所以,’—&#%(—&，()—&#%(—&+,’—&，()—&的夹角"等于所求二面角的平面角，于是<=:"),’—&・()—&>,’—&>>()—&>)4%*??，所以所求二面角的大小为!4@A<<=:%*??+解法二：如图，取%(的中点,，%)的中点-，连结+,、’,、,-，则’,#%(，-,’()，-,)"*()+7’*#%(，8()#%(，-,#%(，8$’,-是所求二面角的平面角+7’*#面%&(，8’*#+,+又7%+)(+，8+,#%(，且$%+,)6%9+在BC (%+,中，+,)%+・<=:6%9)%$*，在BC (,’+中，’+)"*’*)"，于是C@;,’+)+,’+)%$*，又$’,-)!4$,’+，所以所求二面角的大小为!4@A<C@;%$*+*"-本小题主要考查直线和双曲线的概念和性质，平面向量的运算等解析几何的基本思想和综合解题能力+（"）由)与.相交于两个不同的点，故知方程组"*#*4$*)""0${)"，有两个不同的实数解+消去$并整理得（"4#*）"*0*#*"4*#*)%"+所以"4#*)%’#’0##*（"4#*）{3%，解得%2#%2*且#)"+双曲线的离心率/)"0#%*#)"#*%0"，7%2#%2*且#)"，8/3%6*且/)%*，即离心率/的取值范围为（%6*，%*）*（%*，05）+（*）设’（""，$"），(（"*，$*），%（%，"）+7%’—&)("*%(—&，8（""，$"4"）)("*（"*，$*4"）+由此得"")("*"*，由于""，"*都是方程"的根，且"4#*)%，所以"?"*"*)4*#*"4#*，("*"**)4*#*"4#*+消去"*，得4*#*"4#*)*#,6%，由#3%，所以#)"?"$+**-（理）本小题主要考查数列、等比数列的概念和基本知识，考查运算能力以及分析、归纳和推理能力+（"）#*)#"0（4"）")%，#$)#*0$")$，#’)#$0（4"）*)’，#()#’0$*)"$，所以，#$)$，#()"$+（*）#*00")#*00$0)#*04"0（4"）00$0，所以#*00"4#*04")$00（4"）0，同理#*04"4#*04$)$04"0（4"）04"，...，#$4#")$0（4"）+所以（#*00"4#*04"）0（#*04"4#*04$）0 0（#$4#"）)（$00$04"0…0$）0［（4"）00（4"）04"0 0（4"）］，由此得#*00"4#")$*（$04"）0"*［（4"）04"］，于是#*00")$00"*0"*（4"）04"+#*0)#*04"0（4"）0)$0*0"*（4"）04"4"0（4"）0)$0*"*（4"）04"+｛#1｝的通项公式为：当1为奇数时，#1)$10"**0（4"）14"*&"*4"；当1为偶数时，#1)$1**0（4"）1*&"*4"+（文）本小题主要考查等差数列的通项公式、求和公式，考查运算能力+（"）由#1)#"0（14"）2，#"%)$%，#*%)(%，得方程组#"0,2)$%#"0",2{)(%+解得#")"*，2)*+所以#1)*10"%+（*）由31)1#"01（14"）*2，31)*’*得方程"*101（14"）*&*)*’*+解得1)""或1)4**（舍去）+*%%’年普通高等学校招生全国统一考试（全国卷#）"+!本题考查解不等式和集合的运算+易知4：｛">4*2"2*｝，5：｛">4"2"2$｝+4,5)｛">4"2"2*｝，故选!+*-（理）D 本题考查极限的求法+由"*0"4*"*0’"4()（"0*）（"4"）（"0(）（"4"）)答案—*!!"!!#!$%&!"’!"!!("!"!)!(#*$%&!"’!!"!!#*’"，故选+,（文）+本题考查反函数的求法,由"*’!!#（!#(#），"#-!!*’"(#!"*’!(#（!#-），"#(#，故选+,./（理）0本题考查复数的运算,由于’!!*’(’"!$."%*’"!$."%*’)!.)’"($."%*(’(’"!$."%*(’!，故选0,（文）1本题考查导数的几何意义,由题可得"2*.!"(3!，当!*’时，"24!*’*(.，则过（’，(’）处的切线方程为："!’*(.（!(’）!"*(.!!"，故选1,)/0本题考查两曲线关于"*(!对称的之间的关系,#（!，"）*-关于!*("对称的曲线方程为#（("，(!）*-!圆$为：（("(’）"!（(!）"*’!（"!’）"!!"*’，故选0,#/+本题考查三角函数的性质,由题可知：-*567（"8!’"!"）!"!!3*%!（%%!）!"*%!(!3（%%!），故选+,3/9本题考查两图象之间的对称关系,其中"*:!与"*(:!关于!轴对称，"*(:!与"*:(!关于原点对称，故选9,;/1本题考查点到平面距离的求法,由题易知：&&’(*&(’$*&$’&*!"，’’2为’到平面&($的距离，则’4’’24"*’4’&4"!’4’(4"!’4’$4"!4’’24*$..，故选1,</（理）1本题考查数形结合能力,由右图可知：符合条件的直线为"*.，易知，连结&(交"*.于)，则"*.关于直线&(对称的直线)*也满足题中条件，故共有"条，故选1,（文）0本题考查直线与平面所成的角,如下图所示，’为+在底面上的射影，则&+(’即为所求，4’(4*$""，4+(4*’，则在=5’+’(中，>?@+(’*4’(44+(4*$""!&+(’*)#A,B/（理）9本题考查向量的运算,由向量在已知向量上射影定义知：#*4"’&4・>?@C !，"’&$D *#・!・"’&4!4・4"’&4$*#・（()#，.#）・（’，("）’・$#*()#(3#*("，故选9,（文）9本题考查向量的运算,4"(#4*"!（"(#）"*""(""・#!#"*""!""・#*()!""!#"*()!’!)*’!（"!#）"*""!""・#!#"*’"!’!""*3!4"!#$4*3，故选9,’-/（理）1本题考查函数的求导及三角函数的增减性判断,由题知"2*>?@!(!@%7!(>?@!*(!@%7!,故函数"*!>?@!(@%7!的极值点为%!（%*’，"，…）要求函数的增区间，即求"2D -，即!@%7!C -,当!%（!，"!）时，满足!@%7!C -,故选1,（文）1本题考查直线方程的求法,&(的中点为（’!."，"!’"）即（"，."）,&(的垂直平分线的斜率为%*(’(."(’*"!垂直平分线方程为："(."*"（!("）!"*"!(#"!)!(""(#*-，故选1,’’/1本题考查函数的周期性,"*@%7)!!>?@"!*@%7)!(@%7"!!’*(@%7"!（’(@%7"!）!’*(@%7"!>?@"!!’*(’)@%7""!!’*’<（>?@)!(’）!’*’<>?@)!!;<E 周期,*"!)*!"，故选1,’"/0本题考查排列组合的应用,由题可知小于等于".’)#的数有：+))!+..!’，大于等于).#"’的数为：+..!+))!’，则符合条件的数有：+##(（+..!+))!’）(（+..!+))!’）*#<，故选0,’./（理）-,’，-,3，-,.本题考查随机变量的概率分布：都不是红球的概率+（$*-）*0""0"#*-,’，只有一个红球的概率+（$*’）*0’.・0’"0"#*-,3，两个都是红球的概率+（$*"）*0".0"#*-,.，则概率分布为：$-’"+-,’-,3-,.（文）(’"本题考查二项式定理，展开式中的第-!’项为,-!’*0-’-・!’-(-・.-，易知：-*.时，得!;的系数为：0.’-..!0.’-..*(’#!..*(’<!.*(’",’)/#本题考查线性规划问题，!、"满足如右图所示的阴影部分，目标函数/为直线"!!"(/"*-在"轴上截距的一半，由图易知在过（’，’）点时，/最大即/*.8’!"8’*#,’#/!""!""*’本题考查圆锥曲线的基本量之间的关系,由题可知焦点为：（F ’，-），所求椭圆的离心率0*’$"!椭圆中的1.*’$"!.$*"，2"*."(1"*"(’*’，则所求椭圆的方程为!""!""*’,’3/"#本题考查棱柱的定义,$错误，若四棱柱相邻的两个侧面与底面垂直，那么四棱柱为直四棱柱；不相邻的两个侧面与底面垂直，这样的四棱柱不一定是直棱柱，"是真命题，%假命题，#真命题，应填"#,’;/本小题主要考查三角函数概念，两角和、差的三角函数值以及应用、分析和计算能力,（’）证明：G @%7（&!(）*.#，@%7（&((）*’#，E@%7&>?@(!>?@&@%7(*.#@%7&>?@((>?@&@%7(*{’#!@%7&>?@(*"#>?@&@%7(*{’#!567&567(*"，所以567&*"567(,（"）G !"C &!(C !，@%7（&!(）*.#，E 567（&!(）*(.)，即567&!567(’(567&567(*(.),将567&*"567(代入上式并整理得"567"(()567((’*-,解得567(*$"F 3"，舍去负值得567(*$"!3",E 567&*"567($*"!3,设&(边上的高为$3,则&(*&3!3(*$3567&!$3567(*.$3$"!3,由&(*.，得$3$*"!3，所以&(边上的高等于$"!3,’</本小题主要考查组合、概率等基本概念，相互独立事件和互斥事件等概率的计算，运用数学知识解决问题的能力,（’）解法一：三支弱队在同一组的概率为0’#0)<!0’#0)<*’;,故有一组恰有两支弱队的概率为’(’;*3;,解法二：有一组恰有两支弱队的概率0".0"#0)<!0".0"#0)<*3;,（"）解法一：&组中至少有两支弱队的概率0"#0".0)<!0’#0..0)<*’",解法二：&、(两组有一组至少有两支弱队的概率为’，由于对&组和(组来说，至少有两支弱队的概率是相同的，所以&组答案—.中至少有两支弱队的概率为!"#!$%（理）本小题主要考查数列、等比数列的概念和性质，分析和推理能力#证明：（!）&!"’!(#"’!)#"，!"’!("’""#"，*（"’"）#"("（#"’!)#"），整理得"#"’!("（"’!）#"，所以#"’!"’!("#""#故｛#""｝是以"为公比的等比数列#（"）由（!）知#"’!"’!(+・#")!")!（"!"）#于是#"’!(+（"’!）・#")!")!(+!"（"!"）#又!"(,#!(,#故#"(!!’!"(+#因此对于任意正整数"!!，都有#"’!(+!"#（文）本小题主要考查等差、等比数列的概念和性质，考查运算能力#（!）设数列｛!"｝的公差为$，依题意得方程组!!’$($!!’+${("!，解得!!(-，$(+#所以｛!"｝的通项公式为!"(+"’!#（"）由!"(+"’!得%"("+"’!，所以｛%"｝是首项%!("-，公比&("+的等比数列#于是得｛%"｝的前"项和#"("-.（"+")!）"+)!(,".（"+")!）!-#"/%本小题主要考查线面关系和直棱柱等基础知识，同时考查空间想象能力和推理运算能力#解法一：（!）如图，连结’(!、(’!、’)，则’(!"("#&’*(’(!"("，*#’*(!为等腰三角形#又知+为其底边(!*的中点，*’+$(!*#&(!’!(!，’!*!"("，*(!*!"(,#又**!(!，*(!*("#&#(!’*为直角三角形，+为(!*的中点，*’+(!"(!*(!，’+(’’!#又+)(!"(’!("""，+)(’!)#*#’+)%#’’!)#&’+)(&’’!)($/0，即’+$+)#因为(!*、+)为平面*+)内两条相交直线，所以’+$平面*+)#（"）设,、-分别为*’、*+的中点，连结*!-、,-、*!,，则,-’’+，,-(!"’+#*,-(!"，,-$*+#由侧面矩形**!(!(的对角线的交点为+知*+(*!+(!"(!*(!#所以#**!+是边长为!的正三角形，于是*!-$*+，*!-(","#*&*!-,是所求二面角的平面角#又*!,"(*!*"’*,"(!’（"""）"(,"，*123*!-,(*!-"’,-")*!,""*!-・,-(（","）"’（!"）"),""・","・!"()",,#即所求二面角的大小为!)451123",,#解法二：如图，以’为原点建立坐标系#（!）*（""，/，/），*!（""，!，/），(!（/，!，!），+（"""，!"，!"），)（"""，!，/），’+—((（"""，!"，!"），(!*—((（""，)!，)!）#+)—((（/，!"，)!"），则’+—(・(!*—((/，’+—(・+)—((/，*’+$(!*，’+$+)，因为(!*、+)为平面*+)内两条相交直线，所以’+$平面*+)#（"）设*+中点为-，连结*!-，则-（","+，!+，!+），*+—((（)"""，!"，!"），*!-—((（)""+，),+，!+），**+—(・*!-—((/，**+$*!-#又’+$*+，*’+—(与*!-—(的夹角!等于所求二面角的平面角#123!(’+—(・*!-—(6’+—(66*!-—(6()",,#所以所求二面角的大小为!)451123",,#"!%本小题主要考查抛物线的性质，直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力#（!）’的焦点为,（!，/），直线.的斜率为!，所以.的方程为/(0)!#将/(0)!代入方程/"(+0，并整理得0")70’!(/#设(（0!，/!），*（0"，/"），则有0!’0"(7，0!0"(!#1(—(・1*—((（0!，/!）・（0"，/"）(0!0"’/!/"("0!0")（0!’0"）’!(),#61(—(661*—(6(0"!’/""!・0""’/"""(0!0"［0!0"’+（0!’0"）’!7"］"(+!#123〈1(—(，1*—(〉(1(—(・1*—(61(—(661*—(6()",+!+!，所以1(—(与1*—(夹角的大小为!)451123",+!+!#（"）由题设,*—(("(,—(得（0")!，/"）("（!)0!，)/!），即0")!("（!)0!）"/"()"/!{#，由#得/""(""/"!#&/"!(+0!，/""(+0"，*0"(""0!$，联立"、$解得0"("，依题意有"8/#**（"，"""），或*（"，)"""），又,（!，/），得直线.方程为（")!）/("""（0)!）或（")!）/()"""（0)!）#当")［+，$］时，.在/轴上的截距为"""")!或)"""")!#由"""")!("""’!’"")!，可知"""")!在［+，$］上是递减的，*,+*"""")!*+,，)+,*)"""")!*),+#直线.在/轴上截距的变化范围为［)+,，),+］+［,+，+,］#""%（理）本小题主要考查导数的基本性质和应用、对数函数性质和平均值不等式等知识以及综合推理论证的能力#（!）函数2（0）的定义域为（)!，’9）#2:（0）(!!’0)!#令2:（0）(/，解得0(/#当)!;0;/时，2:（0）8/，当08/时，2:（0）;/#又2（/）(/，故当且仅当0(/时，2（0）取得最大值，最大值为/#（"）证法一：3（!）’3（%）)"3（!’%"）(!<=!’%<=%)（!’%）<=!’%"(!<="!!’%’%<="%!’%#由（!）结论知<=（!’0）)0;/（08)!，且0,/），由题设/;!;%，得%)!"!8/，)!;!)%"%;/，因此<="!!’%()<=（!’%)!"!）8)%)!"!，<="%!’%()<=（!’!)%"%）8)!)%"%#所以!<="!!’%’%<="%!’%8)%)!")!)%"(/#又"!!’%;!’%"%#!<="!!’%’%<="%!’%;!<=!’%"%’%<="%!’%(（%)!）<="%!’%;（%)!）<="#综上，/;3（!）’3（%）)"3（!’%"）;（%)!）<="#证法二：3（0）(0<=0，3:（0）(<=0’!#设,（0）(3（!）’3（0）)"3（!’0"），则,:（0）(3:（0）)"［3（!’0"）］:(<=0)<=!’0"#当/;0;!时，,:（0）;/，因此,（0）在（/，!）内为减函数#当08!时，,:（0）8/，因此,（0）在（!，’9）上为增函数#从而，当0(!时，,（0）有极小值,（!）#因此,（!）(/，%8!，所以,（%）8/，即/;3（!）’3（%）)"3（!’%"）#设-（0）(,（0）)（0)!）<="，则-（0）(<=0)<=!’0")<="(<=0)<=（!’0）#当08/时，-:（0）;/#因此-（0）在（/，’9）上为答案—+减函数!因为!（"）"#，#$"，所以!（#）%#!即$（"）&$（#）’($（"&#(）%（#’"）)*(!（文）本小题主要考查导数的概念和计算，应用导数研究函数单调性的基本方法，考查综合运用数学知识解决问题的能力!函数%（&）的导数%+（&）"&(’"&&"’,，令%+（&）"#，解得&",或&""’,!当"’,!,即"!(时，函数%（&）在（,，&-）上为增函数，不合题意!当"’,$,即"$(时，函数%（&）在（’-，,］上为增函数，在（,，"’,］内为减函数，在（"’,，&-）上为增函数!依题意应有，当&"（,，.）时，%+（&）%#，当&"（/，&-）时，%+（&）$#!所以.!"’,!/，解得0!"!1，所以"的取值范围是［0，1］!(##.年普通高等学校招生全国统一考试（全国卷!）,2（理）3本题考查集合的运算!由题知’"｛#，(，.｝#($’"｛#，,，(｝$｛#，(，.｝"｛#，(｝，故选3!（文）4本题考查集合的运算!%)’"｛#，(，5｝#($（%)’）"｛#，5，0｝$｛#，(，5｝"｛#，5｝，故选4!(26本题考查反函数的求法!由*"7(&$##(&")**#&",()**#*",()*&（&$#），故选6!52（理）8本题考查两直线的位置关系!与&’(*&5"#垂直的直线的斜率+"’(，则过点（’,，5）的直线方程为：*’5"’(（&&,）#*&(&’,"#，故选8!（文）3本题考查求圆的方程，设圆心为（"，#），且"$#，则（"，#）到直线5&&.*&."#的距离为(，即95:"&.:#&.95(&.&("(#5"&.";,##""(或""’,.5（舍去），则圆的方程为：（&’(）(&（*’#）("((即&(&*(’.&"#，故选3!.!（理）3本题考查复数的运算!原式"（&,’5<,&<）("&,’(5<’5(<&"’5&<，故选3!（文）3本题考查导数的求法!易知*+"(（&&,）（&’,）&（&&,）("(&(’(&&(&(&&,"5&(&(&’,，在&",处的导数为：5:,(&(:,’,".，故选3!02（理）8本题考查不等式的解法!原不等式等价于（&&(）&（&’5）%#，令（&&(）&（&’5）"#得&,"’(，&("#，&5"5，将数轴分成四部分，可见，不等式的解集为：｛&9#%&%5或&%’(｝，故选8!（文）3本题考查函数图象的平移!*"5:（,5）&"（,5）&’,，则只需把*"（,5）&的图象向右平移,个单位，故选3!/24本题考查等差数列的性质，由已知可得（",&"(&"5）&（",=&",>&"(#）"’(.&1=#（",&"(#）&（"(&",>）&（"5&",=）"0.#",&"(#",=#,(#"",&"(#(:(#",=(:(#",=#，故选4!12（理）6本题考查简单多面体中线面位置关系的判定!8中-与!关系不确定，4同8，6为真命题，3中.与-也可能相交，故选6!（文）8本题考查几何体的体积!由题易知正三棱柱的侧面为正方形并且底面边长为&(，则三棱柱的体积为：&5.（&(）(&:("&/(，故选8!=2（理）8本题考查圆锥曲线的基本性质，亦知抛物线的焦点为（’,，#），则椭圆/",，由/"",(得""(##""(’/&(&"5#标准方程为&(.&*(5",，故选8!（文）6本题考查诱导公式和三角函数的求值!原式"(?@A（"/&&）’?@A （"/&&）"?@A （"/&&）’’,，故选6!>24本题考查排列组合的应用!（#）全为女班主任有：85.，（$）全为男班主任有：850，5位班主任中男女都有为：85>’85.’850"0#.’(.’/#".(#种，应选4!,#2（理）8本题考查球的有关性质，由题可知球的半径0满足."0("(#"#0&"0!由题易知(123",(#B ，如下图，4为球心，2、1、3为球面上的点，44+)面213于4+，易知4+2为(123的平分线，C (124+"/#B ，C *214+为正三角形，则在*244+中44+的长度为42(’4+2&("（&0）(’(&(",，故选8!（文）2本题考查球的有关性质，由题易知球的半径0满足."0("(#"#0&"0!如图，4为球心，44+)面213于4+，因*213为等边三角形，4+必为*213的中心，则在DE *244+中，4+2"&5521"(，所以44+"24(’4+2&("（&0）(’(&(",，故选82,,!4本题考查解三角形!由"、#、/成等差数列则"&/"(##"(&("/&/(".#(，由余弦定理可得#(""(&/(’("/・?@A 1，,("/A<*1"5(#("/",(，综合以上三式可得#(&,(・?@A 5#B &,(".#(##(&"(5&."（&5&,）(##&"5&,，故选4!,(2（理）6本题考查函数的性质!由题可知%（,）"%（’,&(）"%（’,）&%（(）"’%（,）&%（(）#%（,）"’%（,）&%（(）#%（(）"(%（,）"(:,(",，则%（&&(）"%（&）&,#%（0）"%（5&(）"%（5）&,"%（,&(）&,"%（,）&("(，故选6!（文）8本题考查直线与对数函数间的关系，由于2点在*")@F ,.&的图象上，则2点满足*")@F ,.("’,(#2（(，’,(），又2在*"+&上#’,("+:(#+"’,.，故选8!,52(=本题考查二项式定理!则（&’,&&）=的第5&,项为65&,"65=・&=’5・&’5(（’,）5"65=（’,）5・&=’5(5，当=’5(5"0时，得5"(，则&0系数为6(=（’,）("1:=("(=!,.2’,(本题考查向量的数量积的应用!由（!’"）（(!&"）"’.#(!(’!・"’"("’.，又9!9"(，9"9".#’!・""’.&.(’(:((".，由?@A 〈!，"〉"!・"9!9・9"9"’.(:."’,(!,02（理）5.本题考查三角函数的最值求法!%（&）"?@A &’,(?@A (&"?@A &’,(（(?@A (&’,）"’?@A (&&?@A &&,("’（?@A &’,(）(&5.!5.!（文）5(本题考查正弦函数的周期性!*",(A<*&&"2",(A<*（,2&&"2），其最小正周期为(",2"(2""5"，所以2"5(!,/2(本题考查线性规划方面的问题!&、*满足的约束条件，如右图阴影部分，目标函数7"(&&*表示直线(&&*’7"#在*轴上的截距，可见当直线过（,，#）时截距最大#7"(:,&#"(!,12本小题主要考查同角三角函数的基本关系式，二倍角公式以及三角函数式的恒等变形等基础知识和基本技能!A<*（!&".）A<*(!&?@A (!&,"&((（A<*!&?@A !）(A<*!?@A !&(?@A (!"&(（A<*!&?@A !）.?@A !（A<*!&?@A !）!当!为第二象限角，且A<*!"&,0.时，答案—0!"#!$%&!!!’，%&!!()*+，所以!"#（!$!+）!"#,!$%&!,!$*(",+%&!!"(),-*./（理）本小题主要考查函数的导数计算，利用导数讨论函数的性质，判断函数的最大值、最小值以及综合运算能力-!0（"）(**$")*,"，令**$")*,"(’，化简为",$"),(’，解得"*(),（舍去），",(*-当’#"1*时，!0（"）2’，!（"）单调增加；当*1"#,时，!0（"）1’，!（"）单调减小；所以!（*）(3#,)*+为函数!（"）的极大值-又因为!（’）(’，!（,）(3#4)*2’，!（*）2!（,），所以!（’）(’为函数!（"）在［’，,］上的最小值，!（*）(3#,)*+为函数!（"）在［’，,］上的最大值-（文）本小题主要考查导数的几何意义，两条直线垂直的性质以及分析问题和综合运算能力-（*）#0(,"$*-直线$*的方程为#(4")4-设直线$,过曲线#(",$"),上的点%（&，&,$&),），则$,的方程为#(（,&$*）")&,),-因为$*$$,，则有,&$*()*4，&(),4-所以直线$,的方程为#()*4"),,5-（,）解方程组#(4")4#()*4"),,{5得"(*6#(){7,-所以直线$*和$,的交点的坐标为（*6，)7,）-$*、$,与"轴交点的坐标分别为（*，’）、（),,4，’）-所以所求三角形的面积’(*,8,7489)7,9(*,7*,-*5/（理）本小题主要考查离散型随机变量的分布列、数学期望等概念，以及运用概率统计知识解决实际问题的能力-（*）"的可能取值为)4’’，)*’’，*’’，4’’-(（"()4’’）(’-,4(’-’’.，(（"()*’’）(48’-,,8’-.(’-’56，(（"(*’’）(48’-,8’-.,(’-4.+，(（"(4’’）(’-.4(’-7*,，所以"的概率分布")4’’)*’’*’’4’’(’-’’.’-’56’-4.+’-7*,根据"的概率分布，可得"的期望)"(（)4’’）8’-’’.$（)*’’）8’-’56$*’’8’-4.+$4’’8’-7*,(*.’-（,）这名同学总得分不为负的概率为(（"%’）(’-4.+$’-7*,(’-.56-（文）本小题主要考查相互独立事件同时发生的概率和互斥事件有一个发生的概率的计算方法，应用概率知识解决实际问题的能力-记“这名同学答对第*个问题”为事件+*（*(*，,，4），则(（+*）(’-.，(（+,）(’-:，(（+4）(’-6-（*）这名同学得4’’分的概率(*((（+*+,—+4）$(（+*—+,+4）((（+*）(（+,—）(（+4）$(（+*—）(（+,）(（+4）(’-.8’-48’-6$’-,8’-:8’-6(’-,,.-（,）这名同学至少得4’’分的概率(,((*$(（+*+,+4）(’-,,.$(（+*）(（+,）(（+4）(’-,,.$’-.8’-:8’-6(’-76+-,’/本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析问题能力-（*）如图，取+,的中点)，连结()，则()$+,-作(-$平面+%./,，垂足为-，连结-)-根据三垂线定理的逆定理得-)$+,，所以&()-为侧面(+,与底面所成二面角的平面角-由已知条件可知&()-(6’;，()(6，所以(-"(44，四棱锥(—+%/,的体积0(—+%/,(*4""8.8+4844(56-（,）解法一：如上图以-为原点建立空间直角坐标系-通过计算可得(（’，’，"44），+（",4，)4，’），%（",4，7，’），,（"),4，)4，’），所以(+—’(（",4，)4，")44），%,—’(（")+4，).，’），因为(+—’・%,—’(),+$,+$’(’，所以(+$%,-解法二：如图所示，连结+-，延长+-交%,于点1-通过计算可得)-(4，+)"(,4，又知+,("+4，+%(.，得)-+)(+,+%-所以<=(+)-)<=(%+,-得&)+-(&+%,-得&)+-$&+,1(5’;，所以+1$%,-因为直线+1为直线(+在平面+%/,内的射影，所以(+$%,-,*/本小题主要考查点到直线距离公式，双曲线的基本性质以及综合运算能力-直线$的方程为"2$#&(*，即&"$2#)2&(’-由点到直线的距离公式，且22*，得到点（*，’）到直线$的距离3*(&（2)*）2,$&",，同理得到点（)*，’）到直线$的距离3,(&（2$*）2,$&",，4(3*$3,(,2&2,$&",(,2&5-由4%+75，得,2&5%+75，即725,)2",%,5,-于是得76,")*%,6,，即+6+),76,$,7#’-解不等式，得7+#6,#7-由于62*2’，所以6的取值范围是"7,#6#"7-,,/（理）本小题主要考查函数的导数，三角函数的性质，等差数列与等比数列的概念和性质，以及综合运用的能力-（*）!0（"）()>)"（%&!"$!"#"）$>)"（)!"#"$%&!"）(),>)"!"#"-由!0（"）(’，得),>)"!"#"(’-解出"(7!，7为整数-从而"7(7!，7(*，,，4，…，!（"7）(（)*）7>)7!，!（"7$*）!（"7）()>)!-所以数列｛!（"7）｝是公比8()>)!的等比数列，且首项!（"*）(8-（,）’7("*!（"*）$",!（",）$…$"7!（"7）(!8（*$,8$…$787)*），8’7(!8（8$,8,$…$787），’7)8’7(!8（*$8$…$87)*)787）(!8（*)87*)8)787），从而’7(!8*)8（*)87*)8)787）-’*$’,$…$’77(!8（*)8）,)!8,7（*)8）4（*$8$…$87)*）)!8,7（*)8）（*$,8$…$787)*）(!8（*)8）,)!8,7（*)8）,*)87*)8)!8,7（*)8）,（*)87*)8)787）(!8（*)8）,),!8,7（*)8）4（*)87）$!87$,（*)8）,-因为989(>)!1*，3"?7’@87(’，所以3"?7’@’*$’,$…$’77(!8（*)8）,()!>!（>!$*）,-（文）本小题主要考查等比数列的概念，前7项和公式等基础知识，考查学生综合运用基础知识进行运算的能力-（*）设等比数列｛27｝的公比为8，则2,(2*8，27(2*8+-依题意，得方程组2*8(62*8+{(*6,-解此方程组，得2*(,，8(4-故数列｛27｝的通项公式为27(,・47)*-（,）’7(,（*)47）*)4(47)*，’7・’7$,’,7$*(4,7$,)（47$47$,）$*4,7$,),・47$*$*#4,7$,),47・47"$,$*4,7$,),・47$*$*(*，即’7・’7$,’,7$*#*-,’’+年普通高等学校招生全国统一考试（全国卷"）*-A 本题考查集合的运算-9表示单位圆上的点的集合-:表示抛物线上的点的集合-9*:表示圆与抛物线交点的个数，即为",$#,(*",)#{(’解的个数，消去"得#,$#)*(’，#2’，有两个解一个正、一个负，又#%’，则负根舍去-代入原方程"有两个，则方程组有两组解，故对应两个交点，则应选A-另解：数形结合，抛物线顶点（’，’）在圆内部，则抛物线与圆有两个交点，故选A-答案—6!"#本题考查三角函数的周期"!（"）$%&’("!%!!（!!)"）$%&’(!!)"!%$%&’(（!)"!）%$%*&’("!%$%&’("!%，!（!)"）$%&’(!)"!%$%&’(（!!)"!）%$%+,&"!%"!（"），则最小正周期为!!，另解数形结合求解"-"（理）.本题考查数列的性质"由题可知，数列的公差#$$/*$!/*!$0*（*0）0$!，然后根据前%项和公式求出&1、&2、&0，可得."另解：由$!)$/$3!$2$3，则前1项和与前2项和相等，故选."（文）.本题考查等比数列的前%项和公式，设公比为’则’-$$2$!$!1-4$!5!’$-，则前1项的和为：-)4)!5)/6$6!3，故选."1"7本题考查圆的切线的有关问题"易知圆心(（!，3），则()连线的斜率为*+,$#-*36*!#$*-!切)点的切线斜率*$*6*+,$6#-!过)点切线方程-#*-$6#-（"*6）!"*#--)!$3，故选7"2"（理）8本题考查函数的定义域"由题易知39"!*6$6!69"!$!!#*!$"9*6或69"$#!，故选8"（文）.本题考查原函数与反函数之间的关系"设.（63）$$!!（$）$63!6)-*$$63!-*$$-!!$$*!，故选."0"8本题考查复数的三角形式"设其三角形式为：/$0（+,&!-!)’&’(!-!）$*6!0)#-!0’，由题知：#-!0#$-!0$!，则/#$*6)-’!/!#$*!*!-’，故选8"5"#本题考查双曲线的性质"由题可知1$$6!!$$!1，又+!$$!)1!$$!)$!1$21$!!+$$#2!，故选#"/"7本题考查绝对值不等式的解法"原不等式等价于")6%369"{)69-或")693*-9"{)69*6!"%*639"{9!或"9*6*19"{9*!!39"9!或*19"9*!，故选7"4"#本题考查几何体体积的求法，易知正三棱锥的侧棱长为#!，则其体积为60（#!）-$#!-，故选#"（若一个三棱锥的三条侧棱两两相互垂直且侧棱长分别为$、1、+，则其体积为6$1+）63".本题考查三角形的解法"由余弦定理可得：+,&2$2(!)23!*3(!!2(・23$1!)-!*（#6-）!!:-:1$6!";&’(2$#-!，则2(边上的高4$23・&’(2$-:#-!$-!#-，故选."66"（理）8本题考查不等式的解法"使得!（"）%6成立，有"96（")6）!%{6或"%61*"#*6%{6!"96%")6%%{6或"%6"#*6${-!"96")6%6或")6${*6或"%63$"*6${4!3$"96或"$*!或6$"$63!"$*!或3$"$63，故选8"（文）8本题考查二项式定理"由题可知展开式中第0)6项为：50)6$#00・（#"）0*0・（*6"）0$#00・"-*0!・（*6）0・"*0$（*6）0・#00"-*-!0，当0$!时，即第-项为常数项，其值为：（*6）!・#!0$0:2!$62，故选8"6!"#本题考查排列组合的应用"首先将四名老师进行分成-组有#!1，然后将其进行全排列有8--，由乘法原理有#!18--$-0"6-"-60本题考查球的性质"由题易知，如右图截面半径0为：0$6!*（6!）#!$#-!6，截面的面积&截$!0!$!:（#-!6）!$-1!6!"球的表面积为&球$1!6!，则：&截<&球$-1!6!<1!6!$-<60$-60"61"（理）6本题考查三角函数的最值"则-$&’("#)-+,&"$!（6!&’(")#-!+,&"）$!・&’(（")!-），由"&［3，!!］，;!-$")!-$2!0，;-%!&’(!0$6"（文）#2!本题考查三角函数的最值"由题可知，-$#2!&’(（")!）（其中!$=>+?=(（*!）），其最大值为#2!"62"（理）*!本题考查函数的性质"设"93，则*"@3，!（*"）$-*"*6"又!（*"）$*!（"）!!（"）$*-*")6，A !（"）与.（"）互为反函数!设.（*/）$$!!（$）$*/，又当"%3时，!（"）%3，当"93，!（"）93!*-*$)6$*/!-*$$-!!$$*!"（文）｛"%69"$!｝本题考查函数的定义域"由题可知39"*6$6!69"$!"60"（理）#2本题考查抛物线的性质"由定义可知，)点到-轴的距离等于)点到7（!，3）的距离，即)点到2点与到-轴的距离之和等于%)2%)%)7%，又%)2%)%)7%%%27%，即2、)、7三点共线时最小，即最小值为%27%$（!*3）!)（3*6）#!#$2"（文）6本题考查数形结合能力"由下（右）图可知，设圆心到直线的距离为#!#$%3*3*63%-!)1#!$!@6，则圆上的点到直线的最小值为：!*6$6"（理）（文）65B 本小题主要考查同角三角函数的基本关系、二倍角公式等基础知识以及三角恒等变形的能力"原式$&’("+,&!"!&’("+,&"+,&!"，因为?=("$6!时，&’(""3，+,&!""3，所以原式$6!+,&""因为"为锐角，由?=("$6!得+,&"$!#2，;原式$#21"6/B（理）本小题主要考查解带绝对值的方程以及指数和对数的概念与运算"当6*!"%3，即"$3时，原方程化为1"*!")6$66，（!"*6!）!$161，解得!"$6!C #16!"!"$6!*#16!93，无解"由!"$6!)#16!@6知"@3，舍去"当6*!"93，即"@3时，原方程化为1")!"*6$66，（!")6!）!$141，解得!"$*6!C5!，!"$*6!*5!93，无解"!"$*6!)5!，"$D,E !-@3"原方程的解为"$D,E !-"（文）本小题主要考查指数和对数的性质以及解方程的有关知识"（!"）!*1（!"）*6!$3"（!"*0）（!")!）$3"故!"$0，!"$*!（无解）"所以"$D,E !0"64B本小题主要考查把实际问题抽象为数学问题，应用不等式等基础知识和方法解决问题的能力"设矩形温室的左侧边长为$F ，后侧边长为1F ，则$1$/33"蔬菜的种植面积&$（$*1）（1*!）$$1*11*!$)/$/3/*!（$!)!1）"所以&$/3/*1!#$1$01/（F !）"当$$!1，即$$13（F ），1$!3（F ）时，&最大值$01/（F !）"答：当矩形温室的左侧边长为13F ，后侧边长为!3F 时，蔬菜的种植面积最大，最大种植面积为01/F !"!3B 本小题主要考查两个平面垂直的性质，直线与平面所成角等有关知识，以及逻辑思维能力和空间想象能力"（6）如图6，取2(中点8，连结)8、38"因为)2$)(，所以)8’2(，又已知面)2(’面23(，所以)8’面23(，8为垂足"答案—5。

2004年普通高等学校招生全国统一考试数学（理工类）（上海卷）一、填空题(本大题满分48分,每小题4分) （1）若tgα=21,则tg(α+4π)= . （2）设抛物线的顶点坐标为(2,0),准线方程为x=－1,则它的焦点坐标为 . （3）设集合A={5,log 2(a +3)},集合B={a ,b}.若A∩B={2},则A ∪B= . （4）设等比数列{a n }(n ∈N)的公比q=－21,且∞→n lim (a 1+a 3+a 5+…+a 2n-1)=38,则a 1= .（5）设奇函数f(x)的定义域为[－5,5].若当x ∈[0,5]时, f(x)的图象如右图,则不等式f(x)<0的解是 .（6）已知点A(1, －2),若向量与a ={2,3}同向,=213,则点B 的坐标为 .（7）在极坐标系中,点M(4,3π)到直线l :ρ(2cosθ+sinθ)=4的距离d= . （8）圆心在直线2x －y －7=0上的圆C 与y 轴交于两点A(0, －4),B(0, －2),则圆C 的方程为 .（9）若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 . (结果用分数表示)（10）若函数f(x)=a 2+-b x 在[0,+∞]上为增函数,则实数a 、b 的取值范围是 .（11）教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是.（12）若干个能唯一确定一个数列的量称为该数列的“基本量”.设{a n }是公比为q 的无穷等比数列,下列{a n }的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号)①S 1与S 2; ②a 2与S 3; ③a 1与a n ; ④q 与a n . 其中n 为大于1的整数, S n 为{a n }的前n 项和.二、选择题(本大题满分16分,每小题4分)（13）在下列关于直线l 、m 与平面α、β的命题中,真命题是（A ）若l ⊂β且α⊥β,则l ⊥α. （B ）若l ⊥β且α∥β,则l ⊥α.（C ）若l ⊥β且α⊥β,则l ∥α.（D ）若α∩β=m 且l ∥m,则l ∥α. （14）三角方程2sin(2π－x )=1的解集为（A ）{x │x =2kπ+3π,k ∈Z}.（B ）{x │x =2kπ+35π,k ∈Z}.（C ）{x │x =2kπ±3π,k ∈Z}.（D ）{x │x =kπ+(－1)K ,k ∈Z}.（15）若函数y=f(x)的图象可由函数y=lg(x +1)的图象绕坐标原点O 逆时针旋转2π得到,则f(x)=（A ）10－x －1.（B ）10x －1. （C ）1－10－x .（D ）1－10x .（16）某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是（A ）计算机行业好于化工行业. （B ）建筑行业好于物流行业.（C ）机械行业最紧张.（D ）营销行业比贸易行业紧张.三、解答题(本大题满分86分) （17）(本题满分12分)已知复数z 1满足(1+i )z 1=－1+5i , z 2=a －2－i , 其中i 为虚数单位,a ∈R, 若21z z -<1z ,求a 的取值范围.（18）(本题满分12分)某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位：m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少(精确到0.001m) 时用料最省?记函数f(x)=132++-x x 的定义域为A, g(x )=lg[(x －a －1)(2a －x )](a <1) 的定义域为B. （Ⅰ）求A ；（Ⅱ）若B ⊆A, 求实数a 的取值范围.已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).（Ⅰ）求函数f(x)的表达式；（Ⅱ）证明:当a>3时,关于x的方程f(x)= fA有三个实数解.如图，P —ABC 是底面边长为1的正三棱锥,D 、E 、F 分别为棱长PA 、PB 、PC 上的点, 截面DEF ∥底面ABC, 且棱台DEF —ABC 与棱锥P —ABC 的棱长和相等.(棱长和是指多面体中所有棱的长度之和)（Ⅰ）证明：P —ABC 为正四面体； （Ⅱ）若PD=21PA, 求二面角D —BC —A 的大小；(结果用反三角函数值表示) （Ⅲ）设棱台DEF —ABC 的体积为V , 是否存在体积为V 且各棱长均相等的直平行六面体,使得它与棱台DEF —ABC 有相同的棱长和? 若存在,请具体构造出这样的一个直平行六面体,并给出证明；若不存在,请说明理由.设P 1(x 1,y 1), P 1(x 2,y 2),…, P n (x n ,y n )(n≥3,n ∈N) 是二次曲线C 上的点, 且a 1=1OP 2, a 2=2OP 2, …, a n =n OP 2构成了一个公差为d(d≠0) 的等差数列, 其中O 是坐标原点. 记S n =a 1+a 2+…+a n .（Ⅰ）C 的方程为2510022y x +=1,n=3. 点P 1(3,0) 及S 3=255, 求点P 3的坐标； (只需写出一个)（Ⅱ）若C 的方程为12222=+by a x (a >b>0). 点P 1(a ,0), 对于给定的自然数n, 当公差d变化时, 求S n 的最小值；（Ⅲ）请选定一条除椭圆外的二次曲线C 及C 上的一点P 1,对于给定的自然数n,写出符合条件的点P 1, P 2,…P n 存在的充要条件,并说明理由.2004年普通高等学校招生全国统一考试 数学参考答案（理工类）（上海卷）一、填空题(本大题满分48分,每小题4分)（1）3 （2）(5,0) （3）{1,2,5} （4）2 （5）(－2,0)∪(2,5] （6）(5,4) （7）5152 （8）(x －2)2+(y+3)2=5 （9）114（10）a >0且b≤0 （11）用代数的方法研究图形的几何性质 （12）①、④二、选择题(本大题满分16分,每小题4分)（13）B （14）C （15）A （16）B 三、解答题(本大题满分86分) （17）【解】由题意得 z 1=ii++-151=2+3i , 于是21z z -=i a 24+-=4)4(2+-a ,1z =13.4)4(2+-a <13,得a 2－8a+7<0,1<a<7.（18）【解】由题意得 x y+41x 2=8,∴y=x x 482-=48x x -(0<x <42). 于定, 框架用料长度为 l=2x +2y+2(x 22)=(23+2)x +x 16≥4246+.当(23+2)x=x16,即x=8－42时等号成立. 此时, x≈2.343,y=22≈2.828.故当x 为2.343m,y 为2.828m 时, 用料最省. （19）【解】(1)2－13++x x ≥0, 得11+-x x ≥0, x <－1或x ≥1 即A=(－∞,－1)∪[1,+ ∞](2) 由(x －a －1)(2a －x )>0, 得(x －a －1)(x －2a)<0.∵a <1,∴a +1>2a , ∴B=(2a ,a +1). ∵B ⊆A, ∴2a ≥1或a +1≤－1, 即a ≥21或a ≤－2, 而a <1, ∴21≤a <1或a ≤－2, 故当B ⊆A 时, 实数a 的取值范围是(－∞,－2]∪[21,1) （20）【解】(1)由已知,设f 1(x)=ax 2,由f 1(1)=1,得a =1, ∴f 1(x)= x 2. 设f 2(x)=xk(k>0),它的图象与直线y=x 的交点分别为A(k ,k )B(－k ,－k )由AB =8,得k=8,. ∴f 2(x )=x 8.故f(x)=x 2+x8. (2) 【证法一】f(x)=fA ,得x 2+x 8=a 2+a8,即x 8=－x 2+a 2+a8.在同一坐标系内作出f 2(x)=x8和f 3(x)= －x 2+a 2+a8的大致图象,其中f 2(x)的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线, f 3(x)与的图象是以(0, a 2+a8)为顶点,开口向下的抛物线.因此, f 2(x)与f 3(x)的图象在第三象限有一个交点, 即f(x)=fA 有一个负数解. 又∵f 2(2)=4, f 3(2)= －4+a 2+a8 当a >3时,. f 3(2)－f 2(2)= a 2+a8－8>0, ∴当a >3时,在第一象限f 3(x )的图象上存在一点(2,f (2))在f 2(x)图象的上方. ∴f 2(x )与f 3(x)的图象在第一象限有两个交点,即f(x)=fA 有两个正数解. 因此,方程f(x)=fA 有三个实数解. 【证法二】由f(x)=fA ,得x 2+x 8=a 2+a8, 即(x －a )(x+a －ax8)=0,得方程的一个解x 1=a. 方程x+a －ax8=0化为ax 2+a 2x －8=0, 由a >3,△=a 4+32a >0,得 x 2=a a a a 23242+--, x 3=aa a a 23242++-,∵x 2<0, x 3>0, ∴x 1≠ x 2,且x 2≠ x 3.若x 1= x 3,即a =aaa a 23242++-,则3a 2=a a 324+, a 4=4a ,得a =0或a =34,这与a >3矛盾, ∴x 1≠ x 3. 故原方程f(x)=fA 有三个实数解.（21）【证明】(1) ∵棱台DEF —ABC 与棱锥P —ABC 的棱长和相等, ∴DE+EF+FD=PD+OE+PF. 又∵截面DEF ∥底面ABC,∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°, ∴P —ABC 是正四面体. 【解】(2)取BC 的中点M,连拉PM,DM.AM. ∵BC ⊥PM,BC ⊥AM, ∴BC ⊥平面PAM,BC ⊥DM, 则∠DMA 为二面角D —BC —A 的平面角. 由(1)知,P —ABC 的各棱长均为1, ∴PM=AM=23,由D 是PA 的中点,得 sin ∠DMA=33=AM AD ,∴∠DMA=arcsin 33. (3)存在满足条件的直平行六面体.棱台DEF —ABC 的棱长和为定值6,体积为V.设直平行六面体的棱长均为21,底面相邻两边夹角为α, 则该六面体棱长和为6, 体积为81sinα=V .∵正四面体P —ABC 的体积是122,∴0<V<122,0<8V<1.可知α=arcsim(8V) 故构造棱长均为21,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求. （22）【解】(1) a 1=1OP 2=100,由S 3=23(a 1+a 3)=255,得a 3=3OP 3=70.由 2510022y x +=1 ,得x 23=60 X 23+y 23=70y 23=10∴点P 3的坐标可以为(215, 10).(2)【解法一】原点O 到二次曲线C:12222=+by a x (a>b>0)上各点的最小距离为b,最大距离为a . ∵a 1=1OP 2=a 2, ∴d<0,且a n =n OP 2=a 2+(n －1)d≥b 2,∴122--n a b ≤d<0. ∵n≥3,2)1(-n n >0∴S n =n a 2+2)1(-n n d 在[122--n a b ,0)上递增,故S n 的最小值为n a 2+2)1(-n n ·122--n a b =2)(22b a n +.【解法二】对每个自然数k(2≤k≤n),由 x 2k +y 2k =a 2+(k －1)d,解得y2k =222)1(b a dk b ---22a x k +22b y k =1∵0< y 2k ≤b 2,得122--k ab ≤d<0 ∴122--n a b ≤d<0 以下与解法一相同.(3)解法一】若双曲线C:22a x －22b y =1,点P 1(a ,0),则对于给定的n, 点P 1, P 2,…P n 存在的充要条件是d>0. ∵原点O 到双曲线C 上各点的距离h ∈[a ,+∞),且1OP =a 2,∴点P 1, P 2,…P n 存在当且仅当n OP 2>1OP 2,即d>0.【解法二】若抛物线C:y 2=2x ,点P 1(0,0),则对于给定的n, 点P 1, P 2,…P n 存在的充要条件是d>0.理由同上【解法三】若圆C:(x －a )+y 2=a 2(a ≠0), P 1(0,0),则对于给定的n, 点P 1, P 2,…P n 存在的充要条件是0<d≤142-n a .∵原点O 到圆C 上各点的最小距离为0,最大距离为2a ,且1OP =0, ∴d>0且n OP 2=(n －1)d≤4a 2.即0<d≤142 n a .。

2004年普通高等学校招生全国统一考试数学（理科）北京卷考试说明（北京教育考试院编）Ⅰ.考试性质普通高等学校招生全国统一考试是为高校招生而进行的选拔性考试。

考试的指导思想是：有助于高等学校选拔新生，有助于中学实施素质教育，有助于培养学生的创新精神与实践能力。

试题应有较高的信度、效度、必要的区分度和适当的难度。

Ⅱ.考试要求数学科高考旨在考查中学数学的基础知识、基本技能、基本思想和方法，考查逻辑思维能力、运算能力、空间想象能力以及分析和解决问题的能力。

根据原国家教育委员会1990年颁布的《全日制中学数学教学大纲（修订本）》和有关中学数学教学内容的调整意见，对考试内容的知识要求和能力要求说明如下：1．知识要求对知识的要求由低到高分为了解、理解、掌握、灵活和综合运用四个层次，且高一级的层次要求包含低一级的层次要求。

了解、理解、掌握为对知识的基本要求（详见Ⅳ.考试内容），灵活和综合运用不对应具体的考试内容：（1）了解（A）：对所列知识内容有初步的认识，会在有关的问题中进行识别和直接应用。

（2）理解（B）：对所列知识内容有理性的认识，能够解释、举例或变形、推断，并利用所列知识解决简单问题。

（3）掌握（C）：对所列知识内容有较深刻的理性认识，形成技能，并能利用所列知识解决有关问题。

（4）灵活和综合运用（D）系统地把握知识的内在联系，并能运用相关知识分析、解决较复杂的或综合性的问题。

2．能力要求（1）逻辑思维能力：会对问题或资料进行观察、比较、分析、综合、抽象和概括；会用演绎、归纳和类比进行推理；能够合乎逻辑、准确、清晰地进行表述。

（2）运算能力：会根据概念、公式、法则正确地对数、式、方程进行变形和运算；能分析条件，寻求与设计合理、简捷的运算途径，能根据要求对数据进行估计，并能进行近似计算。

（3）空间想象能力：能根据条件画出正确的图形，根据图形想象出直观形象；能正确地分析出图形中的基本元素及其相互关系；能对图形进行分解、组合与变形。

高中物理学习材料（灿若寒星**整理制作）2004年普通高等学校招生全国统一考试理科综合能力测试（北京卷）本试卷分第I卷（选择题）和第II卷（非选择题）两部分，第I卷1至5页，第II卷6至16页。

考试结束，将试题卷和答题卡一并交回。

第I卷（选择题共21题每题6分共126分）注意事项：1. 答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题卷上。

在下列各题的四个选项中，只有一个选项是最符合题目要求的。

以下数据可供解题时参考：原子量：H 1 C 12 N 14 O 16 Mg 24 P 31 Cl 35.5 K 39 Cu 641. 在以下描述中，可以将病毒与其他微生物相区别的是A. 能够使人或动、植物患病B. 没有细胞核，仅有核酸C. 具有寄生性D. 由核酸和蛋白质装配进行增殖2. 新生儿小肠上皮细胞通过消耗ATP，可以直接吸收母乳中的免疫球蛋白质和半乳糖。

这两种物质分别被吸收到血液中的方式是A. 主动运输、主动运输B. 内吞、主动运输C. 主动运输、内吞D. 被动运输、主动运输3. 人类21三体综合症的成因是在生殖细胞形成的过程中，第21号染色体没有分离。

若女患者与正常人结婚后可以生育，其子女患该病的概率为A. 0B. 41C. 21 D. 1 4. 在相同光照和温度条件下，空气中CO 2含量与植物光合产量（有机物积累量）的关系如图所示。

理论上某种C 3植物能更有效地利用CO 2，使光合产量高于m 点的选项是A. 若a 点在a 2，b 点在b 2时B. 若a 点在a 1，b 点在b 1时C. 若a 点在a 2，b 点在b 1时D. 若a 点在a 1，b 点在b 2时0 a 1 a a 2 b 1 b b 2 二氧化碳含量 光合 产 量m5. 转基因抗虫棉可以有效地用于棉铃虫的防治。

2004年普通高等学校招生全国统一考试英语第一卷（三部分，共115分）第一部分：听力理解（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话你将听一遍。

例：How much is the shirt ?A. £19.5.B. £9.15.C. £9.18.答案是B.1．What do we learn about the man ?A．He slept well on the plane .B．He had a long trip .C．He had a meeting.2．Why will the woman stay home in the evening ?A．To wait for a call .B．To watch a ball game on TV .C．To have dinner with a friend .3．What gift will the woman probably get for Mary ?A．A school bag . B．A record . C．A theatre ticket . 4．What does the man mainly do in his spare time ?A．Learn a language . B．Do some sports . C．Play the piano .5．What did the woman like doing when she was young ?A．Riding a bicycle with friends .B．Traveling the country .C．Reading alone .第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

2004年普通高等学校招生全国统一考试数学（文史类）（老课程）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至10页。

考试结束后，将本试卷和答题卡一并交回。

第I 卷参考公式：三角函数的和差化积公式)]sin()[sin(21cos sin βαβαβα-++=)]sin()[sin(21sin cos βαβαβα--+= )]cos()[cos(21cos cos βαβαβα-++= )]cos()[cos(21sin sin βαβαβα--+-=一、选择题 （1）设集合(){}22,1,,M x y xy x R y R =+=∈∈，(){}2,0,,N x y xy x R y R =-=∈∈，则集合MN 中元素的个数为（ ）A ．1B ．2C ．3D ．4（2）函数sin2xy =的最小正周期是（ ） A ．2πB ．πC ．2πD ．4π(3) 记函数13xy -=+的反函数为()y g x =，则(10)g =（ ） A ． 2B ． 2-C ． 3D ． 1-(4) 等比数列{}n a 中，29,a = 5243a =，则{}n a 的前4项和为（ ）A ． 81B ． 120C ．168D ． 192正棱台、圆台的侧面积公式l c c S )(21+'=台侧其中c ′、c 分别表示上、下底面周长，l 表示 斜高或母线长 台体的体积公式334R V π=球 其中R 表示球的半径(5) 圆2240x y x +-=在点(P 处的切线方程是（ ）A ． 20x +-=B ． 40x +-=C ． 40x -+=D ． 20x +=(6) 61x ⎫⎪⎭展开式中的常数项为（ ）A ． 15B ． 15-C ．20D ． 20-(7) 设复数z 的幅角的主值为23π2z =（ ）A ． 2--B ． 2i -C ． 2+D ． 2i(8) 设双曲线的焦点在x 轴上，两条渐近线为12y x =±，则双曲线的离心率e =（ ）A ． 5B ．C ．2 D ． 54(9) 不等式113x <+<的解集为（ ）A ． ()0,2B ． ()()2,02,4-C ． ()4,0-D ． ()()4,20,2--(10) 正三棱锥的底面边长为2，侧面均为直角三角形，则此三棱锥的体积为（ ）A ．B ．C ．3D ．(11) 在ABC 中，3,4AB BC AC ===，则边AC 上的高为（ ）A ．B ．C ．32D ．(12) 4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（ ）A ． 12 种B ． 24 种C 36 种D ． 48 种第Ⅱ卷二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中横线上. (13) 函数)1(log 21-=x y 的定义域是 .(14) 用平面α截半径为R 的球，如果球心到平面α的距离为2R，那么截得小圆的面积与球 的表面积的比值为 . (15) 函数)(cos 21sin R x x x y ∈-=的最大值为 . (16) 设P 为圆122=+y x 上的动点，则点P 到直线01043=--y x 的距离的最小值为 .三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. (17)（本小题满分12分）解方程.012242=--+x x(18) （本小题满分12分）已知α为锐角，且αααααα2cos 2sin sin cos 2sin ,21tan -=求的值.(19) （本上题满分12分）设数列}{n a 是公差不为零的等差数列，S n 是数列}{n a 的前n 项和，且,9221S S =244S S =，求数列}{n a 的通项公式.20．（本小题满分12分）某村计划建造一个室内面积为800m 2的矩形蔬菜温室，在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地。

2004年普通高等学校招生全国统一考试理科综合能力测试（上海卷）（理科使用）本试卷分第Ⅰ卷和第Ⅱ卷两部分，全卷共12页，满分为150分，考试时间为120分钟。

第Ⅰ卷（共72分）一、李斌，中专毕业后进入上海液化压泵厂工作。

23年来，他在工人岗位上刻苦钻研，勇于创新，无私奉献，成为高级技师和公认的数控机床专家，被誉为“知识工人的楷模”。

1．李斌现象说明了，在什么是人才的表述上，下列最恰当的是（）。

A．人才是指极少数作出杰出贡献的人B．人才是指在某一领域得过奖的人C．人才是指高学历、高职称的人D．人才是指具有一定知识或技能，能进行创造性劳动并作出积极贡献的人2．由于李斌的品牌效应，上海液压泵厂近年来接到了大量定单，国家重点项目，专用设备项目相继找上门，去年销售额同比增加12.6%。

这说明在经济和社会发展中，人才是第一资源，这一观点反映了（）。

①劳动者是生产力的决定性因素②劳动者是生产力发展水平的标志性因素③人才是生产力发展的唯一要素④科学技术和劳动者结合能转化为第一生产力A．②④ B．③④ C．①④ D．①③3．李斌的经历告诉我们，人才是多种多样的，每个人都应该立志成为某一方面的人才，实现人生的应有价值。

为此，我们一定要（）。

①考上名牌大学②认识自己的个性特点，确定成才方向③选择热门专业④把个人机遇与国家、民族机遇联系起来A．①③ B．②④ C．②③ D．①④二、中国民主政治建设是一个渐进的历史发展过程，中国共产党致力于建立和完善中国特色的社会主义民主政治制度，对实现中化民族的伟大复兴有着极为深远的意义和影响。

4．以孙中山为代表的资产阶级革命派创立的中华民国，在政治体制方面效仿的西方国家是（）。

A．美国 B.英国 C.俄国 D.德国5．中国共产党领导的多党合作和政治协商制度是我国的基本政治制度，其形成可以追溯到（）。

A．1949年 B．1954年 C．1956年 D．1978年6．首次明确规定人民代表大会制度为我国根本政治制度的法律文件是（）。

2004年普通高等学校招生全国统一考试（老课程）文科综合能力测试本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第Ⅰ卷注意事项：1．答第I卷前，考生务必将自己姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

3．本卷共35小题，每小题4分，共140分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

求真务实是中华民族的优良传统，中国共产党人继承和发扬这种优良传统。

以胡锦涛同志为总书记的中共中央突出地强调要“大力弘扬求真务实精神，大兴求真务实之风”。

回答26-27题。

26．我国古代思想家十分重视实践和认识之间的关系，汉代思想家王充在《论衡》中说过：“知屋漏者在宇下，知政失者在草野。

”这句话表明①实践是认识的来源②认识对象不会“自言共明”③实践就是每件事都亲历亲为④实践水平越高，人的认识能力就越强A．①②B．②③C．①③D．②④27．强调求真务实，就必须坚持“不唯书、不唯上、只唯实”，这意味着A．根据自己的需要决定是否听从上级指示B．书本知识对于认识事物没有价值C．不必强调理论创新D．要一切从实际出发，实事求是2003年我国信息产业增加值完成7090亿元，全行业经济效益总体指标高出全国水平10个百分点。

同年全国电话用户总数居世界首位，电子产品出口增长52%，出口额已接近全国外贸出口总额的1/3。

回答28-29题。

28．上述材料表明在我国国民经济发展中，信息产业①有效促进了经济增长②具有巨大的市场需求③将会大规模增加就业④将逐步取代传统产业A．①②B．③④C．①④D．②③29．我国信息产业产品出口高速增长的主要原因是A．电子信息产品世界市场需求旺盛B．我国商品市场已经对外开放C．我国电子信息产品具有一定的国际竞争力D．我国大型电子企业具有垄断市场的实力伊拉克问题是近年来国际政治的热点问题。