浙江省杭州市2019年中考数学一轮复习第一章数与式第六节数的开方与二次根式同步测试(含答案)

专题6 数的开方和二次根式一、选择题1. (浙江杭州，1，3分)9＝( )A ．2B ．3C ．4D ．5 【答案】B ．【逐步提示】本题考查了二次根式的性质，解题的关键是能利用a a =2(a ＞0)进行解答，首先应将被开方数9写成32，再利用“a a =2(a ＞0)”即可锁定答案．【解析】因为9＝23＝3，故选择B ．【解后反思】本题亦可以理解为求9的算术平方根，根据算术平方根的定义进行切入思考与计算：看什么正数的平方等于9，这个正数就是9的算术平方根．另外，二次根式实质上就是非负数的算术平方根，熟练地掌握二次根式的性质：(1)2)(a ＝a (a ≥0)；(2)2a ＝a ＝⎩⎨⎧<-≥)0()0(a a a a ，是进行二次根式化简求值的基础．【关键词】二次根式；二次根式的求值；算术平方根2.(浙江杭州，5，3分)下列各式的变形中，正确的是( ) A ．x 2·x 3＝x 6B ．x x =2C ．(x 2－x 1)÷x ＝x －1 D ．x 2－x ＋1＝(x －21)2＋41 【答案】B ．【逐步提示】本题考查了代数式的恒等变形，解题的关键是掌握整式的乘除法法则、二次根式的性质、及完全平方公式的特点．解题时，先按同底数幂乘法法则、整式乘除法法则计算A ．C 选项的式子，判断这两个选项的变形的正确性；再根据完全平方式的特点，对D 选项的式子进行变形，从而判断选项D 的正确性；最后根据二次根式性质判断B 选项的正确性，从而轻松解题． 【解析】∵x 2·x 3＝x 2＋3＝x 5，x x =2，(x 2－x 1)÷x ＝(x 2－x 1)·x 1＝x －21x，x 2－x ＋1＝x 2－x ＋41＋43＝(x －21)2＋43，∴只有选项B 正确，故选择B ． 【解后反思】本题是代数式的有关运算，涉及到整式的运算、二次根式的性质，分式的运算．只要熟练地掌握相关的运算法则与性质，对各个选项的变形逐一判断，即可得到正确答案．四个选项的变形，分别考查了代数式的四个领域：同底数幂相乘，底数不变，指数相加，即：a m ×a n =a m +n(m 、n 都是正整数)；整式除法，转化为乘法，然后利用分式乘法法则进行计算；配方法得掌握完全平方公式的结构特征：前平方、后平方、积的2倍在中间，就不难进行代数式的配方变形．【关键词】代数式的恒等变形；同底数的乘除法；二次根式的性质；配方法；整式的除法3.(浙江宁波，4，4分)使二次根式1x -有意义的x 的取值范围是( )A. x ≠1B. x > 1C. x ≤1D. x ≥1 【答案】D【逐步提示】本题考查了二次根式的概念，解题的关键是正确理解二次根式有意义的条件. 先根据二次根式有意义的条件建立关于x 的不等式，再解这个不等式确定x 的取值范围． 【解析】根据题意，得10x -≥，解得x ≥1，故选择D .【解后反思】形式)0(≥a a 的式子是二次根式，因此二次根式的被开方数a 应满足条件a ≥0. 解答与二次根式概念有关的问题通常是根据这个条件建立不等式来求解． 【关键词】二次根式 4.(重庆B ，7，4分)若二次根式2a -有意义，则a 的取值范围是( ) A ．a ≥2 B ．a ≤2 C ．a ＞2 D ．a ≠2 【答案】A【逐步提示】a 所在的代数式为二次根式，必须使被开方数为非负数.【解析】由题意可知a －2≥0，解得a ≥2. 故选A .【解后反思】求代数式中字母的取值范围，要看给出的代数式是整式、分式、二次根式，还是有关代数式的组合，然后结合整式、分式及二次根式成立的条件判断即可. 【关键词】二次根式 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35.36.37.38.39.二、填空题1.（山东聊城，13，3分）计算：278132⋅÷ =【答案】12【逐步提示】第一步直接利用二次根式乘除法法则把二次根式乘除法转化为被开方数的乘除法, 第二步计算二次根式乘除法, 第三步化简二次根式.278132⋅81827=272=916=34=12323⨯÷⨯⨯⨯⨯.故填12 .【解后反思】考查了二次根式的乘法，解题的关键是正确运用二次根式的乘法法则及二次根式的化简．二次根式相乘，把被开方数相乘，根指数不变；二次根式相乘，把被开方数相乘，根指数不变．【关键词】二次根式；二次根式乘法；二次根式除法；；2.（山东青岛，9，33282= .【答案】2【逐步提示】先计算分子中的减法，再进行除法运算.【详细解答】解：原式42222222，故答案为2.【解后反思】1.二次根式混合运算顺序：先乘方，再乘除，最后加减；2.二次根式运算的结果一般要化为最简二次根式；3.每个根式都可看成“单项式”，多项式的乘法法则及乘法公式仍然适用．【关键词】二次根式的混合运算3. (山东威海，14，3)188_____________.2【逐步提示】首先化简二次根式使其成为最简二次根式，然后合并同类二次根式．18832222=2 .【解后反思】一个二次根式，满足以下几个条件就被称为最简二次根式：(1) 被开放数不含有开得尽的因数或因式；(2)被开方数中不含分母；(3)分母中不含根号．同类二次根式：化简成最简二次根式之后，被开方数相同的二次根式称为同类二次根式．二次根式的加减步骤是先化简二次根式，然后再合并同类二次根式，法则类似于合并同类项．【关键词】二次根式；最简二次根式；同类二次根式，二次根式的加减4. (天津，14，3分)计算5353+)(-)的结果等于 .【答案】2【逐步提示】本题考查了二次根式的运算．利用乘法公式中的平方差公式(a+b)(a－b)=a2－b2，进行运算，合并化简即可．【解析】(53)(53)+-=22(5)(3)-=５－3=２，故答案为2.【解后反思】本题考查了二次根式的混合运算以及平方差公式，能根据算式的特点利用平方差公式简化运算是解题的关键．【关键词】二次根式的运算；平方差公式5. （ 四川省巴中市，9，3分）下列二次根式中，与3是同类二次根式的是（ ）A. 18B.13C.24D.0.3 【答案】B.【逐步提示】本题考查了二次根式的化简，以及同类二次根式的概念，解题的关键是应用二次根式的性质，将二次根式进行化简．先将各二次根式化简成最简二次根式，再根据同类二次根式的定义进行选择. 【详细解答】解：18=32，13=133，24=26，0.3=13010，其中只有133 与3是同类二次根式，故选择B.【解后反思】一个二次根式是否为最简二次根式，必须满足两个条件（1）根号内不含有开方开得尽的因数或因式，（2）二次根式的根号内不含有分母；而同类二次根式是指把二次根式化为最简二次根式后，被开方数相同的就是同类二次根式，被开方数不同的就不是同类二次根式， 【关键词】最简二次根式；同类二次根式；6. （ 四川南充，2，3分）下列计算正确的是（ ）A ．1223=B ．3322= C ．3x x x -=- D ．2x x = 【答案】A【逐步提示】本题考查了二次根式的化简、商的算术平方根，解题的关键是熟练掌握上述运算法则．根据对应的运算法则逐个计算再作出判断. 【详细解答】解：124323=⨯=，选项A 正确；336222==，选项B 错误； 因为3x -≥0，则x ≤032x x x x x -=-=--，选项C 2x x =，选项D 错误；故选择A ．【解后反思】此题主要考查了二次根式的化简，正确掌握二次根式的性质是解题关键．【关键词】二次根式的化简；二次根式的乘法；二次根式的除法7（四川省自贡市，3，4分）下列根式中，不是最简二次根式的是 A ．10 B ．8 C ．6 D ．2【答案】B【逐步提示】看被开方数是否含有能开方的因式，若含有，则不是最简二次根式，若不含有则是最简二次根式. 【详细解答】解：B 选项中被开方数8可以分解为4×2，4可以开平方，所以B 不是最简二次根式，故选择B. 【解后反思】二次根式的化简主要运用二次根式的乘除法法则及二次根式的性质进行运算：1. 乘法法则：(a 0,b 0)a b ab •=≥≥.2．除法法则：(a 0,b 0)aa b b÷=≥>. 3．a a =2.【关键词】二次根式的化简8.(浙江金华，12，4分)能够说明“2x x =不成立．．．”的x 的值是 (写出一个即可). 【答案】如-1等(只要填一个负数即可)【逐步提示】认真审题，根据2x x =成立的条件，确定不成立的x 的值．【解析】因为2x x =成立的条件为x ≥0,所以“2x x =不成立．．．”的x 的值是所有负数，答案不唯一，故答案可以为如-1等(只要填一个负数即可) .【解后反思】根据公式成立的条件确定出公式不成立的条件． 【关键词】二次根式9.(浙江宁波，13，4分)实数-27 的立方根是 . 【答案】-3【逐步提示】本题考查了立方根的概念，解题的关键是掌握利用逆运算求立方根的方法．利用立方和开立方运算是互逆运算进行求解．【解析】由于(-3)3=-27，所以-27 的立方根是-3，故答案为-3 .【解后反思】任何实数的立方根只有一个；正数的立方根是正数，负数的立方根是负数，零的立方根是零．求一些特殊实数的立方根也是利用数的立方的逆运算来求的． 【关键词】 立方根的概念及求法10.(浙江衢州，12，4分)二次根式3x -中字母x 的取值范围是＿＿＿.【答案】x ≥3.【逐步提示】由二次根式的被开方式是非负数，列出不等式求解. 【解析】依题意，得x －3≥0，解得x ≥3，故答案为x ≥3.【解后反思】正确理解二次根式的被开方式是非负数，是顺利求解此类问题的关键. 【关键词】二次根式的意义，不等式.11.(浙江舟山，12，4分)二次根式x －1中，字母x 的取值范围是 . 【答案】x ≥1【逐步提示】本题考查了二次根式的概念，解题的关键是根据二次根式有意义的条件建立关于x 的不等式求解. 二次根式有意义，必须满足被开方数是非负数.【解析】由题意，得x －1≥0，∴x ≥1，故答案为 x ≥1 .【解后反思】在一般的函数关系中自变量的取值范围主要考虑以下四种情况：⑴函数关系式为整式形式：自变量取值范围为任意实数；⑵函数关系式为分式形式：分母≠0；⑶函数关系式含算术平方根：被开方数≥0；⑷函数关系式含指数为0的幂的形式：底数≠0．【关键词】函数定义及其取值范围；解一元一次不等式12.. （ 四川乐山，14，3分）在数轴上表示实数a 的点如图7所示，化简2(5)2a a -+-的结果为___ _．图7a 52【答案】3．【逐步提示】观察数轴易得2＜a ＜5，再将2(5)2a a -+-化简获解．【详细解答】解：由数轴得2＜a ＜5，∴ 2(5)2a a -+-=5-a+a-2=5-2=3，故答案为3．【解后反思】(1)绝对值：正数的绝对值是它本身，负数的绝对值等于它的相反数，0的绝对值是0．(2) 二次根式有意义的条件是：被开方数必须是非负数．否则二次根式无意义． 【关键词】数轴；绝对值；二次根式 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39.三、解答题1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.。

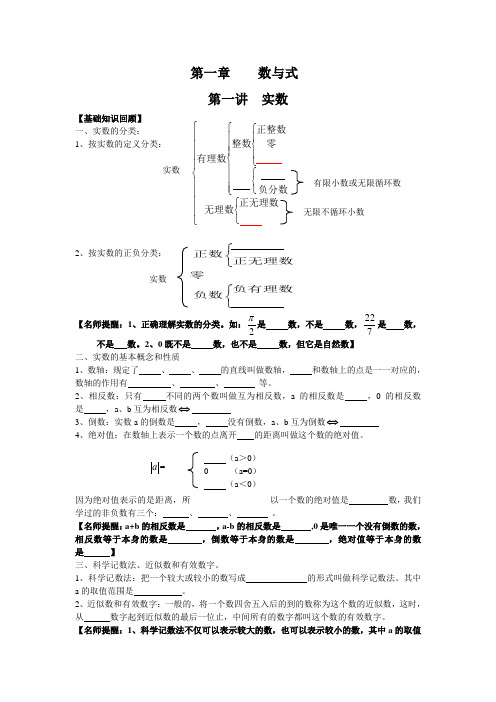
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类： 1、按实数的定义分类： 实数 有限小数或无限循环数2、按实数的正负分类：实数【名师提醒：1、正确理解实数的分类。

如：2π是 数，不是 数，722是 数，不是 数。

2、0既不是 数，也不是 数，但它是自然数】二、实数的基本概念和性质1、数轴：规定了 、 、 的直线叫做数轴， 和数轴上的点是一一对应的，数轴的作用有 、 、 等。

2、相反数：只有 不同的两个数叫做互为相反数，a 的相反数是 ，0的相反数是 ，a 、b 互为相反数⇔3、倒数：实数a 的倒数是 ， 没有倒数，a 、b 互为倒数⇔4、绝对值：在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。

a =因为绝对值表示的是距离，所以一个数的绝对值是 数，我们学过的非负数有三个： 、 、 。

【名师提醒：a+b 的相反数是 ，a-b 的相反数是 ,0是唯一一个没有倒数的数，相反数等于本身的数是 ，倒数等于本身的数是 ，绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。

1、科学记数法：把一个较大或较小的数写成 的形式叫做科学记数法。

其中a 的取值范围是 。

2、近似数和有效数字：一般的，将一个数四舍五入后的到的数称为这个数的近似数，这时，从 数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字。

【名师提醒：1、科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 （a ＞0） （a ＜0） 0 （a=0）范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）。

数的开方与二次根式主备人 刘敖川 审核人 张丽丽【考点链接】1．式子)0(≥a a 叫做二次根式．注意被开方数a 只能是 ．2． 的二次根式，叫做最简二次根式．3．化成最简二次根式后，被开方数 几个二次根式，叫做同类二次根式．4．二次根式的性质 ：⑴ ； ⑵ ()=2a （a ≥0）； ⑶=2a ； （4）=ab （0,0≥≥b a ）； （5）=b a （0,0>≥b a ）. 【典例精析】例1 （1x 取值范围是________．（2）已知a例2： ）A B C例3：若a ，b 分别表示10的整数部分与小数部分，求41++b a 的值【中考演练】1_______， -164的立方根为_______．2x 的取值范围是 （ ）A ．13x >B ．13x >- C ． 13x ≥ D ．13x ≥-3．（10上海）计算：2=__________．4. 若无理数a 满足不等式14<<a ，请写出两个符合条件的无理数_____________.5．（10长春）计算：（1）54-= _____________.（2+2）=_________．6．下列叙述中正确的是（ ）A ．正数的平方根不可能是负数B ．无限小数都是无理数C ．实数和实数上的点一一对应D ．带根号的数是无理数7．（10年福州市）下列各式中属于最简二次根式的是（ ）A B C8．（10年恩施自治州）若m 的值为（ ） A ．20511315 (32688)B C D9．（10海淀）合并的二次根式为（ ）A B C D 10．估算31－2的值（ ）A ．在1和2之间B ．在2和3之间C ．在3和4之间D ．在4和5之间11．若ab<0，化简二次根式321b a a-的结果是：（ ）. A.b b B.-b b C. b b - D. -b b -【课后作业】1．函数y=11+x 的自变量的取值范围是 . A.x≥-1 B. x>-1 C. x≠1 D. x≠-12．函数2-=x y 中，自变量x 的取值范围是 .3．（2010·绵阳）要使1213-+-x x 有意义，则x 应满足（ ）． A ．21≤x ≤3 B ．x ≤3且x ≠21 C ．21＜x ＜3 D ．21＜x ≤34．（2010，安徽芜湖）要使式子a 有意义，a 的取值范围是（ ） A ．a≠0 B ．a>－2且a≠0C ．a>－2或a≠0D ．a≥－2且a≠0 5．（2010年常州）下列运算错误的是（ ）．A = B. = = D.2(2=6．下列各组中的两个根式是同类二次根式的是（ ）A ．52x 和3xB ．12ab 和13abC ．x 2y 和xy 2D ． a 和1a 27．下列二次根式中，是最简二次根式的是（ ）A ．8xB ．x 2－3C ．x －y x D ．3a 2b 8．在27 ．112 ．112中与 3 是同类二次根式的个数是（ ） A ．0 B ．1 C ．2 D ．39.（2010年安徽）计算：=-⨯263_____:；=+312______10=___ __．11．（2010的的算术平方根是 ．13．（10年永州) 下列判断正确的是（ ）A ． 23＜3＜2B ． 2＜2＋3＜3C ． 1＜5－3＜2D ． 4＜3·5＜514．（2007===请你将发现的规律用含自然数n (n ≥1)的等式表示出来__________________________． 在实数范围内因式分解:x x 53-= ;15．计算（1）8132182+- （2）2543122÷⨯（3）)92913(25523x x x x +- （4）)622554(83--⨯（5）301007)6t a n 30)3-⎛⎫-- ⎪⎝⎭o（6）计算：|345tan |32)31()21(10-︒-⨯+--。

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……第六节 数的开方与二次根式姓名：________ 班级：________ 用时：______分钟1. (2018·辽宁抚顺中考)二次根式1－x 在实数范围内有意义，则x 的取值范围是( ) A ．x≥1B ．x≤1C ．x ＞1D ．x ＜12．(2018·浙江杭州中考)下列计算正确的是( ) A.22＝2 B.22＝±2 C.42＝2D.42＝±23．(2018·云南曲靖中考)下列二次根式中能与23合并的是( ) A.8 B.13C.18D.94．(2018·江苏泰州中考)下列运算正确的是( ) A.2＋3＝ 5 B.18＝2 3 C.2·3＝ 5D.2÷12＝2 5．(2018·重庆中考A 卷)估计(230－24)·16的值应在( ) A ．1和2之间 B ．2和3之间 C ．3和4之间D ．4和5之间6．式子x －2x －3有意义的条件是__________________．7．(2018·山东潍坊中考)用教材中的计算器进行计算，开机后依次按下，把显示结果输入右侧的程序中，则输出的结果是______.8．(2018·广东广州中考)如图，数轴上点A 表示的数为a ，化简：a ＋a 2－4a ＋4＝______．9．(2017·四川德阳中考)计算：(25－2)0＋|2－5|＋(－1)2 017－13×45.10．(2018·浙江台州模拟)已知x ＝2－1，求x 2＋3x －1的值．11．已知y ＝2x －5＋5－2x －3，则2xy 的值为( ) A ．－15B ．15C ．－152D.15212．如果一个三角形的三边长分别为1，k ，4，那么化简|2k －5|－k 2－12k ＋36的结果是( ) A ．3k －11 B ．k ＋1 C ．1D ．11－3k13．已知a ，b 分别是6－13的整数部分和小数部分，那么2a －b 的值是( ) A ．3－13 B ．4－13 C.13D ．2＋1314．若关于x 的方程－2x ＋m 2 017－x ＋4 020＝0存在整数解，则正整数m 的所有取值的和为________. 15．已知|a －2 017|＋a －2 018＝a ，则a －2 0172的值是______________． 16．已知a ＝1－3，b ＝1＋3，求2a 2＋2b 2－3ab －a ＋b 的值．17．请在方格内画△ABC，使它的顶点都在格点上，且三边长分别为2，25，412. (1)求△ABC 的面积； (2)求出最长边上的高．18．(2019·创新题)小明在学习《二次根式》后，发现一些含根号的式子可以写成另一个式子的平方，如3＋22＝(1＋2)2.善于思考的小明进行了以下探索：设a＋b2＝(m＋n2)2(其中a，b，m，n均为整数)，则有a＋b2＝m2＋2n2＋2mn 2.∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把类似a＋2b的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：(1)当a，b，m，n均为正整数时，若a＋b3＝(m＋n3)2，用含m，n的式子分别表示a，b，得a＝________，b＝________；(2)利用所探索的结论，找一组正整数a，b，m，n填空：________＋________3＝(________＋________3)2；(3)若a＋43＝(m＋n3)2，且a，m，n均为正整数，求a的值．19．阅读下列材料，回答有关问题：在实数这章中，遇到过2，3，9，12，a这样的式子，我们把这样的式子叫做二次根式，根号下的数叫做被开方数．如果一个二次根式的被开方数中有的因数能开得尽方，可以利用a·b＝a·b(a≥0，b≥0)；a b ＝ab(a≥0，b>0)将这些因数开出来，从而将二次根式化简．当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时，这样的二次根式叫做最简二次根式，例如，13化成最简二次根式是33，27化成最简二次根式是33，几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式叫做同类二次根式，如上面的例子中的13和27就是同类二次根式．(1)请判断下列各式中，哪些是同类二次根式？ 2，75，18，150，127， 3. (2)二次根式中的同类二次根式可以像整式中的同类项一样合并，请计算： 2＋75－18－150＋127－ 3.20．在进行二次根式化简时，我们有时会碰上如53，23，23＋1一样的式子，其实我们还可以将其进一步化简：53＝5×33×3＝533，23＝2×33×3＝63，23＋1＝2×（3－1）（3＋1）＝2（3－1）（3）2－12＝3－1，23＋1还可以用以下方法化简：23＋1＝3－13＋1＝（3）2－123＋1＝（3＋1）（3－1）3＋1＝3－1.以上这种化简的方法叫做分母有理化． (1)请化简25＋3＝________；(2)若a 是2的小数部分则3a＝________；(3)矩形的面积为35＋1，一边长为5－2，则它的周长为________；(4)化简21＋5＋25＋9＋29＋13＋…＋24n－3＋4n＋1.参考答案【基础训练】1．B 2.A 3.B 4.D 5.B6．x≥2且x≠37.7 8.29．解：原式＝1＋5－2－1－5＝－2. 10．解：∵x＝2－1，∴x＋1＝2，∴(x＋1)2＝(2)2＝2，即x2＋2x＋1＝2，∴x2＋2x＝1，∴x2＋3x－1＝x2＋2x＋x－1＝1＋x－1＝2－1. 【拔高训练】11．A 12.A 13.C 14.15 15.2 018 16．解：∵a＝1－3，b＝1＋3，∴a－b＝(1－3)－(1＋3)＝－23，ab＝(1－3)(1＋3)＝－2，∴2a2＋2b2－3ab－a＋b＝2(a－b)2－(a－b)＋ab ＝2(－23)2－(－23)＋(－2)＝22＋2 3.17．解：画图如图所示．(1)S △ABC ＝2.(2)最长边上的高为255.18．解：(1)∵a＋b 3＝(m ＋n 3)2， ∴a＋b 3＝m 2＋3n 2＋2mn 3， ∴a＝m 2＋3n 2，b ＝2mn.(2)答案不唯一，如：设m ＝1，n ＝1， ∴a＝m 2＋3n 2＝4，b ＝2mn ＝2. (3)由题意，得： a ＝m 2＋3n 2，b ＝2mn∵4＝2mn ，且m ，n 为正整数， ∴m＝2，n ＝1或m ＝1，n ＝2，∴a＝22＋3×12＝7或a ＝12＋3×22＝13. 19．解：(1)75＝53，18＝32，150＝210，127＝39， ∴2，18，150是同类二次根式；75，127，3是同类二次根式． (2)原式＝2＋53－32－210＋39－3＝－21210＋3739. 【培优训练】 20．解：(1)5－ 3 (2)32＋3 (3)30＋16 5(4)原式＝2（5－1）5－1＋2（9－5）9－5＋2（13－9）13－9＋…＋2（4n ＋1－4n －3）（4n ＋1）－（4n －3）＝5－1＋9－5＋13－9＋…＋4n ＋1－4n －32＝4n ＋1－12.。

课时训练(四) 数的开方及二次根式夯实基础1.[2017·广安] 要使二次根式在实数范围内有意义,则x的取值范围是()A.x>2B.x≥2C.x<2D.x=22.下列根式中是最简二次根式的是()A.B.C.D.3.[2018·泰州] 下列运算正确的是 ()A.+=B.=2C.·=D.÷=24.关于的叙述,错误的是()A.是有理数B.面积为12的正方形的边长是C.=2D.在数轴上可以找到表示的点5.已知边长为a的正方形的面积为8,则下列说法中错误的是()2 2A.a是无理数B.a是方程x2-8=0的解C.a是8的算术平方根D.a 满足不等式组6.将一组数,,3,2,,…,3按下面的方法进行排列:,,3,2,;3,,2,3,;…若2的位置记为(1,4),2的位置记为(2,3),则这组数中最大的有理数的位置记为()A.(5,2)B.7.[2017·徐州8.[2017·无锡] 计算×的值是9.[2017·常德] 计算:|-2|-= .10.[2018·临沂] 计算:|1-|= .11.计算(+)(-)的结果为.12.已知x1=+,x2=-,则+= .13.[2018·潍坊] 用教材中的计算器进行计算,开机后依次按下 ,把显示结果输入程序中,则输出的结果是.图K4-114.(1)[2017·德阳] 计算:(2-)0+|2-|+(-1)2017-×;(2)[2017·呼和浩特] 计算:--+.15.若x满足|2017-x|+=x,求x-20172的值.16.先化简,再求值:(a2b+ab)÷,其中a=+1,b=-1.34 4 17.在如图K4-2所示的4×3网格中,每个小正方形的边长均为1,正方形的顶点叫网格格点,连结两个网格格点的线段叫网格线段.(1)请你画一个边长为的菱形,并求其面积;(2)若a是图中能用网格线段表示的最大无理数,b是图中能用网格线段表示的最小无理数,求a2-2b2的平方根.图K4-218.已知a=-,b=2-,c=-2.请比较a,b,c的大小.B组·拓展提升19.已知△ABC的三边长分别为a,b,c,则代数式+-= .20.阅读材料:小明在学习了二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2=.善于思考的小明进行了以下探索:设a+b=(m+n)2(其中a,b,m,n均为正整数),则有a+b=m2+2n2+2mn.∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分形如a+b的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:(1)当a,b,m,n均为正整数时,若a+b=(m+n)2,用含m,n的式子分别表示a,b,得a= ,b= ;(2)利用所探索的结论,找一组正整数a,b,m,n填空:+=(+)2;(3)若a+4=(m+n)2,且a,m,n均为正整数,求a的值.参考答案1.B[解析] ∵二次根式有意义,∴2x-4≥0,解得x≥2.故选B.2.B3.D4.A5.D6.C7.28.69.010.-111.-112.1013.7[解析] 32=9,9÷3-=3->1,故输出(3-)(3+)=7.14.解:(1)原式=1+-2-1-=-2.(2)原式=-2--+56 6 =-2--+ =2-1.15.解:由条件知,x-2018≥0,所以x≥2018,|2017-x|=x-2017.所以x-2017+=x,即=2017,所以x-2018=20172,所以x-20172=2018.16.解:原式=ab(a+1)·=ab.当a=+1,b=-1时,原式=(+1)(-1)=2.17.解:(1)略.(2)a==2,b=,∴a2-2b2=16.∴a2-2b2的平方根为±4. 18.解:显然a,b,c都为正数.∵===+, ===2+,===+2,∴<<,∴a>b>c.19.3a-b-c20.解:(1)m2+3n22mn(2)答案不唯一,如:421 1(3)由题意,得a=m2+3n2,4=2mn,∵4=2mn,且m,n为正整数,∴m=2,n=1或m=1,n=2,∴a=22+3×12=7或a=12+3×22=13.7。

浙江省杭州市2019年中考数学一轮复习第一章数与式同步测试含答案第一章 数与式第一节 实数的有关概念姓名：________ 班级：________ 用时：______分钟1．(2018·辽宁葫芦岛中考)如果温度上升10 ℃记作＋10 ℃，那么温度下降5 ℃记作( ) A ．＋10 ℃ B．－10 ℃ C．＋5 ℃ D．－5 ℃ 2．(2018·辽宁沈阳中考)下列各数中是有理数的是( ) A ．π B ．0 C. 2 D.353．(2018·浙江绍兴中考)绿水青山就是金山银山，为了创造良好的生态生活环境，浙江省2017年清理河湖库塘淤泥约116 000 000方，数字116 000 000用科学记数法可以表示为( ) A ．1.16×109B ．1.16×108C ．1.16×107D ．0.116×1094．(2018·山东潍坊中考)生物学家发现了某种花粉的直径约为0.000 003 6毫米，数据0.000 003 6用科学记数法表示正确的是( ) A ．3.6×10－5B ．0.36×10－5C ．3.6×10－6D ．0.36×10－65．(2017·江苏扬州中考)若数轴上表示－1和3的两点分别是点A 和点B ，则点A 和点B 之间的距离是( ) A ．－4B ．－2C ．2D ．46．(2018·浙江嘉兴模拟)数轴上的点A 到原点的距离是6，则点A 表示的数为( ) A ．6或－6B ．6C ．－6D ．3或－37．(2018·湖南邵阳中考)点A 在数轴上的位置如图所示，则点A 表示的数的相反数是________．8．把下列各数填入相应的括号里：0，8，4，3.141 592 6，sin 60°，－2，3，3－1，227，0.101 001 000 1…(两个“1”之间依次多一个“0”)，1.414，－0.0·2·，－7，－π. 正有理数：{ …}； 负有理数：{ …}；正无理数：{ …}； 负无理数：{ …}； 实数：{ …}．9．若实数a 满足a －|a|＝2a ，则( ) A ．a>0B ．a<0C ．a≥0D ．a≤010．将从1开始的连续自然数按以下规律排列：…则2 017在第________行．11．(2019·易错题)若|x|＝3，|y|＝2，且x>y ，求x ＋y 的值．12．深化理解：对非负实数x“四舍五入”到个位的值记为〈x 〉， 即：当n 为非负整数时，如果n －12≤x<n＋12，那么〈x 〉＝n.如：〈0〉＝〈0.48〉＝0，〈0.64〉＝〈1.493〉＝1， 〈2〉＝2，〈3.5〉＝〈4.12〉＝4… 试解决下列问题：(1)填空：①〈π〉＝________(π为圆周率)；②如果〈2x －1〉＝3，那么实数x 的取值范围为________． (2)①当x≥0，m 为非负整数时，求证：〈x ＋m 〉＝m ＋〈x 〉．②举例说明〈x ＋y 〉＝〈x 〉＋〈y 〉不恒成立． (3)求满足〈x 〉＝43x 的所有非负实数x 的值．参考答案【基础训练】1．D 2.B 3.B 4.C 5.D 6.A 7．－28．正有理数：{4，3.141 592 6，227，1.414 …}负有理数：{－2…}正无理数：{8，sin 60°，3，3－1，0.101 001 000 1…(两个“1”之间依次多一个“0”)…} 负无理数：{－7，－π …}实数：{0，8，4，3.141 592 6，sin 60°，－2，3，3－1，227，0.101 001 000 1…(两个“1”之间依次多一个“0”)，1.414，－0.0·2·，－7，－π…} 【拔高训练】 9．D 10.4511．解：由题意得x ＝3，y ＝2或－2， ∴x＋y ＝5或1. 【培优训练】12．解：(1)①3 ②74≤x<94(2)①证明：设〈x 〉＝n ，则n －12≤x<n＋12，n 为非负整数．又(n ＋m)－12≤x＋m<(n ＋m)＋12，且n ＋m 为非负整数，∴〈x ＋m 〉＝m ＋n ＝m ＋〈x 〉．②举反例：〈0.6〉＋〈0.7〉＝1＋1＝2，而〈0.6＋0.7〉＝〈1.3〉＝1，∴〈0.6〉＋〈0.7〉≠〈0.6＋0.7〉， ∴〈x ＋y 〉＝〈x 〉＋〈y 〉不恒成立． (3)令x ＝34k ，则n ＝k.∴〈34k 〉＝k ，∴k－12≤34k<k ＋12，k≥0.∵0≤k≤2，∴k＝0，1，2， ∴x＝0，34，32.第二节 实数的运算与大小比较姓名：________ 班级：________ 用时：______分钟1．(2018·四川自贡中考)计算－3＋1的结果是( ) A ．－2B ．－4C ．4D ．22．(2018·云南昆明中考)下列运算正确的是( ) A ．(－13)2＝9B ．2 0180－3－8＝－1C ．3a 3·2a －2＝6a(a≠0) D.18－12＝ 63．(2017·山东泰安中考)下列四个数：－3，－3，－π，－1，其中最小的数是( ) A ．－π B ．－3C ．－1D ．－ 34．(2017·湖北咸宁中考)下表是我市四个景区今年2月份某天6时的气温，其中气温最低的景区是( )A.潜山公园B ．陆水湖C ．隐水洞D ．三湖连江5．(1)－2＋2.5＝__________，22－8＝________． (2)144的平方根是__________．6．(2018·广西玉林中考)计算：6－(3－5)＝______．7．(2018·湖北黄冈中考)化简(2－1)0＋(12)－2－9＋3－27＝________．8．(2018·四川泸州中考)计算：π0＋16＋(12)－1－|－4|.9．(2019·易错题)计算：(13)－2－(2 019－π)0＋（－3）2－|－2|.10．某天早上，一辆交通巡逻车从A 地出发，在东西走向的公路上巡视，中午到达B 地，如果规定向东行驶为正，向西行驶为负，行驶纪录如下(单位：km )：(1)B 地在A 地的哪个方向，与A 地相距多少千米？ (2)巡逻车在巡逻过程中，离开A 地最远是多少千米？ (3)若每千米耗油0.1 L ，问：共耗油多少升？11．(2017·内蒙古包头中考)a 2＝1，b 是2的相反数，则a ＋b 的值为( ) A ．－3B ．－1C ．－1或－3D ．1或－312．(2018·浙江宁波模拟)若k<90<k ＋1(k 是整数)，则k ＝( )A ．6B ．7C ．8D ．913．(2018·贵州铜仁中考)计算12＋16＋112＋120＋130＋…＋19 900的值为( )A.1100B.99100C.199D.1009914. (2018·湖北恩施州中考)我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”．如图，一位妇女在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量，由图可知，她一共采集到的野果数量为______________个．15．(2019·易错题)化简(π－3.14)0＋|1－22|－8＋(12)－1的结果是______．16．(2017·甘肃天水中考)定义一种新的运算：x*y ＝x ＋2y x ，如：3*1＝3＋2×13＝53，则(2*3)*2＝______．17．为了求1＋3＋32＋33＋…＋3100的值，可令M ＝1＋3＋32＋33＋…＋3100，则3M ＝3＋32＋…＋3100＋3101，此时，3M －M ＝3101－1，所以M ＝3101－12，即1＋3＋32＋33＋…＋3100＝3101－12，仿照以上推理计算：1＋5＋52＋53＋…＋52 018的值是__ __.18．计算：(1)(－2)2－364－(－3)0－(13)－2；(2)(12)－2＋(π－2 015)0＋sin 60°＋|3－2|.19．(2019·创新题)任何实数a ，可用[a]表示不超过a 的最大整数，如[4]＝4，[3]＝1.现对72进行如下操作：72――→第一次[72]＝8――→第二次[8]＝2――→第三次[2]＝1，这样对72只需进行3次操作后变为1.类似地，①对81只需进行______次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是__________．参考答案【基础训练】 1．A 2.C 3.A 4.C 5．(1)0.5 －4 (2)±12 6．8 7.－18．解：原式＝1＋4＋2－4＝3. 9．解：原式＝9－1＋3－2＝9.10．解：(1)＋15－8＋6＋12－4－4－10＝7(km)． 答：B 地在A 地东面，与A 地相距7 km. (2)∵＋15－8＝7(km)， ＋15－8＋6＝13(km)， ＋15－8＋6＋12＝25(km)， ＋15－8＋6＋12－4＝21(km)， ＋15－8＋6＋12－4－4＝17(km)， ＋15－8＋6＋12－4－4－10＝7(km)，∴巡逻车在巡逻过程中，离开A 地最远是25 km.(3)|＋15|＋|－8|＋|＋6|＋|＋12|＋|－4|＋|－4|＋|－10|＝15＋8＋6＋12＋4＋4＋10＝59(km)， 59×0.1＝5.9(L)． 答：共耗油5.9 L. 【拔高训练】 11．C 12.D 13.B14．1 838 15.2 16.2 17.52 019－1418．解：(1)原式＝4－4－1－9＝－10. (2)原式＝4＋1＋32＋2－3＝7－32. 【培优训练】 19．3 255第四节 因式分解姓名：________ 班级：________ 用时：______分钟1．(2019·改编题)将下列多项式因式分解，结果中不含有因式a＋1的是( )A．a2－1B．a2＋aC．a2＋a－2D．(a＋2)2－2(a＋2)＋12．(2018·湖南邵阳中考)将多项式x－x3因式分解正确的是( )A．x(x2－1) B．x(1－x2)C．x(x＋1)(x－1) D．x(1＋x)(1－x)3．(2018·山东东营中考)分解因式：x3－4xy2＝______________________________．4．(2018·浙江杭州中考)因式分解：(a－b)2－(b－a)＝______________________________ 5．(2018·湖南株洲中考)因式分解：a2(a－b)－4(a－b)＝__________________________________．6．(2018·吉林中考)若a＋b＝4，ab＝1，则a2b＋ab2＝______.7．(2018·江苏苏州中考)若a＋b＝4，a－b＝1，则(a＋1)2－(b－1)2的值为________．8．因式分解：(x2－6)2－6(x2－6)＋9.9．(2019·浙江金华模拟)分解因式：m2－25＋9n2＋6mn.10．计算：1252－50×125＋252＝( )A．100 B．150C．10 000 D．22 50011．已知a，b，c是△ABC的三边长，且满足a3＋ab2＋bc2＝b3＋a2b＋ac2，则△ABC的形状是( ) A．等腰三角形B．直角三角形C．等腰三角形或直角三角形D．等腰直角三角形12．(2016·湖北宜昌中考)小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：a－b，x －y，x＋y，a＋b，x2－y2，a2－b2分别对应下列六个字：昌、爱、我、宜、游、美，现将(x2－y2)a2－(x2－y2)b2因式分解，结果呈现的密码信息可能是( )A．我爱美B．宜昌游C．爱我宜昌D．美我宜昌13．如果多项式x2＋px＋12可以分解成两个一次因式的积，那么整数p的值可取多少个( )A．4 B．5C．6 D．814．已知a＝2 002x＋2 003，b＝2 002x＋2 004，c＝2 002x＋2 005，则多项式a2＋b2＋c2－ab－bc－ca 的值为( )A．0 B．1C．2 D．315．(2018·湖北天门模拟)已知ab＝2，a－2b＝－3，则a3b－4a2b2＋4ab3的值为________．16．(2018·天津模拟)分解因式(xy－1)2－(x＋y－2xy)(2－x－y)＝____________________________．17．如图，将一张矩形纸板按照图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m>n，(以上长度单位：cm)(1)观察图形，可以发现代数式2m2＋5mn＋2n2可以因式分解为________；(2)若每块小矩形的面积为10 cm2，四个正方形的面积和为58 cm2，试求图中所有裁剪线(虚线部分)长之和．18．仔细阅读下面例题，解答问题：例题，已知二次三项式x2－4x＋m有一个因式是(x＋3)，求另一个因式以及m的值．解：设另一个因式为(x＋n)，得x2－4x＋m＝(x＋3)(x＋n)，则x2－4x＋m＝x2＋(n＋3)x＋3n.∴⎩⎪⎨⎪⎧n ＋3＝－4，m ＝3n ， 解得n ＝－7，m ＝－21，∴另一个因式为(x －7)，m 的值为－21. 问题：仿照以上方法解答下面问题：已知二次三项式3x 2＋5x －m 有一个因式是(3x －1)，求另一个因式以及m 的值．19．在现今“互联网＋”的时代，密码与我们的生活已经紧密相连，密不可分，而诸如“123456”、生日等简单密码又容易被破解，因此利用简单方法产生一组容易记忆的密码就很有必要了．有一种用“因式分解”法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式：x 3＋2x 2－x －2因式分解的结果为(x －1)(x ＋1)(x ＋2)，当x ＝18时，x －1＝17，x ＋1＝19，x ＋2＝20，此时可以得到数字密码171920.(1)根据上述方法，当x ＝21，y ＝7时，对于多项式x 3－xy 2分解因式后可以形成哪些数字密码？(写出三个)(2)若一个直角三角形的周长是24，斜边长为10，其中两条直角边分别为x ，y ，求出一个由多项式x 3y ＋xy 3分解因式后得到的密码(只需一个即可)；(3)若多项式x 3＋(m －3n)x 2－nx －21因式分解后，利用本题的方法，当x ＝27时可以得到其中一个密码为242834，求m ，n 的值．参考答案【基础训练】1．C 2.D 3.x(x ＋2y)(x －2y)4．(a －b)(a －b ＋1)5．(a －b)(a ＋2)(a －2) 6.4 7.128．解：原式＝(x 2－6－3)2＝(x 2－9)2＝(x ＋3)2(x －3)2.9．解：原式＝(m 2＋6mn ＋9n 2)－25＝(m ＋3n)2－25＝(m ＋3n ＋5)(m ＋3n －5)．【拔高训练】10．C 11.C 12.C 13.C 14.D15．18 16.(y －1)2(x －1)217．解：(1)(m ＋2n)(2m ＋n)(2)依题意得2m 2＋2n 2＝58，mn ＝10.∴m 2＋n 2＝29.∵(m＋n)2＝m 2＋2mn ＋n 2，∴(m＋n)2＝29＋20＝49.∵m＋n>0，∴m＋n ＝7，∴图中所有裁剪线(虚线部分)长之和为42 cm.18．解：设另一个因式为(x ＋n)，则3x 2＋5x －m ＝(3x －1)(x ＋n)．则3x 2＋5x －m ＝3x 2＋(3n －1)x －n.∴⎩⎪⎨⎪⎧3n －1＝5，－n ＝－m ， 解得n ＝2，m ＝2，∴另一个因式为(x ＋2)，m 的值为2.【培优训练】19解：(1)x 3－xy 2＝x(x －y)(x ＋y)，当x ＝21，y ＝7时，x －y ＝14，x ＋y ＝28，可得数字密码是211428，也可以是212814，142128；(2)由题意得⎩⎪⎨⎪⎧x ＋y ＝14，x 2＋y 2＝100，解得xy ＝48， 而x 3y ＋xy 3＝xy(x 2＋y 2)，所以可得数字密码为48100.(3)由题意得x 3＋(m －3n)x 2－nx －21＝(x －3)(x ＋1)(x ＋7)，∵(x－3)(x ＋1)(x ＋7)＝x 3＋5x 2－17x －21，∴x 3＋(m －3n)x 2－nx －21＝x 3＋5x 2－17x －21，∴⎩⎪⎨⎪⎧m －3n ＝5，n ＝17，解得⎩⎪⎨⎪⎧m ＝56，n ＝17. 故m ，n 的值分别是56，17.第三节 整式及其运算姓名：________ 班级：________ 用时：______分钟1．(2018·四川内江中考)下列计算正确的是( )A ．a ＋a ＝a 2B ．(2a)3＝6a 3C ．(a －1)2＝a 2－1D ．a 3÷a＝a 22．(2018·甘肃白银中考)下列计算结果为x 3的是( )A ．x 6÷x 2B ．x 4－xC ．x ＋x 2D ．x 2·x3．(2016·江苏宜兴中考)若二次三项式x 2－mx ＋16是一个完全平方式，则字母m 的值是( )A ．4B ．－4C ．±4D ．±84．(2018·四川乐山中考)已知实数a ，b 满足a ＋b ＝2，ab ＝34，则a －b ＝( ) A ．1 B ．－52 C ．±1 D ．±525．(2018·山东枣庄中考)如图，将边长为3a 的正方形沿虚线剪成两块正方形和两块长方形，若拿掉边长为2b 的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为( )A ．3a ＋2bB ．3a ＋4bC ．6a ＋2bD ．6a ＋4b6．(2018·云南昆明中考)若m ＋1m ＝3，则m 2＋1m ＝______． 7．(2018·湖南邵阳中考)先化简，再求值：(a －2b)(a ＋2b)－(a －2b)2＋8b 2，其中a ＝－2，b ＝12.8．若3x ＝4，9y ＝7，则33x －2y 的值为( ) A.647 B.764C ．－4916 D.1649 9．(2018·浙江绍兴中考)某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品，将这些作品排成一个矩形(作品不完全重合)．现需要在每张作品的四个角落都钉上图钉，如果作品有角落相邻，那么相邻的角落共享一枚图钉(例如，用9枚图钉将4张作品钉在墙上，如图)．若有34枚图钉可供选用，则最多可以展示绘画作品( )A ．16张B ．18张C ．20张D ．21张10．(2019·创新题)定义⎪⎪⎪⎪⎪⎪ab c d 为二阶行列式，规定它的运算法则为⎪⎪⎪⎪⎪⎪a b c d ＝ad －bc.那么当x ＝1时，二阶行列式⎪⎪⎪⎪⎪⎪x ＋1 1－1 x －1的值为______． 11. (2017·江苏南通中考)已知x ＝m 时，多项式x 2＋2x ＋n 2的值为－1，则x ＝－m 时，该多项式的值为______．12．(2019·易错题)先化简，再求值：3a(a 2＋2a ＋1)－2(a ＋1)2，其中a ＝2.13．观察下列关于自然数的等式：32－4×12＝5，①52－4×22＝9，②72－4×32＝13，③…根据上述规律解决下列问题：(1)完成第四个等式：92－4×________2＝________；(2)写出你猜想的第n个等式(用含n的式子表示)，并验证其正确性．14．(2019·创新题)阅读材料：我们知道，4x－2x＋x＝(4－2＋1)x＝3x，类似地，我们把(a＋b)看成一个整体，则4(a＋b)－2(a＋b)＋(a＋b)＝(4－2＋1)(a＋b)＝3(a＋b)．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用：(1)把(a－b)2看成一个整体，合并3(a－b)2－6(a－b)2＋2(a－b)2的结果是________ .(2)已知x2－2y＝4，求3x2－6y－21的值；拓广探索：(3)已知a－2b＝3，2b－c＝－5，c－d＝10，求(a－c)＋(2b－d)－(2b－c)的值．参考答案【基础训练】1．D 2.D 3.D 4.C 5.A 6.77．解：原式＝a 2－4b 2－(a 2－4ab ＋4b 2)＋8b 2＝a 2－4b 2－a 2＋4ab －4b 2＋8b 2＝4ab.当a ＝－2，b ＝12时，原式＝4ab ＝4×(－2)×12＝－4.【拔高训练】8．A 9.D 10.1 11.312．解：原式＝3a 3＋6a 2＋3a －2(a 2＋2a ＋1)＝3a 3＋6a 2＋3a －2a 2－4a －2＝3a 3＋4a 2－a －2，当a ＝2时，原式＝3×23＋4×22－2－2＝36.13．解：(1)4 17(2)第n 个等式为(2n ＋1)2－4n 2＝4n ＋1.验证：左边＝(2n ＋1)2－4n 2＝4n 2＋4n ＋1－4n 2＝4n ＋1＝右边．∴(2n＋1)2－4n 2＝4n ＋1.【培优训练】14．解：(1)－(a －b)2(2)∵x 2－2y ＝4，∴原式＝3(x 2－2y)－21＝12－21＝－9.(3)∵a－2b ＝3，2b －c ＝－5，c －d ＝10，∴a－c ＝－2，2b －d ＝5，∴原式＝－2＋5－(－5)＝8.第五节 分式及其运算姓名：________ 班级：________ 用时：______分钟1．(2018·浙江舟山模拟)把分式xyx 2－y 2中的x ，y 的值都扩大到原来的2倍，则分式的值( )A ．不变B ．扩大到原来的2倍C ．扩大到原来的4倍D ．缩小到原来的122．(2018·辽宁葫芦岛中考)若分式x 2－1x ＋1值为0，则x 的值为( ) A ．0 B ．1 C ．－1 D ．±1 3．(2018·甘肃白银中考)已知a 2＝b 3(a≠0，b≠0)，下列变形错误的是( ) A.a b ＝23B ．2a ＝3b C.b a ＝32 D ．3a ＝2b4．(2018·江苏苏州中考)计算(1＋1x )÷x 2＋2x ＋1x的结果是( ) A ．x ＋1B.1x ＋1C.x x ＋1D.x ＋1x5．(2018·江苏盐城中考)要使分式1x －2有意义，则x 的取值范围是____________． 6．(2018·黑龙江绥化中考)当x ＝2时，代数式(2x ＋1x ＋x)÷x ＋1x的值是______． 7．(2018·江苏泰州中考)化简：(2－x －1x ＋1)÷x 2＋6x ＋9x 2－1.8. (2018·四川广安中考)先化简，再求值：a a ＋1÷(a－1－2a －1a ＋1)并从－1，0，1，2四个数中，选一个合适的数代入求值.9．(2018·四川达州中考)化简代数式：(3x x －1－x x ＋1)÷x x 2－1，再从不等式组⎩⎪⎨⎪⎧x －2（x －1）≥1，①6x ＋10>3x ＋1 ②的解集中取一个合适的整数值代入，求出代数式的值．10．(2019·改编题)已知a 是方程x 2＋x －1＝0的一个根，则2a －a －1a －a的值为( ) A.－1＋52B.－1±52 C ．－1D ．1 11．如图，设k ＝甲图中阴影部分面积乙图中阴影部分面积(a>b>0)，则有( )A ．k>2B ．1<k<2 C.12<k<1 D ．0<k<1212．(2018·浙江金华中考)对于两个非零实数x ，y ，定义一种新的运算：x*y ＝a x ＋b y.若1*(－1)＝2，则(－2)*2的值是________．13. (2018·湖北荆门中考)将数1个1，2个12，3个13，…，n 个1n(为正整数)顺次排成一列： 1，12，12，13，13，13，…，1n ，1n ，…，记a 1＝1，a 2＝12，a 3＝12，…，S 1＝a 1，S 2＝a 1＋a 2， S 3＝a 1＋a 2＋a 3，…，S n ＝a 1＋a 2＋…＋a n ，则S 2 018＝____.14. (2018·四川绵阳中考)已知a ＞b ＞0，且2a ＋1b ＋3b －a ＝0，则b a＝____. 15．(2018·安徽中考)观察以下等式：第1个等式：11＋02＋11×02＝1， 第2个等式：12＋13＋12×13＝1， 第3个等式：13＋24＋13×24＝1， 第4个等式：14＋35＋14×35＝1， 第5个等式：15＋46＋15×46＝1， …按照以上规律，解决下列问题：(1)写出第6个等式：________；(2)写出你猜想的第n 个等式：________(用含n 的等式表示)，并证明．16．(2019·创新题)对于正数x ，规定f(x)＝11＋x ，例如：f(4)＝11＋4＝15，f(14)＝11＋14＝45，求f(2 016)＋f(2 015)＋…＋f(2)＋f(1)＋f(12)＋…＋f(12 015)＋f(12 016)．17. (2018·贵州毕节中考)先化简，再求值：(2a a 2－4－1a －2)÷a a 2＋4a ＋4，其中a 是方程a 2＋a －6＝0的解．18．(2017·四川达州中考)设A ＝a －21＋2a ＋a 2÷(a－3a a ＋1)． (1)化简A ；(2)当a ＝3时，记此时A 的值为f(3)；当a ＝4时，记此时A 的值为f(4)；…解关于x 的不等式：x －22－7－x 4≤f(3)＋f(4)＋…＋f(11)，并将解集在数轴上表示出来．19．阅读下面材料，并解答问题．材料：将分式－x 4－x 2＋3－x 2＋1拆分成一个整式与一个分式(分子为整数)的和的形式． 解：由分母为－x 2＋1，可设－x 4－x 2＋3＝(－x 2＋1)(x 2＋a)＋b ，则－x 4－x 2＋3＝(－x 2＋1)(x 2＋a)＋b ＝－x 4－ax 2＋x 2＋a ＋b ＝－x 4－(a －1)x 2＋(a ＋b)．∵对于任意x ，上述等式均成立，∴⎩⎪⎨⎪⎧a －1＝1，a ＋b ＝3，∴⎩⎪⎨⎪⎧a ＝2，b ＝1. ∴－x 4－x 2＋3－x ＋1＝（－x 2＋1）（x 2＋2）＋1－x ＋1＝（－x 2＋1）（x 2＋2）－x 2＋1＋1－x 2＋1＝x 2＋2＋1－x 2＋1， 这样，分式－x 4·x 2＋3－x 2＋1被拆分成了一个整式x 2＋2与一个分式1－x 2＋1的和． 解答：(1)将分式－x 4－6x 2＋8－x 2＋1拆分成一个整式与一个分式(分子为整数)的和的形式； (2)试说明－x 4·6x 2＋8－x 2＋1的最小值为8.20．设x x 2＋x ＋1＝a(a≠0)，求x 2x 4＋x 2＋1的值．参考答案【基础训练】1．A 2.B 3.B 4.B 5.x≠2 6.37．解：原式＝2（x ＋1）－（x －1）x ＋1÷（x ＋3）2（x ＋1）（x －1）＝x ＋3x ＋1·（x ＋1）（x －1）（x ＋3）2 ＝x －1x ＋3. 8．解：原式＝a a ＋1÷(a 2－1a ＋1－2a －1a ＋1)＝a a ＋1÷a 2－2a a ＋1＝a a ＋1·a ＋1a （a －2） ＝1a －2. 由题意可知a ＋1≠0，a≠0，a －2≠0，所以a≠－1，a≠0，a≠2，当a ＝1时，原式＝－1.9．解：解不等式①得x≤1，解不等式②得x ＞－3，∴不等式组的解集为－3＜x≤1.(3x x －1－x x ＋1)÷x x 2－1＝3x （x ＋1）－x （x －1）（x －1）（x ＋1）·x 2－1x＝3x （x ＋1）－x （x －1）（x －1）（x ＋1）·（x －1）（x ＋1）x＝3(x ＋1)－(x －1)＝3x ＋3－x ＋1＝2x ＋4.∵x≠0，x≠±1，∴当x 取－2时，原式＝2×(－2)＋4＝0.【拔高训练】10．D 11.B 12.－113.2 01732 14.－1＋3215．解：(1)16＋57＋16×57＝1 (2)1n ＋n －1n ＋1＋1n ×n －1n ＋1＝1 证明：∵左边＝1n ＋n －1n ＋1＋1n ×n －1n ＋1＝n ＋1＋n （n －1）＋n －1n （n ＋1）＝1，右边＝1 ∴左边＝右边，∴原等式成立．16．解：∵当x ＝1时，f(1)＝12；当x ＝2时，f(2)＝13，当x ＝12时，f(12)＝23；当x ＝3时，f(3)＝14；当x ＝13时，f(13)＝34，…， ∴f(2)＋f(12)＝1，f(3)＋f(13)＝1，…，∴f(n)＋…＋f(1)＋…＋f(1n)＝f(1)＋(n －1)，∴f(2 016)＋f(2 015)＋…＋f(2)＋f(1)＋f(12)＋…＋f(12 015)＋f(12 016)＝f(1)＋(2 016－1)＝12＋2015＝2 015.5.17．解：原式＝2a －（a ＋2）（a ＋2）（a －2）·（a ＋2）2a ＝a ＋2a .解a 2＋a －6＝0得(a ＋3)(a －2)＝0， 解得a ＝－3或a ＝2， ∵a－2≠0，∴a≠2， ∴a＝－3.当a ＝－3时，原式＝a ＋2a ＝－3＋2－3＝13.18．解：(1)A ＝a －21＋2a ＋a 2÷(a－3aa ＋1) ＝a －2（a ＋1）2÷a （a ＋1）－3aa ＋1 ＝a －2（a ＋1）2·a ＋1a 2－2a ＝a －2（a ＋1）2·a ＋1a （a －2） ＝1a （a ＋1）＝1a 2＋a. (2)∵当a ＝3时，f(3)＝132＋3＝112， a ＝4时，f(4)＝142＋4＝120，a ＝5时，f(5)＝152＋5＝130，… ∴x －22－7－x4≤f(3)＋f(4)＋…＋f(11)， 即x －22－7－x 4≤13×4＋14×5＋…＋111×12， ∴x －22－7－x 4≤13－14＋14－15＋…＋111－112， ∴x －22－7－x 4≤13－112， ∴x －22－7－x 4≤14， 解得x≤4，∴原不等式的解集是x≤4，在数轴上表示如下所示，【培优训练】19．解：(1)由分母为－x 2＋1，可设－x 4－6x 2＋8＝(－x 2＋1)(x 2＋a)＋b ，则－x 4－6x 2＋8＝(－x 2＋1)(x 2＋a)＋b ＝－x 4－ax 2＋x 2＋a ＋b ＝－x 4－(a －1)x 2＋(a ＋b)． ∵对于任意x ，上述等式均成立，∴⎩⎪⎨⎪⎧a －1＝6，a ＋b ＝8，∴⎩⎪⎨⎪⎧a ＝7，b ＝1. ∴－x 4－6x 2＋8－x 2＋1＝（－x 2＋1）（x 2＋7）＋1－x 2＋1＝（－x 2＋1）（x 2＋7）－x 2＋1＋1－x 2＋1 ＝x 2＋7＋1－x 2＋1.这样，分式－x 4－6x 2＋8－x 2＋1被拆分成了一个整式x 2＋7与一个分式1－x 2＋1的和． (2)由－x 4－6x 2＋8－x 2＋1＝x 2＋7＋1－x 2＋1知， 对于x 2＋7＋1－x 2＋1，当x ＝0时，这两个式子的和有最小值，最小值为8，即－x 4－6x 2＋8－x 2＋1的最小值为8. 20．解：∵a≠0，xx 2＋x ＋1＝a ，∴x 2＋x ＋1x ＝1a ，即x ＋1x ＝1a －1∵x 4＋x 2＋1x 2＝x 2＋1＋1x 2＝(x ＋1x )2－1 ＝(1a －1)2－1＝1a 2－2a ＝a －2a 2 ∴x 2x 4＋x 2＋1＝a 2a －2.第六节 数的开方与二次根式姓名：________ 班级：________ 用时：______分钟1. (2018·辽宁抚顺中考)二次根式1－x 在实数范围内有意义，则x 的取值范围是( ) A ．x≥1B ．x≤1C ．x ＞1D ．x ＜12．(2018·浙江杭州中考)下列计算正确的是( )A.22＝2 B.22＝±2 C.42＝2D.42＝±23．(2018·云南曲靖中考)下列二次根式中能与23合并的是( ) A.8 B.13C.18D.94．(2018·江苏泰州中考)下列运算正确的是( ) A.2＋3＝ 5 B.18＝2 3 C.2·3＝ 5D.2÷12＝2 5．(2018·重庆中考A 卷)估计(230－24)·16的值应在( ) A ．1和2之间 B ．2和3之间 C ．3和4之间D ．4和5之间6．式子x －2x －3有意义的条件是__________________．7．(2018·山东潍坊中考)用教材中的计算器进行计算，开机后依次按下，把显示结果输入右侧的程序中，则输出的结果是______.8．(2018·广东广州中考)如图，数轴上点A 表示的数为a ，化简：a ＋a 2－4a ＋4＝______．9．(2017·四川德阳中考)计算：(25－2)0＋|2－5|＋(－1)2 017－13×45.10．(2018·浙江台州模拟)已知x ＝2－1，求x 2＋3x －1的值．11．已知y ＝2x －5＋5－2x －3，则2xy 的值为( )A ．－15B ．15C ．－152D.15212．如果一个三角形的三边长分别为1，k ，4，那么化简|2k －5|－k 2－12k ＋36的结果是( ) A ．3k －11 B ．k ＋1 C ．1D ．11－3k13．已知a ，b 分别是6－13的整数部分和小数部分，那么2a －b 的值是( ) A ．3－13 B ．4－13 C.13D ．2＋1314．若关于x 的方程－2x ＋m 2 017－x ＋4 020＝0存在整数解，则正整数m 的所有取值的和为________. 15．已知|a －2 017|＋a －2 018＝a ，则a －2 0172的值是______________． 16．已知a ＝1－3，b ＝1＋3，求2a 2＋2b 2－3ab －a ＋b 的值．17．请在方格内画△ABC，使它的顶点都在格点上，且三边长分别为2，25，412. (1)求△ABC 的面积； (2)求出最长边上的高．18．(2019·创新题)小明在学习《二次根式》后，发现一些含根号的式子可以写成另一个式子的平方，如3＋22＝(1＋2)2.善于思考的小明进行了以下探索：设a＋b2＝(m＋n2)2(其中a，b，m，n均为整数)，则有a＋b2＝m2＋2n2＋2mn 2.∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把类似a＋2b的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：(1)当a，b，m，n均为正整数时，若a＋b3＝(m＋n3)2，用含m，n的式子分别表示a，b，得a＝________，b＝________；(2)利用所探索的结论，找一组正整数a，b，m，n填空：________＋________3＝(________＋________3)2；(3)若a＋43＝(m＋n3)2，且a，m，n均为正整数，求a的值．19．阅读下列材料，回答有关问题：在实数这章中，遇到过2，3，9，12，a这样的式子，我们把这样的式子叫做二次根式，根号下的数叫做被开方数．如果一个二次根式的被开方数中有的因数能开得尽方，可以利用a·b＝a·b(a≥0，b≥0)；ab＝ab(a≥0，b>0)将这些因数开出来，从而将二次根式化简．当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时，这样的二次根式叫做最简二次根式，例如，1 3化成最简二次根式是33，27化成最简二次根式是33，几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式叫做同类二次根式，如上面的例子中的13和27就是同类二次根式．(1)请判断下列各式中，哪些是同类二次根式？2，75，18，150，127， 3.(2)二次根式中的同类二次根式可以像整式中的同类项一样合并，请计算：2＋75－18－150＋127－ 3.20．在进行二次根式化简时，我们有时会碰上如53，23，23＋1一样的式子，其实我们还可以将其进一步化简：53＝5×33×3＝533，23＝2×33×3＝63，23＋1＝2×（3－1）（3＋1）＝2（3－1）（3）2－12＝3－1，23＋1还可以用以下方法化简：23＋1＝3－13＋1＝（3）2－123＋1＝（3＋1）（3－1）3＋1＝3－1. 以上这种化简的方法叫做分母有理化． (1)请化简25＋3＝________；(2)若a 是2的小数部分则3a＝________；(3)矩形的面积为35＋1，一边长为5－2，则它的周长为________； (4)化简21＋5＋25＋9＋29＋13＋…＋24n －3＋4n ＋1.参考答案【基础训练】1．B 2.A 3.B 4.D 5.B 6．x≥2且x≠3 7.7 8.29．解：原式＝1＋5－2－1－5＝－2. 10．解：∵x＝2－1，∴x＋1＝2， ∴(x＋1)2＝(2)2＝2， 即x 2＋2x ＋1＝2， ∴x 2＋2x ＝1，∴x 2＋3x －1＝x 2＋2x ＋x －1＝1＋x －1＝2－1. 【拔高训练】11．A 12.A 13.C 14.15 15.2 018 16．解：∵a＝1－3，b ＝1＋3， ∴a－b ＝(1－3)－(1＋3)＝－23， ab ＝(1－3)(1＋3)＝－2，∴2a 2＋2b 2－3ab －a ＋b ＝2(a －b)2－(a －b)＋ab ＝2(－23)2－(－23)＋(－2) ＝22＋2 3.17．解：画图如图所示．(1)S △ABC ＝2.(2)最长边上的高为255.18．解：(1)∵a＋b 3＝(m ＋n 3)2， ∴a＋b 3＝m 2＋3n 2＋2mn 3， ∴a＝m 2＋3n 2，b ＝2mn.(2)答案不唯一，如：设m ＝1，n ＝1， ∴a＝m 2＋3n 2＝4，b ＝2mn ＝2. (3)由题意，得： a ＝m 2＋3n 2，b ＝2mn∵4＝2mn ，且m ，n 为正整数， ∴m＝2，n ＝1或m ＝1，n ＝2，∴a＝22＋3×12＝7或a ＝12＋3×22＝13. 19．解：(1)75＝53，18＝32，150＝210，127＝39， ∴2，18，150是同类二次根式；75，127，3是同类二次根式． (2)原式＝2＋53－32－210＋39－3＝－21210＋3739. 【培优训练】 20．解：(1)5－ 3 (2)32＋3 (3)30＋16 5(4)原式＝2（5－1）5－1＋2（9－5）9－5＋2（13－9）13－9＋…＋2（4n ＋1－4n －3）（4n ＋1）－（4n －3）＝5－1＋9－5＋13－9＋…＋4n ＋1－4n －32＝4n ＋1－12.。

只有你学会把自己已有的成绩都归零，才能腾出空间去接纳更多的新东西，如此才能使自己不断的超越自己。

无论你觉得自己多么的了不起，也永远有人比你更强；无论你觉得自己多么的不幸，永远有人比你更加不幸。

数的开方与二次根式
课前诊断测试
1．(2018·甘肃兰州中考)下列二次根式中，是最简二次根式的是( ) A.18 B.13 C.27 D.12
2. (2018·江苏无锡中考)下列等式正确的是( )
A ．(3)2＝3
B.（－3）2＝－3
C.33＝3
D ．(－3)2＝－3 3．(2018·四川达州中考)二次根式2x ＋4中x 的取值范围是( )
A ．x ＜－2
B ．x≤－2
C ．x ＞－2
D ．x≥－2
4．(2018·福建中考)已知m ＝4＋3，则以下对m 的估算正确的是( )
A ．2<m<3
B ．3<m<4
C ．x>－2
D ．x≥－2
5．(2018·湖南益阳中考)12×3＝______．
6. (2018·甘肃白银中考)使得代数式1
x －3有意义的x 的取值范围是__________． 7．(2018·天津中考)计算(6＋3)(6－3)的结果等于______. 8．(2018·山东烟台中考)12与最简二次根式5a ＋1是同类二次根式，则a ＝______． 9. (2018·广东东莞中考)已知a －b ＋|b －1|＝0，则a ＋1＝______.
参考答案
1．B 2.A 3.D 4.B
5．6 6.x>3 7.3 8.2 9.2。