2018-2019学年上海市虹口区上外初一下期末考数学试卷(有答案)

七年级下学期期末数学试卷一、选择题（每题只有一个答案正确）1．不等式组的解集是（）A．B．C．D．【答案】D【解析】根据不等式解集的确定方法，大小，小大中间找，即可得出解集．【详解】∵∴解集为：.故选D.【点睛】此题主要考查了不等式组的解集确定方法，得出不等式解集确定方法是解题关键．2．有四条线段，长度分别是4，6，8，10，从中任取三条能构成直角三角形的概率是（）A．13B．14C．12D．34【答案】B【解析】从四条线段中任意选取三条，找出所有的可能，以及能构成直角三角形的情况数，即可求出所求的概率．【详解】从四条线段中任意选取三条，所有的可能有：4，6，8；4，6，10；6，8，10；4，8，10共4种，其中构成直角三角形的有6，8，10共1种，则P（构成直角三角形）=1 4故选B．【点睛】从四条线段中任意选取三条，找出所有的可能，以及能构成直角三角形的情况数，即可求出所求的概率．3．若12xy=⎧⎨=-⎩是关于x和y的二元一次方程1ax y+=的解，则a的值等于（）A．3 B．1 C．1-D．3-【答案】A【解析】将方程的解代入所给方程，再解关于a的一元一次方程即可．【详解】解：将12xy=⎧⎨=-⎩代入1ax y+=得，21a-=，a ．解得：3故选：A．【点睛】本题考查的知识点是二元一次方程的解以及解一元一次方程，比较基础，难度不大．4．有一种手持烟花，点然后每隔1.4秒发射一发花弹。

要求每一发花弹爆炸时的高度要超过15米，否则视为不合格，在一次测试实验中，该烟花发射出的第一发花弹的飞行高度（米）随飞行时间（秒）变化的规律如下表所示.下列这一变化过程中说法正确的是（）A．飞行时间t每增加0.5秒，飞行高度h就增加5.5米B．飞行时间t每增加0.5秒，飞行高度h就减少5.5米C．估计飞行时间t为5秒时，飞行高度h为11.8米D．只要飞行时间t超过1.5秒后该花弹爆炸，就视为合格【答案】C【解析】根据表格观察规律即可求解.【详解】通过表格的整体观察可以直接排除A，B，要求每一发花弹炸时的高度要超过15米，排除D.故选C.【点睛】本题主要考查观察表格发现规律，仔细观察是解题关键.5．如图，小米同学把一个含45°角的直角三角板放在如图所示的两条平行线m，n上，经测量∠α=115°，则∠β的度数是（）A．55°B．65°C．75°D．70°【答案】D【解析】分析：根据邻补角的性质、三角形的内角和等于180°、两直线平行，同位角相等、对顶角相等可求得∠β=70°.详解：如图所示：∵∠α=115°，∠α=∠A+∠AED，∴∠AED=∠α-∠A=115°-45°=70°.∵m∥n,∴∠AFG=∠AED=70°.∴∠β=∠AFG=70°.故选D.点睛：本题考查了三角形的外角的性质，平行线的性质，对顶角的性质等知识点，灵活运用知识是解决问题的关键.6．下列实数中的无理数是（）A．1.414B．0C．﹣13D．2【答案】D【解析】无理数就是无限不循环小数，理解无理数的概念，同时也要理解有理数的概念，有理数是整数与分数的统称，即有限小数和无限循环小数是有理数，而无限不循环小数是无理数，由此即可判定选项. 【详解】A、由于1.414为有限小数，它是有理数；B、0是整数，它是有理数；C、13-是无限循环小数，它是有理数；D、2是无限不循环小数，它是无理数.故选：D.【点睛】此题主要考查了无理数的定义.初中范围内学习的无理数有：π、2π等；开方开不尽的数；以及像0.1010010001...，等有这样规律的数.7．如图，把矩形ABCD沿EF对折后使两部分重合，若150∠=，则AEF∠=（）A ．110°B ．115°C ．120°D ．130°【答案】B 【解析】根据翻折的性质可得∠2=∠3，再求出∠3，然后根据两直线平行，同旁内角互补列式计算即可得解．【详解】∵矩形ABCD 沿EF 对折后两部分重合，150∠=，∴∠3=∠2=180-502︒︒=65°， ∵矩形对边AD∥BC，∴∠AEF=180°-∠3=180°-65°=115°．故选：B ．【点睛】本题考查了矩形中翻折的性质，两直线平行的性质，平角的定义，掌握翻折的性质是解题的关键．8．用代入法解方程组23328y x x y ①②=-⎧⎨+=⎩时，将方程①代入②中，所得的方程正确的是( ). A ．3x ＋4y －3=8B ．3x ＋4x －6=8C ．3x －2x －3=8D ．3x ＋2x －6=8【答案】B【解析】把①代入②得，3x+2（2x-3）=8，整理后即可得答案.【详解】把①代入②得，3x+2（2x-3）=8，整理得，3x+4x-6=8，故选B ．【点睛】本题考查了代入法解二元一次方程组，熟练掌握代入法是解题的关键.9．下列各式中，与()2a 1?－相等的是（ ） A ．2a 1-B ．2a 2a 1-+C ．2a 2a 1--D ．2a 1+ 【答案】B【解析】根据完全平方公式求出（a-1）1=a 1-1a+1，即可选出答案．【详解】∵（a-1）1=a 1-1a+1，∴与（a-1）1相等的是B ，故选：B．【点睛】本题考查了运用完全平方公式进行计算，注意：（a-b）1=a1-1ab+b1．10．下列运算正确的等式是（）A．(5-m)(5+m)=m2-25 B．(1-3m)(1+3m)=1-3m2C．(-4-3n)(-4+3n)= -9n2+16 D．(2ab-n)(2ab+n)=4ab2-n2【答案】C【解析】解：A．（5-m）（5+m）= 25-m2，所以此选项是错误的；B．（1-3m）（1+3m）=1-9m2，所以此选项是错误的；C．（-4-3n）（-4+3n）= -9n2+16，此选项是正确；D．（2ab-n）（2ab+n）=4a2b2-n2，所以此选项是错误的；故选C．二、填空题题11．数学课上，老师请同学们思考如下问题：小军同学的画法如下：老师说，小军的画法正确.请回答：小军画图的依据是：________.【答案】在同一平面内，过一点有且只有一条直线与已知直线垂直；垂直定义；同位角相等，两直线平行【解析】分析：在同一平面内，过一点有且只有一条直线与已知直线垂直；垂直定义等即可解决问题.详解：在同一平面内，过一点有且只有一条直线与已知直线垂直；垂直定义；同位角相等，两直线平行.故答案为在同一平面内，过一点有且只有一条直线与已知直线垂直；垂直定义；同位角相等，两直线平行. 点睛：本题考查作图-基本作图，在同一平面内，过一点有且只有一条直线与已知直线垂直；垂直定义；同位角相等，两直线平行，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．12．在平面直角坐标系的第二象限内有一点M ，点M 到x 轴的距离为4，到y 轴的距离为3，则点M 的坐标是______.【答案】()3,4【解析】根据点到x 轴的距离是纵坐标的绝对值，点到y 轴的距离是点的横坐标的绝对值，第二象限内点的横坐标小于零，纵坐标大于零，可得答案．【详解】由点且到x 轴的距离为4、到y 轴的距离为3，得|y|=4，|x|=3.由M 是第二象限的点，得x=−3，y=4.即点M 的坐标是（−3，4)，故答案为：（−3，4)【点睛】此题考查象限及点的坐标的有关性质，解题关键在于第二象限内点的横坐标小于零，纵坐标大于零 13．如图已知∠ABC=∠DEF，BE=FC,要证明△ABC≌△DEF,若以“ASA”为依据，还需要添加的条件__________.【答案】或【解析】要使△ABC ≌△DEF ，已知∠ABC=∠DEF ，BE=FC ，由BE=FC 可得BE+BC=FC+BC ，即BC=EF ，具备了一组角和一组边对应相等，还缺少角对应相等的条件，直接给出或结合判定方法得出即可． 【详解】补充条件为：或，理由：∵ BE=FC ，∴BE+BC=FC+BC ，即BC=EF ， 又∵， ∴（两直线平行同位角相等） 在△ABC 和△DEF 中，∴△ABC ≌△DEF(ASA)故答案为：或【点睛】本题考查全等三角形的判定，掌握ASA判定定理是关键.14．如图，△ABC 的外角平分线AM 与边BC 平行，则∠B_____∠C（填“＞”，“=”，或“＜”）．【答案】＝【解析】依据AM∥BC，即可得到∠DAM＝∠B，∠CAM＝∠C，再根据AM平分∠DAC，即可得到∠DAM ＝∠CAM，进而得出∠B＝∠C．【详解】解：如图，∵AM∥BC，∴∠DAM＝∠B，∠CAM＝∠C，∵AM平分∠DAC，∴∠DAM＝∠CAM，∴∠B＝∠C．故答案为：＝．【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等；两直线平行，内错角相等．15．已知∠α和∠β互为补角，且∠β比∠α小30°，则∠β等于____°【答案】75°．【解析】根据题目中的等量关系列方程组求解即可.【详解】∵∠α和∠β互为补角，且∠β比∠α小30°，∴18030αββα∠+∠=︒⎧⎨∠=∠-︒⎩，解得：∠α＝105°，∠β＝75°，故答案为：75°．【点睛】本题考查补角的定义以及二元一次方程组的应用，根据题意列出方程组是解题关键.16．等腰三角形是轴对称图形，__________是它的对称轴．【答案】顶角平分线、底边上的中线、底边上的高所在直线（答案不唯一）【解析】分析：根据轴对称图形的概念识别和等腰三角性质的性质回答即可.详解：∵等腰三角形的顶角平分线在边上的中线、底边上的高相应重合，又∵等腰三角形是轴对称图形，∴其对称轴是顶角平分线，底边上的中线、底边上的高线所在直线．故答案为顶角平分线，底边上的中线、底边上的高线所在直线.（答案不唯一，写出其中任意一个即可） 点睛：此题主要考查了等腰三角形的性质，等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴.17．若三角形三条边长分别是1，a ，5(其中a 为整数)，则a 的取值为______．【答案】1【解析】∵三角形的两边长分别为1和1，∴第三边长a 的取值范围是：1-1<a<1+1，即：4<a<6，∴a 的值为1，故答案为1．三、解答题18．解下列方程组.(1)34194x y x y +=⎧⎨-=⎩(2)212350x y x y +=⎧⎨++=⎩ 【答案】（1）51x y =⎧⎨=⎩ （2）23x y =⎧⎨=-⎩【解析】(1) 通过观察未知数y 的系数，可以通过把第二式扩大4倍之后，与第一式相加消掉未知数y ，得到x 的值，然后用代入法把x 的值代入第二式，解得y 的值.(2) 首先把第一，二式的格式统一，把第二式5移项到等式右边，再因为x 的系数一样，用减法消掉x ，得到y ，然后用代入法把y 的值代入第一式得到x 的值.【详解】（1）3419,4x y x y +=⎧⎨-=⎩①，② 解：②×4，得4416x y -= ③①+③ 得735x = 解得5x =把5x =代入②，得54y -=解得：1y =所以原方程组的解是51x y =⎧⎨=⎩（2）21,2350x y x y +=⎧⎨++=⎩①，② 解：由②得235x y +=- ③③-①得26y =-解得3y =-把3y =-代入①得231x -=解得2x =所以原方程组的解是23x y =⎧⎨=-⎩ 【点睛】本题考查了二元一次方程组的解法，对于二元一次方程的题，通过观察未知数的系数来选择合适的解题方法，①当某一个未知数系数相同或互为相反数，可以用加减消元法解题.②当某一个未知数系数为1时，可以选择代入消元法解题.③当未知数关系不能直接判断时，可通过扩大或缩小未知数的系数，来选择合适的消元方法. 19．（1）解方程组：2112x y x y +=⎧⎨-=-⎩；（2）解下列不等式2134136x x ---≤. 【答案】（1）3x =，5y =；（2）4x .【解析】（1）用加减法消去未知数y 求出x 的值，再代入求出y 的值即可；（2）根据解一元一次不等式的步骤，去分母、去括号、移项、合并同类项、系数化为1，即可得出结果.【详解】（1）211{2x y x y +--＝①＝②，①+②得，3x=9，解得x=3，把x=3代入②得，y=5，∴原方程组的解为：3{5x y ＝＝．（2）∵2134136x x ---≤ ∴2（2x-1）-6≤3x -1∴1x-2-6≤3x -1∴1x-3x≤-1+2+6∴x≤1∴不等式组的解集为x≤1．【点睛】此题考查了二元一次方程组的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键． 20．一个运输公司有甲、乙两种货车，两次满载的运输情况如下表：（1）求甲、乙两种货车每次满载分别能运输多少吨货物；（2）现有一批重34吨的货物需要运输，而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输，为了使保养费用不超过700元，公司该如何安排甲、乙两种货车来完成这次运输任务.【答案】（1）4吨，2.5吨 （2）甲车6辆，乙车4辆或甲车7辆，乙车3辆【解析】（1）设甲车每辆运输x 吨，乙车每辆运输y 吨，再根据统计图中的数据列出方程组即可解答. （2）设安排甲车a 辆，则乙车（10-a ）辆，再根据有一批重34吨的货物需要运输，而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输，为了使保养费用不超过700元，列出不等式组即可解答.【详解】解：（1）解，设甲车每辆运输x 吨，乙车每辆运输y 吨24185635x y x y +=⎧⎨+=⎩解得42.5x y =⎧⎨=⎩ 答：甲车每辆运输4吨，乙车每辆运输2.5吨（2）解，设安排甲车a 辆，则乙车（10-a ）辆4 2.5(10)348040(10)700a a a a +-≥⎧⎨+-≤⎩解得67.5a ≤≤∵a 是整数∴a 可以取的整数是6，7答：公司可以安排甲车6辆，乙车4辆或甲车7辆，乙车3辆【点睛】此题考查二元一次方程组的应用，一元一次不等式组的应用，解题关键在于列出方程.21．为提高学生综合素质，亲近自然，励志青春，某学校组织学生举行“远足研学”活动，先以每小时6千米的速度走平路，后又以每小时3千米的速度上坡，共用了3小时；原路返回时，以每小时5千米的速度下坡，又以每小时4千米的速度走平路，共用了4小时，问平路和坡路各有多远. 【答案】平路有443千米，坡路有53千米【解析】设去时平路为xkm ，上山的坡路为ykm ，根据去的时候共用3h ，返回时共用4h ，列方程组即可．【详解】解：设平路有x 千米，坡路有y 千米.由题意可知 363445x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ 解得44353x y ⎧=⎪⎪⎨⎪=⎪⎩答：平路有443千米，坡路有53千米 【点睛】本题考查了由实际问题抽象出二元一次方程组，解答本题的关键是读懂题意，找出合适的等量关系，列方程组．22．如图，//EF BC ，1B ∠=∠，2180BAD ∠+∠=.说明：3G ∠=∠.请完成如下解答.解：因为//EF BC （已知）所以12∠=∠（ ）因为1B ∠=∠（已知）所以2B ∠=∠（ ）所以//AB （ ）所以BAD D ∠+∠= （ ）因为2180BAD ∠+∠=（已知）所以D 2∠=∠（ ）所以//AD （ ）所以3G ∠=∠（ ）【答案】见解析.【解析】先依据平行线的性质得出∠1=∠2，进而判定AB ∥CD ，再根据平行线的性质得出∠BAD+∠D=180°，进而判定AD ∥BG ，即可得出结论．【详解】因为EF ∥BC(已知)所以∠1=∠2(两直线平行,内错角相等).因为∠B=∠1(已知)所以∠B=∠2(等量代换).所以AB ∥CD.（同位角相等，两直线平行）所以∠BAD+∠D=180°. （两直线平行，同旁内角互补）因为∠BAD+∠2=180°(已知)所以∠D=∠2(等量代换).所以AD ∥BG. （内错角相等，两直线平行）所以∠3=∠G(两直线平行,内错角相等).故答案为：两直线平行，内错角相等；等量代换；CD ；同位角相等，两直线平行；180；两直线平行，同旁内角互补；等角的补角相等（或等量代换）；BG ；内错角相等，两直线平行； 两直线平行，内错角相等.【点睛】此题考查平行线的性质，解题关键在于熟练掌握和灵活运用平行线的判定定理与性质定理.23．先化简，再求值：3x 1+(1x 1-3x)-(x+5x 1)，其中x=1．【答案】-4x ，-8【解析】先去括号合并同类项，然后把x=1代入计算即可.【详解】原式=3x 1+(1x 1-3x)-(x+5x 1)=3x 1＋1x 1－3x －x －5x 1=－4x ，当x =1时，原式 =-4×1= －8.【点睛】本题考查了整式的化简求值，解答本题的关键是熟练掌握整式的运算法则，将所给多项式化简.本题主要利用去括号合并同类项的知识，注意去括号时，如果括号前是负号，那么括号中的每一项都要变号；合并同类项时，只把系数相加减，字母与字母的指数不变.24． (1)计算：322-+⎭；(2)解方程组：22345x y x y ⎧+=⎪⎨⎪-=⎩.【答案】；(2)23x y =⎧⎨=⎩. 【解析】（1）根据实数的运算法则进行运算，即可得出结论；（2）将原方程组进行化简，化简后用加减消元法求解即可得出结论.【详解】解：(1)原式＝322=+⎭13222⎛=--+ ⎝=1；(2)方程组整理得：321245x y x y +=⎧⎨-=⎩①②， ①+②×2得：11x ＝22，解得：x ＝2，把x ＝2代入①得：6+2y ＝12，解得：y ＝3，则方程组的解为23x y =⎧⎨=⎩． 【点睛】此题考查了实数运算和解二元一次方程组，解方程组利用了消元的思想，消元的方法有：代入消元法与加减消元法．25．已知，平面直角坐标系内，点A （a ，0），B （b ，2），C （0，2），且a 、b 是方程组213211a b a b +=⎧⎨+=⎩的解，求：（1）a 、b 的值．（2）过点E （6，0）作PE∥y 轴，点Q （6，m ）是直线PE 上一动点，连QA 、QB ，试用含有m 的式子表示△ABQ 的面积．（3）在（2）的条件下．当△ABQ的面积是梯形OABC面积一半时，求Q点坐标．【答案】(1)a=5,b=3;(2) △ABQ的面积为|m+1|；(3) Q（6，3）或（6，﹣5）．【解析】（1）解方程组可直接求出a、b的值；（2）先求出直线AB的解析式为y=﹣x+5，当点Q在AB上时，m=﹣1，然后分当m＞﹣1时和m＜﹣1时两种情况求解；（3）计算S梯形OABC，根据△ABQ的面积是梯形OABC面积一半列出方程求m的值即可．【详解】（1）由方程组两式相加，得a+b=8，再与方程组中两式分别相减，得；（2）由（1）可知，A（5，0），B（3，2），∴直线AB的解析式为y=﹣x+5，当点Q在AB上时，m=﹣1，如图1，当m＞﹣1时，过B点作BD⊥x轴，垂足为D，则S△ABQ=S梯形BDEQ﹣S△ABD﹣S△AQE=（2+m）×（6﹣3）﹣×2×（5﹣3）﹣×（6﹣5）×m=m+1；当m＜﹣1时，如图2所示，过点B作BM⊥EQ于点M，则S△ABQ=S△BMQ﹣S△AEQ﹣S梯形AEMB=×（2﹣m）×（6﹣3）﹣×（6﹣5）×（﹣m）﹣×（6﹣3+6﹣5）×2=3﹣m+m﹣4=﹣m﹣1．综上所述，△ABQ的面积为|m+1|；（3）∵S梯形OABC=×（3+5）×2=8，依题意，得|m+1|=×8，解得m=3或m=﹣5；∴Q（6，3）或（6，﹣5）．【点睛】本题考查了解二元一次方程组，待定系数法求一次函数解析式，坐标与图形的性质，三角形、梯形的面积计算及分类讨论的数学思想．关键是根据题意画出图形，结合图形上点的坐标表示相应的线段长．七年级下学期期末数学试卷一、选择题（每题只有一个答案正确）1．观察下列等式:① 32 - 12 = 2 × 4② 52 - 32 = 2 × 8③ 72 - 52 = 2 × 12......那么第n （n 为正整数）个等式为A ．n 2 - (n-2)2 = 2 × (2n-2)B ．(n+1)2 - (n-1)2 = 2 × 2nC ．(2n)2 - (2n-2)2 = 2 ×(4n -2)D ．(2n+1)2 - (2n-1)2 = 2 × 4n 【答案】D【解析】分析：观察分析所给等式，找到其中的规律即可得到结论.详解：观察、分析所给等式可知：第n 个等式的左边是两个连续奇数(21)n +和(21)n -的平方差，右边是2与4n 的积，由此可得：第n 个等式为：22(21)(21)24n n n +--=⨯.故选D.点睛：分析、观察得到每个等式的左边和右边的式子与序号n 间的关系是解答本题的关键. 2．已知三角形的一边长是(x+3)cm ，该边上的高是5 cm ，它的面积不大于20 cm 2，则( ) A ．x>5B ．－3<x≤5C ．x≥－3D ．x≤5 【答案】B 【解析】由题意可得：15(3)202x ⨯+≤且30x +> 解得：5x ≤且3x >-，∴35x -<≤.故选B.3．下列各组线段不能组成三角形的是（ ）A ．3cm ，8cm ，5cmB ．6cm ，6cm ，6cmC ．3cm ，5cm ，7cmD ．3cm ，4cm ，5cm【答案】A【解析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边列出不等式即可．【详解】根据三角形的三边关系，A、3+5=8，不能组成三角形；B、6+6＞6，能组成三角形；C、3+5＞7，能组成三角形；D、3+4＞5，能组成三角形；故选：A．【点睛】本题考查的是三角形的三边关系，掌握三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．4．若x＜y，比较2-3x与2-3y的大小，则下列式子正确的是（）A．2-3x＞2-3y B．2-3x＜2-3y C．2-3x=2-3y D．无法比较大小【答案】A【解析】根据不等式的基本性质对以下选项进行一一验证即可．【详解】解：在不等式x＜y的两边同时乘以-3，不等号的方向改变，即-3x＞-3y．在不等式-3x＞-3y的两边同时加上2，不等号的方向不变，即2-3x＞2-3y，故选项A正确．故选：A．【点睛】主要考查了不等式的基本性质．不等式的基本性质：（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变．（2）不等式两边乘（或除以）同一个正数，不等号的方向不变．（3）不等式两边乘（或除以）同一个负数，不等号的方向改变．5．小明到商店购买“五四青年节”活动奖品，购买20只铅笔和10本笔记本共需110元，但购买30支铅笔和5本笔记本只需85元，设每支铅笔x元，每本笔记本y元，则可列方程组（）A．203011010585x yx y+=⎧⎨+=⎩B．201011030585x yx y+=⎧⎨+=⎩C．205110301085x yx y+=⎧⎨+=⎩D．520110103085x yx y+=⎧⎨+=⎩【答案】B【解析】解：设每支铅笔x元，每本笔记本y元，根据题意得：201011030585x yx y+=⎧⎨+=⎩．故选B．点睛：本题考查了由实际问题抽象出二元一次方程组，根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．6）A．3与4之间B．5与6之间C．6与7之间D．3与10之间【答案】B【解析】直接利用估算无理数的方法得出接近无理数的整数进而得出答案．【详解】解：∵25<30<36，25∴＜30＜36，即：5＜30＜6，∴30的值在5与6之间．故选B．【点睛】此题主要考查了估算无理数的大小，正确掌握二次根式的性质是解题关键．7．十一旅游黄金周期间，某景点举办优惠活动，成人票和儿童票均有较大折扣，王明家去了3个大人和4个小孩，共花了400元，李娜家去了4个大人和2个小孩，共花了400元，王斌家计划去3个大人和2个小孩，请你帮助他算一下，需要准备多少门票钱？（）A．300元B．310元C．320元D．330元【答案】C【解析】试题解析：设大人门票为x，小孩门票为y，由题意,得：34400 42400 x yx y，+=⎧⎨+=⎩解得：8040 xy=⎧⎨=⎩，则3x+2y=320.即王斌家计划去3个大人和2个小孩，需要320元的门票.故选C.8．下列某不等式组的解集在数轴上表示如图所示，则该不等式组是（）A．1313xx-<⎧⎨+<⎩B．1313xx-<⎧⎨+>⎩C．1313xx->⎧⎨+>⎩D．1313xx->⎧⎨+<⎩【答案】B【解析】分析：先根据在数轴上表示不等式解集的方法得出该不等式组的解集，再找出符合条件的不等式组即可．详解：A、此不等式组的解集为x＜2，不符合题意；B、此不等式组的解集为2＜x＜4，符合题意；C 、此不等式组的解集为x ＞4，不符合题意；D 、此不等式组的无解，不符合题意；故选：B ．点睛：本题考查的是在数轴上表示不等式的解集，解答此类题目时一定要注意实心与空心圆点的区别，即一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心，若边界点含于解集为实心点，不含于解集即为空心点．9．下列各数中是无理数的是（ ）A ．3B ．4C ．38D ．3.14 【答案】A【解析】根据无理数的定义（无理数是指无限不循环小数）进行判断即可．【详解】A.3是无理数，故本选项正确； B.4=2不是无理数，是有理数，故本选项错误； C. 38=2，是有理数，不是无理数，故本选项错误；D. 3.14不是无理数，故本选项错误；故选A【点睛】此题考查无理数，难度不大10．下列运算正确的是（ ）A ．3a +2a ＝5a 2B ．2a 2b ﹣a 2b ＝a 2bC ．3a +3b ＝3abD ．a 5﹣a 2＝a 3 【答案】B【解析】根据合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，判断即可.【详解】A 、325a a a += ，故本选项错误；B 、222 2a b a b a b ﹣＝ ，故本选项正确；C 、3a 与3b 不是同类项，不能合并，故本选项错误；D 、a 5与a 2不是同类项，不能合并，故本选项错误．故选B ．【点睛】本题考查了合并同类项，正确理解同类项的意义是解题的关键．二、填空题题11．如图，在五边形ABCDE 中，，DP 、CP 分别平分EDC 、BCD ，则的大小为____度．【答案】1【解析】根据五边形的内角和等于540°，由∠A+∠B+∠E=300°，可求∠BCD+∠CDE的度数，再根据角平分线的定义可得∠PDC与∠PCD的角度和，进一步求得∠P的度数．【详解】∵五边形的内角和等于540°，∠A+∠B+∠E=300°，∴∠BCD+∠CDE=540°-300°=240°，∵∠BCD、∠CDE的平分线在五边形内相交于点P，∴∠PDC+∠PCD=（∠BCD+∠CDE）=120°，∴∠P=180°-120°=1°．故答案为：1．【点睛】本题主要考查了多边形的内角和公式，角平分线的定义，熟记公式是解题的关键．注意整体思想的运用．12．将点P（﹣2，0）向左平移2个单位得点P′，则点P′的坐标是___．【答案】(-4,0)【解析】直接利用平移中点的变化规律求解即可．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．【详解】将点P（﹣2，0）向左平移2个单位得点P′，则点P′的坐标是（﹣2-2，0）故答案为：(-4,0)【点睛】此题考查坐标与图形变化-平移，解题关键在于掌握平移性质.13．已知等边三角形ABC的高为6，在这个三角形所在的平面内有一个点P，若点P到AB的距离是1，点P到AC的距离是2，则点P到BC的最小距离与最大距离分别是_______.【答案】3和1【解析】根据题意画出相应的图形，直线DM与直线NF都与AB的距离为1，直线NG与直线ME都与AC 的距离为2，当P与N重合时，HN为P到BC的最小距离；当P与M重合时，MQ为P到BC的最大距离，根据题意得到△NFG与△MDE都为等边三角形，利用锐角三角函数定义及特殊角的三角函数值求出DB与FB的长，以及CG与CE的长，进而由DB+BC+CE求出DE的长，由BC-BF-CG求出FG的长，求出等边三角形NFG与等边三角形MDE的高，即可确定出点P到BC的最小距离和最大距离．【详解】解：根据题意画出相应的图形，直线DM与直线NF都与AB的距离为1，直线NG与直线ME都与AC的距离为2，当P与N重合时，HN为P到BC的最小距离；当P与M重合时，MQ为P到BC的最大距离，根据题意得到△NFG与△MDE都为等边三角形，∵等边三角形ABC的高为6∴等边三角形ABC的边长：BC=3∴DB=FB23=，CE=CG43=，∴23+433=3FG=BC-BF-CG=234333-=∴NH=3，MQ=1则点P到BC的最小距离和最大距离分别是3，1．故答案为3，1．【点睛】此题考查了等边三角形的性质，以及平行线间的距离，作出相应的图形是解本题的关键．14．滴滴快车是一种便捷的出行工具，计价规则如下表：计费项目里程费时长费远途费单价 1.8元/公里0.3元/分钟0.8元/公里注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为：行车里程7公里以内（含7公里）不收远途费，超过7公里的，超出部分每公里收0.8元．小王与小张各自乘坐滴滴快车，行车里程分别为6公里与8.5公里．如果下车时两人所付车费相同，那么这两辆滴滴快车的行车时间相差_____分钟．【答案】1【解析】设小王的行车时间为x分钟，小张的行车时间为y分钟，根据题意列出小王和小张车费的代数式，两者相等，计算可得出时间差．【详解】解：设小王的行车时间为x 分钟，小张的行车时间为y 分钟，依题可得：1.8×6+0.3x=1.8×8.5+0.3y+0.8×（8.5-7），10.8+0.3x=16.5+0.3y ，0.3（x-y ）=5.7，x-y=1．故这两辆滴滴快车的行车时间相差1分钟．故答案为1．【点睛】本题考查二元一次方程的应用，解题的关键是仔细审题，确定已知量和未知量，找出它们之间的等量关系． 15．如图，已知AB DE ∥，80ABC ∠=︒，30BCD ∠=︒，则CDE ∠=_________.【答案】130【解析】根据两直线平行，内错角相等以及三角形外角的性质解答即可．【详解】反向延长DE 交BC 于M ．∵AB ∥DE ，∴∠BMD=∠ABC=80°，∴∠CMD=180°﹣∠BMD=100°；又∵∠CDE=∠CMD+∠BCD ，∴∠CDE=100°+30°=130°．故答案为：130°．【点睛】本题考查了平行线的性质，运用了平行线的性质、邻补角的关系、三角形的一个外角等于和它不相邻的两个内角和．16．如图，在方格纸中，以AB 为一边作ABP ∆，使之与ABC ∆全等，从1234,,,P P P P 四个点中找出符合条件的点P 的概率是__________．【答案】12．【解析】找到符合条件的点P的个数，再根据概率公式计算可得．【详解】解：要使△ABP与△ABC全等，点P的位置可以是P1，P2两个，∴从P1，P2，P3，P4四个点中找出符合条件的点P的概率是21 = 42故答案为：12．【点睛】本题主要考查概率公式的应用，随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数．17．已知二元一次方程4x+3y=9，若用含x 的代数式表示y，则有y=．【答案】3-43x【解析】先将与y无关的项移项，再把y的系数化为1即可．【详解】解：移项得，3y=9-4x，把y的系数化为1得，y=3-43 x．故答案为：3-4 3 x【点睛】本题考查的是解二元一次方程的变换，熟知解二元一次方程的基本步骤是解答此题的关键．三、解答题18．解不等式组523(1)13222x xx x+>-⎧⎪⎨≤-⎪⎩，并求出它的所有整数解的和．【答案】512x-<，-2【解析】先求出两个不等式的解集，再求其公共解，然后求出整数解的和即可．【详解】解：523(1) 13222x xx x+>-⎧⎪⎨-⎪⎩①②。

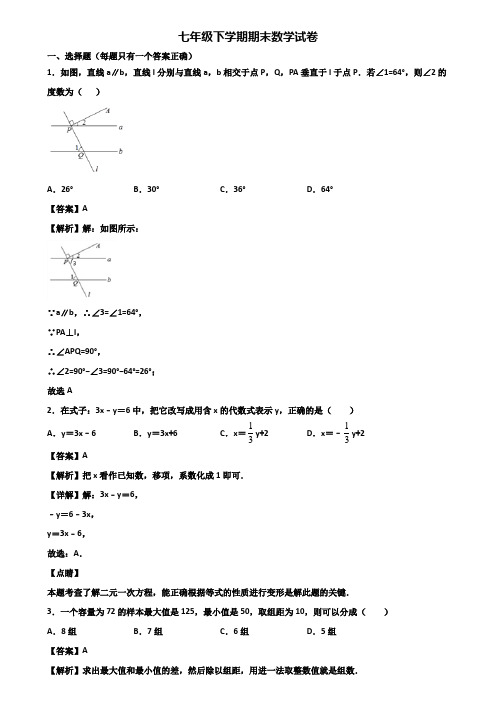
七年级下学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，直线a∥b，直线l分别与直线a，b相交于点P，Q，PA垂直于l于点P．若∠1=64°，则∠2的度数为（）A．26°B．30°C．36°D．64°【答案】A【解析】解：如图所示：∵a∥b，∴∠3=∠1=64°，∵PA⊥l，∴∠APQ=90°，∴∠2=90°−∠3=90°−64°=26°；故选A2．在式子：3x﹣y＝6中，把它改写成用含x的代数式表示y，正确的是（）A．y＝3x﹣6 B．y＝3x+6 C．x＝13y+2 D．x＝﹣13y+2【答案】A【解析】把x看作已知数，移项，系数化成1即可．【详解】解：3x﹣y＝6，﹣y＝6﹣3x，y＝3x﹣6，故选：A．【点睛】本题考查了解二元一次方程，能正确根据等式的性质进行变形是解此题的关键．3．一个容量为72的样本最大值是125，最小值是50，取组距为10，则可以分成（）A．8组B．7组C．6组D．5组【答案】A【解析】求出最大值和最小值的差，然后除以组距，用进一法取整数值就是组数．【详解】解：在样本数据中最大值为125，最小值是50，它们的差是125-50=75，已知组距为10，那么由于 75÷10=7. 5，故可以分成8组．故选：A ．【点睛】本题考查频率分布表中组数的确定，关键是求出最大值和最小值的差，然后除以组距，用进一法取整数值就是组数．4．若点（3+m ，n ﹣2）关于y 轴对称点的坐标是（3，2），则m ，n 的值为（ ）A ．m ＝﹣6，n ＝﹣4B ．m ＝0，n ＝4C ．m ＝﹣6，n ＝4D ．m ＝﹣6，n ＝0【答案】C【解析】根据关于y 轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变可得3+m+3＝0，n ﹣2＝2，再解即可．【详解】解：∵点（3+m ，n ﹣2）关于y 轴对称点的坐标是（3，2），∴3+m+3＝0，n ﹣2＝2，解得：m ＝﹣6，n ＝4，故选：C ．【点睛】此题主要考查了关于y 轴的对称点的坐标特点，关键是掌握点的坐标的变化规律．5．点P 是直线l 外一点，A 、B 、C 为直线l 上的三点，4PA cm =，5PB cm =，2PC cm =，则点P 到直线l 的距离（ ）A ．小于2cmB ．等于2cmC ．不大于2cmD ．等于4cm 【答案】C【解析】根据点到直线的距离是点到直线的垂线段的长度以及垂线段最短即可得答案．【详解】解：点P 为直线l 外一点，当P 点直线l 上的三点A 、B 、C 的距离分别为PA=4cm ，PB=5cm ，PC=2cm ，则点P 到直线l 的距离为不大于2cm ，故选：C ．【点睛】本题考查了点到直线的距离，点到直线的距离是点到直线的垂线段的长度，利用垂线段最短是解题关键． 6．用加减法解二元一次方程组233547x y x y -=⎧⎨+=⎩①②，下列步骤可以消去未知数x 的是( ) A ．43⨯+⨯①②B ．43⨯-⨯①②C ．52⨯+⨯①②D ．52⨯-⨯①② 【答案】D【解析】观察两方程中x 的系数，找出两系数的最小公倍数，即可做出判断．【详解】解：A 、可以消去yB 、不能消去x 或yC 、不能消去x 或yD 、可以消去x故选D ．【点睛】本题考查解二元一次方程组，利用消元的思想，消元的方法有：代入消元法与加减消元法．7． 的平方根是A ．B ．C ．D ．【答案】B【解析】根据平方根的定义求解. 【详解】∵, ∴的平方根是.故选：B.【点睛】考查了平方根的概念，解题关键是熟记平方根的定义.8．一艘轮船顺流航行，每小时行20km ；逆流航行，每小时行16m ，设轮船在静水中的速度为/xkm h ，水的流速为/ykm h ，根据题意，列方程组正确的是( )A ．2016x y x y +=⎧⎨-=⎩B ．2016y x y x +=⎧⎨-=⎩C ．1620x y x y +=⎧⎨-=⎩D ．1620y x y x +=⎧⎨-=⎩ 【答案】A【解析】根据题意，可以列出相应的方程组，本题得以解决．【详解】解：由题意可得，2016x y x y +=⎧⎨-=⎩， 故选：A ．【点睛】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组． 9．下列实数中，是无理数的为( )A．4B．38C．πD．1 3【答案】C【解析】分别根据无理数、有理数的定义即可判定选择项．【详解】解: 4=2,，38-=-2，0.33333……是有理数，π是无理数，故选：C.【点睛】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，2，0.8080080008…（每两个8之间依次多1个0）等形式．10．下列句子中，是命题的是( )A．画一个角等于已知角B．a、b两条直线平行吗C．直角三角形两锐角互余D．过一点画已知直线的垂线【答案】C【解析】分析是否是命题，需要分析是否是命题，需要分别分析各选项事是否是用语言、符号或式子表达的，可以判断真假的陈述句．别分析各选项事是否是用语言、符号或式子表达的，可以判断真假的陈述句．【详解】A、不符合命题的概念，故本选项错误；B、是问句，未做判断，故本选项错误；C、符合命题的概念，故本选项正确，D、因为不能判断其真假，故不构成命题，故此选项错误；；故选C．【点睛】本题考查了命题的定义：一般的，在数学中我们把用语言、符号或式子表达的，可以判断真假的陈述句叫做命题．二、填空题题11．如图，若在象棋盘上建立平面直角坐标系xOy，使“帥”的坐标为（﹣1，﹣2），“馬”的坐标为（2，﹣2），则“兵”的坐标为__．【答案】(-3,1)【解析】直接利用已知点坐标得出原点的位置进而得出答案．【详解】解：如图所示：“兵”的坐标为：（-3，1）．故答案为（-3，1）．【点睛】本题考查坐标确定位置，正确得出原点位置是解题关键．12．已知x ＝3是方程2x a -—2＝x —1的解，那么不等式(2—5a )x ＜13的解集是______． 【答案】x ＜19【解析】先根据x=3是方程2x a --2=x-1的解，代入可求出a=-5，再把a 的值代入所求不等式(2—5a )x ＜13，由不等式的基本性质求出x 的取值范围x ＜19． 故答案为：x ＜19. 13．已知点(2,27)A a a -+，B 点的坐标为(1,5)，直线//AB y 轴，则a 的值是__________．【答案】3【解析】根据AB ∥y 可知，A 点和B 点横坐标相等，然后把B 点横坐标代入A 点即可求出a 值.【详解】根据AB ∥y 可知，A 点和B 点横坐标相等，都为1，所以a-2=1，a=3【点睛】本题考查直线与坐标的位置关系，学生们掌握当与y 轴平行时，横坐标是相等的.14．如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段AB ,CD .则我们可以判定//AB CD 的依据是__________．【答案】内错角相等，两直线平行【解析】直接根据内错角相等，两直线平行即可解答.【详解】∵∠ADC=∠BAD=30°，∴AB//CD(内错角相等，两直线平行)，故答案为：内错角相等，两直线平行.【点睛】本题考查了平行线的判定，熟练掌握内错角相等，两直线平行是解本题的关键.15．十二边形的内角和度数为_________.【答案】1800°【解析】根据n边形的内角和是（n﹣2）•180°，把多边形的边数代入公式，就得到多边形的内角和．【详解】解：十二边形的内角和为：（n﹣2）•180°=（12﹣2）×180°=1800°．故答案为1800°．【点睛】本题考查了多边形的内角和的知识，解决本题的关键是正确运用多边形的内角和公式，要求同学们熟练掌握．16．山上的一段观光索道如图所示，索道支撑架均为相平行（AM∥CN），且每两个支撑架之间的索道均是直的，若∠MAB＝60°，∠NCB＝40°，则∠ABC＝_____°．【答案】1°【解析】利用平行线的性质得到∠ABE＝∠MAB＝60°，∠CBE＝∠NCB＝40°，然后计算∠ABE+∠CBE即可．【详解】解：如图，延长DB 至点E，∵AM∥BD，∴∠ABE＝∠MAB＝60°，∵CN∥BD，∴∠CBE＝∠NCB＝40°，∴∠ABC＝∠ABE+∠CBE＝60°+40°＝1°．故答案为1．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．17．如图，在ABC ∆中，DE 是BC 的垂直平分线，若8AC cm =，ABE ∆的周长为13cm ，则AB 的长为__________．【答案】5cm【解析】根据垂直平分线的性质可知BE=CE ，所以ABE ∆的周长=+AB AC ，由此可得AB 的长. 【详解】解：DE 是BC 的垂直平分线BE CE ∴=13ABE C AB BE AE AB CE AE AB AC ∆∴=++=++=+=又8AC =135AB AC ∴=-=故答案为：5cm【点睛】本题考查了线段垂直平分线的性质，灵活应用此性质进行线段的转化是解题的关键.三、解答题18．解不等式或不等式组，并把它的解集表示在数轴上: (1) 41(2)(2)3x x -->-; (2) 24543x x x -<⎧⎨+⎩①② 【答案】（1）5x <，把它的解集表示在数轴上见解析；（2）23x -<，把它的解集表示在数轴上见解析.【解析】（1）按照移项、合并同类项、去分母、化系数为1的步骤解方程即可；（2）首先分解解出两个不等式，再根据大大小小找不到确定不等式组的解集．【详解】(1)移项，得1(2)13x -<去分母，得23x -<,移项，得5x <..不等式组的解集为5x <.(2)24543x x x -<⎧⎨+⎩①② 解不等式①，得2x ->. .解不等式②,得3x .原不等式组的解集为23x -<【点睛】此题考查解一元一次不等式组，解一元一次不等式，在数轴上表示不等式的解集，解题关键在于掌握运算法则.19．周六的早上,小颖去郑州图书大厦买书.她先走到早餐店吃早餐,然后又去图书大厦买书,最后又回到家.如图是小颖所用的时间 x(分)和离家的距离 y(千米)之间的示意图,请根据图像解答下列问题(1)在上述变化过程中,自变量是 ，因变量是 ；(2)早餐店到小颖家的距离是 千米,她早餐花了 分钟(3)出发后37分到55分之间小颖在干什么?(4)小颖从图书大厦回家的过程中,她的平均速度是多少?【答案】（1）时间x ，离家的距离y ；（2）1.1，10；（3）小颖在图书大厦买书；（4）80米/分.【解析】理解题意，根据题意对照图象进行分析即可.注意理解函数图象的意义.【详解】解：（1）时间x ，离家的距离y ；（2）观察坐标轴可得：1.1，10；（3）根据题意描述可知：小颖在图书大厦买书；（4）2000(8055)80÷-=（米/分）.答：小颖从图书大厦回家的过程中，她的平均速度是80米/分.【点睛】考核知识点：实际问题与函数图象.理解题意是关键.20．如图，已知AB∥CD不添加任何字母和数字，请你再添加一个条件∠1=∠2成立(要求给出三个答案)，并选择其中一种情况加以证明.条件1：________________________________；条件2：________________________________；条件3：________________________________.【答案】(1)∠EBC=∠FCB，CF∥BE，∠E=∠F ；(1)证明见解析【解析】根据题意可添加条件：①CF∥BE；②∠FCB=∠EBC；③∠E=∠F；选择①进行证明：根据平行线的性质可得∠ABC=∠DCB，∠FCB=∠EBC，由∠ABC-∠EBC =∠DCB-∠FCB即可证得结论.【详解】条件1：CF∥BE；条件1：∠FCB=∠EBC；条件3：∠E=∠F；选择：CF∥BE．证明：∵AB∥CD，∴∠ABC=∠DCB，又∵CF∥BE，∴∠FCB=∠EBC，∴∠ABC-∠EBC =∠DCB-∠FCB，即∠1=∠1．【点睛】本题考查了平行线的性质，熟练运用平行线的性质是解决问题的关键.21．解不等式组3(2)41213x xxx--≥-⎧⎪+⎨>-⎪⎩，并把它们的解集在数轴上表示出来.【答案】x≤1.【解析】分析：先分别解两个不等式得到x≥1和x＜4，再根据大于小的小于大的取中间确定不等式组的解集，然后用数轴表示解集．详解：()3241213x xxx⎧--≥-⎪⎨+>-⎪⎩①②解不等式①，得1x≤解不等式②，得x<4x ，所以原不等式组的解集是1将其解集表示在数轴上如下：点睛：本题考查了解一元一次不等式组：分别求出不等式组各不等式的解集，然后根据“同大取大，同小取小，大于小的小于大的取中间，大于大的小于小的无解”确定不等式组的解集．也考查了在数轴上表示不等式的解集．22．如图，△ABC中，∠C=45°，∠A=55°，BE是△ABC角平分线，点D在AB上，且DE∥BC，求∠DEB的度数．【答案】∠DEB=40°．【解析】依据三角形内角和定理即可得到∠ABC=80°，再根据角平分线的定义以及平行线的性质，即可得出∠DEB的度数．【详解】解：∵∠C=45°，∠A=55°，∴∠ABC=80°，又∵BE平分∠ABC，∴∠CBE=40°，∵DE∥BC，∴∠DEB=∠CBE=40°．【点睛】本题考查的是三角形内角和定理以及平行线的性质的运用，熟知三角形内角和是180°是解答此题的关键．23．在直角三角形中，两条直角边的长度分别为a和b，斜边长度为c，则a2＋b2＝c2，即两条直角边的平方和等于斜边的平方，此结论称为勾股定理．在一张纸上画两个同样大小的直角三角形ABC和A′B′C′，并把它们拼成如图所示的形状 (点C和A′重合，且两直角三角形的斜边互相垂直)．请利用拼得的图形证明勾股定理．【答案】见解析【解析】连接,梯形的面积等于上底加下底的和乘以高除以2，,用字母表示出来,化简后,即可得证.【详解】如图所示，在Rt △ABC 中，∵∠1＋∠2＝90°，∠1＝∠3，∴∠2＋∠3＝90°.又∵∠ACC′＝90°，∴∠2＋∠3＋∠ACC′＝180°，∴B ，C(A′)，B′在同一条直线上．又∵∠B ＝90°，∠B′＝90°，∴∠B ＋∠B′＝180°，∴AB ∥C′B′. 由面积相等得(a ＋b)(a ＋b)＝ab ＋ab ＋c 2，即a 2＋b 2＝c 2.【点睛】本题考查了勾股定理的证明，掌握梯形的面积公式并能正确作出辅助线是解题的关键.24．如图，在'''ABC A B C ∆∆和中，已知'A A ∠=∠，'B B ∠=∠，''AB A B =，试把下面运用“叠合法”说明ABC ∆和'''A B C ∆全等的过程补充完整：说理过程：把ABC ∆放到'''A B C ∆上，使点A 与点'A 重合，因为 ，所以可以使 ，并使点C 和'C 在AB （''A B ）同一侧，这时点A 与'A 重合，点B 与'B 重合，由于 ，因此， ；由于 ，因此， ；于是点C （射线AC 与BC 的交点）与点'C （射线''A C 与''BC 的交点）重合，这样 ．【答案】见解析．【解析】根据“叠合法”说明两三角形全等即可．【详解】说理过程：把ABC ∆放到'''A B C ∆上，使点A 与点'A 重合，因为''AB A B =，所以可以使AB 与''A B 重合，并使点C 和'C 在AB （''A B ）同一侧，这时点A 与'A 重合，点B 与'B 重合，由于'A A ∠=∠，因此， 射线AC 与射线''A C 叠合 ；由于 B B'∠=∠，因此，射线BC 与射线''B C 叠合；于是点C （射线AC 与BC 的交点）与点'C （射线''A C与''B C 的交点）重合，这样'''ABC A B C ∆∆与重合，即'''ABC A B C ∆∆与全等．【点睛】本题主要考查三角形全等的定义，掌握“叠合法”说明三角形全等，是解题的关键．25．（1）化简：a b b a ab a b +⎛⎫÷- ⎪⎝⎭，当a 为4的算术平方根，3b =时，求这个代数式的值； （2）计算：()3216812(4)(23)(32)x x x x x x -+÷----．【答案】（1）1b a-，1；（2）212x -+ 【解析】（1）根据算术平方根的概念求出a 的值，化简分式，然后把将a 、b 的值代入计算； （2）先计算括号里的，然后算乘除法．【详解】解：（1）a 为4的算术平方根，2a ∴=． 原式221()()a b b a a b ab ab ab ab a b b a b a⎛⎫+-+=÷=⋅= ⎪+--⎝⎭， 将2a =，3b =代入得，原式1132==-． （2）原式()22224234942349212x x x x x x x =-+--=-+-+=-+．【点睛】本题考查了分式的化简求值以及整式的混合运算，熟练运用分式的混合运算法则以及整式的运算发则是解题的关键．七年级下学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，点C 在射线BE 上，不能判定//AB CD 的是（ ）A ．B DCE ∠=∠B ．A ACD ∠=∠C ．A DCE ∠=∠D ．180B BCD ∠+∠=︒【答案】C 【解析】利用平行线的判定方法一一判断即可．【详解】由∠B=∠DCE,根据同位角相等两直线平行,即可判断AB ∥CD.由∠A=∠ACD,根据内错角相等两直线平行,即可判断AB ∥CD.由∠B+∠BCD=180∘,根据同旁内角互补两直线平行,即可判断AB ∥CD.故A ，B ，D 不符合题意，由A DCE ∠=∠不能判定AB ∥CD ，故选C.【点睛】此题主要考查平行线的判定，解题的关键是熟知平行线的判定定理.2．如图，把长方形ABCD 沿EF 按图那样折叠后，A 、B 分别落在点G 、H 处，若∠1=50°，则∠AEF=（ ）A ．110°B ．115°C ．120°D ．125°【答案】B 【解析】解：∵四边形ABCD 为长方形，∴AE ∥BF ，∠AEF+∠BFE=180°；由折叠变换的性质得：∠BFE=∠HFE ，而∠1=50°，∴∠BFE=（180°﹣50°）÷2=65°，∴∠AEF=180°﹣65°=115°．故选B ．点睛：该题主要考查了翻折变换的性质、矩形的性质、平行线的性质及其应用问题；应牢固掌握矩形的性质、平行线的性质等几何知识点．3．已知方程组2225325x y m x y m -=⎧⎨+=+⎩的解x 、y 互为相反数，则m 的值为（ ）. A ．-1B ．0C ．5D ．-5【答案】D【解析】分析：由已知得x+y=0，方程组中两方程和等于x+y=5m+25,从而求出m 的值．详解：22 25325x y mx y m①②-=⎧⎨+=+⎩①+②，得：x+y=5m+25,又x+y=0，∴5m+25=0∴m=-5故选D.点睛：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．4．下列数据中，无理数是()A．2-B．0 C．227D．π【答案】D【解析】根据无理数的定义即可求出答案．【详解】解：无限不循环的小数为无理数，故选：D．【点睛】本题考查无理数，解题的关键是正确理解无理数的定义，本题属于基础题型．5．不考虑优惠，买1本笔记本和3支水笔共需14元，买3本笔记本和5支水笔共需30元，则购买1本笔记本和1支水笔共需（）A．3元B．5元C．8元D．13元【答案】C【解析】设每个笔记本x元，每支钢笔y元，根据题意列出方程组求解即可【详解】设购买1本笔记本需要x元，购买1支水笔需要y元，根据题意，得+314 3530x yx y=⎧⎨+=⎩．解得53xy=⎧⎨=⎩．所以x+y＝5+3＝8（元）故选C．【点睛】此题主要考查二元一次方程组的应用，难度不大，关键在于列出方程组6．2-的相反数是（）A．2-B．2 C．12D．12-【答案】B。

○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前沪教版2018--2019学年度第二学期七年级期末考试数学试卷题号 一 二 三 总分 得分注意事项：1．做卷时间100分钟，满分120分 2．做题要仔细，不要漏做 评卷人 得分一、单选题(计30分）1．（本题3分）计算9的结果是( ) A ．3 B ．3± C ．3- D ．92．（本题3分）在实数－3、0，π、3中，最大的实数是（ ） A ．－3 B ．0 C ．π D ．33．（本题3分）工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB 是一个任意角，在边 OA 、 OB 上分别取OM=ON ，移动角尺，使角尺两边相同的刻度分别与点 M 、N 重合，过角尺顶点 C 作射线 OC ．由此．．作法便可得△MOC ≌△NOC ，其依据是（ ）A ．SSSB ．SASC ．ASAD ．AAS 4．（本题3分）若实数x 、y 满足+(y-8)2=0，则以x 、y 的值为两边长的等腰三角形的周长是( )A ．18B ．21C ．18或24D ．18或215．（本题3分）∠AOB 的平分线上一点P 到OA 的距离为6，Q 是OB 上任一点，则 ( )○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※○…………内…………○…………装…………○…………订…………○…………线…………○…………A ．PQ>6B ．PQ≥6C ．PQ<6D ．PQ≤66．（本题3分）已知a ∥b ，某学生将一直角三角板放置如图所示，如果∠1=35°，那么∠2的度数为（ ）A ．35°B ．55°C ．56°D ．65°7．（本题3分）若等腰三角形的周长为16cm ，其中一边长为4cm ，则该等腰三角形的底边为（ ）A ．4cmB ．6cmC ．4cm 或8cmD ．8cm8．（本题3分）如果P （a-1，a+2）在x 轴上，那么点P 的坐标是（ ） A ．（-3，0） B ．（0，3） C ．（0，-3） D ．（3，0） 9．（本题3分）如图,直线a 、b 相交,∠1=130°,则∠2+∠3=( )A ．50°B ．100°C ．130° C.180°10．（本题3分）用直尺和圆规作一个角的平分线如示意图所示,能说明∠AOC=∠BOC 的依据是（ ）A ．角平分线上的点到角两边距离相等B ．ASAC ．SSSD ．AAS○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○…………11．（本题4分）的平方根是_____；的绝对值是_____．12．（本题4分）等腰三角形的一边长为7cm ，另一边长为3cm,那么这个等腰三角形的周长为________cm.13．（本题4分）计算：|﹣7|++= ．14．（本题4分）如图，直线，直线EF 与AB 、CD 相交于点E 、F ，的平分线EN 与CD 相交于点若，则_____．15．（本题4分）如图，∠ABC =∠DAB ，若以“SAS ”为依据，使△ABC ≌△BAD ，还要添加的条件是____________；（用图中字母表示）16．（本题4分）如图，若AB ∥CD ，∠1＝65°，则∠2的度数为____°．17．（本题4分）一个正三角形和一副三角板（分别含30°和45°）摆放成如图所示的位置，且AB ∥CD ．则∠1＋∠2＝__________．18．（本题4分）如图，在中，AD 是高，AE 是角平分线，若，，○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※○…………内…………○…………装…………○…………订…………○…………线…………○…………评卷人 得分三、解答题（计58分）19．（本题7分）计算|﹣5|+327﹣（13）﹣1．20．（本题7分）计算：．21．（本题7分）尺规作图：已知∠α，线段a, b（1）求作：△ABC，使∠A=∠α, AB=a,AC=b。

绝密★启用前 沪教版2018--2019学年度第二学期七年级期末复习 数学试卷 注意事项： 1．做卷时间100分钟，满分120分 2．做题要仔细，不要漏做一、单选题(计30分） 1．（本题3分）在下列四个图案中，能用平移变换来分析其形成过程的图案是 ( ) A ． B ． C ． D ． 2．（本题3分）下列说法正确的有( ) ①0的算术平方根是0； ②8的算术平方根是4； ③±是11的平方根； ④-5是25的一个平方根； ⑤±2是8的立方根； ⑥81的平方根是9. A ．1个 B ．2个 C ．3个 D ．4个 3．（本题3分）若关于x 的不等式（a ﹣1）x ＜3（a ﹣1）的解都能使不等式x ＜5﹣a 成立，则a 的取值范围是（ ） A ．a ＜1或a ≥2 B ．a ≤2 C ．1＜a ≤2 D ．a ＝2 4．（本题3分）不等式组的解集在数轴上表示为( ) A ． B ． C ． D ． 5．（本题3分）下列各式可以用平方差公式分解因式的是（ ） A ．-m 2n 2+1； B ．-m 2n 2-1； C ．m 2n 2+1； D ．(mn +1) 2； 6．（本题3分）已知16x 2+4mx +9是完全平方式，则m 的值为（ ） A ．12 B ．±12 C ．-6 D ．±6A ．B ．C ．D ． 8．（本题3分）如图，直线l 1∥l 2，将一直角三角尺按如图所示放置，使得直角顶点在直线l 1上，两直角边分别与直线l 1、l 2相交形成锐角∠1、∠2且∠1＝25°，则∠2的度数为（ ） A ．25° B ．75° C ．65° D ．55°9．（本题3分）已知a ＝（-3)21 ，b ＝(－2)2，c ＝(π－2018)0，则a ，b ，c 的大小关系是( )A ．b <a <cB ．b <c <aC ．c <b <aD ．a <c <b10．（本题3分）甲、乙两人分别从距目的地6千米和10千米的两地同时出发，甲、乙的速度比是，结果甲比乙提前20分钟到达目的地，求甲、乙的速度．若设甲的速度为千米/时，乙的速度为千米/时．则所列方程是（ ）A ．B ．C ．D ．二、填空题（计32分）11．（本题4分）请你写出一个大于2小于3的无理数是______．12．（本题4分）若3m-12与12-3m 都有平方根，则m 的平方根为_________13．（本题4分）不等式组 的正整数的解的和是________________． 14．（本题4分）因式分解：27a 3﹣3a ＝_____．15．（本题4分）计算__________.16．（本题4分）若关于x 的方程=﹣1无解，则m 的值是____．17．（本题4分）将含有30°角的三角板的直角顶点放置于互相平行的两条直线中的一条上(如图)，如果∠1=40°，那么∠2=_________18．（本题4分）已知：如图，AB ∥CD ，EF ∥CD ,且∠ABC =20°，∠CFE =30°,则∠BCF 的度数是___________．三、解答题（计58分） 19．（本题7分）计算： 20．（本题7分）解不等式组 ． 21．（本题7分）因式分解 （1） （2）22．（本题7分）先化简，再求值，（3x+1）（3x ﹣1）﹣4（x ﹣2）﹣（3x ﹣1）2，其中x=﹣31． 23．（本题7分）先化简，再求值：，其中﹣1＜x ＜3，选择一个你喜欢的整数x 代入求值．24．（本题7分）如图,AB ∥CD,点P 在AB,CD 内部,则∠B,∠D,∠BPD 之间有何数量关系?证明你的结论25．（本题8分）如图，直线AB ，CD ，EF 相交于点O.(1)分别写出∠COE 的邻补角和∠BOE 的对顶角；(2)如果∠BOD ＝60°，∠BOF ＝90°，求∠FOC 的度数．26．（本题8分）如图，点D 、F 在线段AB 上，点E 、G 分别在线段BC 和AC 上，CD ∥EF ，∠1=∠2. (1)判断DG 与BC 的位置关系，并说明理由； (2)若DG 是∠ADC 的平分线，∠3=85°，且∠DCE :∠DCG =9:10，AB 与CD 有怎样的位置关系?并说明理由.参考答案1．B【解析】【分析】根据平移不改变图形的形状和大小，将题中所示的图案通过平移后可以得到的图案是B．【详解】解：观察图形可知图案B通过平移后可以得到．故选：B．【点睛】本题考查图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．2．C【解析】【分析】利用立方根、平方根和算术平方根的定义进行判断即可得到正确的答案．【详解】解：①0的算术平方根是0，故正确；②8的算术平方根是2，故错误；③±是11的平方根，故正确；④-5是25的平方根，正确；⑤8的立方根只有2，故错误；⑥∵(±9)²=81，∴81的平方根是±9，故错误．正确的有三个，故选：C．【点睛】本题考查了立方根、平方根及算术平方根的知识，属于基础题，比较简单．3．C【解析】【分析】根据关于x的不等式（a﹣1）x＜3（a﹣1）的解都能使不等式x＜5﹣a成立，列出关于a的不等式，即可解答．【详解】解：∵关于x的不等式（a﹣1）x＜3（a﹣1）的解都能使不等式x＜5﹣a成立，∴a﹣1＞0，即a＞1，解不等式（a﹣1）x＜3（a﹣1），得：x＜3，则有：5﹣a≥3，解得：a≤2，则a的取值范围是1＜a≤2．故选：C．【点睛】本题考查了解一元一次不等式以及解一元一次不等式组，解不等式要依据不等式的基本性质：（1）不等式的两边同时加上或减去同一个数或整式，不等号的方向不变；（2）不等式的两边同时乘以或除以同一个正数，不等号的方向不变；（3）不等式的两边同时乘以或除以同一个负数，不等号的方向改变．4．A【解析】【分析】先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．【详解】由3x-2＞1，解得x＞1，3-2x≥-1，解得xx≤2，不等式组的解集为1＜x≤2，在数轴上表示为：故选A．【点睛】本题考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．5．A【解析】【分析】根据平方差公式的性质特点即可判断.【详解】A. -m2n2+1，有两项平方项，符号相反，故可用平方差公式进行因式分解；B. -m2n2-1，有两项平方项，符号相同，故不可用平方差公式进行因式分解；C. m2n2+1，有两项平方项，符号相同，故不可用平方差公式进行因式分解；D. (mn+1) 2，为完全平方式，故错误故选A.【点睛】此题主要考查因式分解的方法，解题的关键是熟知平方差公式的特点. 6．D【解析】【分析】根据完全平方公式的特点即可进行求解.【详解】∵16x2+4mx+9=(4x)2+4mx+32∴4m=±24,∴m=±6故选D【点睛】此题主要考查完全平方公式，解题的关键是熟知完全平方公式的特点.7．B【解析】【分析】先根据乘方运算法则、负整数指数幂及零指数幂分别计算，再判断大小即可得．【详解】解：a=0.32=0.09，b= -3-2=，c=（-3）0=1，∴c＞a＞b，故选：B．【点睛】本题考查有理数的大小比较，解题的关键是熟练掌握乘方运算法则、负整数指数幂及零指数幂．8．C【解析】【分析】依据∠1＝25°，∠BAC＝90°，即可得到∠3＝65°，再根据平行线的性质，即可得到∠2＝∠3＝65°．【详解】如图，∵∠1＝25°，∠BAC＝90°，∴∠3＝180°-90°-25°=65°，∵l1∥l2，∴∠2＝∠3＝65°，故选C．【点睛】本题考查的是平行线的性质，运用两直线平行，同位角相等是解答此题的关键．9．C【解析】【分析】直接利用负指数幂的性质以及零指数幂的性质分别化简得出答案．【详解】a=（）-3=8，b=（-2）2=4，c=（π-2018）0=1，则c＜b＜a．故选：C．【点睛】此题主要考查了负指数幂的性质以及零指数幂的性质，正确化简各数是解题关键．10．C【解析】【分析】甲的速度为千米/时，乙的速度为千米/时，则可求出甲所用时间为，甲所用时间为，再利用甲比乙提前20分钟到达即可列出方程.【详解】甲的速度为千米/时，乙的速度为千米/时，依题意可得.故选C.【点睛】此题主要考查分式方程的应用，解题的关键是找到等量关系，并进行统一单位.11．【解析】【分析】根据算术平方根的性质可以把2和3写成带根号的形式，再进一步写出一个被开方数介于两者之间的数即可．【详解】∵2=，3=，∴写出一个大于2小于3的无理数是等．故答案为等．本题答案不唯一．【点睛】此题考查了无理数大小的估算，熟悉算术平方根的性质是关键．12．±2.【解析】【分析】根据非负数有平方根，求出m的值，再求m的平方根即可.【详解】由题意得，3m−12≥0，则m≥412−3m≥0，则m≤4，∴m=4m的平方根为±2.故答案为：±2.【点睛】考查平方根的定义，求出m的值是解题的关键.13．6【解析】【分析】根据题意将不等式组解出来得到0≤x≤3，故正整数解有1,2,3,三个数，加起来得到和为6. 【详解】解：解得故不等式组的正整数解有1，2，31+2+3=6，故答案为6.【点睛】本题考查不等式组的解法，解本题的关键是看清楚题，题目要求求正整数的解的和. 14．3a(3a+1)(3a﹣1【解析】【分析】原式提取公因式，再利用平方差公式分解即可．【详解】原式＝3a(9a2﹣1)＝3a(3a+1)(3a﹣1)，故答案为：3a(3a+1)(3a﹣1)【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．15．1【解析】【分析】根据负整数指数幂，零指数幂和绝对值的意义，按照有理数混合运算的顺序，先乘方后乘除最后算加减即可求出结果.【详解】解：=161-15=1.【点睛】此题考查负整数指数幂，零指数幂和绝对值，有理数的混合运算，熟练掌握运算法则和性质是关键．16．1或.【解析】【分析】分式方程去分母转化为整式方程，由分式方程无解确定出x的值，代入整式方程计算即可求出m的值．【详解】解：去分母得：3-2x+mx-2=-x+3，整理得：（m-1）x=2，当m-1=0，即m=1时，方程无解；当m-1≠0时，x-3=0，即x=3时，方程无解，此时，即，故答案为：1或.【点睛】此题考查了分式方程的解，分式方程无解分为最简公分母为0的情况与分式方程转化为的整式方程无解的情况．17．20°【解析】【分析】如图所示，过E点作EF∥AB，利用平行线的性质解答即可．【详解】解：过E点作EF∥AB，如图，∵EF∥AB，AB∥CD，∴EF∥AB∥CD，∴∠1=∠GEF=40°，∠2=∠HEF，∵∠GEF+∠HEF=60°，∴∠2=60°- 40°=20°，故答案为：20°．【点睛】此题主要考查了平行线的性质，熟练掌握平行线的性质是解题关键．18．【解析】【分析】根据平行线的性质，由AB∥CD得∠BCD=∠ABC=20°，由EF∥CD得∠DCF=∠CFE=30°，然后利用∠BCF=∠BCD+∠DCF进行计算即可．【详解】∵AB∥CD，∴∠BCD=∠ABC=20°，∵EF∥CD，∴∠DCF=∠CFE=30°，∴∠BCF=∠BCD+∠DCF=50°．故答案是：50°．【点睛】考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．19．【解析】【分析】先计算立方根和算数平方根，然后再计算减法即可.【详解】解：=5－－=5－－2=.【点睛】本题主要考查了求一个数的立方根和平方根，以及根式的减法运算，正确求出立方根和平方根是解题的关键.20．﹣2＜x≤1【解析】【分析】先求出两个不等式的解集，再求其公共解．【详解】解：，由①得，x＞﹣2，由②得，x≤1，所以不等式组的解集为﹣2＜x≤1．【点睛】本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．21．（1）4（x＋2）（x－2）；（2）－b（2a－b）2；【解析】【分析】(1)先提取公因式4，再对余下的多项式利用平方差公式继续分解；(2) 应先提取公因式-b，再利用完全平方公式继续进行因式分解.【详解】（1）原式=4（x2－4）=4（x＋2）（x－2）；（2）原式=－b（4a2－4ab＋b2）=－b（2a－b）2；【点睛】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．22．【解析】【分析】根据平方差公式与完全平方公式即可进行化简，再进行合并即可求解.【详解】原式=9x2-1-4x+8-(9x2-6x+1)=9x2-4x+7-9x2+6x-1=2x+6当x=时，原式=2×（）+6=【点睛】此题主要考查整式的化简求值，解题的关键是熟知公式的运用.23．，2.【解析】【分析】根据分式的混合运算顺序和运算法则化简原式，再选取使分式有意义的x的值代入计算可得．【详解】原式＝[]•＝•＝，当x＝2时，原式＝2．【点睛】本题考查了分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则．24．∠B+∠D=∠BPD【解析】【分析】作PE∥AB，则PE∥AB∥CD，根据平行线的性质即可求解.【详解】∠B+∠D=∠BPD，证明如下：作PE∥AB，则PE∥AB∥CD，∴∠B=∠BPE，∠D=∠DPE，∵∠BPD=∠BPE+∠DPE∴∠B+∠D=∠BPD【点睛】此题主要考查平行线的性质，解题的关键是根据题意作出辅助线.25．（1）∠COE的邻补角为∠COF和∠DOE，∠BOE的对顶角为∠AOF.（2）150°.【解析】【分析】（1）根据邻补角与对顶角的定义即可写出；（2）根据角的和差与邻补角的性质即可求解.【详解】（1）∠COE的邻补角为∠COF和∠DOE，∠BOE的对顶角为∠AOF.（2）∵∠BOD＝60°，∠BOF＝90°，∴∠DOF=90°-∠BOD=30°，∴∠FOC=180°-∠DOF=150°.【点睛】此题主要考查角的计算，解题的关键是邻补角与对顶角的性质.26．(1)DG∥BC．理由见解析. (2)CD⊥AB．理由见解析.【解析】【分析】（1）先根据CD∥EF得出∠2=∠BCD，再由∠1=∠2得出∠1=∠BCD，进而可得出结论；（2）根据DG∥BC，∠3=85°得出∠BCG的度数，再由∠DCE：∠DCG=9：10得出∠DCE 的度数，根据DG∥BC可得∠1=∠DCE，求出∠1的度数.由DG是∠ADC的平分线可得出∠ADC的度数，由此得出结论．【详解】（1）DG∥BC．理由：∵CD∥EF，∴∠2=∠BCD．∵∠1=∠2，∴∠1=∠BCD，∴DG∥BC；（2）CD⊥AB．理由：∵由（1）知DG∥BC，∠3=85°，∴∠BCG=180°-85°=95°．∵∠DCE：∠DCG=9：10，∴∠DCE=95°×=45°∴∠1=∠DCE=45°∵DG是∠ADC的平分线，∴∠ADC=2∠1=90°，∴CD⊥AB．【点睛】本题考查的是平行线的判定与性质，熟知平行线的性质与判定定理及角平分线的定义是解答本题的关键.。

七年级下学期期末数学试卷一、选择题（每题只有一个答案正确）1．下列二次根式中，最简二次根式的是（）A．15B．0.5C．5D．50【答案】C【解析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【详解】A、15=5，被开方数含分母，不是最简二次根式；故A选项错误；B、0.5=22，被开方数为小数，不是最简二次根式；故B选项错误；C、5，是最简二次根式；故C选项正确；D．50=52，被开方数，含能开得尽方的因数或因式，故D选项错误；故选C．考点：最简二次根式．2．甲乙两家公司在去年1-8月份期间的赢利情况，统计图如图所示，下列结论不正确的是（）A．甲公司的赢利正在下跌B．乙公司的赢利在1-4月间上升C．在8月，两家公司获得相同的赢利D．乙公司在9月份的赢利定比甲的多【答案】D【解析】根据折线统计图中所反映的数据增减变化情况，这个做出判断即可，【详解】解：由折线统计图可以看出：甲1-8分的盈利的曲线呈下降趋势，因此盈利在逐月下跌，A的判定是正确的，乙公司1-4月份盈利曲线是上升的，因此B的判定是正确的8月时，甲、乙公司的盈利是一样的，因此C的判定是正确的，9月的盈利很难取得谁的多、谁的少，不确定因此D的判定是错误的，故选D ．【点睛】考查从折线统计图中获取数据做出分析的能力，正确识图数据做出判断的前提和关键．3．如果点在轴上，则点所在的象限是（ ） A ．第四象限B ．第三象限C ．第二象限D ．第一象限【答案】A 【解析】根据轴上的点横坐标为0,列方程求出m ，然后可得Q 点坐标，再判断即可.【详解】解：由题意得：m ＋1＝0，解得：m ＝−1，m 2019＝（−1）2019＝−1∴Q （2，−1），∴Q 在第四象限．故选：D ．【点睛】本题考查了平面直角坐标系，正确理解横坐标与纵坐标的意义是解题的关键．4．计算2a 3b·(-3b 2c)÷(4ab 3)，所得的结果是（ ）A ．a 2bcB ．a 2cC ．acD ．a 2c 【答案】D【解析】根据整式的乘法和除法的运算法则按顺序计算即可.【详解】2a 3b·(-3b 2c)÷(4ab 3) =-6a 3b 3c÷(4ab 3) =a 2c故选D.【点睛】本题考查整式的乘法和除法，熟练掌握运算法则是解题关键.5．问题“鸡兔同笼，共有30个头，88只脚．问笼中鸡兔各有多少只？”若设鸡有x 只，则下列方程正确的是（ ）A ．42(30)88x x +-=B ．24(30)88x x +-=C ．42(88)30x x +-=D ．24(88)30x x +-=【答案】B【解析】设鸡有x 只，根据题意即可列出一元一次方程．【详解】设鸡有x 只，根据题意可得方程：24(30)88x x +-=,故选B ．【点睛】此题主要考查一元一次方程的应用，解题的关键是根据题意列出方程．6．用计算器求53的值时，需相继按“3”“x y ”“5”“=”键，若小颖相继按x y ”“3”“=”键，则输出结果是（ ）A ．6B ．8C ．16D ．48 【答案】B【解析】根据题目可将计算器按键转为算式3求解．【详解】解：将计算器按键转为算式为：3328==，故选：B ．【点睛】本题考查的知识点是数的开方，将题目中的计算器按键转为算式3是解题的关键． 7．某种服装的进价为 240 元，出售时标价为 330 元，由于换季，商店准备打折销售，但要保持利润不低于 10%，那么至多打（ ）A ．6 折B ．7 折C ．8 折D ．9 折【答案】C【解析】设打了x 折，用售价×折扣-进价得出利润，根据利润率不低于10%，列不等式求解．【详解】解：设打了x 折，由题意得330×0.1x-240≥240×10%，解得：x≥1．答：至多打1折．故选：C ．【点睛】本题考查一元一次不等式的应用，解答本题的关键是读懂题意，求出打折之后的利润，根据利润率不低于10%，列不等式求解．8．下列运算正确的是（ ）A ．（﹣2a ）3=﹣6a 3B ．﹣3a 2•4a 3=﹣12a 5C ．﹣3a （2﹣a ）=6a ﹣3a 2D ．2a 3﹣a 2=2a 【答案】B【解析】先根据同底数幂的乘法法则进行运算即可。

2018-2019学年七年级（下）期末数学试卷一、选择题1）A．±9 B．9 C．3 D．±32．下列实数3.1415，﹣23）A．1个 B．2个 C．3个 D．4个3．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是（）A B C D4．若m＞n＞0，则下列不等式一定成立的是（）A 1 B．m﹣n＜0 C．﹣m＜﹣n D．m+n＜05．（2x+1）=2x2+mx+n，则m，n的值分别是（）A．5，﹣3 B．﹣5，3 C．﹣5，﹣3 D．5，36．如图，已知AC∥BD，∠CAE=30°，∠DBE=45°，则∠AEB等于（）A．30°B．45°C．60°D．75°7．如图，以下条件能判定GE∥CH的是（）A．∠FEB=∠ECD B．∠AEG=∠DCH C．∠GEC=∠HCF D．∠HCE=∠AEG8的解为（）A．x=4 B．x=3 C．x=0 D．无解9．将分式方程1）A．8x+1=0 B．8x﹣3=0 C．x2﹣7x+2=0 D．x2﹣7x﹣2=010．为改善生态环境，某村拟在荒土上种植960棵树，由于青年团的支持，每日比原计划多种20棵，结果提前4天完场任务，原计划每天种植多少棵？设原计划每天种植x棵，下面方程正确的是（）A BC D二、填空题11．一个正方形的面积是20，通过估算，它的边长在整数与之间．12．不等式2﹣x＜2x+5的解集是．13．分解因式：9x2﹣4y2=．14．当x时，分式15．观察下列各式：13=1213+23=3213+23+33=6213+23+33+43=102…猜想13+23+33+…+103=．三、解答题16．计算（1）|﹣1|（π﹣3）0+2﹣2（2）（a+2b）（a﹣2b）（a2+4b2）17．解方程（1）3（2x﹣1）2﹣27=0（21819x+3）x=3．20．如图，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD．21．李明到离家2.1千米的学校参加初三联欢会，到学校时发现演出道具还放在家中，此时距聚会还有42分钟，于是分立即步行（匀速）回家，在家拿道具用了1分钟，然后骑自行车（匀速）返回学校，已知李明骑自行车的速度是步行速度的3倍，李明骑自行车到学校比他从学校步行到家少用了20分钟．（1）李明步行的速度是多少米/分？（2）李明能否在联欢会开始前赶到学校？22．观察下列各式：，…（1=；（2）猜想出能表示上述特点的一般规律，用含字母n的等式表示出来（n是正整数）；（3）请用（2…果．2018-2019学年七年级（下）期末数学试卷参考答案与试题解析一、选择题1）A．±9 B．9 C．3 D．±3【考点】算术平方根；平方根．，求出9的平方根即可．=9，3，故选D．【点评】本题考查了对平方根和算术平方根的应用，主要考查学生理解能力和计算能力．2．下列实数3.1415，﹣23）A．1个 B．2个 C．3个 D．4个【考点】无理数．【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．故选：B．【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．3．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是（）A B C D【考点】生活中的平移现象．【分析】根据平移的性质，结合图形对选项进行一一分析，选出正确答案．【解答】解：A、图形的形状和大小没有变化，符合平移的性质，属于平移得到；B、图形的大小发生变化，不符合平移的性质，不属于平移得到；C、图形的方向发生变化，不符合平移的性质，不属于平移得到；D、图形由轴对称得到，不属于平移得到．故选A．【点评】本题考查平移的基本性质，平移不改变图形的形状、大小和方向．注意结合图形解题的思想．4．若m＞n＞0，则下列不等式一定成立的是（）A 1 B．m﹣n＜0 C．﹣m＜﹣n D．m+n＜0【考点】不等式的性质．【分析】根据不等式的性质，即可解答．【解答】解：A、∵m＞n＞0，∴01，故本选项错误；B、∵m＞n＞0，∴m﹣n＞0，故本选项错误；C、∵m＞n＞0，∴﹣m＜﹣n，正确；D、∵m＞n＞0，∴m+n＞0，故本选项错误；故选：C．【点评】本题考查了不等式的性质，解决本题的关键是熟记不等式的性质．5．（x﹣3）（2x+1）=2x2+mx+n，则m，n的值分别是（）A．5，﹣3 B．﹣5，3 C．﹣5，﹣3 D．5，3【考点】多项式乘多项式．【分析】根据多项式乘以多项式，即可解答．【解答】解：（x﹣3）（2x+1）=2x2+x﹣6x﹣1=2x2﹣5x﹣3∵（x﹣3）（2x+1）=2x2+mx+n，∴m=﹣5，n=﹣3，故选：C．【点评】本题考查了多项式乘以多项式，解决本题的关键是熟记多项式乘以多项式．6．如图，已知AC∥BD，∠CAE=30°，∠DBE=45°，则∠AEB等于（）A．30°B．45°C．60°D．75°【考点】平行线的性质．【分析】过E作EF∥AC，然后根据平行线的传递性可得EF∥BD，再根据平行线的性质可得∠B=∠2=45°，∠1=∠A=30°，进而可得∠AEB的度数．【解答】解：过E作EF∥AC，∵AC∥BD，∴EF∥BD，∴∠B=∠2=45°，∵AC∥EF，∴∠1=∠A=30°，∴∠AEB=30°+45°=75°，故选：D．【点评】此题主要考查了平行线的性质，关键是掌握两直线平行，内错角相等．7．如图，以下条件能判定GE∥CH的是（）A．∠FEB=∠ECD B．∠AEG=∠DCH C．∠GEC=∠HCF D．∠HCE=∠AEG 【考点】平行线的判定．【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角，被判断平行的两直线是否由“三线八角”而产生的被截直线．【解答】解：∠FEB=∠ECD，∠AEG=∠DCH，∠HCE=∠AEG错误，因为它们不是GE、CH被截得的同位角或内错角；∠GEC=∠HCF正确，因为它们是GE、CH被截得的内错角．故选C．【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．8的解为（）A．x=4 B．x=3 C．x=0 D．无解【考点】解分式方程．【分析】观察可得1﹣x=﹣（x﹣1），所以最简公分母为（x﹣1）．去分母，化为整式方程求解．结果要检验．【解答】解：方程两边乘以（x﹣1），得5﹣（3﹣x）=2（x﹣1），整理得5﹣3+x=2x﹣2，解得x=4．检验得x=4是原方程的解．故选A．【点评】解分式方程时首先要确定最简公分母，去分母，化分式方程为整式方程，求解后进行检验也是必不可少的一步．9．将分式方程1）A．8x+1=0 B．8x﹣3=0 C．x2﹣7x+2=0 D．x2﹣7x﹣2=0【考点】解分式方程．【分析】本题的最简公分母是x（x+1），方程两边都乘最简公分母，可把分式方程转换为整式方程．【解答】解：方程两边都乘x（x+1），得x（x+1）﹣（5x+2）=3x，化简得：x2﹣7x﹣2=0．故选D．【点评】解分式方程的基本思想是“转化思想”，方程两边都乘最简公分母，把分式方程转化为整式方程求解．10．为改善生态环境，某村拟在荒土上种植960棵树，由于青年团的支持，每日比原计划多种20棵，结果提前4天完场任务，原计划每天种植多少棵？设原计划每天种植x棵，下面方程正确的是（）A BC D【考点】由实际问题抽象出分式方程．【分析】设原计划每天植树x棵，现在每天植树（x+20）棵，根据提前4天完成任务列出分式方程，求出分式方程的解，经检验即可得到结果．【解答】解：设原计划每天植树x棵，现在每天植树（x+20）棵，，故选B【点评】此题考查了分式方程的应用，找出题中的等量关系是解本题的关键．二、填空题11．一个正方形的面积是20，通过估算，它的边长在整数4与5之间．【考点】估算无理数的大小；算术平方根．【分析】本题需要先算出4的平方为16与5的平方为25，所以16的算术平方根是4，25的算术平方根是5，进而得出20的算术平方根在4与5之间．【解答】解：∵正方形的面积是20，∴它的边长为20∴它的边长在整数：在4与5之间．故答案为：4，5．【点评】本题主要考查了估算无理数的大小，解题关键是确定无理数的整数部分即可解决问题．12．不等式2﹣x＜2x+5的解集是x＞﹣1．【考点】解一元一次不等式．【分析】移项、合并同类项、系数化为1即可求解．【解答】解：移项，得﹣x﹣2x＜5﹣2，合并同类项，得﹣3x＜3，系数化为1得x＞﹣1．故答案是：x＞﹣1．【点评】本题考查了一元一次不等式的解法，基本操作方法与解一元一次方程基本相同，都有如下步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1．13．分解因式：9x2﹣4y2=（3x+2y）（3x﹣2y）．【考点】因式分解-运用公式法．【分析】本题符合平方差公式的结构特点，利用平方差公式：a2﹣b2=（a+b）（a ﹣b），此题可求．【解答】解：9x2﹣4y2，=（3x）2﹣（2y）2，=（3x+2y）（3x﹣2y）．【点评】本题考查平方差公式的运用，熟记公式是解题的关键．14．当x≠3时，分式【考点】分式有意义的条件．【分析】根据分式有意义的条件：分母不等于0即可求解．【解答】解：根据题意得：x﹣3≠0，解得：x≠3．故答案：≠3．【点评】本题主要考查了分式有意义的条件，是一个基础题目．15．观察下列各式：13=1213+23=3213+23+33=6213+23+33+43=102…猜想13+23+33+…+103=552．【考点】规律型：数字的变化类．【分析】13=1213+23=（1+2）2=3213+23+33=（1+2+3）2=6213+23+33+43=（1+2+3+4）2=10213+23+33+…+103=（1+2+3…+10）2=552．【解答】解：根据数据可分析出规律为从1开始，连续n个数的立方和=（1+2+…+n）2所以13+23+33+…+103=（1+2+3…+10）2=552．【点评】本题的规律为：从1开始，连续n个数的立方和=（1+2+…+n）2．三、解答题16．（2016春•谯城区校级期末）计算（1）|﹣1|（π﹣3）0+2﹣2（2）（a+2b）（a﹣2b）（a2+4b2）【考点】平方差公式；零指数幂；负整数指数幂．【分析】（1）根据绝对值的性质、非零的零次幂等于1，负整数指数幂与正整数指数幂互为倒数，可得答案；（2）根据平方差公式，可得答案．【解答】解：（1）原式1﹣2+1（2）原式=（a2﹣4b2）（a2+4b2）=a4﹣16b4．【点评】本题考查了平方差公式，熟记公式是解题关键，注意分解要彻底．17．（2016春•谯城区校级期末）解方程（1）3（2x﹣1）2﹣27=0（2【考点】解一元二次方程-直接开平方法；解分式方程．【分析】（1）先移项，再方程两边同除以3，直接开平方即可；（2）先去分母，再去括号，整理即可得出x的值．【解答】解：（1）移项，得3（2x﹣1）2=27，两边同除以3，得（2x﹣1）2=9，直接开平方，的2x﹣1=±3，解得x1=2，x2=﹣1；（2）去分母得，x（x+2）﹣（x2﹣4）=1，去括号得x2+2x﹣x2+4=1，整理得，x=检验：当x=x2﹣4=0，∴x=【点评】本题考查了解一元二次方程，解一元二次方程的方法：直接开平方法、配方法、公式法、因式分解法．18．（2009•数解．【考点】一元一次不等式组的整数解．【分析】先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求其非负整数解即可．【解答】解：解不等式（1）得x≥﹣1解不等式（2）得x＜3∴原不等式组的解是﹣1≤x＜3∴不等式组的非负整数解0，1，2．【点评】本题旨在考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．19．（2016春•x+3）中x=3．【考点】分式的化简求值．【分析】原式利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．【解答】解：原式当x=3时，原式【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．20．（2015春•澧县期末）如图，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD．【考点】平行线的性质．【分析】此题要注意由EF∥AD，可得∠2=∠3，由等量代换可得∠1=∠3，可得DG∥BA，根据平行线的性质可得∠BAC+∠AGD=180°，即可求解．【解答】解：∵EF∥AD（已知）∴∠2=∠3（两直线平行，同位角相等）；∵∠1=∠2（已知），∴∠1=∠3（等量代换）；∴DG∥AB（内错角相等，两直线平行）．∴∠BAC+∠AGD=180°（两直线平行，同旁内角互补）．∵∠BAC=70°，∴∠AGD=110°．【点评】此题考查了平行线的性质与判定，解题时要注意数形结合的应用．21．（2013春•唐山期末）李明到离家2.1千米的学校参加初三联欢会，到学校时发现演出道具还放在家中，此时距聚会还有42分钟，于是分立即步行（匀速）回家，在家拿道具用了1分钟，然后骑自行车（匀速）返回学校，已知李明骑自行车的速度是步行速度的3倍，李明骑自行车到学校比他从学校步行到家少用了20分钟．（1）李明步行的速度是多少米/分？（2）李明能否在联欢会开始前赶到学校？【考点】分式方程的应用．【分析】（1）设李明步行的速度是x米/分，根据李明骑自行车到学校比他从学校步行到家少用了20分钟列出方程，即可得出答案；（2）求出李明赶到学校所用的时间，再与42分钟比较，即可得出答案．【解答】解：（1）设李明步行的速度是x米/分，根据题意得：，解得：x=70，经检验x=70是原方程的解；答：李明步行的速度是70米/分；（21=41＜42，∴李明能在联欢会开始前赶到学校．【点评】本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键，注意分式方程要检验．22．（2016春•谯城区校级期末）观察下列各式：，…（1（2）猜想出能表示上述特点的一般规律，用含字母n的等式表示出来（n是正整数）；（3）请用（2…果．【考点】分式的加减法．【分析】（1）根据拆项法，可得答案；（2）根据拆项法，可得规律；（3）根据规律，可得答案．【解答】解：（1（2（3）原式…【点评】本题考查了分式的加减，利用拆项法得出相反数的项是解题关键．。

七年级下学期期末数学试题含答案注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每小题3分，共30分）1 2018年我国货物贸易进出口总值277900亿元人民币，用科学记数法表示这个数为（）A．2779×1012元 B 2779×1012元 C 02779×1013元 D 2779×1013元2．下列运算中，正确的是（）Aa6÷a3=a2 B(-a)6÷(-a)2=-a4 C(a2)3=a6 D(3a2)4=12a83．下列事件中，是随机事件的是（）A．通常温度降到00C以下，纯净水结冰。

B 随意翻到一本书的某页，这页的页码是偶数。

C．我们班里有46个人，必有两个人是同月生的。

D一个不透明的袋中有2个红球和1个白球，它们除了颜色外都相同，从中任意摸出一个球，摸到白球比摸到红球的可能性大。

4．下列运算中，正确的是（）A．a3·a2=a6 B (-a)2·a3=-a5 C-(-a)3=-a3 D [(-a)3]2=a65．下面的图形中，是轴对称图形的是（）6．如图所示,直线AB与CD相交于点O，OE平分∠BOC，若∠BOE=600，则∠AOC的度数为（）A600 B300 C1200 D450 7．如图，已知D是△ABC的BC边的延长线上一点，DF⊥AB，交AB于点F，交AC于点E，∠A=560，∠D=300，则∠ACB的度数为（）A 560B 440C 640D 540 8．如图，△ABC中，∠C=440，∠B=700，AD是BC边上的高，DE∥AC，则∠ADE的度数为（）A460 B560 C440 D36°ABCDEO╮60°第6题AB C DFE第7题B CDE第8题9 有一辆汽车储油45升，从某地出发后，每行驶1千米耗油01升，如果设剩余油量为y （升），行驶的路程为（千米），则y 与的关系式为（ ）A y=45-01B y=45+01 Cy=45- D y=45+ 10 如图，BC ∥EF ，BC=BE ，AB=FB ，∠1=∠2，若∠1=550，则∠C 的度数为（ ）A 250B550C450D350 二、填空题（每小题 3分，共18分） 11 计算：2m 2n ·(m 2+n-1)= 。

最新七年级（下）数学期末考试试题【答案】一、选择题（共10小题，每小题3分，满分30分）1．下列实数中，属于无理数的是（ ）A 、227B 、3.14CD 、0 答案：C考点：无理数的概念。

解析是无限不循环的小数，所以，是无理数。

2．下面调查中，适宜采用全面调查方式的是（ ）A 、调查某批次汽车的抗撞击能力B 、调查市场上某种食品的色素含量是否符合国家标准 C 、了解某班学生的视力情况 D 、调查春节联欢晚会的收视率答案：C考点：统计。

解析：A 、B 、D 的样本容易大，不适宜采用全面调查方式，只有C ，某班学生的数量是有限的，全面调查可行。

3．如图，直线a ∥b ，直角三角形的直角顶点在直线b 上，已知∠1＝48°，则∠2的度数是（ ）A 、42°B 、52°C 、48°D 、58°答案：A考点：两直线平行的性质，平角的概念。

解析：如下图，依题意，有：∠1＋90°＋∠3＝180°，因为∠1＝48°，所以，∠3＝42°，因为a ∥b ，所以，∠2＝∠3＝42°，选A 。

4．若m ＞n ，则下列不等式变形错误的是（ ）A 、m ﹣5＞n ﹣5B 、6m ＞6nC 、﹣3m ＞﹣3nD 、21m x +＞21n x + 答案：C考点：不等式的性质。

解析：A 、不等式的两边同时减去一个数，不等号方向不改变，故正确；B 、不等式的两边同时乘以一个正数6，不等号方向不改变，故正确；C 、不等式的两边同时乘以一个负数，不等号方向要改变，故错误；D 、不等式的两边同时除以一个正数（2x ＋1），不等号方向不改变，故正确；选C 。

5．方程组3759y x x y =+⎧⎨+=⎩的解是（ ） A 、1272x y ⎧=⎪⎪⎨⎪=⎪⎩ B 、1252x y ⎧=-⎪⎪⎨⎪=⎪⎩ C 、41x y =-⎧⎨=-⎩ D 、21x y =⎧⎨=-⎩ 答案：B考点：二元一次方程组。

2018学年第二学期期末考试七年级数学试卷题 号 一 二 三 四 总 分 得 分一、选择题（本大题共6题，每题2分，共12分）1. 下列实数中，有理数是 （ ） （A ）0.2525525552……（相邻的两个“2”之间每次增加一个“5”）； （B ）π3-； （C ）8； （D ）722． 2. 若三角形的两边长分别为3和6，则第三边的长不可能是（ ） （A ）3； （B ） 4； （C ）5； （D ）6.3. 如图1，能推断AD//BC 的是 （ ） （A ） 43∠=∠； （B ）； （C ） 345∠=∠+∠ ； （D ）213∠+∠=∠．4.平面直角坐标系中,将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比 ( )（A ）横坐标不变,纵坐标加3 （B ） 纵坐标不变,横坐标加3 （C ）横坐标不变,纵坐标乘以3 （D ）纵坐标不变,横坐标乘以3 5. 若点()b a P ,到y 轴的距离为2，则 （ ） （A ）2=a ； （B ）2±=a ； （C ）2=b ； （D ） 2±=b . 6．如图2，已知两个三角形全等，那么∠1的度数是 （ ） （A ）72°；（B ）60°； （C ）58°； （D ）50°．24∠=∠学校 班级 姓名 准考证号EDCBA54321（图2）二、填空题（本大题共12题，每题2分，共24分） 7. 827-的立方根等于 . 8. 比较大小：2. 9. ＝ .10．计算：51515÷⨯= ．11. 位于浦东的“中国馆”总建筑面积约为1601000平方米，这个数字保留两个有效数字可写为 平方米.12. 经过点P ()1,3-且垂直于y 轴的直线可表示为直线_________.13．若三角形三个内角的比为2︰3︰4,则这个三角形是 三角形(按角分类)． 14. 如图3，已知∠ABC ，ACB ∠的平分线CD 交AB 于点D ，//DE BC ，且8AC =，如果点E 是边AC 的中点，那么DE 的长为 .15. 如图4，在△ABC 中，︒=∠70A ，如果ABC ∠与ACB ∠的平分线交于点D ，那么BDC ∠＝ 度.16. 如图5，如果AB ∠CD ，∠1 = 30º，∠2 = 130º，那么∠BEC ＝ 度.17．如图6，将Rt △ABC 绕点O 顺时针旋转90º，得到Rt △A ´OB ´，已知点A 的坐标为（4，2），则点A ´的坐标为____________．18．已知三角形ABC 是一个等腰三角形，其中两个内角度数之比为1:4，则这个等腰三角形顶角的度数为 ．三、简答题（本大题共6小题，每小题6分，共36分）ECB ADCB AD图3图421DCBAE图5图619. 计算：()49813310-++ 20. 计算：()()32362+÷+21．计算：()()225252+-- 22．利用幂的性质进行计算：633326⨯÷23. 如图，在直角坐标平面内，点A 的坐标是(0,3)，点B 的坐标是(3,2)-- （1）图中点C 关于x 轴对称的点D 的坐标是 . （2）如果将点B 沿着与x 轴平行的方向向右平移3个单位得到点B '，那么A 、B ' 两点之间的距离是 . （3）求四边形ABCD 的面积yx···24. 说理填空：如图，点E 是DC 的中点，EC=EB ，∠CDA=120°，DF//BE ，且DF 平分∠CDA ，求证：∠BEC 为等边三角形． 解： 因为DF 平分∠CDA （已知）所以∠FDC=21∠________. （ ） 因为∠CDA=120°（已知） 所以∠FDC=______°. 因为DF//BE （已知）所以∠FDC=∠_________.（____________________________________）所以∠BEC = 60°,又因为EC=EB,（已知）所以∠BCE 为等边三角形.（_____________________________）三、解答题（25题8分、26题8分，27题12分，共28分）FBC ED A25. 如图，在ABC△中，点D、E分别在边AB、AC上，CD与BE交于点O，且满足CEB D=，21∠=∠.试说明ABC△是等腰三角形的理由.26．如图，已知AB=CD，点E是AD的中点，EB=EC. 试说明AD//BC的理由.27. 如果一个三角形能用一条直线将其分割出两个等腰三角形，那么我们称这个三角形为“活三角形”，这条直线称为该“活三角形”的“生命线”. （1）小明在研究“活三角形”AB CDE问题时（如图），他发现，在△ABC中，若∠BAC = 3∠C时，这个△ABC一定是“活三角形”.点D在BC 边上一点，联结AD，他猜测：当∠DAC = ∠C时，AD就是这个三角形的“生命线”，请你帮他说明AD是△ABC的“生命线”的理由.（2）如小明研究结果可以总结为：有一个内角是另一个内角的3倍时，该三角形是一个“活三角形”。