当前位置：文档之家 › 第2章 被控过程特性及其数学模型

第2章 被控过程特性及其数学模型

  • 格式：ppt
  • 大小：893.00 KB
  • 文档页数：63

下载文档原格式

  / 63

合集下载

第二章 被控对象的数学模型

第二章 被控对象的数学模型

Δh:液位的增量 m
dV dh Q1 Q2 A dt dt
Δu1：阀门1开度增量 m2
ΔQ1＝ Ku• Δu1
Ku：阀门1流量系数 m/s
Q2 A 2gh K h
h R Q2
Rs: 液阻 S/m2 h0+Δ h h0 Q20 Q20+Δ Q2
h dh dh ku u1 A C R dt dt
阶跃响应曲线法 1.阶跃响应曲线法 在对象上人为地加 一瞬变扰动，测定 对象的响应曲线， 然后根据此响应曲 线，推求出对象的 传递函数。
缺点：被控参数的偏 差往往会超出实际生 产所允许的数值。
脉冲响应曲线法
u(t)
u(0)
t
y(t)
y(0)
t
2.脉冲响应曲线法
u(t)：矩形脉冲输入
u(t)
u
T
u1(t) t
过程控制系统
按被控对象特性
组成控制系统
控制方案
选择测量控制仪表
控制系统控制效果的好坏，在很大程度 上取决于对被控对象动态特性了解的程 度。
1.选择输入量与输出量
A.多输入单输出的被控对象
e(t) u(t)
液 位 控 制 器 给 水 控 制 阀
+
给定值 -
蒸 汽 流 量
给 水 压 力
锅炉汽 鼓
液位
液 位 变 送 器
1. 概述
若对于复杂的工艺过程，要求出其数学模 型（微分方程）很困难。复杂对象错综复 杂的相互作用可能会对结果产生估计不到 的影响，即使能用机理法得到数学模型， 但仍希望通过实验测定来验证，可采用实 验和测试方法来求取对象数学模型。 方法： 时域法
频域法 相关统计法

第二章1_被控过程的数学模型-单容多容

第二章1_被控过程的数学模型-单容多容

2.2 采用物理机理方法建模
(1) 单容过程的建模
只有一个存储容量的过程。自衡单容过程和无自衡单容过程。
自衡过程：被控过程在扰动作用下，平衡
状态被破坏后，无需操作人员或仪表的干
预，依靠自身能够恢复平衡的过程。
自衡过程的阶跃响应图
无自衡过程：被控过程在扰动作用下，平衡状 态被破坏后，若无操作人员或仪表的干预，依 靠自身能力不能恢复平衡的过程。 无自衡过程的阶跃响应图
2.1 概述
建立数学模型的方法：

物理机理方法建模
根据过程的内在机理，运用已知的静态和动态的能量（物料）平衡关 系，用数学推理的方法建立数学模型。

实验辨识 （系统辨识和参数估计法）
根据过程输入、输出的实验测试数据，通过辨识和参数估计建立过程 的数学模型。

混合法
首先通过机理分析确定过程模型的结构形式，然后利用实验测试数据 来确定模型中各参数的大小。
则系统特性可用下列微分方程式来描述：
2.1 概述
a n c ( n ) (t ) a n1c ( n1) (t ) a1c(t ) a0 c(t ) bm r ( m) (t ) bm1r ( m1) (t ) b1r (t ) b0 r (t )
式中 an , an1 ,, a1 , a0 及 bm , bm1 ,, b1 , b0 分别为与系统 结构和参数有关的常系数。它们与系统的特性有关， 一般需要通过系统的内部机理分析或大量的实验数 据处理才能得到。
2.1 概述
(b) 传递函数 复数域模型包括系统传递函数和结构图，传递函数不 仅可以表征系统的动态特性，而且可以用来研究系统的结 构或参数变化对系统性能的影响。 线性定常系统的传递函数定义为零初始条件下，输出 量（响应函数）的拉普拉斯变换与输入量（输入函数）的 拉普拉斯变换之比。拉普拉斯变换为：

3第二章 过程特性及其数学模型

3第二章 过程特性及其数学模型
假定Q1的变化量用ΔQ1表示，h的变化量用Δh表示。在一定的ΔQ1下， h的变化情况如图2-12所示。
图2-12 水槽液位的变化曲线
在重新达到稳定状态后，一定的ΔQ1对应着一定的Δh值， 令K等于Δh与ΔQ1之比，用数学关系式表示，即
h K Q1
或
h KQ1
h K Q1
或
周 次：第 2周，第 3 次课
教学内容：
第二章 过程特性及其数学模型：第一节 化工
过程的特点及其描述方法，第二节 对象数学模 型的建立，第三节 描述对象特性的参数
教学目的要求 ：
了解化工过程的特点及其描述方法，了解机理建 模和实验建模；掌握表征被控对象特性的三个参 数——放大系数K、时间常数T、滞后时间τ。
2．矩形脉冲法
当对象处于稳定工况下，在时间 t0 突然加一阶跃干扰， 幅值为A，到t1时突然除去阶跃干扰，这时测得的输出量y随 时间的变化规律，称为对象的矩形脉冲特性，而这种形式的 干扰称为矩形脉冲干扰，如图2-9所示。
图2-9 矩形脉冲特性曲线
用矩形脉冲干扰来测取对象特性时，由于加在对象上的 干扰，经过一段时间后即被除去，因此干扰的幅值可取得比 较大，以提高实验精度，对象的输出量又不致于长时间地偏 离给定值，因而对正常生产影响较小。目前，这种方法也是 测取对象动态特性的常用方法之一。 除了应用阶跃干扰与矩形脉冲干扰作为实验测取对象 动态特性的输入信号型式外，还可以采用矩形脉冲波和正 弦信号 ( 分别图团 2-10与图 2-11) 等来测取对象的动态特性， 分别称为矩形脉冲波法与频率特性法。
（4）新型控制方案及控制算法的确定 在用计算机构成一些新型控制系统时，往往离不开被 控对象的数学模型。 (5) 计算机仿真与过程培训系统 利用开发的数学模型和系统仿真技术，使操作人员有 可能在计算机上对各种控制策略进行定量的比较与评定， 有可能在计算机上仿效实际的操作，从而高速、安全、低 成本地培训工程技术人员和操作工人，有可能制定大型设 备启动和停车的操作方案。 (6)设计工业过程的故障检测与诊断系统 利用开发的数学模型可以及时发现工业过程中控制系 统的故障及其原因，并能提供正确的解决途径。

第2章 被控对象的数学模型CAI

第2章 被控对象的数学模型CAI

2.2 对象数学模型的建立
假设两只贮槽的截面积都是A，则有： 假设两只贮槽的截面积都是 ，则有： (Q1−Q12)dt=Adh1 (Q12−Q2)dt=Adh2 改写式（ 改写式（2-18）和式（2-19） ）和式（ ）
dh1 1 = (Q1 − Q12 ) dt A
(2-18) (2-19)
由式（ 由式（2-21）解得 ）
d 2 h2 dh2 AR1 AR2 + ( AR1 + AR2 ) + h2 = R2 Q1 （2-25） 2 ） dt dt 改写成 d 2 h2 dh2 T1T2 + (T1 + T2 ) + h2 = KQ1 （2-26） ） dt dt 式中， 第一只贮槽的时间常数； 式中，T1=AR1—第一只贮槽的时间常数；T2=AR2—第二只 第一只贮槽的时间常数 第二只 贮槽的时间常数； 整个对象的放大系数。 贮槽的时间常数；K=R2—整个对象的放大系数。 整个对象的放大系数 这是描述串联贮槽对象特性的一个二阶常系数微分方程， 这是描述串联贮槽对象特性的一个二阶常系数微分方程， 说明串联贮槽对象是一个二阶对象。 说明串联贮槽对象是一个二阶对象。
第2章 被控对象的数学模型 章
2.1 被控对象的特点及其描述方法 2.2 对象数学模型的建立 2.3 描述对象的特性参数
第2章 被控对象的数学模型 章
2.1 对象的特点及其描述方法
1．数学模型 ．
♦自动控制系统由被控对象、测量变送装置、控 自动控制系统由被控对象、测量变送装置、 制器和执行器组成， 制器和执行器组成，系统的控制质量与组成系统的 每一个环节的特性都有着密切关系。被控对象特性 每一个环节的特性都有着密切关系。被控对象特性 对控制质量影响最大。 对控制质量影响最大。 ♦自动控制系统的设计过程： 自动控制系统的设计过程： 设计过程 了解对象特性及其内部规律 根据工艺对控制 质量的要求 设计合理的控制系统 选择合适的 被控变量和操纵变量 选用合适的测量元件及控 自动控制系统。 制器 自动控制系统。

第二章 被控对象的数学模型

第二章 被控对象的数学模型
或表示为 式中
Ty' (t ) y(t ) Kx(t ) a1 1 T K a0 a0
第二节
对象数学模型的建立
一、建模目的 1 控制系统的方案设计
2
3 4
控制系统的调试和控制器参数的确定
制定工业过程操作优化方案 新型控制方案及控制算法的确定
5
6
建立计算机仿真与过程培训系统
设计工业过程的故障检测与诊断系统
在允许的范围内，多数化工对象可忽略输入项的导数 项，因此可表示为：
an y ( n) (t ) an1 y ( n1) (t ) a1 y' (t ) a0 y(t ) x(t )
一个对象如果可以用一个一阶微分方程式描述其特 性（通常称一阶对象）则可表示为：
a1 y' (t ) a0 y(t ) x(t )
在出水阀开度不变的情况下，随着ｈ的变化，Ｑ２也会变 化。ｈ越大，静压力越大，Ｑ２也会越大
如果Ｑ２变化量很微小，可近似认为Ｑ２与h成正比，与出水阀的阻 力系数RS成反比, 用式子表示为
h Q2 RS
将（2）式代入（1） 式，得
整理后得 令
( 2) (3) ( 4) (5) ( 6) (7 )
h (Q1 )dt Adh RS dh ARS h RS Q1 dt 时间常数 T ARS K RS
L 0 v
从测量方面看，由于测量点选择不当、测量元件安装不合适等 原因也会造成传递滞后。下图为一个蒸汽直接加热器。输入量 蒸汽量；输出量 出口管道的溶液温度，测温点离槽的距离为 Ｌ
例子
相对于蒸汽流量变化的时刻，实际测得的溶液温度Ｔ要经过 时间τｏ后才开始变化
下图为有、无纯滞后的一阶阶跃响应曲线。X为输入量，y(t) 为无纯滞后时的输出量， yτ (t)为有纯滞后时的输出量

2 被控过程的数学模型

2 被控过程的数学模型

第二章被控过程的数学模型¾过程建模的基本概念¾单容过程的建模¾多容过程的建模¾广义对象特性参数及其对过渡过程影响第一节过程建模的基本概念数学模型的作用设计过程控制系统，整定调节器参数 指导生产工艺及其设备的设计与操作 对被控过程进行仿真研究建立过程数学模型的方法机理建模辨识建模过程对象的特性自衡过程过程在扰动作用下，其平衡状态被破坏后，不需操作人员或仪表的干预，依靠其自身重新恢复平衡的过程。

无自衡过程过程在扰动作用下，其平衡状态被破坏后，在没有操作人员或仪表的干预下，依靠其自身能力不能重新恢复平衡的过程。

o K 对控制品质的影响主要反映在静态，愈大，操作变量对被控变量的影响愈灵敏，对干扰的补偿能力越强，有利于克服干扰，减小余差。

o K f K 对控制品质的影响也反映在静态，反映了扰动对被控变量影响的灵敏程度，愈大，影响显著，余差也越大。

f K f K 所以，设计控制系统时应合理选择操作变量，使较大，较小，系统具有很强的抗干扰能力。

但也不能太大，否则过于灵敏，过程不易控制，难以达到稳定。

o K o K 放大系数K及其影响时间常数T及其影响定义：在阶跃输入作用下，对象的输出保持以初始速度变化而达到最终稳态值所需要的时间，反映了响应速度的快慢。

对于干扰通道，则时间常数越大，干扰对被控变量影响越迟钝，易克服干扰而获得较高的控制质量。

f T 对于控制通道，若时间常数太大，则响应速度慢，控制作用不及时，易引起较大超调，过渡过程时间长。

反之，则控制质量易保证。

但时间常数过小，也易引起振荡，使系统稳定性降低。

o Tτ纯滞后时间及其影响实际对象由于多容量的存在会使响应速度变慢，特别是初始响应大大延迟，在动态特性上可近似为纯滞后。

控制通道的存在对控制不利，要隔时间后才有作用，将使被控量超调增大，控制质量恶化，因此必须尽量减少和避免滞后的影响。

o τo τo τ的影响不同于，滞后使干扰作用被推迟了时间进入系统，对过渡过程影响不大。

第2章被控过程的数学模型.

第2章被控过程的数学模型.

21
对于上述水槽而言，在起始稳定平衡工况下， 有 H H0 ， Qi 0 Qo 0 。在流出侧负载阀开度不变的情 况下，当进水阀开度发生阶跃变化 时，若进水流量 和出水流量的变化量分别为 Qi Qi Qi 0 , Qo Qo Qo 0 则在任何时刻液位的变化 H H H o 均满足下述物 料平衡方程：
9
1．建立数学模型的目的
在过程控制中，建立被控对象数学模型的目的主要有以下几 种： (l) 设计过程控制系统和整定控制器的参数 (2) 控制器参数的整定和系统的调试 (3) 利用数学模型进行仿真研究 (4) 进行工业过程优化 另外，设计工业过程的故障检测与诊断系统、制订大型设 备启动和停车的操作方案和设计工业过程运行人员培训系统， 等等都也需要被控过程的数学模型。
d H 1 1 (Qi Qo ) (Qi Qo ) dt F F
(2-7)
22
当进水阀前后压差不变时，Qi 与 成正比关系， 即
Qi k
(2-8)
对于流出侧的负载阀，其流量与水槽的水位高度有 关，即 (2-9) Q k H
o
式(2-9)是一个非线性方程。这个非线性给下一步的 分析带来很大的困难，应该在条件允许的情况下尽量避 免。如果水位始终保持在其稳态值附近很小的范围内变 化，那就可以将上式加以线性化。
18
2．测试法建模
测试法一般只用于建立输入输出模型。它是根据工业过程 的输入和输出的实测数据进行某种数学处理后得到的模型。它 的主要特点是把被研究的工业过程视为一个黑匣子，完全从外 特性上测试和描述它的动态性质，因此不需要深入掌握其内部 机理。然而，这并不意味着可以对内部机理毫无所知。为了有 效地进行这种动态特性测试，仍然有必要对过程内部的机理有 明确的定性了解，例如究竟有哪些主要因素在起作用，它们之 间的因果关系如何等等。 用测试法建模一般比用机理法建模要简单和省力，尤其是

第二章 过程特性及其数学模型

第二章 过程特性及其数学模型
A—水槽截面积 将dV代入
0 h h2
t1
t
(Q1 Q2 )dt Adh
h1
t1
t
h Q2 Rs
Rs—阀的阻力
h )dt Adh 代入上式 (Q1 Rs
整理得
dh ARs h Rs Q1 dt
K=Rs
一阶常系数微分 方程
令：T=ARs 所以
dh T h KQ1 dt
t dh T h KQ1 解微分方程得 h KQ (1 e T ) 1 dt
当对象受到阶跃变化Q1=A 输出h是如何变化的。如图
Q1
A
0
h KA(1 e )
当t →∞时， h(∞)=KA 或 K=h(∞)/A

t T
t
h
h(∞) 0
t1
t
放大系数，是对象的静态参数
储槽的阶跃响应曲线
三、对象动态特性的研究方法 1.理论分析 根据系统工艺实际过程的数质量关系，分析计算 输入量与输出量之间的关系。
2.实验研究 需要在实际系统或实验系统中，通过一组输入 ,来 考察输出的跟随变化规律—反映输入与输出关系 的经验曲线和经验函数关系。
第二节 对象数学模型的建立
一、 机理建模法 机理法建摸就是根据生产过程的内在机理，写出各 种有关平衡方程式。如物料平衡方程式、能量平衡 1 方程式等。 1、一阶对象（单容对象） 举例 如图所示为一液体储槽对象 其静态方程
11．已知一个对象特性是具有纯滞后的一阶特性， 其时间常数为5，放大系数为10，纯滞后时间为2 ，试写出描述该对象特性的一阶微分方程式。
无滞后 有滞后 一阶微分方程式：
dy(t 2) 5 y(t 2) 10 x(t ) dt

第02章 被控过程的数学模型2018

第02章 被控过程的数学模型2018

实际上，储槽底面积，即液容类似于电容。电容越大，
相同的电流变化（增量）造成的电压改变越小；同样，
储槽底面积越大，相同流量的改变造成的液位改变越
小。
单容对象——参数含义
阻力R：凡是物质或能量的转移，都要克服阻力，阻力
的大小决定于不同的势头和流率。 种类有：电阻、热 阻、气阻、流(液)阻。 电路中把RC定义为时间常数T，T越大，瞬态响应时间
被控 参数
A
A：水箱截面积 流出量
或
dh （Q1 Q2） dt
（ 1）
dh 1 （Q1 Q2） dt A
2.2.1 单容过程建模
1 .单容储液箱液位过程Ⅰ－自衡过程
单容液位过程稳态时 ：
Q1 Q10、 Q2 Q20、 h h0， Q10 Q20
μ：阀门1的开度 流入量
越长。液位对象也有这个特点，T越大，流量改变后液
位H达到新的稳态的过渡过程时间也越长。
2.2.1 单容过程建模
1 .单容储液箱液位过程Ⅰ－自衡过程 K0 H (s) 单容过程方框图： W (s)
0
Q1 ( s )
T0 s 1
（ 8）
d h C (Q1 Q2 ) dt
Q2 h R2
（ 5）
2.2.1 单容过程建模
1 .单容储液箱液位过程Ⅰ－自衡过程
Q1 h d h A R2 dt
（ 5）
整理可得：
AR2 d h h Q1R2 dt
d h h K0 Q1 dt
（ 6）
μ：阀门1的开度
流入量
令：
T0 AR （ , K0 R2 2 CR2）
1 .单容储液箱液位过程Ⅰ－自衡过程

第二章 过程特性及其数学模型(修改

第二章 过程特性及其数学模型(修改

被控 对象
自动化 装置



第一节 化工过程的特点及其描述方法
自动控制的效果取决于被控对象（内因）和控 制装置（外因）两个方面。 ‫ ۝‬外因只有通过内因起作用，内因是最终效果的 决定因素。 设计调节控制系统的前提是：正确掌握工艺系 统调节作用（输入）与调节结果（输出）之间 的关系——对象的特性。 所谓研究对象特性就是用数学的方法描述对象 输入量与输出量之间的关系
对象特性的实验 建模
输入量 阶跃信号 脉冲信号 伪随机信号 ……
——在被控对象上人为加入输入量，记录表征对象
特性的输出量随时间的变化规律。
被控对象
输出量 表格数据 响应曲线 ……
系统辨识 对象模型
对象特性的实验建模
加测试信号前，要求系统尽可能保持稳定状态，否则会影响测
试结果；
输入量/输出量的起始时间是相同的，起始时间是输入量的加
干扰通道
被控变量
通道输出之和
控制通道
第二节 对象数学模型的建立
建模的方法：机理建模、实验建模、混合建模
机理建模——根据物料、能量平衡、化学反应、传热传质等基本 方程，从理论上来推导出输入与输出的数学关系式，建 立数学模型。 由于工业对象往往都非常复杂，物理、化学过程的机理一般 不能被完全了解，而且线性的并不多，再加上分布元件参数 （即参数是时间与位置的函数）较多，一般很难完全掌握系统 内部的精确关系式。另外，在机理建模过程中，往往还需要引 入恰当的简化、假设、近似、非线性的线性化处理等，而有时 这些假设与实际生产有较大差距，因而机理建模仅适用于部分 相对简单的系统。
第二节 对象数学模型的建立
实验建模——在所要研究的对象上，人为的施加一个输入作用， 然后用仪表记录表征对象特性的物理量随时间变化的规 律，得到一系列实验数据或曲线。这些数据或曲线就可 以用来表示对象特性。 这种应用对象输入输出的实测数据来决定其模型的方法，通 常称为系统辨识。其主要特点是把被研究的对象视为一个黑箱 子，不管其内部机理如何，完全从外部特性上来测试和描述对 象的动态特性。有时，为进一步分析对象特性，可对这些数据 或曲线进行处理，使其转化为描述对象特性的解析表达式。

第二章被控对象的数学模型

第二章被控对象的数学模型

第二章被控对象的数学模型第二章被控对象的数学模型1(什么是被控对象特性?什么是被控对象的数学模型?研究被控对象特性有什么重要意义?答:被控对象持性是指被控对象输入与输出之间的关系。

即当被控对象的输入量发生变化时，对象的输出且是如何变化、变化的快慢程度以及最终变化的数值等。

对象的输入量有控制作用和扰动作用，输出量是被控变量。

因此，讨论对象特性就要分别讨论控制作用通过控制通道对被控变量的影响，和扰动作用通过扰动通道对被控变量的影响。

定量地表达对象输入输出关系的数学表达式、称为该对象的数学模型。

在生产过程中，存在着各种各样的被控对象。

这些对象的持性各不相同。

有的较易操作，工艺变量能够控制得比较平稳，有的却很难操作，工艺变量容易产生大幅度波动，只要稍不谨慎就会越出工艺允许的范围，轻则影响生产，重则造成事故。

只有充分了解和熟悉对象特性，才能使工艺生产在最佳状态下运行。

因此，在控制系统设计时、首先必须充分了解被控对象的特性，掌握它们的内在规律，才能选择合适的被控变量、操纵变量，合适的测量元件和控制器(选择合理的控制器参数，设计合乎工艺要求的控制系统。

特别在设计新型的控制系统时。

例如前馈控制、解偶控制、自适应控制、计算机最优控制等，更需要考虑被控对象特性。

2(简述建立对象的数学模型的两种主要方法。

答:一是机理分析法。

机理分析法是通过对对象内部运动机理的分析，根据对象中物理或化学变化的规律(比如三大守恒定律等)、在忽略一些次要因素或做出一些近似处理后推导出的对象特性方程。

通过这种方法得到的数学模型称之为机理模型，它们的表现形式往往是微分方程或代数方程。

二是实验测取法。

实验测取法是在所要研究的对象上，人为施加一定的输入作用，然后，用仪器测取并记录表征对象特性的物理量随时间变化的规律，即得到一系列实验数据或实验曲线。

然后对这些数据或曲线进行必要的数据处理，求取对象的特性参数，进而得到对象的数学模型。

3(描述简单对象特性的参数有哪些?各有何物理意义?答:描述对象特性的参数分别是放大系数K、时间常数T、滞后时间τ。

过程控制第2章被控过程的数学模型

过程控制第2章被控过程的数学模型
第一段：t=0～a，
y1 t y t
第二段：t=a～2a，
y1 2a y 2a y1 a
2.3.3 由阶跃响应曲线确定过程的数学模型
1.一阶无时延过程 2.二阶无时延过程
K0 W0 ( s) T0s+1
K0 W 0 ( s) T1s 1T2 s 1
t
⑴合理选择阶跃信号值。 ⑵在输入信号前，被控对象必须处于相对稳定的运行 状态。 ⑶实验时应在相同试验条件重复做几次测试，需获得 两次以上比较接近的测试数据，以减少扰动的影响。 ⑷在实验时应在阶跃信号作正、反方向变化时分别测 取其响应曲线，以求取过程的真实特性。 特点：简单、易实现，测试精度不高，对生产有影响。
当对象受到阶跃输入作用 后，被控参数如果保持初 始速度变化，达到新的稳 定值所需的时间。
h
h′
h
t
t
K 0 Q1 d h dt t 0 T
K 0 Q1 h t t T
'
实验求取T：当t=T，
h t K 0 Q1 1 e 1 0.632 K 0 Q1 0.632h
0
t 浓度
0
t
2.容量时延C
H 2( s ) K0 W 0( s ) e cs Q1(s) T 0 s 1
由于物料或能量的传递需要通过一定的阻力而引起的。
K0 Y ( s) W0 ( s) e s X ( s) T0 s 1
意义： ①表示对象的惰性； ②大时控制困难。 ③是一动态特性参数。
K0 T1 ( s) R W0 ( s) Q1 (s) RCs 1 T0s+1
例2—3 自衡特性： 当输入量发生变化破坏了被控过程的平衡而引起输 出量变化时，在没有人为干预的情况下，被控过程 自身能重新恢复平衡的特性，叫做自衡特性。 具有自衡特性的被控过程称为自衡被控过程， 无自衡特性的被控过程称为无自衡被控过程。

第二章 被控过程的数学模型

第二章 被控过程的数学模型
曲线能形 直观、 象、直观、 完全描述 被控过程 的动态特 性。
图2-8 响应曲线
第33页 页
过程控制仪表及装置
实验测试注意事项： 实验测试注意事项： 合理选择阶跃信号值。 合理选择阶跃信号值 。 一般取阶跃信 号值为正常输入信号的5 15％左右； 号值为正常输入信号的5～15％左右； 在输入阶跃信号前， 在输入阶跃信号前 ， 被控过程必须处 于相对稳定的工作状态； 于相对稳定的工作状态； 相同的测试条件下重复做几次， 相同的测试条件下重复做几次 ，减少 干扰的影响； 干扰的影响； 由于过程的非线性， 由于过程的非线性 ， 应在阶跃信号作 正 、 反方向变化时分别测取其响应曲 以求取过程的真实特性。 线，以求取过程的真实特性。
d 2∆h2 d∆h2 T1T2 + (T1 + T2 ) + ∆h2 = R3∆Q1 2 dt dt
第24页 页
过程控制仪表及装置
进行拉氏变换，并分解因式， 进行拉氏变换，并分解因式，得： 双容过程的数学模型为： 双容过程的数学模型为：
K R3 H 2 (s ) W (s ) = = = Q1 (s ) (T1 s + 1)(T2 s + 1) (T1 s + 1)(T2 s + 1)
对上式进行拉氏变换， 对上式进行拉氏变换，传递函数形式为
1 1 W0 (s) = = Cs Ta s
具有纯时延 τ 0 时，其传递函数为
1 −τ 0 s Wo ( s ) = e Ta s
第20页 页
过程控制仪表及装置
2.2.2 多容过程的建模 多容过程------ 被控过程往往是由多个 多容过程 ------被控过程往往是由多个 -----容积和阻力件构成。 容积和阻力件构成 。 可分为有自平衡能 力和无自平衡能力两类。 力和无自平衡能力两类。

第二章 被控过程的数学模型

第二章 被控过程的数学模型

后才反应出来。 要经过路程 l 后才反应出来。
℃
0 t
τ
0
纯滞后时间
l τ0 = v
℃
v ——水的流速； 水的流速；
0 有些对象容量滞后与 纯滞后同时存在，很难严格 纯滞后同时存在， Δh2 （∞） 区分。常把两者合起来， 区分。常把两者合起来，统 称为滞后时间τ 0
τ0
t
τ=τ
o
+τc
τ0 τc
单回路控制系统框图
过程通道： 过程通道：
被控过程输入量与输出量之间的信号联系
控制通道： 控制通道：
控制作用与被控量之间的信号联系
扰动通道： 扰动通道：
扰动作用与被控量之间的信号联系
建立过程数学模型的基本方法： 建立过程数学模型的基本方法：
解析法： 解析法： 又称为机理演绎法 ，根据过程的内在机理，运用已知 根据过程的内在机理， 的静态和动态物料（能量）平衡关系， 的静态和动态物料（能量）平衡关系，用数学推理的方法建 立过程的数学模型。 立过程的数学模型。 实验辨识法： 实验辨识法： 又称为系统辨识与参数估计法。该法是根据过程输入、 又称为系统辨识与参数估计法。该法是根据过程输入、输 出的实验测试数据， 出的实验测试数据，通过过程辨识和参数估计建立过程的数学 模型。 模型。 混合法: 混合法: 即用上述两种方法的结合建立过程的数学模型。 即用上述两种方法的结合建立过程的数学模型。首先通 过机理分析确定过程模型的结构形式， 过机理分析确定过程模型的结构形式，然后利用实验测试数据 来确定模型中各参数的大小
其中： 其中：
T = R 2 C 为被控过程的时间常数
K = R2
为被控过程的放大系数
Hs +1 1 2

第二章 过程(对象)特性及其数学模型

第二章 过程(对象)特性及其数学模型

由于
消去i 消去i 图8-3 RC电路 电路
de0 RC + e0 = ei dt
de0 T + e0 = ei dt
或
T = RC
20
第二节 机理建模
二、积分对象
化学工业出版社
当对象的输出参数与输入参数对时间的积分成比例关系时， 当对象的输出参数与输入参数对时间的积分成比例关系时， 积分对象。 称为积分对象 称为积分对象。9Βιβλιοθήκη 第一节 数学模型及描述方法
1.微分方程 1.微分方程 对于线性的集中参数对象
化学工业出版社
通常可用常系数线性微分方程式来描述，如果以x（t ） 通常可用常系数线性微分方程式来描述， 如果以 （ 表示输入量， （ 表示输出量， 表示输入量，y（t）表示输出量，则对象特性可用下列微分 方程式来描述
F (s ) = ∫ f (t )e − st dt
0
∞
（8-7）
12
第一节 数学模型及描述方法
化学工业出版社
运用拉氏变换的线性性质与微分性质, (8运用拉氏变换的线性性质与微分性质,对式 (8-1) 两端分别取拉氏变换, 两端分别取拉氏变换,则得
an s nY (s ) + an −1s n −1Y (s ) + ⋅ ⋅ ⋅ + a1sY (s ) + a0Y (s ) = bm s m X (s ) + bm −1s m −1 X (s ) + ⋅ ⋅ ⋅ + b1sX (s ) + b0 X (s )
TsY (s ) + Y (s ) = KX (s )
化学工业出版社
因此一阶对象的传递函数形式为
K G (s ) = Ts + 1

第2章 被控过程特性及其数学模型

第2章 被控过程特性及其数学模型
3）常见的数学模型结构
k0 k 0 e 0 s k0 G ( s) ; G ( s) ; G ( s) T0 s 1 T0 s 1 (T1 s 1)(T2 s 1) k 0 e 0 s G ( s) (T1 s 1)(T2 s 1) 1 e 0 s 1 G ( s) ; G ( s) ; G( s) T0 s T0 s T1 s(T2 s 1) 1 G ( s) e 0 s T1 s(T2 s 1)
（2）在相同的条件下，应重复做几次试验；
（3）分别作阶跃输入信号为正反方向两种变化情况下的测试试 验；
（二） 实验测试法建模
（4）一次试验后，应使被控过程恢复到原来工况并稳定一定时间，
再作第二次试验； （5）输入阶跃变化既不能太大，也不能太小，一般取正常输入信号
最大幅值的5～15％。
（二） 实验测试法建模
③系统总的传递函数 Go (s) K 2
s
二 、被控过程的数学模型
被控过程的数学模型是指被控过程的输出变量 与输入变量之间的数学描述或指被控过程的状态变 量与输入变量、输出变量之间的数学描述。 输入变量： 控制作用、 干扰作用 输出变量： 被控变量 控制作用到输出变量的信号联系为控制通道 干扰作用到输出变量的信号联系为干扰通道
（一） 机理演绎法建模
自平衡的概念及其实质
所谓有自平衡能力的过程是指被控过程在干扰作用下，原有 的平衡状态被打破后，在没有人或控制装置的干预下，自身可 以恢复到新的平衡状态，这种过程称为有自平衡能力的过程（ 如例1），否则称为无自平衡能力的过程（如例2）。 具有自平衡能力的过程其输出和输入之间有负反馈，如例1的 方块图
3．自衡的振荡过程
c(t) c(∞)

6.第二章 被控对象的数学模型

6.第二章 被控对象的数学模型

第二章被控对象的数学模型主要研究内容：⏹化工过程的特点及其描述方法⏹对象数学模型的建立（建模）•建模目的•机理建模•实验建模⏹描述对象特性的参数•放大系数Κ•时间常数Τ•滞后时间τ第二章被控对象的数学模型⏹控制效果取决于控制对象（内因）和控制系统（外因）两个方面。

۝外因只有通过内因起作用，内因是最终效果的决定因素。

⏹设计控制系统的前提是：正确掌握工艺系统、控制作用（输入）与控制结果（输出）之间的关系——对象的特性。

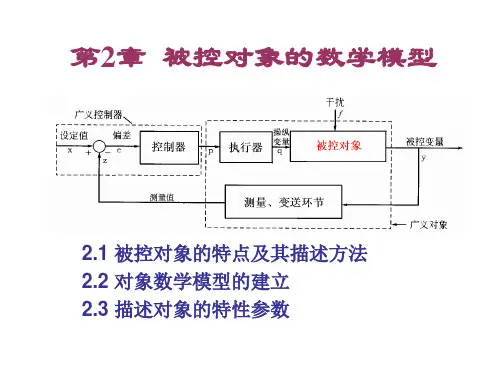
自动控制系统是由被控对象、测量变送装置、控制器和执行器组成。

研究对象的特性，就是用数学的方法来描述出对象输入量与输出量之间的关系。

建立对象特性的数学描述就称为建立对象的数学模型（建模）。

第二章被控对象的数学模型对象的数学模型分为静态数学模型和动态数学模型。

静态数学模型动态数学模型基础特例对象在稳定时(静态)输入与输出关系；在输入量改变以后输出量跟随变化的规律；•比较与区别：动态数学模型是更精确的模型，静态数学模型是动态数学模型在对象达到平衡时的特例。

一、化工对象的特点⏹被控对象常见种类：换热器、锅炉、精馏塔、化学反应器、贮液槽罐、加热炉等⏹1. 对控制质量影响程度相差大（内因决定外因）；⏹2. 类型繁多，特性相差悬殊；⏹3. 非线性、分布参数较多；第二章被控对象的数学模型§2.1 化工对象的特点及其描述方法二、对象特性定义⏹对象特性，即过程特性：指被控过程输入量发生变化时，过程输出量的变化规律。

⏹输入量：干扰作用、控制作用。

⏹输出量：被控参数。

⏹数学建模——就是用数学的方法来描述出对象输入量与输出量之间的关系。

⏹通道：被控过程的输入量与输出量间的信号联系。

⏹控制通道-----操纵变量至被控变量的信号联系.⏹扰动通道-----扰动变量至被控变量的信号联系.被控变量(输出量)扰动变量（输入量）操纵变量（输入量）数学模型的描述方法：1. 非参量模型：用曲线、数据图表表示的系统输入与输出量之间的关系；非参量模型可以通过记录实验结果来得到，有时也可以通过计算来得到，它的特点是形象、清晰，比较容易看出其定性的特征。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

K e -s (Ts 1) n
过程的纯滞后时间
2.1 被控过程的特性
（2）无自衡的非振荡过程
无自衡：在原平衡状态出现干
扰时，当没有外加任何控制作 用时，被控过程不能重新到达 新的平衡状态
无自衡非振荡：阶跃输入信号 作用下，输出响应曲线会没有 振荡地从一个稳态一直上升或 下降，不能达到新的稳态
第二章 被控过程特性及其数学模型
主要内容
2.1 被控过程的特性 2.2被控过程的数学模型 2.3解析法建立过程的数学模型
2.4实验辨识法建立过程的数学模型
2.1 被控过程的特性
（1）自衡的非振荡过程
自衡：在原平衡状态出现干扰 时，无需外加任何控制作用，
被控过程能够自发地趋于新的 平衡状态。
自衡非振荡：阶跃输入信号作 用下，输出响应曲线能没有振 荡地从一个稳态趋向于另一个 稳态.
实验辨识法
实验辨识法-------根据过程输入、输出的实验测试数据， 通过过程辨识和参数估计得出数学模型。 过程辨识-----根据测试数据确定模型结构（包括形式、方程 阶次及时滞等）。
参数估计-----在已定模型结构的基础上，再由测试数据确定 模型的参数。
混合法
（1）对被控过程中机理比较清楚的部分采用机理演绎
单容自衡过程可以采用一阶惯性环节加以描述。
2.3 解析法建立过程数学模型—单容过程
单容过程传递函数的结构方框图
水箱的输入量/输出量之 间的动态平衡关系 Q1 (s)
1 cs
Q2 (s)
H(s)
1 R2
阀2的静压力关系
2.3 解析法建立过程数学模型—单容过程
推广1：考虑输入液体体积流量为Q0 当进水阀1的开度产生变化后，需流经长度为l 的管道才能
T0=R2A K0=R2
C=A
τ0与l有关
2.3 解析法建立过程数学模型—单容过程
无时延自衡
Q1
有纯时延自衡
Q0
O
O
t
h
t
h
O
O t
0
t
2.3 解析法建立过程数学模型—单容过程
推广2：考虑输出液体体积流量为Q2通过泵来调节
液位高度变化时，出口处静压力不会对泵产生影响，Q2不变。
解 根据动态物料平衡关系: q1 q2 A dh 定量泵导致: q2 0
单位时间内进入被控过程的物料或能量,减去单位时 间内从被控过程流出的物料或能量,等于被控过程内 物料或能量的变化率。 单位时间内进入被控过程的物料或能量,等于单位时间内, 从被控过程流出的物料或能量 不足：需要有足够和可靠的验前知识，否则，推导的结果就可能出现失真。 优点：在过程控制系统没有建立之前就先推导出数学模型，对于系统事先设 计和方案论证十分有利。
Q1 (s)
1 H1(s) 1 Q2 (s) c1s R2
Q3 (s)
1 c2 s
H2(s)
1 R3
阀3的静 压力关系
2.3 解析法建立过程数学模型—多容过程
分析： 1）两个具有负实根的惯性环节串联， 即ξ=1过阻尼，响应不振荡。 2）双容过程在两个槽之间存在液体 流通阻力，延缓了h2的变化，导致响应 过程一开始较慢，较单容过程时延大。
②参量形式模型：曲线、表格等
2.2 被控过程的数学模型—方法
白箱方法-----解析法（机理演绎法）
黑箱方法-----实验辨识法（系统辨识与参数估计方法）
灰箱方法-----解析法与实验辨识相结合的混合方法
解析法
解析法-------根据被控过程的内在机理，运用已知的静态和动态 物料平衡、能量平衡等关系，用数学推理的方法求取被控过程 的数学模型。
过程的时间常数
2.1 被控过程的特性
（3）自衡的振荡过程 自衡振荡：阶跃输入信号作用下， 输出响应曲线呈现衰减振荡特性， 最终被控过程趋于新的稳态值。
K Go ( s ) 2 2 e -s , (0 1) T s 2Ts 1
2.1 被控过程的特性
（4）具有反向特性的过程 阶跃输入信号作用下，被控过程的输出先降后升或先升后降，即过 程响应曲线在开始的一段时间内变化方向与以后的变化方向相反，
2.3 解析法建立过程数学模型—单容过程
单容过程-------只有一个贮蓄容量的过程。
自衡：被控过程在扰动作 用下，平衡状态被破坏后， 不需要操作人员或仪表的 干预，依靠自身能够恢复 平衡。 无自衡：平衡状态被 破坏后，被控量会不 断变化下去，不能再 平衡。
2.3 解析法建立过程数学模型—单容过程
例2-1 某水箱系统如图所示。
输入液体体积流量Q1通过阀门1的开度来改变。 输入液体体积流量Q2通过阀门2的开度来改变。 液位高度h为被控量。 要求：试列写h与Q1之间的数学表达式。
2.3 解析法建立过程数学模型—单容过程
解 根据动态物料平衡关系:
dh q1 q2 dt
单位时间内水箱内液体流入 量与流出量之差 水箱截 面积
进入水箱，使液位发生变化。
假设流经长度为l的管道所需时间为τ0，得出具有纯时延的
单容过程的微分方程和传递函数分别为
dh h R2 q0 (t - 0 ) dt K 0 0 s H (s) R2 0 s G( s) e e Q1 ( s) R2 As 1 T0 s 1 R2 A
冷水量对水位的直接影响 正向积分特性
反向特性 冷水量影响水中气泡量，使 水位发生变化 反向惯性特性
2.2 被控过程的数学模型—概念
被控过程的数学模型
----过程的输入变量与输出变量之间的定量关系。
作用于过程的控制 作用和干扰作用
过程的被控变量
控制通道：控制作用到输出变量的信号联系。 干扰通道：干扰作用到输出变量的信号联系。
h q2 R2
阀门阻力，即流量增加 1m2/s时的液位升高量
2.3 解析法建立过程数学模型—单容过程
综合上述两类关系：
dh q1 q2 A dt h q2 R2 dh h R2 q1 dt
经整理得到单容液位过程的微分方程增量表示
R2 A
拉氏变换，得到传递函数形式
水箱内液体 容量变化率
表示为增量形式有:
dh q1 q2 A dt
q1 , q2 , h —偏离某平衡状态 q10 , q20 , h0 的增量
静态时： q1 q2
dh 0 dt
2.3 解析法建立过程数学模型—单容过程
根据压力关系:
假定q2与h 近似成线性正比关系，与阀门2处的液阻R2 成反比 关系，则
差分方程形式: a n y(k n) a1 y(k 1) y(k ) bm u(k m d ) b1u(k 1 d ) e( K )
b0 b1 z 1 bm z m d 脉冲传递函数: y (k ) z u (k ) 1 n 1 a1 z a n z
2.1 被控过程的特性
（1）自衡的非振荡过程
过程的静态增益 （或放大系数）
具有纯滞后的一阶惯性环节 G ( s) K e s o 过程的时间常数
Ts 1
具有纯滞后的二阶非振荡环节 Go ( s)
K e -s (T1s 1)(T2 s 1)
具有纯滞后的高阶非振荡环节 G ( s ) o
拐 3）随着相连接容器的增加，过程时 点 间延迟越长。
4）模型简化：采用单容过程近似。
G( s) R3 H 2 (s) e 0 s Q1 ( s ) T0 s 1
2.3 解析法建立过程数学模型—多容过程
推广1：考虑n个水槽（容器）依次分离式连接 类推出多容过程（n个）的传递函数
K0 G( s) (T1s 1)(T2 s 1) (Tn s 1)
G( s) R3 e l s (T1s 1)(T2 s 1)
h2
h2(∞)
R3 e ( 0 l ) s (T0 s 1)
O
τ0 + τ1
T0
t
2.3 解析法建立过程数学模型—多容过程
推广3：考虑输出液体体积流量为Q3通过泵来调节 ------水槽1的液位高度变化，会对Q2产生影响。
过程的放大系数 K=R3
获得双容液位过程的传递函数为
G( s) R3 Q2 ( s) H 2 ( s) 1 Q1 ( s) Q2 ( s) T1s 1 T2 s 1
双容自衡过程可以采用二阶环节加以描述。
2.3 解析法建立过程数学模型—多容过程
双容过程数学模型的结构方框图
水槽1的输入量/ 输出量之间的动 态平衡关系 阀2的静压 力关系 水槽2的输入量/ 输出量之间的动 态平衡关系
过程的总 放大系数 各单容过程的 时间常数
若各个容器的容量系数相同，各阀门的液阻也相同，则
K0 G(s) (T0 s 1) n
T1 T2 Tn T0
注：多容过程模型简化过程与双容过程简化为单容过程方法类似。
2.3 解析法建立过程数学模型—多容过程
推广2：考虑两水槽之间的管道长度 当阀2的开度变化后，需流经长度为l 的管道才能进入贮 罐2，使液位h2发生变化。 假设流经管道所需时间为τ1，则具有纯时延多容过程传 递函数为
----水槽2的液位高度变化，不会对Q3产生影响。
解 根据多容过程类推关系: G1 (s)
Q2 ( s) 1 1 Q1 ( s) T1s 1 R2C1s 1 H 2 (s) 1 1 Q2 ( s ) T2 s c2 s
2.3 解析法建立过程数学模型—多容过程
解 根据动态平衡关系，有
dh1 dt dh2 水槽2 q2 q3 C2 dt
水槽1 q1 q2 C1 阀2
h1 q2 R2