当前位置：文档之家 › 二阶系统的时域分析.ppt

二阶系统的时域分析.ppt

  • 格式：ppt
  • 大小：941.50 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

第3讲 二阶系统的时域分析

第3讲 二阶系统的时域分析

18
三、典型二阶系统的动态过程分析
（一）衰减振荡瞬态过程 (0 1)：欠阻尼
s 1, 2 ζω n jωn 1 ζ
2
ζω n jωd
c (t ) 1 Fra biblioteke ζωn t 1 ζ 2
sin(ωd t β ) ,
t 0
⒈ 上升时间 t r ：根据定义，当 t t r时，c(tr ) 1 。
3
s1, 2 n n 1
2
⒊ 当 1 时，特征方程有一对相等的实根，两个极点位于S平 面负实轴上，系统时间响应无振荡，称为临界阻尼系统，系统 的阶跃响应为非振荡过程。 ⒋ 当 1 时，特征方程有一对不等的实根，两个极点位于S 平面负实轴上，系统时间响应无振荡，称为过阻尼系统，系统 的阶跃响应为非振荡过程。 以上 1 属于非振荡情况
于是有：
tr d
ωd ωn 1 ζ 2

n
n

j n 1 2 j d
n

称为阻尼角
j n 1 2
cos
可见，当阻尼比一定时，系统的响应速度与自然频率成正比； 而当阻尼振荡频率一定时，阻尼比越小，上升时间越短。
2 n 1 C ( s) ( s) R( s) 2 2 s 2 n s n s
2 其中, 由特征方程 s 2 2 n s n 0
可求得两个特征根（即闭环极点）
s1, 2 n n 2 1
6
[分析]：
s1, 2 n n 1
s n n 1 2 2 2 2 s s 2 n s n s 2 n s n

线性系统的时域分析法二阶系统

线性系统的时域分析法二阶系统
实验法具有直观性和可验证性的优点，适用于各种类型的二阶系统。但是，实验法需要实际设备和实 验条件，成本较高。
04
二阶系统的稳定性分析稳定性定义平衡状态
线性系统在平衡状态下的输出称为平衡状态输出。
稳定性
如果一个系统的平衡状态输出对于所有初始条件和输入都是稳定的，则称该系统是稳定 的。
稳定性判据
劳斯-赫尔维茨判据
数值法
数值法是通过数值计算来求解二阶系 统的方法。它通过将时间轴离散化， 将微分方程转化为差分方程，然后使 用迭代或直接计算的方法求解。
数值法具有简单易行和适用性广的优 点，适用于各种类型的二阶系统。但 是，对于某些特殊类型的系统，数值 法可能存在精度和稳定性问题。
实验法
实验法是通过实际实验来测试二阶系统的方法。它通过在系统中输入激励信号，然后测量系统的输出 响应，从而得到系统的性能参数。
线性系统的时域分析 法二阶系统
目录
CONTENTS
• 线性系统的时域分析法概述 • 二阶系统的基本概念 • 二阶系统的时域分析方法 • 二阶系统的稳定性分析 • 二阶系统的性能指标分析 • 二阶系统的应用实例
01
线性系统的时域分
析法概述
定义与特点
定义
时域分析法是一种通过在时间域 内对系统进行直接分析的方法， 用于研究系统的动态性能和响应 特性。
通过计算系统特征方程的根来判断系统 的稳定性。如果所有根都位于复平面的 左半部分，则系统稳定；如果有根位于 右半部分，则系统不稳定。
VS
Nyquist稳定判据
通过绘制系统的开环传递函数的Nyquist 曲线，判断曲线是否不穿越复平面的右半 部分，从而判断系统的稳定性。
稳定性分析方法
直接法

3-3二阶系统的时域分析

3-3二阶系统的时域分析

二阶系统的闭环极点分布
j
特征根： s1, 2 n n 2 1
j
n 1 2
j

n
n 1 2

n

0

n 1 2
0
1
0
n 1 2
0 1
1 0
j
s1 s 2 n 0
1
1
C1 C2 C3 L C1e S t C2 e S t C3 ( s s1 ) ( s s2 ) s
1
1 2
其中
C1
n2
( s1 s2 ) s1
; C2
n2
( s1 s2 ) s2
; C3 1
而s1，s2是ζ和ωn的函数，显然c(t)只与ζ ，ωn有关，即ζ ，ωn决
第三章 时域分析法
第三节 二阶系统时域分析
第三节 二阶系统的时域分析
项目
教学目的
内容
掌握二阶系统的数学模型和时域响应的特点。 能够计算欠阻尼时域性能指标。
欠阻尼时域性能指标的计算。阻尼系数和自 然频率对系输出的影响。
教学重点
教学难点 阻尼 系数 和自然频率 对系统输出 的影响 。 及 其 处 理 MATLAB作图、对比、总结。
①
环节；
比例+微分（引入零点）：在前向通路中串一个PD控制
② 采用测速反馈控制。 3) PD控制与测速反馈控制两种方案比较 （见下页附表）
附表： PD控制与测速反馈控制两种方案比较
性能指标
PD控制
方
案
测速反馈控制 增 大 降 低
阻尼比 自然频率 开环增益 稳态误差 超调量 性能 适用场合

自动控制理论时域分析2--二阶系统

自动控制理论时域分析2--二阶系统
c ( tP) c ( ) M 100 % P c ( )
4．调整时间 t s（又称过渡过程时间） ：响应曲线达到并 保持与稳态值之差在预定的差值△内（又叫误差带 ）所 需要的时间。一般△取±2%或±5%。
二、二阶系统的动态响应性能指标 （1）峰值时间 t P
因为
c (t ) 1 e nt 1
2
sin( d t )
t n p d
dc ( t ) dt
d p
0
ttp
e sin( t ) e cos( t ) 0
t n p n d p
整理得：
tg ( ) dtp
12

p t p 0, ,2 ,3
n

0 Re
s1
s2
0
Re
s2
s1
0
Re
0
Re
s2
(a) 0 1 (b) 1 (c) 1 (d) 0
特征根为：共扼复数 特征根为：
相等实数
不等实数
共扼虚数
1．欠阻尼情况 :
( 0 1 )
2
s n 1 1 , 2 n
s j 1 , 2 n d
c ( t) 1 cos t n
c (t )
( 0)
(t 0)
2
1
0
t
这是一条等幅振荡曲线。
( 0)
c (t )
1
c (t ) r (t )
2
1
1
c (t )
0
t
0
t
( 0 1 )
1
r (t )

自动控制理论时域分析2-二阶系统

自动控制理论时域分析2-二阶系统

案例二：二阶系统稳定性分析与改善
稳定性分析方法
介绍时域分析法中的劳斯判据、赫尔维茨判据等方法，用于判断二 阶系统的稳定性。
改善稳定性措施
探讨通过改变系统参数、引入附加环节等措施来改善二阶系统的稳 定性。
仿真验证
利用MATLAB/Simulink等仿真工具对改善前后的二阶系统进行建模 和仿真，验证改善措施的有效性。
CHAPTER
二阶线性常微分方程
二阶线性常微分方程的一般形式： $Tfrac{d^2y}{dt^2} + frac{dy}{dt} + Ky = F(t)$
方程的解由输入信号 $F(t)$ 和系统初 始条件共同决定
其中，$T$ 为时间常数，$K$ 为放大 系数，$F(t)$ 为输入信号
二阶系统的传递函数
二阶系统稳定性的判定方法
二阶系统的稳定性可以通 过判断其阻尼比和自然频 率来确定。
当阻尼比大于1时，系统是 过阻尼的，输出会缓慢地趋 近于零，系统是稳定的。
当阻尼比等于1时，系统是临 界阻尼的，输出会以最快的速 度趋近于零，系统也是稳定的 。
当阻尼比等于0时，系统是无 阻尼的，输出会呈现等幅振荡 的形式，系统是不稳定的。
谢谢
THANKS
二阶系统的基本概念
01
二阶系统是指具有两个独立状态变量的线性定常系统，其数学 模型可用二阶常微分方程描述。
02
二阶系统具有广泛的代表性，许多实际系统可简化为二阶系统
进行分析。
二阶系统的性能指标包括阻尼比、自然频率、峰值时间、超调
03
量等，这些指标对于评价系统性能具有重要意义。
02 二阶系统的数学模型
当阻尼比小于1时，系统是欠 阻尼的，输出会呈现振荡衰减 的趋势，系统仍然是稳定的。

自动控制原理第三章 二阶系统PPT

自动控制原理第三章 二阶系统PPT

tr t p
ts
t
第一节 系统的时域性能指标
2．抗扰性能指标
（1）动态降落 如果控制系统在稳态运行中受到扰 c(t) △cmax ±5% 动作用 , 经历一段动态过程后又能达到新 系 统 输 出 C∞1 的 最大降落 的稳态。可用抗扰性能指标来描述系统 值。 的抗扰性能. 0 t tν （2）恢复时间 系统输出恢复到与误差带范围所需的 根据系统在负载扰动之后的典型过 时间。 度过程定义抗扰性能指标: 返回
n n
ωdtr+β=0,π,2π…
第三节 二阶系统性能分析
2. 峰值时间tp -ζ ω t t -ωne e ω sin( ωdtp+β)] 2 ζ cos( ω t + β ) [ nβ 1ζ c(t)=1Sin( ω t+ ) = 1-ζ2 d p d 2
n p
n
1-ζ =0 dc(tp) =0 则 根据定义有 -ζ ω n sin(ωdtp+β)=0 1-ζ2 cos(ωdtp+β) dt
第三节 二阶系统性能分析
1. ζ >1 过阻尼
两个不相等 S1.2 = - ζ ω n ±ω n ζ 2 -1 的负实数根 A1 A2 A3 ωn C(s)= = + S S-S1 S-S2 S(S-S1)(S-S2) 拉氏反变换
c(t)=A1+A2es1t+A3es2t
系统输出随时间单调上升，无振荡和 超调，输出响应最终趋于稳态值1。
c(t)=t-T+Te-t/T
可知: 系统输入信号导数的输出响应，等 于该输入信号输出响应的导数；根据一种 典型信号的响应，就可推知于其它。
第二节 一阶系统性能分析

自动控制原理3.3~3.4 二阶系统时域分析

自动控制原理3.3~3.4 二阶系统时域分析

闭环特征方程： D( s ) s 2 2 s 2 0 n n 闭环特征根： s1, 2 n n
2
1
二、二阶系统单位阶跃响应
单位阶跃输入r(t)=1(t)时，其二阶系统的输出的拉氏变换为
2 2 n n 1 C ( s ) ( s ) R( s ) 2 2 s 2 n s n s s( s s1 )(s s2 )
e
(ζ ζ 2 1 ) n t
ζ 2 1 ) n t
c(t ) 1
1
2 ζ 2 1 (ζ ζ 2 1) 1 (ζ e 2 ζ 2 1 (ζ ζ 2 1)
e
(ζ ζ 2 1 ) n t
ζ 2 1 ) n t
c(t)
1
0 t
单调上升过程
2.0 1.8 1.6 1.4 1.2 c(t) 1.0 0.8 0.6 0.4 0.2 0
=0
0.4 0.5 0.6 0.7 0.8
0.1 0.2 0.3
1.0 2.0
1
2
3
4
5
• 在0<<1, 越小，超调量越大，平稳性越差，调节时间ts长； • =0.7，调节时间短，而超调量%<5%，平稳性也好，故称 ζ=0.7为最佳阻尼比。工程希望=0.4～0.8为宜； •在≥1 , 越大，系统响应速度慢，调节时间ts也长。
例题：设角度随动系统如图所示，T=0.1为伺服电机时间常数， 若要求系统的单位阶跃响应无超调，且调节时间ts≤1s，问K应 取多大？此时上升时间等于多少？
Θi(s)
_
K s(Ts 1)
Θo(s)
解：闭环传递函数为
K K K /T s (Ts 1) (s) 2 2 K Ts s K s s / T K / T 1 s (Ts 1)

阶电路和二阶电路的时域分析.outpu

阶电路和二阶电路的时域分析.outpu
特性
全响应是零输入响应和零状态响应的叠加。在响应过程中，电压或电流既包含瞬态分量（ 由初始状态引起），也包含稳态分量（由外部激励引起）。
分析方法
通过求解电路的一阶微分方程，可以得到全响应的数学表达式。根据初始条件、激励源的 形式和电路参数，可以确定响应的具体形式。同时，可以利用叠加原理将全响应分解为零 输入响应和零状态响应两部分进行分析。
冲激响应
01
定义
冲激响应是指电路在冲激信号作用下的响应。冲激信号是 一种在某一时刻瞬间出现并立即消失的信号，具有极短的 持续时间和极大的幅度。
02 03
性质
冲激响应具有瞬态性质，表现为电路在冲激信号作用下的 瞬间反应。冲激响应的幅度和持续时间取决于电路的结构 和参数。
分析方法
对于一阶电路和二阶电路，可以通过求解电路微分方程得 到冲激响应的解析表达式。同时，也可以利用电路仿真软 件进行数值分析。在实际应用中，常常利用卷积定理将冲 激响应与输入信号进行卷积运算，从而得到电路的零状态 响应。
两者之间的关系
联系
阶跃响应和冲激响应都是描述电路在 特定信号作用下的时域行为。它们都 可以通过求解电路微分方程得到，并 且可以利用电路仿真软件进行数值分 析。
区别
阶跃响应描述的是电路在阶跃信号作 用下的响应，而冲激响应描述的是电 路在冲激信号作用下的响应。阶跃信 号是一种持续存在的信号，而冲激信 号是一种瞬间出现的信号。因此，阶 跃响应和冲激响应在时域上具有不同 的特性。
探索新的数学工具和分析方法， 提高时域分析的精度和效率。
结合实际应用需求，研究电路的时域 响应特性和稳定性问题，为电路设计 提供更加全面和深入的理论指导。
THANKS
感谢您的观看
有广泛的适用性。

3.3.2 二阶系统的时域分析

3.3.2 二阶系统的时域分析



2.动态性能指标
1.上升时间tr
当t t r时，y t r 1 y t r 1 即 e wntr 1 e wntr 1
2 2
e wntr 1
2
sin wn 1 2 t r 1


sin wn 1 2 t r 0 0 sin wn 1 2 t r 0 wn 1 2 t r k tr




t r为满足此式的最小正数
wn 1 2 t r

wn 1 2

wd
tr

wn 1 2


wd
上升时间和什么有关系？
增大自然频率 wn或减小阻尼比
均能减小tr，从而加快系统的初始 响应速度。
请大家回去思考一个问题 二阶系统初始斜率为多少？
2
闭环特征根
s1, 2 wn jwn 1 2
1 当输入信号为单位阶跃 函数时 Rs s 2 wn 1 Y s Rs GB s 2 2 s 2wn s wn s s wn 1 s s w 2 w 1 2 n n
三.欠阻尼二阶系统的动态性能指标 1.欠阻尼下根的分布
jwn
jwn 1 2
0
s w jw 1
1, 2 n n
2
s1

w jw
n
d
s2
wn
jwn 1 2
衰减系数 wn 是闭环极点到虚轴的距 离。 振荡频率wd wd wn 1 2 是闭环极点到实轴 的距离。无阻尼振荡频 率wn是闭环极点到原点 的距离。若直线 os1与负实轴的夹角为 ，则阻尼 比就等于的余弦，即 cos 。因此就是欠阻尼 二阶系统单位阶跃响应 的初相角。

二阶系统时域分析

二阶系统时域分析

线性系统的时域分析法>>二阶系统的时域分析
特征方程为：
s2
2 n s
2 n
0
特征根为：s1,2 n n 2 1 ，注意：当 不同时，（极点）
有不同的形式，其阶跃响应的形式也不同。它的阶跃响应有振
荡和非振荡两种情况。
1) 当时 0，特征方程有一对共轭的虚根，称为零(无)阻尼
系统，系统的阶跃响应为持续的等幅振荡。
Δ=2的精确曲线 Δ=5的精确曲线
10
Δ=5的近似曲线 Δ=2的近似曲线
8
6
4
0.304
0.43
2
0.19
0.23
0.38
0.53
0.69 0.78
0
0.1 0.2 0.3 0.4 0.5 0.6
0.7 0.8 0.9
1
线性系统的时域分析法>>二阶系统的时域分析
由分析知，在 0.4 ~ 0.8 之间，调节时间和超调量都较小。工程 上常取 1 0.707 作为设计依据，称为最佳阻尼常数。
由于t p出现在第一次峰值时间，取n=1，有：
25
20
15
10
tp
5
tr
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
线性系统的时域分析法>>二阶系统的时域分析
3)最大超调量 %：
将峰值时间 t p n
1 2
代入 c(t)得c(t p) cmax
cmax c(t p ) 1 e ntp (cosd t p
s1,2 jn
s1,2 n jn 1 2

自动控制原理第三章(2)

自动控制原理第三章(2)
n
dh(t ) t>0 >0 dt dh(t ) t = ∞ h(t ) = 1 =0 dt
二阶
小结： 小结：过、临界阻尼无振荡。 临界阻尼无振荡。
三、欠阻尼二阶系统 0 < ζ < 1
1 r(t)=1(t) R ( s ) = 单位阶跃响应： 单位阶跃响应： s 2 ωn 1 β C ( s) = 2 ⋅ 2 s + 2ζωn s + ωn s −ζωn s + ζωn ζωn 1 = − − 2 2 2 2 s ( s + ζωn ) + ωd ( s + ζωn ) + ωd
dh(t ) 1 =− [−ζωn e −ζωnt sin(ωd t + β ) + e −ζωnt cos(ωd t + β )ωd ] 2 dt 1− ζ
jωn 1 −−ζωn
β
= jωd
− jωn 1 − ζ 2
= − jωd
π π ∴t p = = ωd ωn 1 − ζ 2
h(t ) = 1 −
e
− ζωnt
σ %
p
tt
1− ζ 2
sin(ωd t + β )
∴ζωn sin(ωd t + β ) − ωd cos(ωd t + β ) = 0
1− ζ ωd ∴ tan(ωd t + β ) = = = tan β ζωn ζ ∴ωd t = 0, π , 2π ⋯
2
1− ζ
2
包络线进入误差带的时间近似
ts =
3
ζωn
(±5%)或
4
ζωn
(±2%)
讨论： (1)ωn一定,ζ 讨论：

33二阶系统解析

33二阶系统解析

➢单位阶跃响应的变化率为：
dc(t) dt
n2tent
dc(t) 0 dt t0
dc(t) 0 dt t0
dc(t) 0 dt t
表明临界阻尼系统的阶跃响应是单调上升的。
➢ 单位阶跃响应变化率最大的时刻：
d 2h(t) dt 2
dh(t ) max
e2 nt n
(1
nt )
0
dt
解得 t 1/。n ➢ 整个暂态过程中，临界阻尼系统阶跃响应都是单调 增长的没有超调。如以达到稳态值的95%所经历的时 间做为调整时间，则
（1）平稳性
主要由最大超调量 % 和振荡次数 表征。 增大， %减 小，平稳性变好；若 不变，n 增大，d 增大， 增大，平
稳性变差。
（2）快速性
主大要，由则上tr升越时长间，t快r 速和性调越节差时；间当ts
表征。当 n 一定时，
越短，快速性越好。而对于ts ，则与 和n
一定时， 越
n 越大，则 tr
讨论: (1)欠阻尼情况下，二阶系统的单位阶跃响应是衰减的 正弦振荡曲线。衰减速度取决于特征根实部的绝对值
ζωn的大小，振荡角频率是特征根虚部的绝对值，即有 阻尼自振角频率ωd，
d n 1 2
(2)振荡周期为
Td
2 d
n
2 1 2
(3)ζ越大，振幅衰减越快，振荡周期越长（频率越低）。
(4)上升时间tr的计算：
dc(t)
( 2 1)n
e( 2 1)nt
dt 2 2 1( 2 1)
( 2 1)n
e( 2 1)nt
2 2 1( 2 1)
dc(t ) dt
0
0
t 0 t 0

二阶系统的时域分析

二阶系统的时域分析

d
1 2 (s n )2 d2
进行拉式反变换后可得：
c(t) 1
ent
1 2
sin(d t
)
结论：
1、稳态分量为1；
arctan 1 2
2、暂态分量在 一定时，其衰减程度(速度的快慢) 由 中n 的 决n定( 越大n ，衰减程度越快)。
0.5,n 分别为1、2、3、4时的响应曲线。
n 1, 2,3, 4时的响应曲线。
2
3
4
n 一定时，随 的增大，系统的响应速度变慢。
4,n 1, 2,3 时的响应曲线。
n 3 n 2 n 1
一定时，随n 的增大，系统的响应速度变快。
小结：二阶系统中 和n的作用
1) 0时，系统输出不稳定。
2) 0 1时，系统输出有超调，且 决定了超调量 的大小, 和 n 共同决定了系统的响应速度。
c(t)输出为一发散形式的曲线。
2,n 1时的阶跃响应：
2) 0 (零阻尼)
C(s)
R(s)(s)
1 s
n2 s2 n2
1 s
s2
s
n2
c(t) 1 cosnt
c(t)输出为一条在0和2之间振荡的曲线。
n 1
n 2
3) 0 1 (欠阻尼)
C(s)
1 s
(s
s n n )2 d2
1 (R1C1
R2C2
R1C2 )s
1
机械力学系统的传递函数
1 (s) ms2 fs k
举例
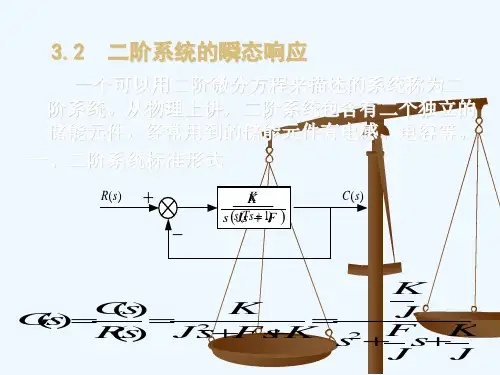
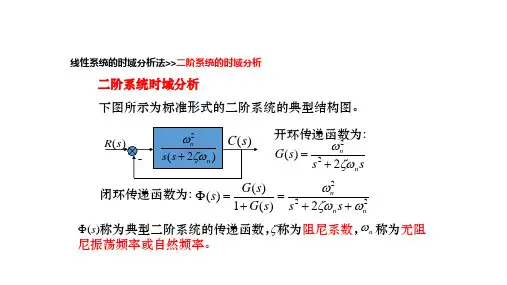
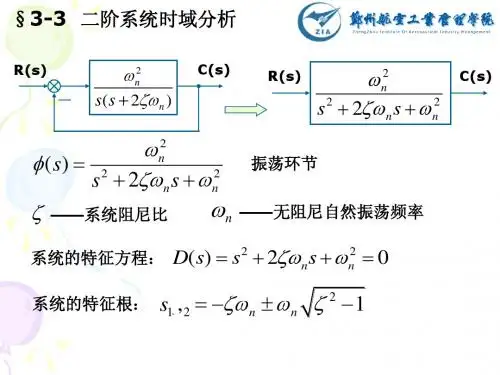
一般形式的二阶微分方程 化为传函的标准形式
(s)
s2
n2 2n s
n2
a0
d 2c(t) dt 2
a1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

d ds
[C
(s
)(
s
n
)
2
]s
n
1
2 [C(s) (s n )2 ]sn n
C(t) 1 ent ntent 1 ent (1 nt) (t 0)
j [s]
s1s2
n o
1
C(t) 1
1 是输出响应的单调和振荡过程的分界，通
常称为临界阻尼状态。
o
2020/3/29
3-3二阶系统的时域分析
况，故称为阻尼系数。
2020/3/29
3-3二阶系统的时域分析
10
3.二阶系统的性能指标(1)－上升时间
根据定义，当 t tr时，c(tr ) 1。 令 c(t) 1 et sin (dt+ ) =1
sin
c(t) 1 et sin (dt+ ) , t 0 sin
e t sin (d t+ ) 0 sin
T1 T2
n
T2
1
n
h(t)= 1 -(1临+ω界n阻t)尼0je-ωnt
0＜0＜ξ＜ξ＜1 1 S1,2= -ξ ωn ±jj ωn√1-ξξ2 ＝0
jj 0
0
0
e - h(t)=
ξ＝1 0 1
2020/3/2√91-ξ2
-ξωSnt欠1s,2i阻n=(尼ω±d3t-j3+二ωβ阶n)系统的时域分析
为阻尼振荡圆频率。
2020/3/29
3-3二阶系统的时域分析
1 2 是振荡频率。称 d
5
2.二阶系统的单位阶跃响应(4)-过阻尼
极点：s1,2 n n 2 1
阶跃响应：c(t) 1
n
e e s1t
s2t
()
(t 0)
2 2 1 s1 s2
稳态分量为1，瞬态分量包含两个衰减指数 项，曲线单调上升。
s n
n
]
s (s n )2 (n 1 2 )2 (s n )2 (n 1 2 )2
拉氏反变换:
1
s
s
[ (s
)2
d2
c(t) 1 et (cosd
(s
t d
)2 d2 sin dt)
*
d d
]
1
e t
sin
[sin
cos(d
t)
cos
sin(d
t)]
2020/3/29
1 et
sin(dt ) 3-3s二in阶系统的时域分析
4
2.二阶系统的单位阶跃响应(3)-欠阻尼
C(t)
超 调 量
1.0
误差带
c(t) 1 et sin(dt ) ,t 0 sin
稳态误差 (t )
o
t
上升时间
峰值时间
调节时间
控制系统性能指标
极点的负实部 n 决定了指数衰减的快慢，虚部 d n
t 临界阻尼响应
7
2.二阶系统的单位阶跃响应(6)-无阻尼
极点：s1,2 jn
将 0代入
C(t) 1 ent (cos d t
1
2
sin d t)
阶跃响应：c(t) 1 cosnt
C(t)
系统的输出响应是无阻尼的等幅振荡过程，
其振荡频率为 n
1
o
2020/3/29
3-3二阶系统的时域分析
ωn2 s2+2ξωns+ωn2
2020/3/29
3-3二阶系统的时域分析
3
2.二阶系统的单位阶跃响应(2)-欠阻尼 j [s]
极点: s1,2 n jn 1 2＝ jd
s1
n 1 2
n
阶跃响应:
C(s)
1 s s2
n2 2ns n2
1 s
s2
s 2n 2ns n2
n o s2
1 [
3－3 二阶系统的时域分析
2020/3/29
3-3二阶系统的时域分析
1
1.二阶系统的数学模型
开环传递函数:
G(s)
s2
n2 2ns
R(s)
闭环传递函数:
(s)
G(s) 1 G(s)
s2
n2 2ns n2
特征方程： s2 2ns n2 0
特征根： s1,2 n n 2 1
n2
C(s)
令 c(t) e t sin(d t ) e td cos(d t ) 0
tan (dt+ )=tan
dt k k=0,1L
取k=1,得
t p d
j [s]
s1
n 1 2
n
n o
s2 0 1
2020/3/29
3-3二阶系统的时域分析
12
3.二阶系统的性能指标(3)－超调量
零阻尼j
h(t)= 1 cos0ωnt 9
2.二阶系统的单位阶跃响应(8)
C(t)
2
1.8 1.6
1.4
1.2
1
0.8
0.6 0.4 0.2
0 0
246
nt
8 10 12
可以看出：随着 的增加，c(t)将从无衰减的周期运动变为有衰减的正弦运动，
当
时1 c(t)呈现单调上升运动(无振荡)。可见 反映实际系统的阻尼情
C(t)
超 调 量
1.0
误差带
sin (dt+ )=0
稳态误差 (t )
dt =k k=0,1,2L
o
上升时间
t
解2020得/3/2：9 tr
d
峰值时间
3-3二阶系统的时域分析 调节时间
11
控制系统性能指标
3.二阶系统的性能指标(2)－峰值时间
当 t tp 时， c&(tp ) 0
c(t) 1 et sin (dt+ ) , t 0 sin
s2 s1
j
[s]
0
1
过阻尼时极点分布
C(t)
1
2020/3/29
3-3二阶系统的时域分析
o
t
过阻尼响应 6
2.二阶系统的单位阶跃响应(5)-临界阻尼
极点: s1,2 n
C(s) n2 0 1 2 s(s n )2 s s n (s n )2
0 [C(s) s]s0 11源自{- s(s 2n )
n —自然频率
阻尼比
1
1 0 1
0
2020/3/29
3-3二阶系统的时域分析
2
2.二阶系统的单位阶跃响应(1)
输入： R(s) 1 s
输出： C(s) (s) 1 s
n2
1
s2 2n n2 s
AB C
s s s1 s s2
c(t) L1[C(s)]
Φ(s)=
将峰值时间
tp
d
代入 c(t)得c(tp ) :
c(tp )
1 etp
sin (dtp ) sin
100 90
80
1 e
1 e d
sin ( + )
70
c tan 60
sin
50
40
%
c(t
p ) c() c()
100%
(c(t
p
)
1)
100%
30 20 10
故： % ectan 100%
j
[s]
s1
n
o
s2 0 (a)
(b) t
8
2.二阶系统的单位阶 跃响应(7)
Φ(s)=
ωn2 s2+2ξωns+ωn2
ξ＞ξ＞1 1
- S1,2=
ξω ω√ ±j 1
1
n T2
T1
n ξ2
-
1ξ＝1
0
jj 00
= - hξ＝(t)1
1+
t
t
e = +ξωe = -ω TTS211,过21T1阻尼