当前位置：文档之家 › 3.2 一阶系统的时域分析

3.2 一阶系统的时域分析

  • 格式：pdf
  • 大小：388.33 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

自动控制第三章s讲解

自动控制第三章s讲解


trtp ts
稳态误差
t
振荡系统定义为从零第一次上升到终值所需时间。
峰值时间tp：响应到达第一个峰值所需时间。 调节时间ts：到达并保持在终值 5％误差带内所需的最短时间 超调量%：最大偏离量c(tp)与终值c(∞)之差的百分比，即
% c(t p ) c() 100 %
c()
❖稳态性能：由稳态误差ess描述。
跟踪误差：e(t)=r(t)-c(t)=Tt-T2(1-e-t/T)随时间推 移而增长，直至无穷。因此一阶系统 不能跟踪加速度函数。
线性定常系统的特性
单位脉冲信号 r(t) (t) R(s) 1
单位阶跃信号 r(t) 1 单位斜坡信号 r(t) t
R(s) 1 s
R(s)
1 s2
单位加速度信号 r (t ) t 2 2 R(s) 1 s3
3.1 时间响应性能指标
3.1.1 典型输入信号
典型输入信号
单位阶跃信号、单位斜坡信号、单位脉冲信号、 单位加速度信号、正弦信号。
对应的输出分别被称为 单位阶跃响应 、单位斜坡响应 、单位脉冲响应 、 单位加速度响应。
一．阶跃函数
r(t)
A
0 r(t) A
t0 t0
R(s) A s
o
t
A=1时称为单位阶跃函数, 其数学表达式为
k Ts+1
输入R(s)
1 s2
输出速度 dc(t) 1 et T
dt
位置误差随时间增
单
大,最后为常值T
位
斜
T
坡
响
应
0T
3.2.5 一阶系统的单位加速度响应
无零点的一阶系统 Φ(s) =
k Ts+1
一阶系统

一阶系统

自动控制理论
Automatic Control Theory
1
第2章 要 点
建模,化简
建模:输入—输出模型 微分方程，传递函数
化简： 结构图，信号流图
2
第3章 线性系统的时域分析
分析和设计控制系统的首要工作是建立系统的 数学模型。在获得系统的数学模型后，就可以 采用不同的数学方法去分析系统的性能。
控制系统的主要分析方法 时域分析法 根轨迹分析法 频域（率）分析法 ……
3
第3章 线性系统的时域分析
时域法是一种直接又比较准确的分析方 法，它通过拉氏反变换求出系统输出量 的表达式，提供系统时间响应的全部信 息。
时域分析法得到的结果直观，但其计算 量随系统阶次的升高而急剧增加。
4
第3章 线性系统的时域分析
为了衡量系统的动态性能，同时便于对不同系 统的性能进行比较，通常采用单位阶跃函数作 为测试试验信号。相应地，系统的响应称为单 位阶跃响应。
14
3.1 典型试验信号与系统性能指标
系统性能指标
y(t)
ymax
1.05 y () 1.00 y () 0.95 y() 0.90 y()
0.50y()
方程
.
..
y(0), y(0), y(0), y(n1) (0)
.
..
u(0),u(0),u(0), u(m1) (0)
初始条件
y(t) yt (t) yss (t)
解的结果
12
3.1 典型试验信号与系统性能指标
时域响应的构成
暂态响应（自由分量）和稳态响应（强迫分量 ）
y(t) yt (t) yss (t)
r(t) 1 at 2 2
自动控制原理--一阶系统的时域分析相关知识

自动控制原理--一阶系统的时域分析相关知识


三、 一阶系统的单位脉冲响应
输入信号 r(t) (t) R(s)＝1
c(t)
输出信号 C(s) (s)R(s) 1
1/T
Ts 1
斜率-1/T2
0.368/T 0.135/T
c(t) 1 et /T T
拉氏反变换，得 t k(t) L1[C(s)] L1[ (s)]
0 T 2T 3T 图3.10 一阶系统的单位脉冲响应
• 例3-1：
一阶系统如图所示，试求系统单位阶跃响应的调 节时间ts，如果要求ts=0.1秒，试问系统的反馈 系数应如何调整？
• 例3-2：
G(s) 10
已知某元部件的传递函数为：
0.2s 1
采用图示方法引入负反馈，将调节时间减至原来 的0.1倍，但总放大系数保持不变，试选择KH、 K0的值。
1 et /T (t 0) T
三、 一阶系统的单位脉冲响应特点
• 1）可以用时间常数去度量系统的输出量数字。 • 2）初始斜率为-1/T2 。 • 3) 无超调，稳态误差为零 。
h(t)
超调量
1.0 0.9
延迟时
0.5 间
0.1 0
峰值时间
上升时间 调节时间
误差带 0.02或0.05
稳态误差 (t→∞)
s
输出 C (s) (s) R(s)
1 1 Ts 1 s
1 1 取拉氏反变换，得 s Ts 1
h(t) 1 et /T (t 0)
一阶系统单位阶跃响应是终值为1的单调上升过程。
c(t) c(t) 1 et /T dh(t) 1
1
dt t0 T
0.865
0.632
td 0.69T
一阶反馈系统
假设将一阶系统作为反馈控制系统的对象， 放大器增益可调，系统结构图如图所示。
32一阶系统的时域分析

32一阶系统的时域分析


k(0)=
1 T
h’(0)=1/T
K’(0)=
1
Th2(TT)=0.632h(∞)
h(2T)=0.865h(∞)
响应应
h(3T)=0.95h(∞)
问应
1 、3个图各如何求T？ h(42T、)=调0.节98时2h间(∞ts=)？
3 、r(t)=vt时，?ess=？
4、求导关系
小结: t d 1（t） d 2 t 1t
什么是二阶系统？凡以二阶微分方程作为运动方 程的控制系统，即为二阶系统。 研究二阶系统的意义:
1. 二阶系统的典型应用极为普遍 2. 不少高阶系统的特性在一定条件下可用二阶系 统特性来表征。
本节主要内容： 一、继续讲二阶系统的时域分析中的几种工作状态。 二、二阶系统的性能改善，关键是改变了阻尼比和
ch(t()t=)1=-1e－e-t/T
63.2% 86.5% 95% 98.2% 99.3%
t
0
T
2T 3T 4T 5T
稳态性能指标:
图 3-4指 数 响 应 曲 线
一阶惯性系统的单位阶跃响没有静态误差
ess
lim r (t )
t
h(t)
1
h()
11
0
讨论：动态指标与时间常数T有关，T越小，其响应过
dt
T dc(t) c(t) r(t)
(3-2)
dt
其中，T＝RC为时间常数；取拉氏变换
TsC(s) C(s) R(s)
TsC(s) C(s) R(s)
则一阶系统的传递函数为：
i(t) R
(s) C(s) 1 R(s) Ts 1
(3-3)
r(t)
C c(t)
第3章_时域瞬态响应分析_3.2一阶系统的瞬态响应

第3章_时域瞬态响应分析_3.2一阶系统的瞬态响应


(t ≥ 0)
1 斜率 − 2 T
1 0.368 T
1 − t /T xo (t ) = e T
T
一阶系统三种典型输入信号及响应关系： 一阶系统三种典型输入信号及响应关系：
xi (t ) = t
输 入
xt (t ) = t − T + Te x1 (t ) = 1 − e 1 1 −T t xδ (t ) = e T
x0(t) 1
1/T
xo(t)=1-e-t/T
86.5%
0
63.2%
95.0%
98.2%
T
2T
3T
4T
t
特点 一阶惯性系统总是稳定的，无振荡。 （1）一阶惯性系统总是稳定的，无振荡。 曲线上升到0.632的高度 。 反过来 ， 的高度。 （ 2 ） 经过时间 T ， 曲线上升到 的高度 反过来， 如果用实验的方法测出响应曲线达到0.632的时间 ， 的时间， 如果用实验的方法测出响应曲线达到 的时间 即是惯性环节的时间常数。 即是惯性环节的时间常数。 经过时间3 响应曲线达稳定值的95 95％ （3）经过时间 3T～ 4T，响应曲线达稳定值的95％～ 98％ 可以认为其调整过程已经完成， 98 ％ ， 可以认为其调整过程已经完成 ， 故一般取调 整时间( 整时间(3～4)T。 响应曲线的切线斜率为1/T。 （4）在t＝0处，响应曲线的切线斜率为 。
注意： 该性质只适用于线性定常系统， 注意 ： 该性质只适用于线性定常系统 ， 不适用于 线性时变系统和非线性系统。 线性时变系统和非线性系统。
1 T T = 2− + s s s+ 1 T
单位斜坡响应为 x0 (t ) = t − T + Te
3-2 一阶系统的时域分析

3-2 一阶系统的时域分析


一阶系统结构如图所示， 例: 一阶系统结构如图所示，试求该系统的单位 阶跃响应及调节时间。若要求t 阶跃响应及调节时间。若要求 s<0.1s，试问系 ， 统的反馈系数K 应如何选取？ 统的反馈系数 t应如何选取？
R(s)
－
100
C(s)
s
Κt
解：系统闭环传递函 数为： 数为：
C ( s) 100 Φ(s) = = R( s) s + 100 K t = 1 Kt 1 100 K t 1 Kt = Ts + 1 s +1
瞬态分量 稳态分量
瞬态分量变化规律由传递函数的极点s=－1/T决定 瞬态分量变化规律由传递函数的极点s=－1/T决定 极点s=
c(t ) = 1 − e
t − T
t≥0
c(t ) = 1 − e
−
t T
t≥0
由于c(t)的终值为1,系统稳态误差为0。 由于c(t)的终值为1,系统稳态误差为0 c(t)的终值为1,系统稳态误差为 动态性能指标： 动态性能指标：
输入信号 输入信号 时域） 复频域） （时域） （复频域） 输出响应 传递函数
δ (t )
1 ⋅ (t )
1
1 s 1 2 s 1 s3
1 e T
−
t T
t≥0
t T
1− e
ห้องสมุดไป่ตู้
−
t≥0
− t T
t
1 2 t 2
t − T + Te
t≥0
− t T
1 Ts + 1
1 2 t − Tt + T 2 (1 − e 2
R(s)
－
100
C(s)
s
3.2一阶系统

3.2一阶系统


± ts = 3T (±5%) ± ts = 4T (±2%)
es =1− =0 1 s
第二节 一阶系统性能分析
2．单位斜坡响应 ．
单位斜坡响应曲线 1 R(s)= 1 C(s)= Ф(s)• 2 2 s h(t) s 1 • 1 = Ts+1 s2 T 1 - T T = s2 s + s+1/T 0 t 单位斜坡响应为: 单位斜坡响应为
Cs () 3 ( Φs)= = Rs 2 +4 () s
时间常数T 时间常数T
T=?
二、一阶系统时域响应及性能分析
1．单位阶跃响应 ．单位阶跃响应
系统在单位阶跃信号作用下的输出 系统在单位阶跃信号作用下的输出. 单位阶跃信号作用下的输出
r(t ) = 1(t )
1 R (s ) = s
1 1 1 1 C(s ) = R(s ) ⋅ Φ(s ) = ⋅ = − s Ts + 1 s s + 1 / T
第二节 一阶系统性能分析 − c t)=ht)=1−e t/T ( ( 一阶系统单位阶跃响应曲线
c(t)
0.98 1 0.95 0.86 0.632
0
T 2T 3T 4T
t
态 差 稳 误 es =r−c s ss
一阶系统没有超调，动态性能指标调节时间 一阶系统没有超调，动态性能指标调节时间ts为:
c t)=ht)=1−e ( (
t − /T
第二节 一阶系统性能分析
根据系统的输出响应求取系统的性 能指标,从而分析系统的性能 从而分析系统的性能， 能指标 从而分析系统的性能，是时域分 析法分析系统性能的基本方法。 析法分析系统性能的基本方法。
一、一阶系统的数学模型 二、一阶系统的时域响应及性能分析
自动控制原理-第3章

自动控制原理-第3章


响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4＜ζ＜0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
自动控制原理3.2 一阶系统的时域分析

自动控制原理3.2 一阶系统的时域分析


何阶线性系统，但不适用于非线性系统。
t
t
T )T
表明一阶系统在过渡过程结束后，其稳态输出与单
位斜坡输入之间，在位置上仍有误差。
4．对斜坡响应求导：dc(t ) dt
t
1e t
c阶 (t)
即单位斜坡响应的导数是单位阶跃响应。
§3—2 一阶系统的时域分析
四、单位抛物线响应：
C(s) 1 1 T T 2 T 2 s3 (Ts 1) s3 s2 s s 1
，若以
1 等速上升到
T
1，所需时间正好为T。
3.t p和 %均没有。t s 4T或t s 3T
T ts 快速性越好。
4、ess 1 c() 0
二．单位脉冲响应：
C(s) 1 1 1 , Ts 1 T s 1 T
g (t )
1 T
§3—2 一阶系统的时域分析
c(t )

1
t2
Tt

T
2 (1
t
eT
)
T
2
t
e(t) r(t) c(t) Tt T 2 (1 eT）
t
故e ss

lim e(t)
t

lim[Tt
t
T2
T 2eT
]

1．一阶系统不能跟踪抛物线信号。
2．对抛物线响应求导：
dc(t )
t
0.632
可见:c(t ) 单调上
升、非振荡、非
周期。
0
§3—2 一阶系统的时域分析
t
c(t) 1 e T
0.865
t
T
3.2一阶系统的时域分析

3.2一阶系统的时域分析

3.2 一阶系统的时域分析用一阶微分方程描述的系统，称为一阶系统。

实际控制系统中一阶系统不乏其例。

下面分析一阶系统对单位阶跃函数、单位脉冲函数、单位斜坡函数、单位加速度函数的响应。

在分析过程中，设初始条件等于零。

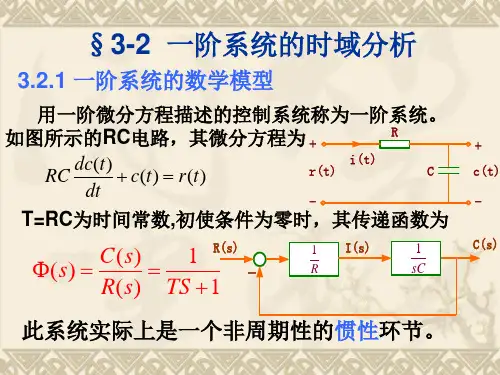
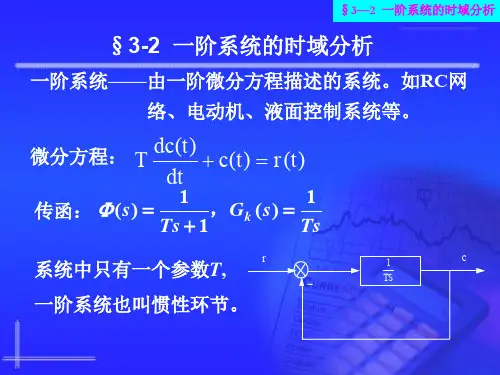
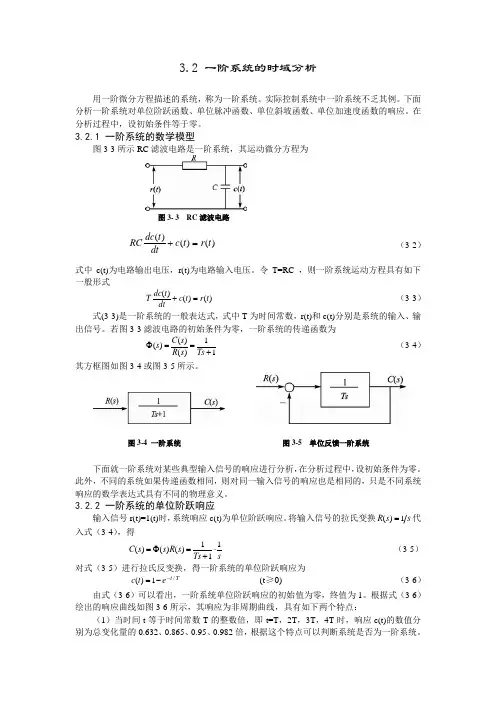
3.2.1 一阶系统的数学模型图3-3所示RC 滤波电路是一阶系统，其运动微分方程为图3- 3 RC 滤波电路)()()(t r t c dt t dc RC =+ （3-2） 式中c(t)为电路输出电压，r(t)为电路输入电压。

令T=RC ，则一阶系统运动方程具有如下一般形式)()()(t r t c dtt dc T =+ （3-3） 式(3-3)是一阶系统的一般表达式，式中T 为时间常数，r(t)和c(t)分别是系统的输入、输出信号。

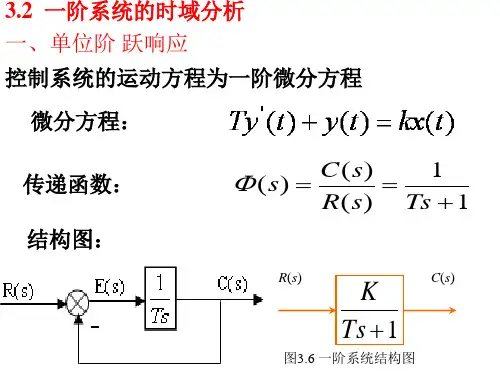
若图3-3滤波电路的初始条件为零，一阶系统的传递函数为11)()()(+==ΦTs s R s C s （3-4）其方框图如图3-4或图3-5所示。

图3-4 一阶系统 图3-5 单位反馈一阶系统下面就一阶系统对某些典型输入信号的响应进行分析，在分析过程中，设初始条件为零。

此外，不同的系统如果传递函数相同，则对同一输入信号的响应也是相同的，只是不同系统响应的数学表达式具有不同的物理意义。

3.2.2 一阶系统的单位阶跃响应输入信号r(t)=1(t)时，系统响应c(t)为单位阶跃响应。

将输入信号的拉氏变换s s R 1)(=代入式（3-4），得sTs s R s s C 111)()()(⋅+=Φ= （3-5） 对式（3-5）进行拉氏反变换，得一阶系统的单位阶跃响应为T t e t c /1)(--= (t ≥0) （3-6） 由式（3-6）可以看出，一阶系统单位阶跃响应的初始值为零，终值为1。

根据式（3-6）绘出的响应曲线如图3-6所示，其响应为非周期曲线，具有如下两个特点：（1）当时间t 等于时间常数T 的整数倍，即t=T ，2T ，3T ，4T 时，响应c(t)的数值分别为总变化量的0.632、0.865、0.95、0.982倍，根据这个特点可以判断系统是否为一阶系统。

3.1典型输入信号 3.2 一阶系统的时间响应

3.1典型输入信号 3.2 一阶系统的时间响应


第三章
控制系统的时域分析
3.2.5线性定常系统时间响应的性质 系统时域响应通常由稳态分量和瞬态分量共同组 成，前者反映系统的稳态特性，后者反映系统的动 态特性。 输入信号决定响应的稳态分量，传递函数决定响应 的瞬态分量∆∆∆。 注意到： 一阶系统的典型输入响应特性与时间常数T密切相 关，时间常数T越小，单位阶跃响应的调节时间越 小，单位斜坡响应的稳态值滞后时间也越小,单位 脉冲响应的衰减越快。
RC电路、恒温箱、液位调节系统、室温调节系统是常见的一阶系统
dxo (t ) T xo (t ) xi (t ) dt
X o ( s) 1 G( s) X i ( s) Ts 1
第三章
控制系统的时域分析
3.2.2 一阶系统的单位阶跃响应 对于单位阶跃输入
xi (t ) 1(t )
t T
单位斜坡响应为：
误差为：
x o (t ) (t T Te
1 t T
) 1(t )
e(t ) xi (t ) xo (t ) T (1 e )
一阶系统跟踪单位斜 坡信号的稳态误差为：
ess lim e(t ) T
t
第三章
控制系统的时域分析
一阶系统单位斜坡响应的特点
第三章
控制系统的时域分析
一阶系统的单位阶跃响应曲线
第三章
控制系统的时域分析
一阶系统单位阶跃响应的特点 响应分为两部分 t T e 瞬态响应： 表示系统输出量从初态到终态的变化过程 （动态/过渡过程）
稳态响应：1
表示t时，系统的输出状态 xo(0) = 0，随时间的推移， xo(t) 指数增大， 且无振荡。 xo() = 1，无稳态误差；

自动控制原理第三章

单击此处添加标题
3.3.1 典型二阶系统的暂态特性
单击此处添加标题
系统的闭环特征方程：
单击此处添加标题
二阶系统的闭环传递函数为
单击此处添加标题
当 时，
特征根：
1. 当 时，特征方程有一对不等的实根，称为过阻尼系 统，系统的阶跃响应为非振荡过程。
3.3.1.1 过阻尼（ ）的情况
特点：由 明显看出，暂态响应曲线应由稳态分量和暂态分量 组成。暂态分量又包含两项衰减的指数项，衰减的快慢取决于指数的 大小。指 数大者衰减快，对最终输出影响小，若将其忽略，二阶 系统的暂态响应就近似为一阶系统。故此时电路的输出量为单调上 升曲线。
分析结论：
由上图可看出： 使得 比 响应迅速且有较大超调量。
PART ONE
闭环传递函数的标准形式如下：
2.二阶系统加极点的暂态响应
其中 是负实数极点 与共轭复数极点的负实部之比。
4） 脉冲函数
在 处的单位脉冲函数用 来表示，它满足如下条件：
单位脉冲函数可看作单位阶跃函数的倒数，即
反之，单位脉冲函数 的积分就是单位阶跃函数。
单位脉冲函数：
面积 A = 1 时脉冲函数，称为单位脉冲函数 。 其拉氏变换后的像函数为 于是，强度为A的脉冲函数 可表示为
单击此处添加大标题内容
结论（1）三阶系统的暂态响应由三部分组成，即 稳态分量 由极点 构成的指数函数项 由共轭复数极点构成的二阶系统暂态响应分量 （2）当 时，系统的暂态特性主要由 和 决 定，系统呈现二阶系统的特性。 当 时，系统的暂态特性主要由 决定， 系统呈现一阶系统特性。 （3）一般情况下， ，因此具有负实数极点的 三阶系统，其暂态特性的振荡性减弱，而 和 增长， 减小，相当于系统的惯性增加了。

一阶系统时域分析

CHAPTER 3 Time Domain Analysis of Control System and Its Characteristics
引言
3.1 动态和稳态性能指标
3.2 一阶系统的时域分析
3.3 二阶系统的时域分析
3.4 线性系统的稳定性分析
3.5 控制系统的稳态误差
3/13/2024
Chapter 2-1
c(t )
r (t )
T c(t)
T
0
T
t
3/13/2024
Chapter 2-1
• 讨论：
• 稳态分量(t-T) 是一个与输入信号等斜率的斜坡 函数，但时间上滞后一个时间常数T。
• 暂态分量 Te，t /T 当 t 时，它按指数规律衰减到 零，衰减速度由极点s=-1/T决定。
• 单位斜坡响应也可由单位阶跃响应积分得到 （其中初始条件为零）。
或ts 3T
ts 4T
3/13/2024
Chapter 2-1
一阶系统的单位加速度响应 对于单位加速度输入
于是
r(t ) 1 t 2 2
R(s)
1 s3
C(s)
1 Ts 1
1 s3
由拉氏反变换可得到一阶系统的单位加速度响应
c(t) 1 t 2 Tt T 2 (1 et/T ) 2
3/13/2024
3/13/2024
Chapter 2-1
• 一阶系统的单位斜坡响应
对于单位斜坡输入
r(t) t 于是
R(s) 1 s2
1 1 1 T T2
C(s) Ts 1 s2
s2
s
Ts 1
由拉氏反变换可以得到一阶系统的单位斜坡响应为

自动控制原理课后答案第3章

第3章 控制系统的时域分析【基本要求】1. 掌握时域响应的基本概念，正确理解系统时域响应的五种主要性能指标；2. 掌握一阶系统的数学模型和典型时域响应的特点，并能熟练计算其性能指标和结构参数；3. 掌握二阶系统的数学模型和典型时域响应的特点，并能熟练计算其欠阻尼情况下的性能指标和结构参数；4. 掌握稳定性的定义以及线性定常系统稳定的充要条件，熟练应用劳斯判据判定系统稳定性；5. 正确理解稳态误差的定义，并掌握系统稳态误差、扰动稳态误差的计算方法。

微分方程和传递函数是控制系统的常用数学模型，在确定了控制系统的数学模型后，就可以对已知的控制系统进行性能分析，从而得出改进系统性能的方法。

对于线性定常系统，常用的分析方法有时域分析法、根轨迹分析法和频域分析法。

本章研究时域分析方法，包括简单系统的动态性能和稳态性能分析、稳定性分析、稳态误差分析以及高阶系统运动特性的近似分析等。

根轨迹分析法和频域分析法将分别在本书的第四章和第五章进行学习。

这里先引入时域分析法的基本概念。

所谓控制系统时域分析方法，就是给控制系统施加一个特定的输入信号，通过分析控制系统的输出响应对系统的性能进行分析。

由于系统的输出变量一般是时间t 的函数，故称这种响应为时域响应，这种分析方法被称为时域分析法。

当然，不同的方法有不同的特点和适用范围，但比较而言，时域分析法是一种直接在时间域中对系统进行分析的方法，具有直观、准确的优点，并且可以提供系统时间响应的全部信息。

3.1 系统的时域响应及其性能指标为了对控制系统的性能进行评价，需要首先研究系统在典型输入信号作用下的时域响应过程及其性能指标。

下面先介绍常用的典型输入信号。

3.1.1 典型输入信号由于系统的动态响应既取决于系统本身的结构和参数，又与其输入信号的形式和大小有关，而控制系统的实际输入信号往往是未知的。

为了便于对系统进行分析和设计，同时也为了便于对各种控制系统的性能进行评价和比较，需要假定一些基本的输入函数形式，称之为典型输入信号。

自动控制原理 第三章 时域分析c1



2时 5时
h(t)
其他动态性能指标：
td 0.69T
tr 2.20T
ts 3T (5%误差带）
16 t
3-2 一阶系统的时域分析
自控原理
3.一阶系统单位脉冲响应
当输入信号为理想单位脉冲函数δ (t)时，R(S)＝1，输出量的拉氏
变换与传递函数相同，即 C(s) 1 TS 1
t
eT
)
t0
2
S3
2
上述几种典型响应有如下关系：
积分
积分
积分
单位脉冲
单位阶跃
单位斜坡
函数响应
函数响应
函数响应
微分
微分
微分
单位抛物线 函数响应
20
3-2 一阶系统的时域分析
自控原理
例: 设某高阶系统可用下列一阶微分方程近似描述：


T ct ct rt rt
其中， 1 (T ) 0
结论：一阶系统无法跟踪加速度形式的输入信号
19
3-2 一阶系统的时域分析
自控原理
输入信号 输入信号
时域
频域
输出响应
传递函数
(t)
1
1
t
eT
T
(t 0)
1
1(t)
S
t
1e T t 0
1
t
1
t
TS 1
S2
t T Te T t 0
1 t2
1
1
t2
Tt

T
2 (1
2.能熟练运用劳斯稳定性判据判断系统的稳定性
3.正确理解对控制信号和干扰作用的稳态误差定义， 能熟练应用静态误差系数法计算稳态误差。

自动控制原理 第3章时域分析

该曲线的特点是：在t＝0处曲线的斜率最大，其值为 1/T。若系统保持初始响应的变化率不变，则当t＝T时输出 就能达到稳态值，而实际上只上升到稳态值的63.2%，经过 4T的时间，响应达到稳态值的98％。显然，时间常数T反映 了系统的响应速度。
16
1)暂态性能指标 tr＝2.2T (按第二种定义) ts＝4T (Δ＝±2%) 2)稳态性能指标
ess
lim[r(t)
t
c(t)]
0
17
3.2.3 单位脉冲响应
对于单位脉冲输入r(t)＝δ(t)，R(s)＝1，于是
C(s)
1 Ts 1
1 T
s
1 1
T
因此
(3-7)
g(t)
c(t)
1
t
eT
(t 0)
(3-8)
T
18
响应曲线如图3-5所示。该曲线在t＝0时等于1/T，正好 与单位阶跃响应在t＝0时的变化率相等，这表明单位脉冲响 应是单位阶跃响应的导数，而单位阶跃响应是单位脉冲响
3
3.1 控制系统的时域性能指标
评价一个系统的优劣，总是用一定的性能指标来衡量。
系统的时域性能指标是根据系统的时间响应来定义的。
控制系统的时间响应通常分为两部分：稳态响应和暂
态响应。如果以c(t)表示时间响应，那么其一般形式可写为
c(t)＝css(t)＋ct(t)
式中：css(t)为稳态响应；ct(t)为暂态响应。
(3-1)
4
稳态响应由稳态性能描述，而暂态响应由暂态性能描 述。因此，系统的性能指标由稳态性能指标和暂态性能指 标两部分组成。
5
3.1.1 暂态性能指标
控制系统常用的输入信号有脉冲函数、阶跃函数、斜 坡函数、抛物线函数以及正弦函数等。通常，系统的暂态 性能指标是根据阶跃响应曲线来定义的，如图3-1所示。

自动控制原理(第二版)(赵四化)章 (3)


(s) C(s) 1
R(s) Ts 1
(3-13)
第3章 时域分析法 图3-5 一阶系统的动态结构图
第3章 时域分析法
3.2.1 一阶系统的单位阶跃响应
设输入
R(s) 1 s
则输出量的拉氏变换为
C(s) (s) 1 1 1 1 1
s Ts 1 s s s 1/T
单位阶跃响应为
1t
C(s)
(s)R(s)
s2
n2 2ns
n2
1 s
其中, 由
s2 2 ns n2 0
可求得两个特征根
s1,2 n n 2 1
(3-22)
第3章 时域分析法
1) ξ>1, 过阻尼
ξ>1
时
, 2 1 s1,2=-ξωn±ωn
为两个不相等的负实数根， 即有
C(s)
n2
A1 A2 A3
(s)
C(s) R(s)
s2
n2 2ns
n2
(3-21)
其中， ξ为阻尼比， ωn为无阻尼自然振荡频率， 它们 均为系统参数。
第3章 时域分析法
由式(3-21)可以看出， 二阶系统的动态特性 可以用ξ和ωn这两个参数的形式加以描述。 如果0<ξ<1， 则闭环极点为共轭复数， 并且位于左半s平面， 这时系统 叫做欠阻尼系统， 其瞬态响应是振荡的。 如果ξ=1， 那 么就叫做临界阻尼系统。 而当ξ>1时， 就叫做过阻尼系 统。 临界阻尼系统和过阻尼系统的瞬态响应都不振荡。 如果ξ=0， 那么瞬态响应变为等幅振荡。
此时系统输出响应的拉氏变换为
C(s)
1 Ts 1
1 s2
1 s2
T s
T2 Ts 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
11 C(s)
Ts 1 s3
1 T T2 T2 s3 s2 s s 1
T
c(t
)
1
t
2
Tt
T
2
(1
t
eT
)(t
0)
2
e(t
)
r
(t
)
c(t
)
Tt
T
2
(1
e
t T
)
跟踪误差随时间推移而增大，直至无限大。因此，一阶系统 不能实现对加速度输入函数的跟踪。
R(s)＝1
c(s) 1 (s) Ts 1
可知，输出量的拉氏变换与系统的传递函数相同， 这时输出称为单位冲激响应，记作h(t)
h(t) c(t) Lt
0)
T
3 一阶系统的单位速度响应
Unit-ramp Response of first-order Systems
r(t) t 11
表1:一阶系统对典型输入信号的响应
输入信号
(t)
1(t)
t
1 2
t
2
输出响应
1
t
eT
,t
0
T
t
1e T ,t 0
t
t T Te T , t 0
1 2
t2
Tt
T
2
T
2eTt
,
t
0
•系统对输入信号导数的响应，等于系统对该输入信号响应的导数 •系统对输入信号积分的响应，等于系统对该输入信号响应的积分； 积分常数由零初始条件确定。
C(s) Ts 1 s2
t
c(t) t T Te T (t 0) cs ct
Cs=t-T是稳态分量，也就是速度函数与输入信号斜率相同，时间 滞后一个时间常数T。
Ct按指数规律衰减到零，衰减速度由极点决定
ess
lim
t
e(t)
lim[r(t)
t
c(t)]
T
4 一阶系统的单位加速度响应
r(t) 1 t2 2
r(t) 1 R(s) 1/ s
C(s) (s)R(s) 1 1 1 T Ts 1 s s Ts 1
t
c(t)
1 e
T
(t
0)
cs (t)
ct
(t
)1
T
稳态分量 暂态分量
R(s)的极点形成系统响应 的稳态分量。
传递函数的极点是产生系 统响应的瞬态分量。
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
响应速度与时间常数T成反 比，T越小，响应速度越快。
延迟时间： 上升时间： 调节时间： 超调量： 稳态误差：
td=0.69T tr=2.2T ts=3T (=5%) ess=0
4T (= 2%)
2 一阶系统的单位冲激响应
Unit-impulse response of first-order systems
一阶系统的时域分析
R(s)
1
C(s)
Ts
(s) C(s) 1 R(s) Ts 1
将典型输入信号加入系统 通过分析系统时域响应来得到系统的性能指标（动态、稳态）
1 单位阶跃响应
(s) C(s) 1 R(s) Ts 1
Unit-Step Response of First-order System
第三章 线性系统时域分析法
3.2 一阶系统的时域分析
3.2 一阶系统的时域分析
输入信号r(t)与输出信号c(t)的关系
T dc(t) c(t) r(t) dt
用一阶微分方程表示的系统称为一阶系统
(s) C(s) 1 R(s) Ts 1
常见的温度控制系统和液压控制系统中的被控对象都是一阶系统