当前位置：文档之家 › 高三数学函数的连续性与导数的概念PPT优秀课件

高三数学函数的连续性与导数的概念PPT优秀课件

  • 格式：ppt
  • 大小：348.00 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

《函数的连续》课件

《函数的连续》课件
在闭区间上的连续函数一定取得最大值和最小值。
闭区间上连续函数的零点定理
如果闭区间上的连续函数在区间两端取值异号，则函数在该区间内至少有一个零点。
03
函数连续性的应用
利用连续性求极限
总结词
利用连续性求极限是函数连续性应用的重要方面之一。
详细描述
在数学分析中，许多函数的极限可以通过利用函数的连续性来求解。例如，利用函数在某点的连续性 ，可以推导出该点的极限值。此外，连续函数的极限定理也是利用连续性求极限的重要工具。
二次函数
二次函数在定义域内也是连续的 。例如，函数$f(x) = x^2$在全 体实数域$mathbf{R}$上是连续 的。
分段函数的连续性
• 分段函数：分段函数在各段定义域的交界处可能不连 续，但在整个定义域内是连续的。例如，函数$f(x) = \begin{cases} x^2, & x \geq 0 \ x, & x < 0 \end{cases}$在全体实数域$\mathbf{R}$上是连续的 ，但在$x=0$处不连续。
函数连续性的性质
Байду номын сангаас
如果内层函数和外层函数都在 某点连续，则复合函数在该点
也连续。
02
反函数的连续性
01
复合函数的连续性
反函数存在的前提下，如果原函 数在某点连续，则反函数在该点
也连续。
02
函数连续性的判定
函数在某点连续的判定
函数在某点连续的定义
如果函数在某一点的极限值等于该点的函数值，则函数在该点连续。
无穷函数的连续性
• 无穷函数：无穷函数在无穷处的值可能不定义，因此不连续。 例如，函数$f(x) = \frac{1}{x}$在$x=0$处不连续。

高三数学函数的连续性与导数的概念_课件a

高三数学函数的连续性与导数的概念_课件a
函数在区间上连续
如果函数在区间内的每一点都连续， 则函数在该区间上连续。
Байду номын сангаас
函数连续性的性质
01
连续函数的和、差、积、商（分母不为零）仍为连 续函数。
02
连续函数的复合函数仍为连续函数。
03
连续函数的反函数仍为连续函数（反函数的定义域 和值域需满足条件）。
函数连续性的判定
判断函数在某一点是否连续，可以通 过计算该点的极限值并与该点的函数 值进行比较。
导数还可以用来确定函数的极值点，当一阶导数在该点由正变负或由负变正时，该点即为函数的极值 点。
详细描述
在极值点处，函数的导数等于0或不存在。通过求函数的二阶导数并分析其正负，可以判断该极值点 是极大值还是极小值。
导数与函数的拐点
总结词
导数还可以用来寻找函数的拐点，即函数图像的凹凸分界点。通过求函数的二阶导数并分析其正负，可以确定拐 点的位置。
在弹性力学中，连续性和导数用于描述物体的弹性和应力分布。
热传导
在热传导问题中，连续性和导数用于描述温度随时间和空间的变化 。
经济问题中的应用
供需关系
通过连续性和导数分析商品的价格与需求量、供应量之间的关系 。
投资回报
连续性和导数用于计算投资回报率，评估投资风险和收益。
经济增长
连续性和导数用于分析经济增长的速率和趋势。
求函数$f(x) = sin(x) + cos(x)$的最小正周 期。
综合习题
综合习题1
求函数$f(x) = x^2 + sin(x)$在区间$[0, 2pi]$上 的零点个数。
综合习题2
证明函数$f(x) = e^x - x - 1$在$R$上只有一个 零点。

第六节函数的连续性PPT课件

第六节函数的连续性PPT课件

1
x1
o1
x
x 1为函数的可去间断点.
【说明】 可去间断点只要改变（原来有定义时）或 者补充（原来无定义时）间断点处函数的定义, 则 可使其变为连续点，故称其为可去间断点.
17
第17页/共55页
如例5中, 令 f (1) 2,
y
则
f
(x)
2 1
x, x,
0 x 1, x 1,
2 1
在x 1处连续 .
22 故 y arcsin x 在[1,1]上也是单调增加且连续 同理 y arccos x 在[1,1]上单调减少且连续
y arctanx, y arccot x 在(,)上单调且连续
【结论】反三角函数在其定义域内皆连续.
26
第26页/共55页
2、复合函数的连续性
【定理3】若 lim x x0
1, 1,
当x是有理数时, 当x是无理数时,
课后习题P65 5（2）反例
在定义域R内每一点处都间断, 但其绝对值处 处连续.
【观察练习】立即说出下列间断点类型:
y
y f x
x1 o
x2
x3
第22页/共55页
x
22
又如:
x
2
x0
x1
y
y tan x
o
x 无穷间断点
2
y y sin 1 x
振荡间断点
x
【解】在x 0处没有定义,
且 limsin 1 不存在. x0 x
y sin 1 x
x 0为第二类间断点.
这种情况称为振荡间断点.
【特点】 f ( x0 ) 与 f ( x0 )中至少有一个因函数 振荡而不存在，但均不为∞，称之.

高等数学-函数的连续性课件.ppt

高等数学-函数的连续性课件.ppt
(1)在x=1处有定义；
(2)函数在x=1处的左右极限相等，即函数在x=1处的极限存在，且等于2，但不等于f (1)
导致函数图象断开的原因：
1、函数在 处没有定义
2、函数在 时极限不存在
函数值不等
3、函数在 处的极限值和
o
x
y
1
2
1
2
o
x
y
2.5
y
x
o
1
2
在
在
二、 函数的间断点
但是由于
x
y
O
1
右极限存在，
因为，如果修改定义 f (0) = 1，
在 x = 0 连续.
则函数
x
y
O
1
内容小结
左连续
右连续
第一类间断点
可去间断点:
跳跃间断点: 左右极限不相等
第二类间断点
无穷间断点:
振荡间断点: 函数值在 的去心邻域
(左右极限至少有一个不存在)
在点
间断的类型
在点
连续的等价形式
一、 函数连续性的定义
1.变量的增量
设变量 从它的一个初值 变到终值 终值与初
值的差 就叫做变量u的增量 记作
即
注：
不表示某个变量 与u的乘积，而是一个
整体不可分割的记号.
设函数y = f (x)在点 的某一个邻域内是有定义的
当自变量 在这邻域内从 变到 时函数y相应
思考题
间断点的类型.
解: 间断点
为无穷间断点;
故
为跳跃间断点.
1. P49 题 5
2. 确定函数
分析 所给函数是极限的形式，首先应求出不同区间的极限，给出函数的分段函数表达式，然后再研究间断点及其类型。

(新版)高数PPT课件：连续,导数、微分

(新版)高数PPT课件：连续,导数、微分

dy dx
或
x x0
df ( x) dx
, x x0
即
y
x x0
y lim x x0
lim
x0
f
( x0
x) x
f ( x0 )
其他形式
f
( x0 )
lim
h0
f
( x0
h) h
f
(x0 ) .
f
(
x0
)
lim
x x0
f (x) f (x0 ) . x x0
關於導數的說明：
★ 点导数是因变量在点x0处的变化率,它 反映了因变量随自变量的变化而变化的快 慢程度.
幾何解釋:
y
连续曲线弧 y f ( x)的两个 端点位于x轴的不同侧,则曲 a o
y f (x) 1 2 3 b x
线弧与 x轴至少有一个交点.
定理 4(介值定理) 设函数 f (x)在闭区间 a,b
上连续，且在这区间的端点取不同的函数值
f (a) A 及 f (b) B ,
那末，对于A 与B 之间的任意一个数C ，在开区间
又 f (0) 1 0, f (1) 2 0, 由零點定理,
(a, b), 使 f ( ) 0, 即 3 4 2 1 0,
方程x3 4x2 1 0在(0,1)内至少有一根 .
例2 设函数 f ( x)在区间[a, b]上连续, 且f (a) a,
f (b) b. 证明 (a, b), 使得 f ( ) .
1.跳躍間斷點 如果 f ( x)在点 x0处左, 右极限都
存在,但f ( x0 0) f ( x0 0), 则称点 x0为函数 f ( x)的跳跃间断点.
例4

数学分析之函数的连续性PPT课件

数学分析之函数的连续性PPT课件

( 2 )
注 意 到 ( 2 ) 式 在 x x 0 时 恒 成 立 , 因 此 0 x x 0
可改写为 xx0 ， 这样就得到函数 f (x) 在点x0
连 续 的 e 定 义 .
定义2 设 f ( x ) 在 点 x 0 的 某 个 邻 域 内 有 定 义 . 如果
对任意的e 0, 存在 0,当 xx0 ,时
f(x )f(x 0)e,
则 称 f( x )在 点 x 0 连 续 .
为 了 更 好 地 刻 划 函 数 在 点 x 0 的 连 续 性 , 下 面 引 出 连续性的另外一种表达形式. 设 x x x 0 ,
y y y 0 f ( x ) f ( x 0 ) f ( x 0 x ) f ( x 0 )
e 而不是用术语“ 对 于 任 意 的 0 ” ,这 样 可 求 得
| f (x) | 的一个明确的上界.
定理4.3（局部保号性）若 函 数 f 在 点 x 0 连 续 , 且 f ( x 0 ) 0 ( 或 f ( x 0 ) 0 ) ,则对任意一个满足
0 r f ( x 0 ) 或 ( f ( x 0 ) r 0 ) 的 正 数 r , 存 在 0 , 当 x ( x 0 , x 0 ) 时 ,
定义3 设 函 数 f ( x ) 在 点 x 0 的 某 个 右 邻 域 U ( x 0 ) (左邻 U(域 x0))有定义，若
x l x 0 if ( m x ) f ( x 0 )( x l x 0 if ( m x ) f ( x 0 )), 则 称 f ( x ) 在 点 x 0 右 ( 左 ) 连 续 . 很明显, 由左、右极限与极限的关系以及连续函数 的定义可得：
2
2
coxs( x)1, 2

《高等数学导数》课件

《高等数学导数》课件

答案
2. 求下列函数的极值：
$f'(x) = 3x^2 - 6x + 2$，极值点为 $x=1 pm sqrt{2}$，极大值为 $f(1+sqrt{2}) = 1 + 2sqrt{2}$，极小值为 $f(1-sqrt{2}) = 1 - 2sqrt{2}$。
$f'(x) = ln x + 1$，极值点为 $x=1$，极大值为 $f(1) = 0$。
《高等数学导数》ppt 课件
contents
目录
• 导数的基本概念 • 导数的计算 • 导数的应用 • 导数的扩展 • 习题与答案
CHAPTER 01
导数的基本概念
导数的定义
总结词
导数是函数在某一点的变化率，表示 函数在该点的切线斜率。
详细描述
导数定义为函数在某一点附近取得的 最小变化率，即函数在这一点处的切 线斜率。导数的计算公式为lim(x→0) [f(x+h) - f(x)] / h，其中h趋于0。
2. 求下列函数的极值：
01
03 02
习题
$f(x) = frac{1}{x}$
$f(x) = e^x$
答案
01
1. 求下列函数的导数：
02
$y' = 2x + 2$
03
$y' = -frac{1}{x^2}$
答案
• $y' = \sin x + x \cdot \cos x$
答案
• $y' = e^x$
总结词
导数的四则运算在解决实际问题中具 有广泛的应用，例如在经济学、物理
学和工程学等领域。
详细描述
导数的四则运算法则是基于极限理论 推导出来的，通过这些法则，可以方 便地求出复杂函数的导数。

高等数学导数的概念ppt课件.ppt

高等数学导数的概念ppt课件.ppt

x0 处的右 (左) 导数, 记作
y
y x
o
x
机动 目录 上页 下页 返回 结束
定理2. 函数 是
在点 可导的充分必要条件 且
简写为 f (x0) 存在
f(x0 )
定理3. 函数 在点 处右 (左) 导数存在
在点 必 右 (左) 连续.
若函数
在开区间
内可导, 且
都存在 , 则称
在闭区间
上可导.
显然:
f
(0)
lim
x 0
sin x
x
0
0
1
ax 0
f
(0)
lim
x 0
x0
a
故 a 1 时
此时
在
都存在,
机动 目录 上页 下页 返回 结束
作业
P49 5 , 7, 9
第二节 目录 上页 下页 返回 结束
备用题
1. 设
存在, 且
求
解: 因为
1 f (1 (x)) f (1)
lim
2 x0
(x)
在闭区间 [a , b] 上可导
与 f(b)
机动 目录 上页 下页 返回 结束
练习：讨论下列函数在x=0时候的连 续性与可导性.
练习：习题2.1题8
f
x
xk
sin
1 x
,
x0
0, x 0.
若函数在x 0连续，则
lim f x lim xk sin 1 f 0 0,
x0
x0
x
必须满足 lim xk 0， k 0即可. x0
反例:
在 x = 0 处连续 , 但不可导. o
x
机动 目录 上页 下页 返回 结束

函数的连续性(课件)

函数的连续性(课件)
四、函数的连续性
(一)、连续的定义 1.函数的增量
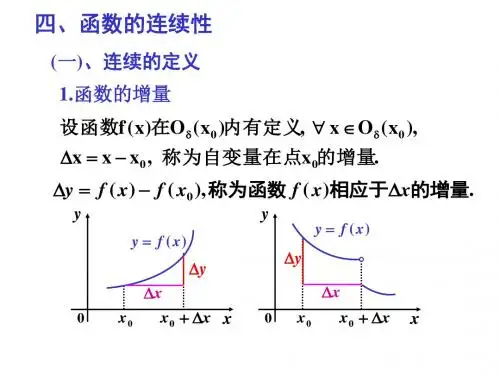
设函数f ( x)在O ( x0 )内有定义, x O ( x0 ), x x x0 , 称为自变量在点x0的增量.
y f ( x ) f ( x0 ), 称为函数 f ( x )相应于x的增量.
y
y f ( x)
x0
要使 f (0 0) f (0 0) f (0), a 1, 故当且仅当a 1时, 函数 f ( x )在 x 0处连续.
(三)、连续函数的性质
若函数f ( x ), g( x )在点x0处连续, 则 f ( x ) g( x ), f ( x) f ( x ) g( x ), (g( x0 ) 0)在点x0处也连续. g( x )
2)可去间断点 lim f ( x) A , 但(1)A f ( x0 ),
x x 0
或( 2) f ( x)在点x0处无定义 则称点x0为函数f ( x)的可去间断点.
注意 可去间断点只要改变或者补充间断处函 数的定义, 则可使其变为连续点.
例5
讨论函数 2 x , 0 x 1, f ( x ) 1, x1 x 1, 1 x, 在x 1的连续性
y
y
x
y f ( x)
y
x
0
0
x0
x 0 x x
x0
x 0 x
x
2.连续的定义
定义2.9 设函数y f(x)的定义域为D, x0 D, 若 lim f ( x) f ( x0 ), 则称f ( x)在x0连续.
x x 0
x0称为f ( x)的连续点.
与 lim f ( x) A定义的区别在于:

函数的连续性(课件

函数的连续性(课件
数学上，如果函数$f(x)$在点$x_0$处的极限值为$f(x_0)$，即 $lim_{x to x_0} f(x) = f(x_0)$，则称$f(x)$在点$x_0$处连续。
函数在区间上的连续性
函数在区间上的连续性是指，对于该区间内的任意一点，函数在该点都连续。如 果一个函数在某个闭区间$[a, b]$内的每一点都连续，则称该函数在区间$[a, b]$ 上连续。
THANKS FOR WATCHING
感谢您的观看
闭区间上的连续函数满足中值定理， 即如果一个闭区间上的连续函数在两 端取值相等，则该函数在这个区间内 至少有一个不动点。
闭区间上的连续函数具有介值性质， 即如果一个闭区间上的连续函数在两 端取值异号，则该函数在这个区间内 至少有一个零点。
连续函数在无穷区间上的性质
连续函数在无穷区间上可以取到无穷大或无穷小 的值。
一致连续性
总结词
如果一个函数在其定义域内的任意两点x1 和x2，当x1趋近于x2时，函数值也趋近于 相同值，则称该函数一致连续。
VS
详细描述
一致连续性是连续函数的一个重要性质， 它表明函数在定义域内的任意两点之间的 变化都是均匀的。一致连续的函数在定义 域内不会出现剧烈的波动或间断，因此其 性质比较稳定。这个性质在解决一些数学 问题时也非常有用，例如求解函数的极限 等。
连续函数与不等式的关系
连续函数在定义域内的单调性可以用来证明不等 式。
3
利用连续函数证明不等式的方法
通过构造函数、利用函数的单调性、求导数等手 段，将不等式问题转化为连续函数的性质问题。
利用连续函数解决实际问题
实际问题的数学模型
实际问题通常需要建立数学模型进行描述和求解。
连续函数与实际问题的关系
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第84讲 函数的连续性与导数的 概念
复习目标及教学建议 基础训练 知识要点
规律总结
复习目标及教学建议
复习目标
掌握函数在某点处连续，在开区间、闭区间上 连续的定义与判定方法，知道函数在某点处不连续 三种类型.了解导数的实际背景，理解导数的定义， 掌握导数的几何意义.
教学建议
本讲的重点是导数的定义及利用导数求曲线的 切线方程.
∴f(x)在x=1处不连续. 即x=1是此函数的不连续点.
第84讲 函数的连续性与导数的概念
2008高考复习方案
例2 设f(x)= x-1(0<x≤1), 2-x(1<x≤3).
（1）求f(x)在点x=1处的左、右极限.在点x=1 f(x)
（2）f(x)在点x=1
（3）求函数f(x)的连续区间；
（4
数f(x)在闭区间［a,b］上连续，除要求在其相应的开区间
内(a,b)连续外，对端点只要求在左端点a处右连续，在右
端点b处左连续.
第84讲 函数的连续性与导数的概念
2008高考复习方案
3 如果函数f(x)在闭区间［a,b］上是连续函数，那么f(x)在 闭区间［a,b］上有最大值和最小值.
4 曲线y=f(x)上两点P、Q，Q在P附近，则PQ称为曲线的割 线，当Q沿曲线无限接近点P，若割线PQ有极限位置，则 割线PQ的极限位置叫做曲线上点P的切线.
第84讲
2008高考复习方案
双基固化
1．函数的连续性
函数的连续性与导数的概念
例1
（1）f(x)= （2）f(x)=
x2 1 x2 3x 2
x
tan x
（3）f(x)= x-1(x≤1)
3-x(x>1).
第84讲 函数的连续性与导数的概D念
2008高考复习方案
【解析】（1）由x2-3x+2=0得x=1或x=2，
第84讲 函数的连续性与导数的概D念
2008高考复习方案
g'(a)limg(x)g(a)limf(x)f(a), x a xa x a xa
第84讲 函数的连续性与导数的概念
2008高考复习y= x2 (x≥1) x-1(x<1)
③y= 2x+1 (x≠0)
0(x=0)
④y=sinx
其中在(-∞，+∞)不连续的函数有（ D ）
2008高考复习方案
A．0
第84讲 函数的连续性与导数的概念
2008高考复习方案
3．下列命题中假命题是
（ C）
A
B
C
D．抛物线的切线与抛物线只有一个交点
第84讲 函数的连续性与导数的概D念
2008高考复习方案
4．若f′(x0)=2，则 limf(x0k)f(x0等) 于 (
k 0
2k
A)
A．-1
B．-2
C．1
D．1
2
【解析】
第84讲 函数的连续性与导数的概D念
5 曲线上有两点（x0，f(x0)），（x0+Δx）， f（x0+Δx））.当Δx→0时， f(x0x)f(极x0)限存在，称y=f(x) 在x0处可导.并把这个极限值称f(xx)在x0处的导数.
第84讲 函数的连续性与导数的概念
2008高考复习方案
6．导数的物理意义 函数s=s(t)的导数s′(t)表示t时刻的瞬时速度，即v=s′(t). 瞬时速度v=v′(t)的导数v′=v′(t)是t时刻的加速度. a=v′(t). 7 若函数f(x)在x0处可导，则f′(x0)是以点（x0，f(x0)） 为切点的切线的斜率. 8 可导一定连续，连续不一定可导.
x 1 x 1 x 1
（2）由于f(x)在点x=1处的极限不存在，故f(x)在x=1
处不连续.
（3）函数的连续区间是(0,1］,(1,3］.
（4）∵点x= 1 ，x=2均在函数的连续区间内，
limf(x)2 limf(x1)111,
x 1
x 1
22
2
2
limf(x)limf(x2)22=0
第84讲 函数的连续性与导数的概念
2008高考复习方案
知识要点
1．函数f(x)在点x0
（1）函数f(x)在点x=x0
（2）函数f(x)在点x=x0处有极限；
（3） l i m f(x)=f(x0).
2
x x0
函数f(x)在开区间(a,b)内连续，只要求在开区间(a,b)
内任何点处连续即可，对在端点a,b处是否连续不要求.函
B．1
C．2
D．3
【解析】①、②、③为函数不连续的三种类型.
2．已知函数f(x)在x=x0处及附近有定义，给出下列三
① l i m f(x)=f(x0)
x x0
lim
x x0
f(x)=
li
x
m
x0
(x)
l i m f(x)=f(x0)
则函x 数x 0 f(x)在x=x0处连续的充要条件是①.
第84讲 函数的连续性与导数的概D念
2008高考复习方案
5．若曲线y=h(x)在x=a处的切线方程为2x+y+1=0，
那么
(A)
A．h′(a)<0
B．h′(a)>0
C．h′(a)=0
D. h′(a)
【解析】由导数几何意义可知，h′(a)是曲线在
点P处切线的斜率，又由切线方程2x+y+1=0可知
其斜率为-2，所以h′(a)=-2<0.故选A．
limf(x),limf(x).
x1
x2
2
【解析】（1）x li m 1 f(x ) l x i m 1f(x 1 ) 0 ,
lim f( x ) ,lim f( 2 x ) 1 ,
x 1
x 1
第84讲 函数的连续性与导数的概念
2008高考复习方案
l i m f ( x ) l i m f ( x ) , l i m f ( x ) 不 存 在
∴函数的不连续点为x=1和x=2.
（2）当x=kπ(k∈Z)时，tanx=0，当
x=kπ+ π (k∈Z时，tanx不存在，故函数f(x)=x
的不连续2 点为x=kπ和x=kπ+ π (k∈Z).
tan x
2
（3）∵f(x)的定义域为(-∞，+∞)
第84讲 函数的连续性与导数的概D念
2008高考复习方案
x 2
x 2
第84讲 函数的连续性与导数的概念
2008高考复习方案
2．导数的概念及几何意义的应用 例3 设f(x)在R上可导. （1）利用定义求：f(-x)在x=a处的导数与f(x)在x=-a处 的导数之间的关系. （2）利用定义证明：若f(x)为偶函数，则f′(x)为奇函数.
【证明】（1）记f(-x)=g(x)，则f(-x)在a处的导数为 g′(a)，于是