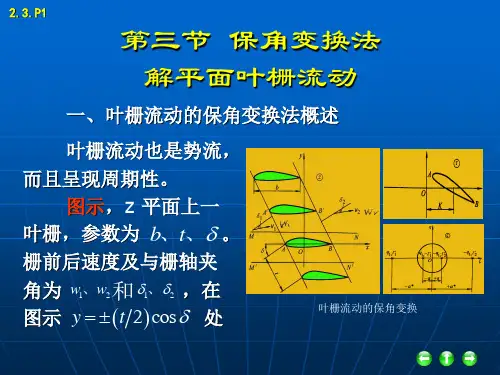
保角变换法
- 格式:ppt
- 大小:676.00 KB
- 文档页数:18


基于保角变换法富水软土高速公路隧道渗流场分析摘要:针对高水压工况下地下水渗流引起的高速公路隧道开挖失稳破坏问题,以贵金高速公路隧道工程为背景,基于隧道围岩渗流场理论,运用有限元软件建立隧道开挖渗流场模型,总结出不同影响因素对衬砌外水压力、孔隙水压力和岩体强度特性的变化规律,提出了维持富水隧道开挖面稳定性的关键施工技术。
研究结果表明:隧道衬砌外水压力随着θ角近似呈正弦函数曲线分布特征,当隧道埋深d=2R时,衬砌内外处于等水压状态;孔隙水压力与地下水位和渗流时间近似呈正相关关系,当开挖面支护压力比小于0.5时,隧道围岩处于失稳临界状态;注浆加固后拱顶沉降降幅为37.07%。
研究结果可为类似工程提供借鉴和参考。
关键词:富水软土隧道;保角变换法;渗流场;孔隙水压;岩体强度特性;控制参数中图分类号:U 455文献标志码:AAnalysis of seepage field of water-rich soft soil highway tunnel based on conformal transformation methodLUO Hong-guang, CHEN Ze-meng(CCCC—SHEC Forth Engineering Co.Ltd., Luoyang, Henan, 471013, China)Abstract:Aiming at the problem of unstable failure of highway tunnel excavation caused by groundwater seepage under high water pressure conditions, Based on the theory of tunnel surrounding rock seepage field in Guijin Expressway tunnel project, The finite elementsoftware is used to establish the seepage field model of tunnel excavation. The changes of different influencing factors on theexternal water pressure, pore water pressure and rock mass strength characteristics of the lining were summarized, and the keyconstruction technologies to maintain the stability of the excavation surface of water-rich tunnels are proposed. The results show that the water pressure outside the tunnel lining showed the distribution characte ristics of sinusoidal function curve with the θ angle approximation, When the tunnel is buried at depth d=2R, the lining inside and outside are in a same water pressure state. Pore water pressure is approximately positively correlated with groundwater level and seepage time. When the support pressure ratio of the excavation surface is less than 0.5, the surrounding rock of the tunnel is in an unstable critical state. After grouting reinforcement, the settlement reduction of the vault was 37.07%. The research results can provide reference for similar projects.Key words:water-rich soft soil tunnel; conformal transformation method; seepage field; pore water pressure; rock mass strength characteristics; control parameters随着我国基础交通建设的大力发展,高速公路在穿越高水压高渗透复合地层等复杂地质条件时,会弱化岩体强度,造成开挖面失稳和坍塌事故。

通俗理解保角变换保角变换是一种数学中常用的线性变换方法,它在图像处理、计算机视觉以及计算机图形学等领域有着广泛的应用。
它可以将一个平面上的任意形状变换为另一个平面上的指定形状,同时保持原始图像的角度不变。
保角变换的原理是基于复平面上的一个定理,即保角变换可以通过将原始图像的每个点映射到一个新的点来实现。
这个新的点的位置是根据原始图像上的每个点的角度和距离来计算的。
换句话说,保角变换是通过对每个点进行角度和距离的调整来实现的。
保角变换的一个重要应用是图像的形变。
通过保角变换,我们可以将一个图像的形状变换为另一个图像的形状,同时保持图像的角度不变。
这在计算机图形学中非常有用,可以用于图像的纠正、图像的拼接以及图像的变形等方面。
另一个重要的应用是图像的纠正。
在拍摄照片或者录制视频时,由于摄像机的位置或角度的问题,导致图像出现畸变。
通过保角变换,我们可以对这些畸变进行纠正,使得图像恢复到原始形状。
除了图像处理领域,保角变换还广泛应用于计算机视觉中。
在计算机视觉中,我们常常需要对图像进行特征提取和匹配。
通过保角变换,我们可以将不同角度和尺度的图像进行统一处理,从而提取出它们的共同特征。
保角变换还可以应用于地图投影。
地球是一个球体,而地图是一个平面,因此在制作地图时必须进行投影。
保角投影是一种常用的地图投影方法,它可以保持地图上各个地区的角度不变,从而更准确地表现出地球的地形。
总的来说,保角变换是一种非常重要的数学变换方法,它在图像处理、计算机视觉以及计算机图形学等领域都有着广泛的应用。
通过保角变换,我们可以对图像进行形变、纠正畸变、提取特征以及制作地图等操作,从而帮助我们更好地理解和处理图像数据。



无限长导体圆柱与无限大导体平面间单位长度的电容——保角变换方法的一例应用一、引言电容是一种重要的电气元件,它的作用是存储电荷和放大电压。
电容的电容量受其外形和材料特性的影响,特别是无限长导体圆柱与无限大导体平面间单位长度的电容量,这是电力系统中的一个非常重要的参数。
本文的目的是通过保角变换法计算无限长导体圆柱与无限大导体平面间单位长度的电容。
二、理论分析无限长导体圆柱与无限大导体平面的电容可以用保角变换法来计算,首先,将无限长导体圆柱和无限大导体平面变换成有限长导体圆柱和有限大导体平面,然后结合复变换计算有限长导体圆柱和有限大导体平面间单位长度的电容,最后再将计算出来的电容变换成无限长导体圆柱与无限大导体平面间的电容,就可以得到所要求的无限长导体圆柱与无限大导体平面间单位长度的电容了。
保角变换法的步骤如下:1)将无限长导体圆柱和无限大导体平面变换成有限长导体圆柱和有限大导体平面,即将无限长导体圆柱和无限大导体平面变换成有限长导体圆柱和有限大导体平面。
2)用复变换计算有限长导体圆柱和有限大导体平面间单位长度的电容,即先给出复变换的方程,然后求解出有限长导体圆柱和有限大导体平面间单位长度的电容。
3)将计算出来的电容变换成无限长导体圆柱与无限大导体平面间的电容,即根据保角变换的公式,变换出有限长导体圆柱和有限大导体平面间单位长度的电容,得到无限长导体圆柱与无限大导体平面间单位长度的电容。
三、特殊情况无限长导体圆柱与无限大导体平面间单位长度的电容,在某些特殊情况下,可以通过简单的计算来获得。
1)当无限长导体圆柱的半径为零时,无限长导体圆柱与无限大导体平面间单位长度的电容等于无限大导体平面间单位长度的电容,即C=2πε/ln22)当无限长导体圆柱的半径趋于无穷大时,无限长导体圆柱与无限大导体平面间单位长度的电容等于无限大导体圆柱与无限大导体平面间单位长度的电容,即C=ε/2四、实验1)准备材料:无限长导体圆柱,无限大导体平面,高频电容计,High-Frequency-Voltmeter,等2)实验步骤:(1)将无限长导体圆柱与无限大导体平面变换成有限长导体圆柱和有限大导体平面;(2)用高频电容计测量有限长导体圆柱和有限大导体平面间单位长度的电容;(3)将测量出来的电容变换成无限长导体圆柱与无限大导体平面间的电容;(4)用High-Frequency-Voltmeter测量无限长导体圆柱与无限大导体平面间单位长度的电容。


茹科夫斯基保角变换
茹科夫斯基保角变换是指一种变换方法,用于把一个凸多边形映射到另一个凸多边形,保持所有角的大小和方向不变。
在数学上,一个茹科夫斯基保角变换可表示为:
z = f(z) = A + B \frac{z-z_0}{\overline{z}-\overline{z_0}}。
其中,z和z_0是原凸多边形和目标凸多边形的顶点坐标,A、B是复数常数,\overline{z}表示z的共轭复数。
茹科夫斯基保角变换具有以下性质:
1.保持角的大小和方向不变;
2.把界面上的点映射到界面上的点;
3.把凸多边形映射为凸多边形;
4.对于给定的点z_0,存在唯一的茹科夫斯基保角变换f(z),将原凸多边形映射为目标凸多边形。

1 应用原理及特点在矿场水力压裂中,如何针对有效渗透率和厚 度不等的特定储层,设计出缝长和导流能力的优化 方案, 是应考虑的首要问题之一。
另外需要一种计算裂缝井产能的简易方法。
应用保角变换方法研究压裂井产能,其原理及特点是:①能将 z 平面上特别复杂的渗流问题转化为平面上一相对简单和易于求解的渗流问题;② 可准确地描述井筒附近较为复杂的流动型态( 裂缝 内流动和非裂缝区域拟径向流动) 对压裂后产能的贡献,而且能对不同导流能力造成的复杂流线型态 统一转化,因而具有广泛的适应性;③经过保角变换后假设的缝端封闭边界条件更符合实际,因保角变换后, 裂缝端部位于主流线上。
以此为基础,应用质量守衡定律和达西运动方程,推导出了裂缝内原油 流动所满足的压力二阶微分方程, 并进行了产量的 求解,与现有的典型曲线对比,一致性程度较好。
2 数学模型2、1模拟的假设条件 模拟的假设条件是: ①垂直裂缝 , 且对称分布于油井的两边; ②假设裂缝剖面为矩形, 高度恒定, 并等于油层厚度 ; ③裂缝宽度相对油藏的供给半径来 说非常小,即在进行保角变换时可忽略不记; ④裂缝 内导流能力可以是有限导流, 也可以是无限导流; ⑤油藏及裂缝内为单相流动,且符合达西线性定律; ⑥稳态渗流,且不考虑地层的垂向流动; ⑦不考虑地层和裂缝内的污染。
2、2模型 的建立在 z 平面上建立 一 Y 坐标系,保角变换转化为平面 r — s 坐标系( 图1 )图一 保角变换示意图取保角变换为:chw L z f =2ww e e chw -+=式中:z 为Z 平面上的复变函数,i y x z +=,f L 为裂缝半长,m;w 为变换后的W 平面,''i y x w +=。
裂缝井的渗流问题从而演变为带状地层向中心 线A 的单向渗流问题。
由于对称性 , 只研究 平 面中图示阴影部分的单向渗流问题。
其中'O 为''B A 的中点 , 即2''π=A O 。
§3.3 保角变换通过保角变换,把物理平面上的复杂几何域映射成像平面上的单位圆、半无限平面等简单规则域;同时把物理平面上的基本关系也用像平面上的复变量表示。
先在像平面的规则域上寻找满足这些基本关系的解,然后把结果返回物理平面就得到实际问题的解。
这种保角变换技术在下面介绍的级数展开法,柯西积分法以及解析延拓法中均能采用。
3.3.1 保角变换与曲线坐标 采用保角变换()ζω=z ,把弹性体在z 平面上所占的区域变换为ζ平面上的区域。
数学家已经进行了大量的研究,各种相应区域的保角变换解析函数)(ζω可从保角变换手册中查到。
在ζ平面上令θρθθρζi e i =+=)sin (cos , (3-17)式中ρ和θ是ζ点的极坐标(不是z 点的极坐标)。
ζ平面上的一个圆周const.ρ=和一根径向线const.θ=分别对应于z 平面上的一根曲线。
这两根曲线也就可以用const.ρ=和const.θ=来表示,如图3-3所示。
于是,ρ和θ是z 平面上一点的曲线坐标。
由于变换的保角性,这两组曲线总是正交的,相应的切线ρ和θ叫曲线坐标轴,它们的相对方向与坐标轴x 和y 相同。
设z 平面上有一个矢量F ,它的起点在()()i z e θωζωρ==。
F x 及F y 为这矢量在x 及y 轴上的投影,ρF 及θF 是它在ρ及θ轴上的投影。
设ρ轴与x 轴成角λ,则由几何关系有cos sin ,sin cos x y F F F F F F ρθρθλλλλ=-=+.于是可得()i x y F iF F iF e λρθ+=+即()i x y F iF F iF e λρθ-+=+ (1)为了求得λi e -,设想沿ρ轴方向给z 点以位移d z ,因而对应点ζ得径向位移d ζ,且d d , d d i i ze z e λθζζ==。
故()()()d ()d ()()d d i i ze e z λθωζζωζζωζρωζζωζωζ'''===='''⋅. (2)上式两边取共轭,得i e λ-,于是(1)式变为()()()x y F iF F iF ρθζωζρωζ'+=+' (3)3.3.2 保角变换后的位移与应力公式首先把其中z 的函数变换为ζ的函数。
目录1 保角变换的基本理论 (1)1.1 保角变换的定义 (1)1.2 保角变换的性质 (1)2 波导截止频率的计算 (2)2.1 分析方法 (3)2.2 保角变换结合矩量法求解波导截止频率 (3)3 总结 (5)参考文献 (6)保角变换法在波导截止频率计算中的应用保角变换法使用复变函数将复杂的边界变换为简单的容易求解的边界。
特别是对于二维有势场,由于其力线与等位线总是正交的,因而可以采用保角变换的方法将一个复杂的甚至是解析法无法描述的区域变换到一个易于用解析法描述的区域进行求解,同时,其边界可以与常用的坐标面重合,从而使边界条件变得较为简单直观。
比如将复杂的区域变换到矩形区域,且力线和等位线分别和坐标轴平行,以方便求解。
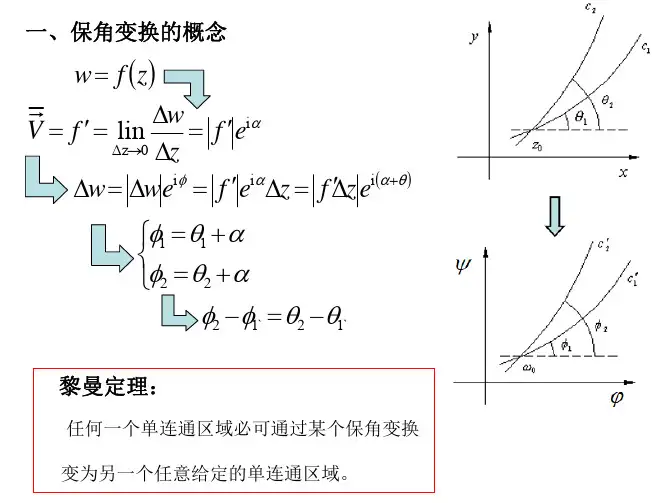
1 保角变换的基本理论1.1 保角变换的定义定义1 0arg '()f z 称为变换w=f(z)在点0z 的旋转角;0|'()|f z 称为变换w=f(z)在点0z 的伸缩率。
定义2 若对区域D 内任一点z ,变换w=f(z)具有性质:(1)保持角度不变,且旋转方向也不变;(2)保持伸缩率不变。
则称此变换w=f(z)在区域D 内为保角变换,也称变换w=f(z)在区域D 内保形。
如果在区域D 内点0z 的某一个邻域内变换w=f(z)具有性质(1)、(2),则称变换w=f(z)在点0z 的邻域内保形。
定理1 正则变换w=f(z),在每一个使'()0f z ≠的点z 的邻域内保形。
保形变换是正则变换的主要特征。
值得注意的是使'()0f z =的点0z ,也必然是变换w=f(z)在0z 处不保形。
但在保形变换中这种使变换w=f(z) 不保形的点,能帮助我们实现许多特殊区域的转化。
后面我们将会看到任何一个扇形区域到上半平面的变换恰好是利用幂变换在原点的不保形性来实现的。
1.2 保角变换的性质所谓保角变换或者叫做保形映照,是指通过一个解析函数w=f(z)将z 平面上的点变换为w 平面上的点。
叶轮测绘方格保角变换法绘型原理1. 引言叶轮测绘方格保角变换法是一种常用于工程测量中的绘图方法,它通过将实际尺寸放大或缩小到不同的比例尺上来制作工程图纸。
在这种方法中,方格保角变换法被广泛使用来处理平面图形的变形问题。
本文将详细解释叶轮测绘方格保角变换法的基本原理,包括方格保角变换法的概念、原理和步骤,并提供示例说明,以帮助读者更好地理解该方法。
2. 方格保角变换法的概念方格保角变换法是一种通过调整图形中各点之间的相对位置来实现尺寸缩放的方法。
它利用了平面几何中两个性质:等边比例和相似比例。
在进行方格保角变换时,我们首先将原始图形分割成一个个小方块(即方格),然后根据需要将每个小方块按照一定比例进行放大或缩小。
在此过程中,我们要求每个小方块内部的夹角大小保持不变。
通过这种方式,我们可以在不改变图形的形状的情况下,将其尺寸按比例调整到所需的大小。
3. 方格保角变换法的原理方格保角变换法的原理基于以下两个基本概念:等边比例和相似比例。
3.1 等边比例等边比例是指两条线段之间的长度比与其对应夹角之间的关系。
在平面几何中,如果两个三角形具有相等的夹角,并且它们对应边长之比相等,则称这两个三角形是等边比例的。
根据等边比例的性质,我们可以得出以下结论:在一个图形中,如果存在一条线段与另一条线段之间具有相等夹角,并且它们对应长度之比也相等,则这两条线段是等边比例的关系。
3.2 相似比例相似比例是指两个图形之间各对应部分长度之间的关系。
在平面几何中,如果两个图形具有完全相同的形状(即所有对应角度都相等),并且它们对应部分长度之比也相等,则称这两个图形是相似比例的。
根据相似比例的性质,我们可以得出以下结论:在一个图形中,如果存在一条线段与另一条线段之间具有相等夹角,并且它们对应长度之比也相等,则这两条线段所在的直线是相似比例的关系。
3.3 方格保角变换法的原理方格保角变换法利用了等边比例和相似比例的性质来实现图形尺寸的缩放。