保角变换和曲线坐标

f ( z0 ) 是经过映射Biblioteka f ( z ) 后通过点z0 的
的任何曲线C在 z0的伸缩率, 它与曲线C的形状及
方向无关. 所以这种映射又具有伸缩率的不变性.
5
2.共形映射（保角映射）
设函数w f ( z )在区域 D内解析, z0为 D内一点,
且 f ( z ) 0 , 那末映射w f ( z ) 在 z0 具有两个性 质: (1) 保角性; (2) 伸缩率不变性.
圆周的弧所围成的区域映射成一圆弧与一直线所 围成的区域. 3) 当二圆交点中的一个映射成无穷远点时, 这 二圆周的弧所围成的区域映成角形区域.
13
5. 几个初等函数所构成的映射
1) 幂函数 w z n ( n 2).
映射特点: 把以原点为顶点的角形域映射成以原
点为顶点的角形域, 但张角变成为原来的 n 倍.
故
b 1, a 1 i ,
(1 i ) z 1 ( i 1) z 1 所以 w 为所求. z (1 i ) z (1 i )
19
解3 利用典型区域映射公式
将所求映射设为 w e i
z z A , 1 z 1 z
保角变换
复变函数在几何意义上实际上相当于将平 面上的区域变成了平面上的另一个区域（简称 为映射）． 应用：利用复变函数（特别是解析函数）所构 成的映射来实现复杂区域的简单化，这将给实 际问题的研究带来很大的方便．而利用保角变 换法求解数学物理方程边值问题．
1
本章内容： 1）保角射的概念； 2）分式线性映射和几个初等函数所构成的 映射； 3）典型实例描述保角映射的应用． 重点： 分式线性变换及其映射特点 难点：

一、基础知识 1 定义在自变量域我们对同一个点从两个方向趋近，这两个趋近方向的夹角与在因变量上趋近的方向夹角一致，称为保角变换 2泊松方程与拉普拉斯方程对于泊松方程：20ρϕε∇=（在静电场中，可以表示电势与电荷的分布关系） 同时在没有电荷分布的地方满足拉普拉斯方程：20ϕ∇=3将在原来复杂的区域上的表达式通过一个变换，折射到宁一个区域上，使得某一分布函数得到简化变换的条件是泊松方程与拉普拉斯方程仍然成立22222x y∂∂∇=+∂∂，同时，我们定义x 、y 为ξ、η的函数：(,)x ξη、(,)y ξη 则x x x ξηξη∂∂∂∂∂=+∂∂∂∂∂2222222()x x x x x x x x x x ξηξξηηξηξξηη∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=+=+++ ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ 其中：222x x x x x ξηξηξξξηξξηξ ∂∂∂∂∂∂∂∂∂∂∂∂=⋅+=+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂ 同理：222x x x x x ηξηξηηηξηηξη∂∂∂∂∂∂∂∂∂∂∂∂=⋅+=+⋅ ∂∂∂∂∂∂∂∂∂∂∂∂∂ 所以：222222222222x x x x x x x ξηξηξηξηξηξη∂∂∂∂∂∂∂∂∂∂∂∂ =++++∂∂∂∂∂∂∂∂∂∂∂∂∂ 同理：222222222222y y y y y y y ξηξηξηξηξηξη∂∂∂∂∂∂∂∂∂∂∂∂=++++ ∂∂∂∂∂∂∂∂∂∂∂∂∂ 所以拉普拉斯方程变换为：22222222222222222222222x y x y x y xy xy x y y x ξξηηξξηηξηξηξηξηξη ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ ∇=+=+++++++++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂要满足保角变换，其实部与虚部都需要满足拉普拉斯方程：20ξ∇=、20η∇= 将实部与虚部要满足的拉普拉斯方程代入上式：2222222222222x y x y x y ξξηηξη∂∂∂∂∂∂∂∂ ∇=+=+++∂∂∂∂∂∂∂∂ ()'f z ix xξη∂∂=+∂∂（对于趋近方向为：0,0x y ∆→∆=） 222222"()f z x x x y y x ξηξξηη ∂∂∂∂∂∂=+=+=+ ∂∂∂∂∂∂将其代入：22222222'()'()'f z f z ξη ∂∂∇=+=∇∂∂也就是说，原坐标下的拉普拉斯方程与泊松方程变换为：220'0ϕϕ∇=⇒∇=222001''()f z ρρϕϕεε∇=⇒∇= 那么对于一个线段，在原坐标系下长度为1，其在新的坐标系下长度为'()f z 二、常用的保角变换1. 线性变换f az b =+，显然'f a =，其几何效果如下：线性变换一般不单独使用：仅对原来的二位分布做了位似2.幂和根式n xn f z = i n in z Ae f A e ϕϕ=⇒=用来处理过原点的射线，原来的射线的长度ρ的取值范围为（0，+∞），求幂或根还是（0，+∞）将原来的自变量求幂次积，几何效果如下：假设有变换3f z =，其效果为：将原来的60°夹角变为180°，并且其中的点的分布也随之扩大角度，假设原来的函数为电势分布函数，求p 点的电势，则通过变换之后，在新的复平面得到了一个平行分布的电势图，设新的电势分布图中，边界上的电势为V 0，则空间中的电势分布为0u V C η=+⋅，其中，C 为常数，C 与介质表面的面密度σ相关，其正负与σ的正负相反我们在新的复平面中求出电势的表达式之后，再求逆变换得到在原来的复平面上的电势表达式：0u V C η=+⋅中，由原来的变换：()()()32332322333(3)(3)i x iy x x iy x iy iy x xy i x y y ξη+=+=+⋅++=−+−由实部对实部，虚部对虚部，得：233x y y η=− 将η代入电势表达式中：()2303u V C x y y =+⋅−得到电势关于x 、y 的表达式同理可以得到将原来的复平面上的表达式开根得到将原来的夹角缩小相应的倍数的变换方法3. 指对数变换（一）、对于指数函数：()z x iy x iy f e e e e +===⋅此处需要注意，这里使用了复变函数的幅角表示法，即：i z Ae ϕ=，所以此处的x e 为幅值，iy e 为幅角其几何空间意义如下： （1），复平面中平行于实轴的直线，其变换后的图像为过原点的射线对于原空间有一条平行于实轴的直线（(,)y const x ∈−∞+∞，），原来的x 的值为幅角，y 的值为幅值。

从上面对于关系可以看出，w平面上半径为1的单位圆，对 应z平面上长度为2c的裂缝井。 再看w平面上任一圆（等势线）ρ=R，对应Z平面长轴为 c⎛ 1⎞ c 1 a = ⎜ R + ⎟ 短轴为： = ⎛ R − ⎞ 的椭圆。 b ⎜ ⎟ R⎠ 2⎝ R⎠ 2⎝
井径无穷小线段：rw = 假设： L ——
dz dw rw ρw ⇒ ρw = dw dz
z 平面上绕井封闭曲线； dn, dL —— z 平面上L的法线及切线单元； λ —— w平面对应封闭的曲线。 dv, d λ —— w平面上 λ 的法线及切线单元； Q —— z 平面上井产量；
Q =
∫
dφ dn
z
一个点
判断条件
z = z ( w) 单值 z = z ( w) 多值 z = z ( w) 单值 z = z ( w) 多值
根据以上对应关系，有以下逻辑判断成立： 如果单值 在一个平面上完成确定的流动网络（流场图）— —流线和等势线对应于另一个平面流动网络。此时 Φ ， Ψ 值本身是相同的 单值对应
z
w平面等势线 ρ = C2' 圆 w平面流线 θ = C2' 射线
7
保角变换及应用
寻求一个适当变换，把较复杂物平面问题变换为像平面问题，而像平面 复势，产量容易求出。待求出像平面产量公式后，再变换到物平面上。
例二：
直线供给边缘附近一口井。
8
保角变换及应用
取变换：w = ρ e
z 平面井心 w = 0 w平面原点 平面 z 点 x 上总有： = 0 y
w 平面上偏心井产量： Q =
q= 2π ( Φ e − Φ w ) ⎡ πL ⎛ ρa ρ e ln ⎢ e ⋅ e a ⋅ ⎜1 − e 2 ⎢ πρ r ⎜ ρe e w ⎜ ⎢ ⎝ ⎣

（11.1.3）
利用解析函数
的C-R条件
(11.1.4)
以及解析函数的实部和虚部分别满足拉普拉斯方程的性质
(11.1.5)
将式（11.1.4）和式（11.1.5）代入到式（11.1.3）化简后得到
注意到上式已经使用了：
对于保角变换
满足拉普拉斯方程，则
因而只要 ）也满足拉
普拉斯方程，即为
（11.1.6）
(11.1.9) 经变换后仍然服从亥姆霍兹方程 (11.1.10)
注意到方程要比原先复杂，且 能不是常系数．
前的系数可
保角变换法的优点不仅在于拉普拉斯方程、泊松方程
等方程的类型在保角变换下保持不变，更重要的是，能将
复杂边界问题变为简单边界问题，从而使问题得到解决．
保角变换的特点



角度不变； 方程形式不变； 电势不变； 总电荷不变； 电容不变；
角变换法求解．
保角变换法解定解问题的基本思想：
通过解析函数的变换或映射（这部分知识在复变函数论中 已经学习过）将 Z平面上具有复杂边界形状的边值问题变换为 W平面上具有简单形状（通常是圆、上半平面或带形域）的
边值问题，而后一问题的解易于求得．于是再通过逆变换
就求得了原始定解问题的解． 这就是本章将要介绍的一种解决数学物理方程定解 问题中的解析法――保角变换法，
z平面
x
y
z平面
x

x
（8）儒阔夫斯基变换 取 式中A、a均为常数，此式可改写为 得
＝常数，对应椭圆，焦点为 ＝常数，对应双曲线，焦点为 ，对应两条射线； ，对应一个线段。
将t和z分别写成实部和虚部的形式，便可以证 明，此变换能将t平面实轴上大于 和小于 部分变换为z平面的实轴；而t平面实轴上 一段 则变换到z平面上，成为圆心在z＝0， 半径为a的一个圆。

§ 8.7 保角变换和曲线坐标学习思路：弹性力学问题的求解有赖于边界条件的简化。

对于复杂的边界形状，如果利用空间的变换，将是简化问题求解的最好途径。

保角变换就是充分发挥复变函数的特长，将孔口问题映射到平面的单位圆。

这一节将介绍保角变换和曲线坐标的概念。

由于应用保角变换，矢量－位移，张量－应力公式以及K-M 函数等均必须做出曲线坐标描述。

保角变换使得问题的公式复杂，但是边界条件的简化，以及柯西积分的应用将简化问题的分析。

在本节学习之前，请你先学习附录2，（有关保角变换的知识）学习要点：1.保角变换和曲线坐标；2.矢量的保角变换；3.位移分量的曲线坐标表达式；4.应力分量的曲线坐标表达式。

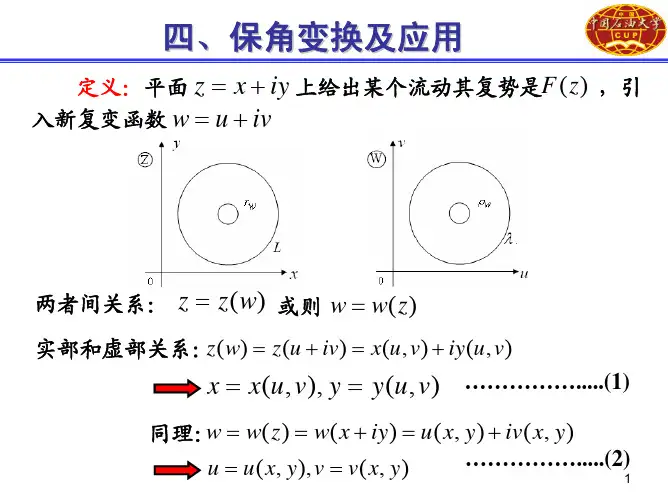
为了便于根据边界条件确定 K-M 函数，采取保角变换z = （）将物体在z 平面上所占的区域变为在平面所占的区域。

一般的说，通过保角变换可以将非圆边界映射为圆边界，使得问题得以简化。

假设将z 平面上的有限区域或者无限区域S 映射为平面的单位圆内的区域，并且将z 平面上的区域S的边界l 映射为单位圆，对应的关系如下表：由于平面上的任一点可以表示为，。

和是点的极坐标。

而根据保角变换公式z = ( )，则z平面任意一点也可以通过和表示。

因此，和又称为曲线坐标。

对于某些问题的描述中，采用曲线坐标形式表示位移和应力有利于问题的分析。

曲线坐标的概念：平面的一个圆周=const 和一条径向直线=const分别对应于z 平面的两条曲线，这两条曲线就记作=const和=const。

于是和可以看作z 平面上一点的曲线坐标。

由于变换的保角性，这个曲线坐标总是正交的，而且坐标轴和的相对位置和坐标轴Ox和Oy的相对位置相同，如图所示。

首先讨论矢量的保角变换。

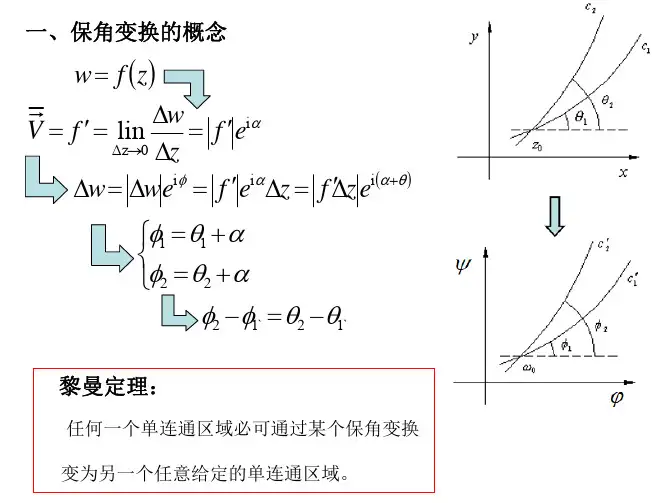
设曲线坐标，即=const 与x 轴夹角，如果A 为z 平面上的任一矢量，设A 与曲线坐标夹角。

设A x, A y 分别表示矢量A 在x，y 轴的投影；A , A 表示在=const 和=const 上的投影，则上式的几何意义为，将矢量A 绕z 点顺时针方向转动角后，其在Oxy 坐标系的位置，相当于A 在曲线坐标系( ， )中的位置，如图所示。

比较结果如表 2-1 所示
从表 2-1 可见
为节约计算时间
本文 Laplace 数值逆变换中的
2.1.2 Hankel 变换及数值逆变换 1 Hankel 变换及逆变换式为
~m
f (ξ) = H m ( f ( r )) = ∫ rf (r ) J m (ξr ) dr
0 ~m ∞ ~m
∞
2.22
f (r) = H
1 a +i ∞ st f (t ) = L [ F ( s )] = ∫i∞F (s )e ds 2πi a −
−1
(2.2)
Heaviside 阶跃函数
形状如图 2-1 所示 t<0 t 0 f(t) 1 (2.3)
H (t ) =
f(t) 1
0 1
t
图 2-1 H(t) 阶跃函数
a
图 2-2 Fig.2-2 -13-
其中
−1
m
( f (ξ)) = ∫ ξ f (ξ) J m (ξr )dξ
0
(2.23)
J m (ξr ) 是第一类 m 阶 Bessel 函数. 1 ' m f (r ) − 2 f ( r )] = −ξ 2 H m [ f (r )] r r ξ (( m − 1) H m +1 [ f (r )] − ( m + 1) H m −1 [ f ( r )]) 2m
(2)Hankel 变换的性质有
H m [ f '' ( r ) + H m [ f ' ( r )] =
2.24 (2.25) (2.26)
1 ξ H m [ f ( r )] = ( H m −1 [ f (r )] + H m +1 [ f ( r )]) r 2m

d w dW d d z d d z
在无穷远处，有：
d w d z
dW d
d dz
考虑到
dW d
kV
，
d dz
1 k
，有：
dw dz
V
三、环量的确定
1. 补充条件
dw 有限的常数
dz zB 2. 环量的确定
dz
d
E
0
dw 有限常数
dz zB
dw
d
E
w1 z
Q
2
lnz
i
h
Q
2
lnz
i
h
Q ln z2 h2 2
wz
w1 z
w1
a2 z
wz
Q
2
ln z2
a4 z2
h2
a4 h2
dz
d
k
；（其中：
k
是正的实数）
（根据黎曼定理这样的函数存在且是唯一的）
W
kV
w
z
kV R
kV
2
2 i
F z
ln
kV
F z
R
2
F z
ln
2 i
F
z
证明：1. 因W 是在 K D 上连续且在 D 内解析的函数， Fz是在 C D 上连续且在 D 内解析的函数。于是，根据复合函数的性质 wz W F z
一、保角变换的概念
w f z
V f lin w f ei Δz0 z
w wei f eiz f z ei
12
1 2
2 1` 2 1`
黎曼定理：
任何一个单连通区域必可通过某个保角变换 变为另一个任意给定的单连通区域。

1 应用原理及特点在矿场水力压裂中，如何针对有效渗透率和厚 度不等的特定储层，设计出缝长和导流能力的优化 方案， 是应考虑的首要问题之一。

另外需要一种计算裂缝井产能的简易方法。

应用保角变换方法研究压裂井产能，其原理及特点是：①能将 z 平面上特别复杂的渗流问题转化为平面上一相对简单和易于求解的渗流问题；② 可准确地描述井筒附近较为复杂的流动型态( 裂缝 内流动和非裂缝区域拟径向流动) 对压裂后产能的贡献，而且能对不同导流能力造成的复杂流线型态 统一转化，因而具有广泛的适应性；③经过保角变换后假设的缝端封闭边界条件更符合实际，因保角变换后， 裂缝端部位于主流线上。

以此为基础，应用质量守衡定律和达西运动方程，推导出了裂缝内原油 流动所满足的压力二阶微分方程， 并进行了产量的 求解，与现有的典型曲线对比，一致性程度较好。

2 数学模型2、1模拟的假设条件 模拟的假设条件是： ①垂直裂缝 ， 且对称分布于油井的两边； ②假设裂缝剖面为矩形， 高度恒定， 并等于油层厚度 ； ③裂缝宽度相对油藏的供给半径来 说非常小，即在进行保角变换时可忽略不记； ④裂缝 内导流能力可以是有限导流， 也可以是无限导流； ⑤油藏及裂缝内为单相流动，且符合达西线性定律； ⑥稳态渗流，且不考虑地层的垂向流动； ⑦不考虑地层和裂缝内的污染。

2、2模型 的建立在 z 平面上建立 一 Y 坐标系，保角变换转化为平面 r — s 坐标系( 图1 )图一 保角变换示意图取保角变换为：chw L z f =2ww e e chw -+=式中：z 为Z 平面上的复变函数，i y x z +=，f L 为裂缝半长，m;w 为变换后的W 平面，''i y x w +=。

裂缝井的渗流问题从而演变为带状地层向中心 线A 的单向渗流问题。

由于对称性 ， 只研究 平 面中图示阴影部分的单向渗流问题。

其中'O 为''B A 的中点 ， 即2''π=A O 。

保角变换能计算力摘要：1.保角变换的定义和作用2.保角变换在计算力中的应用3.保角变换在实际问题的应用案例4.保角变换的局限性和发展前景正文：保角变换是一种数学变换，它在数学、物理等领域具有广泛的应用。

保角变换能够保持角度不变，仅改变长度和面积的比值。

在计算力方面，保角变换能够简化复杂的计算问题，提高计算效率。

保角变换在计算力中的应用主要体现在以下几个方面：1.坐标变换：在平面上，保角变换可以将一个复杂的图形变换到一个简单的图形，从而降低问题的复杂度。

例如，将极坐标变换为直角坐标，可以简化计算过程。

2.微积分：在求解微分方程、积分等问题时，保角变换可以将复杂的问题转化为简单的三角函数问题。

例如，在研究波动方程时，利用保角变换可以将空间坐标变换为复数坐标，从而简化问题的求解。

3.数值计算：在数值计算中，保角变换可以提高计算精度和稳定性。

例如，在求解非线性方程时，采用保角变换可以将方程变为易于求解的形式。

4.信号处理：在信号处理领域，保角变换被广泛应用于信号分析、滤波和信号重建。

例如，傅里叶变换和拉普拉斯变换就是两种常见的保角变换方法，它们能够将时域信号转换为频域信号，从而方便对信号进行分析和处理。

在实际问题中，保角变换的应用案例众多。

例如，在地震勘探、无线通信、图像处理等领域，保角变换技术都发挥着重要作用。

然而，保角变换也存在一定的局限性，如在处理奇异值问题时，保角变换可能失效。

因此，在未来发展中，我们需要不断探索新的变换方法，以应对更为复杂的问题。

总之，保角变换在计算力领域具有重要的应用价值。

通过简化复杂问题、提高计算效率，保角变换为科学研究和实际工程带来极大的便利。

[平衡微分方程的适用范围]平衡微分方程平衡微分方程的适用范围弹性力学、塑性力学、弹塑性力学。

张量:怎样判断？商判则：和任意矢量点积为K-1阶张量的量一定为K 阶张量。

能否满足分量转换规律是判断某个数的集合是否表示一个张量的基本准则。

3、n 维张量的举例标量零阶张量，矢量为一阶张量，应力、应变为二阶张量，应力、应变之间的弹性关系可用四阶张量表示。

4、▽的意义？▽为一个梯度，▽2为调和算子，▽4为重调和算子。

5、柯西应变张量与格林应变张量的区别？柯西应变张量适用于线弹性小变形，格林应变张量适用于任何情况。

6、任意斜面上的应力的本质是？平衡微分方程和转轴公式。

7、如何描述正应变，剪应变，体积应变，应力的球张量，应力的偏张量？对于各向同性材料，正应力引起正应变，引起线元长度变化；剪应力引起剪应变，引起角度的变化；应力的球张量，只引起体积变化，不会引起形状的变化；应力的偏张量，只引起形状变化，不会引起体积的变化。

动力学的平衡微分方程如何表示？根据达朗贝尔原理，把惯性力当作体力来满足力平衡和力矩平衡条件。

9、转轴公式的理论依据:柯西公式。

10、等效应力、等效应变物理意义、公式：等效应力将6个应力分量的对变形体的作用，等效于一个单向拉伸力的作用；等效应变将6个应变分量等效于一个单向拉伸力所产生的应变。

利用实验，就可以直接建立等效应变与等效应力的数值关系11、体积不可压：从体积弹性模量来看，当时，K 趋向于无穷大，也就是说体积变化无限小，即表示体积不可压缩。

12、为什么等值拉压是纯剪切等值拉压时，线元只有角度发生变化，长度有发生变化，故等值拉压是纯剪切。

13、里茨和伽辽金法的物理思想均是利用利用最小势能原理，寻找满足约束边界条件的试验函数。

14、弹性力学为什么可用逆解法、半逆解法：解的唯一性定理表明，无论用什么方法求得的解，只要能满足全部基本方程和边界条件，就一定是问题的真解。

15、叠加原理建立在什么条件下：基本方程和边界条件满足线弹性条件，举例：在线弹性条件下，复杂问题可通过简单叠加处理。

§3.3 保角变换通过保角变换，把物理平面上的复杂几何域映射成像平面上的单位圆、半无限平面等简单规则域；同时把物理平面上的基本关系也用像平面上的复变量表示。

先在像平面的规则域上寻找满足这些基本关系的解，然后把结果返回物理平面就得到实际问题的解。

这种保角变换技术在下面介绍的级数展开法，柯西积分法以及解析延拓法中均能采用。

3.3.1 保角变换与曲线坐标 采用保角变换()ζω=z ，把弹性体在z 平面上所占的区域变换为ζ平面上的区域。

数学家已经进行了大量的研究，各种相应区域的保角变换解析函数)(ζω可从保角变换手册中查到。

在ζ平面上令θρθθρζi e i =+=)sin (cos ， (3-17)式中ρ和θ是ζ点的极坐标(不是z 点的极坐标)。

ζ平面上的一个圆周const.ρ=和一根径向线const.θ=分别对应于z 平面上的一根曲线。

这两根曲线也就可以用const.ρ=和const.θ=来表示，如图3-3所示。

于是，ρ和θ是z 平面上一点的曲线坐标。

由于变换的保角性，这两组曲线总是正交的，相应的切线ρ和θ叫曲线坐标轴，它们的相对方向与坐标轴x 和y 相同。

设z 平面上有一个矢量F ，它的起点在()()i z e θωζωρ==。

F x 及F y 为这矢量在x 及y 轴上的投影，ρF 及θF 是它在ρ及θ轴上的投影。

设ρ轴与x 轴成角λ，则由几何关系有cos sin ,sin cos x y F F F F F F ρθρθλλλλ=-=+.于是可得()i x y F iF F iF e λρθ+=+即()i x y F iF F iF e λρθ-+=+ (1)为了求得λi e -，设想沿ρ轴方向给z 点以位移d z ，因而对应点ζ得径向位移d ζ，且d d , d d i i ze z e λθζζ==。

故()()()d ()d ()()d d i i ze e z λθωζζωζζωζρωζζωζωζ'''===='''⋅. (2)上式两边取共轭，得i e λ-，于是(1)式变为()()()x y F iF F iF ρθζωζρωζ'+=+' (3)3.3.2 保角变换后的位移与应力公式首先把其中z 的函数变换为ζ的函数。

2.4 曲面域的面积
D
v v ) P3 (u u, v v ) ru u
P1 (u u, v ) P ( u, v ) PP 1 r ( u u, v ) r ( u, v ) ( ru 1 )u ru u. ( u 0时) PP2 r (u, v v ) r (u, v ) (rv 2 )v rv v. (v 0时) PP 1 PP 2 d ru u rv v ru rv dudv
曲纹坐标方程有关，不 需要知道曲线的形状 .
2.2 曲面上两方向的交角
( S )在点P (u, v )处的两个切方向 定义 已给曲面 称相应的切向量 (d ) du : dv和( ) u : v， dr rudu rv dv和r ruu rvv 之间的夹角 为这两个切方向 (d )和( )之间的夹角 .(0 ) 计算公式 dr r dr r cos , dr r ( ru du rv dv) ( ruu rvv ) cos 2 dr r ( ru du rv dv) ( ruu rvv ) 2
则ds Edu 2Fdudv Gdv .
2 2 2
称为曲面的第一基本形 式. 记作I .
即
其中
I Edu 2Fdudv Gdv 2 2 E ru , F ru rv , G rv
2
2
称为曲面的第一类基本 量. 对于曲面S : z z( x, y )， 有r { x, y, z( x, y)} ， z z 于是rx {1,0, p}， ry {0,1, q}， 其中p ，q ， x y 2 2 2 2 E rx 1 p , F rx ry pq, G ry 1 q .

在处理波动方程中的应用
波动方程是描述波动现象的基本方程，如声波、光波等。保 角变换在处理波动方程中具有广泛应用。
通过保角变换，可以将波动方程转化为更容易求解的形式， 如分离变量法或积分变换法等。这有助于我们更深入地理解 波动现象的本质，并为实际工程问题提供解决方案。
在研究几何光学问题中的应用
几何光学是研究光线传播规律的科学。保角变换在几何光 学中有重要应用，尤其是在处理光线折射和反射问题时。
02
常见的保角变换方法
极坐标变换
01
02
03
极坐标变换是一种常见 的保角变换方法，它将 平面上的点从直角坐标
系变换到极坐标系。
极坐标变换公式为：$x = rcostheta, y =
rsintheta$，其中$r$是 点到原点的距离，
$theta$是点与x轴的夹角。
极坐标变换在处理与圆 和极坐标相关的问题时 非常有用，例如电场、 磁场和流体力学中的问
发展高维空间的保角变换
将保角变换从二维平面扩展到高维空间，探索其在高维几何处理和 计算几何等领域的应用。
保角变换的算法优化与改进
算法效率提升
针对现有保角变换算法的瓶颈，研究优化算法结构和计算 过程，提高算法执行效率。
并行化与分布式计算
利用并行化和分布式计算技术，实现大规模保角变换任务 的快速处理和实时响应。
弹性力学中的保角变换在结构分析、地震工程和材料科学等领
03
域有广泛应用。
03
保角变换在数学物理问题 中的应用
在求解偏微分方程中的应用
偏微分方程是描述物理现象的重要工具，而保角变换可以用来求解某些偏微分方 程。通过保角变换，可以将复杂的偏微分方程转化为更容易求解的形式，从而得 到物理现象的解。

dw b 容易验证：分式线性映射的逆映射 z ， cw a (a)(d ) bc 0 也是分式线性映射，因此，我们通常也把分
式线性映射称为双线性映射．
dw ad bc 由于分式线性映射的导数 0 ，因而， 2 dz cz d
分式线性映射是保角映射． 容易验证 ： 两个分式线性映射的复合仍是一个分式线性 映射． 事实上，设
定理 6.2.4 在 z 平面和 w 平面上任意给定三个相异的点 z1 ，
az b 【证明】 设 w cz d w k k 1, 2,3 ，即
2， 3 1，
wk
于是
az b azk b z zk ad bc w wk cz d czk d cz d czk d
azk b czk d
2， 3 ， k 1，
k 1， 2
az3 b azk b z3 zk ad bc w3 w k cz3 d czk d cz3 d czk d
由此可得
2 k 1，
w w1 w 3 w 2 z z1 z3 z2 w w 2 w 3 w1 z z2 z3 z1
6.1 保角映射的概念
我们在讨论解析函数导数的几何意义时已经提到了保角映射这 一概念．
6.1.1 保角映射的概念
定义 6.1.1 为保角映射． 凡具有保角性（角度相同，旋转方向相同）和伸缩率不变性的映 射称为第一类保角映射． 凡具有保角性(角度相同但旋转方向相反 )和伸缩率不变性的映射 称为第二类保角映射． 保角映射 凡具有保角性和伸缩率不变性的映射称
az b 设w ，可以把它化为 cz d ad 1 a (6.2.1) w b c cz d c 1 B （ A ， B 为复常数） 令 cz d ， ，那么 w A ．

1
()
1
() ()
1
()
1
2πi
−
+ 2πi
− ( ) + 2πi
−
= 2πi
−
l ( )=∑
在圆外域是解析的
l 位于圆内域
l ( )在圆内域是解析的 l 位于圆内域
1()2πi−源自= (∞) = +
∞ =0
1
()
2πi
−
= ()
(
)
=
−
1 2πi
() ()
1
− ( ) + 2πi
−
上表中的 ( )和 ( )的表达式的右端第一项与变换函数 ( )（即孔的形状）有关，称几何项。第二项与孔边和远 方的外力有关，称为载荷项。
B. 复杂情况求数值解 方法 1
→ →
(如：上面 4 种级数形式的映射关系就没办法逆映射)：
(1) 先把应力组合转到像空间，
⎧ + = 2 ( ) + ( ) = 4Re[ ( )]
⎪ − +2
= ( ) 2[ ̅ ( ) + ( )]
(5)
⎨
⎪ ⎩
2
[
+
]＝
( )−
() ()
( )− ( )
并利用像平面中解得的 ( ), ( )求解应力和位移分量，即分别得到了 (ξ, η)~
接下来就可以利用 4.5 节介绍的复数级数方法，来求解单位圆域的 ( )和 ( )。我们只需要用将 平面 K-M 函数的 级数代入(2)式左边，并把右边已知外力也在 平面展开成 F 级数，比较左右两边的系数就可求解。
2/5
Email:onexf@

§1 复变函数的定义由两个实数x，y确定的数z=x+i y称为复数。

x，y分别称为复数z的实部和虚部，记作x=Re z 和y =Im z。

Re和Im分别为表示复数实部和虚部的符号。

其中称为虚数单位。

显然z可以用直角坐标系（x，y）表示，x称为实轴，y称为虚轴。

坐标平面称为复平面，或者z平面。

因此，z平面上的任一点可记作称为复数z的模，称为z的幅角，其在[0，2 ]之间的值称为主幅角。

显然，复数可以写作极坐标表达形式。

设有一个复数z=x+i y的集合g。

对于集合g中的每一个复数z都有对应的复数值，w=u+i v，则称w是z的复变函数，记作w = f (z)。

给定一个复变函数就是在点（x，y）与（u，v）之间给出了一一对应关系。

因此，u，v均随x，y而确定，这就是说给定了一个复变函数和给定两个实变函数u=u（x，y），v=v（x，y）是等价的。

而且w=u（x，y）+i v（x，y）复变函数和实变函数同样有单值函数和多值函数，应该注意到实变函数的性质对于复变函数可能是不成立的。

例如复变函数中的对数函数w=ln z是多值的。

为了便于理解，以对数函数为例。

设。

上式对于z的所有不等于零的复数值定义了函数ln z。

在公式中包含一个任意的整数k，这就是说ln z是一个多值函数。

对于k的任一整数值，就有函数ln z的一个分支。

通常取k=0的那一支叫做的主值，即如果z的一个值对应着w的一个值，那么函数f（z）是单值函数；如果z的一个值对应着两个或两个以上的w值，则f（z）是多值函数。

集合g称为f（z）的定义集合。

§2 解析函数--复变函数的可导性复变函数的导数与实变函数的导数定义是相同的。

因此，关于实变函数的一系列微分公式与法则，可以完全照搬到复变函数上。

不过应该注意的是，复变函数的变量是复变量，不是实变量。

值得指出的是，实变函数的可导性要求当x＝x0+∆x 由左右两方趋近x0时，∆y/∆x的极限都存在而且相等。

式 中 t = 2 y max
式中b 式中 —— 弦长
1.4.P13
对于 ζ 平面绕圆流动有复位势
a 2 iα iΓ ζ + m W (ζ ) = ∞ (ζ + m ) e − iα + e − ln a ζ + m 2π
可由此求得 W ( z )。 环量为 Γ = −4π
∞
c (1 + ε ) sin α
ζ 平面上圆心在虚轴
上，距原点 m
c，
且过 ζ = ±c 两点的圆， 两点的圆， 可变换为 z 平面上的 圆弧，如图，方程为 圆弧，如图，
c c2 x2 + y + = c2 4 + 2 m m
2 2
1.4.P15
弦长为 b=4c ，顶点 f=2m。 。 在 z 平面上，以 b 和 f 表示其方程为 平面上，
2
平板升力为 升力系数为
L = πρ
2
∞
b sin α
Cl = 2π sin α
1.4.P11
（四）对称翼型（儒可夫斯基舵）绕流 对称翼型（儒可夫斯基舵）
ζ
平面上，圆心在横轴上原点左面，离原点 平面上，圆心在横轴上原点左面，
m<<c ，过 ζ = +c 的圆 ，经变换后得 z 平面上 的对称翼型。 的对称翼型。
dζ )
V
(z )
若 ζ 平面上来流复速度为
V (ζ ) =
∞ζ
e
− iα ζ
则 z 平面上来流复速度为
dz V ( z )( )ζ → ∞ = dζ
∞
e
− iα ζ
1.4.P4
（三）流动奇点强度在保角变换中的变化 作保角变换时，二平面上的点涡、 作保角变换时，二平面上的点涡、点源强度有 关系