下载文档原格式
§4保角映射的物理应用拉普拉斯方程式02=∇φ为工程数学中最重要偏微分方程式之一，因为它应用于有关重力场、静电场、稳态热传导以及不可压缩流体之流动问题．本文所及者皆为二维问题，它们虽原三维空间内之物理系统，但是诸如位势中与空间第三坐标无关，因此拉普拉斯方程为022222=∂∂+∂∂=∇=∆yx φφφφ（1）称曲线=),(y x φ常数为等位线．定义1对于区域G 内的实值函数),(y x φ（或)(z φ），如果其本身以及一阶、二阶偏导数连续而且满足（1），则称φ在G 内调和或φ是区域G 的调和函数．注意：对于定义中调和函数的光滑性要求可以减弱。
可以说明调和性是共性映射（保角映射）下的不变性质，因为若)(ζz z =是区域D 到G 的共性映射，记))(()(ζζz u U =，不难验证：)()()(2z u z U ∆'=∆ζζ．因此，若)(z u 在G 内调和，必有)(ζU 在D 内调和．定义2设)(z u 和)(z v 在区域G 内调和，如果x y y x v u v u -==,，则称)(z v 是)(z u 的共轭调和函数．称dy u dx u du x y +-=*为dy u dx u du y x +=的共轭微分．理论上说，一个调和函数的共轭函数的存在性虽有待讨论，但其共轭微分总是有意义的．定理1若)(z u 是单连通区域G 内的调和函数，则其共轭调和函数)(z v 一定存在，因此为)()()(z iv z u z f +=G 内的解析函数． 证明例2已知调和函数22(,)u x y x y xy =-+，求其共轭调和函数(,)v x y 及解析函数()(,)(,)f z u x y i v x y =+.解利用C-R 方程，(2)2v u y x y x x y∂∂=-=--+=-∂∂ 所以2(2)2()2x v y x dx xy g y =-=-+⎰.因此，2()vx g y y ∂'=+∂2u x y x∂==+∂， 比较两式可得：2()2,()x g y x y g y y ''+=+=故，有2()2y g y ydy C ==+⎰.因此，22222x y v xy C =-++。
目录1 保角变换的基本理论 (1)1.1 保角变换的定义 (1)1.2 保角变换的性质 (1)2 波导截止频率的计算 (2)2.1 分析方法 (3)2.2 保角变换结合矩量法求解波导截止频率 (3)3 总结 (5)参考文献 (6)保角变换法在波导截止频率计算中的应用保角变换法使用复变函数将复杂的边界变换为简单的容易求解的边界。
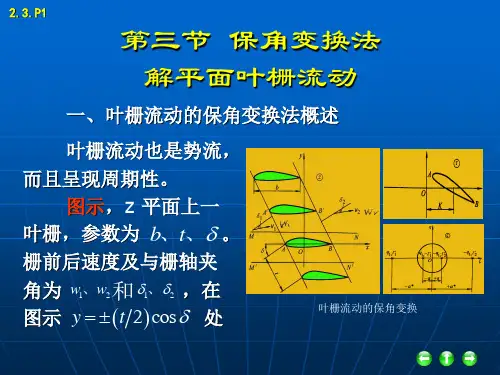
特别是对于二维有势场，由于其力线与等位线总是正交的，因而可以采用保角变换的方法将一个复杂的甚至是解析法无法描述的区域变换到一个易于用解析法描述的区域进行求解，同时，其边界可以与常用的坐标面重合，从而使边界条件变得较为简单直观。
比如将复杂的区域变换到矩形区域，且力线和等位线分别和坐标轴平行，以方便求解。
1 保角变换的基本理论1.1 保角变换的定义定义1 0arg '()f z 称为变换w=f(z)在点0z 的旋转角；0|'()|f z 称为变换w=f(z)在点0z 的伸缩率。
定义2 若对区域D 内任一点z ，变换w=f(z)具有性质：（1）保持角度不变，且旋转方向也不变；（2）保持伸缩率不变。
则称此变换w=f(z)在区域D 内为保角变换，也称变换w=f(z)在区域D 内保形。
如果在区域D 内点0z 的某一个邻域内变换w=f(z)具有性质（1）、（2），则称变换w=f(z)在点0z 的邻域内保形。
定理1 正则变换w=f(z)，在每一个使'()0f z ≠的点z 的邻域内保形。
保形变换是正则变换的主要特征。
值得注意的是使'()0f z =的点0z ，也必然是变换w=f(z)在0z 处不保形。
但在保形变换中这种使变换w=f(z) 不保形的点，能帮助我们实现许多特殊区域的转化。
后面我们将会看到任何一个扇形区域到上半平面的变换恰好是利用幂变换在原点的不保形性来实现的。
1.2 保角变换的性质所谓保角变换或者叫做保形映照，是指通过一个解析函数w=f(z)将z 平面上的点变换为w 平面上的点。
