保角变换法求解定解问题
- 格式:ppt
- 大小:652.00 KB
- 文档页数:36








一、基础知识 1 定义在自变量域我们对同一个点从两个方向趋近,这两个趋近方向的夹角与在因变量上趋近的方向夹角一致,称为保角变换 2泊松方程与拉普拉斯方程对于泊松方程:20ρϕε∇=(在静电场中,可以表示电势与电荷的分布关系) 同时在没有电荷分布的地方满足拉普拉斯方程:20ϕ∇=3将在原来复杂的区域上的表达式通过一个变换,折射到宁一个区域上,使得某一分布函数得到简化变换的条件是泊松方程与拉普拉斯方程仍然成立22222x y∂∂∇=+∂∂,同时,我们定义x 、y 为ξ、η的函数:(,)x ξη、(,)y ξη 则x x x ξηξη∂∂∂∂∂=+∂∂∂∂∂2222222()x x x x x x x x x x ξηξξηηξηξξηη∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=+=+++ ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ 其中:222x x x x x ξηξηξξξηξξηξ ∂∂∂∂∂∂∂∂∂∂∂∂=⋅+=+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂ 同理:222x x x x x ηξηξηηηξηηξη∂∂∂∂∂∂∂∂∂∂∂∂=⋅+=+⋅ ∂∂∂∂∂∂∂∂∂∂∂∂∂ 所以:222222222222x x x x x x x ξηξηξηξηξηξη∂∂∂∂∂∂∂∂∂∂∂∂ =++++∂∂∂∂∂∂∂∂∂∂∂∂∂ 同理:222222222222y y y y y y y ξηξηξηξηξηξη∂∂∂∂∂∂∂∂∂∂∂∂=++++ ∂∂∂∂∂∂∂∂∂∂∂∂∂ 所以拉普拉斯方程变换为:22222222222222222222222x y x y x y xy xy x y y x ξξηηξξηηξηξηξηξηξη ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ ∇=+=+++++++++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂要满足保角变换,其实部与虚部都需要满足拉普拉斯方程:20ξ∇=、20η∇= 将实部与虚部要满足的拉普拉斯方程代入上式:2222222222222x y x y x y ξξηηξη∂∂∂∂∂∂∂∂ ∇=+=+++∂∂∂∂∂∂∂∂ ()'f z ix xξη∂∂=+∂∂(对于趋近方向为:0,0x y ∆→∆=) 222222"()f z x x x y y x ξηξξηη ∂∂∂∂∂∂=+=+=+ ∂∂∂∂∂∂将其代入:22222222'()'()'f z f z ξη ∂∂∇=+=∇∂∂也就是说,原坐标下的拉普拉斯方程与泊松方程变换为:220'0ϕϕ∇=⇒∇=222001''()f z ρρϕϕεε∇=⇒∇= 那么对于一个线段,在原坐标系下长度为1,其在新的坐标系下长度为'()f z 二、常用的保角变换1. 线性变换f az b =+,显然'f a =,其几何效果如下:线性变换一般不单独使用:仅对原来的二位分布做了位似2.幂和根式n xn f z = i n in z Ae f A e ϕϕ=⇒=用来处理过原点的射线,原来的射线的长度ρ的取值范围为(0,+∞),求幂或根还是(0,+∞)将原来的自变量求幂次积,几何效果如下:假设有变换3f z =,其效果为:将原来的60°夹角变为180°,并且其中的点的分布也随之扩大角度,假设原来的函数为电势分布函数,求p 点的电势,则通过变换之后,在新的复平面得到了一个平行分布的电势图,设新的电势分布图中,边界上的电势为V 0,则空间中的电势分布为0u V C η=+⋅,其中,C 为常数,C 与介质表面的面密度σ相关,其正负与σ的正负相反我们在新的复平面中求出电势的表达式之后,再求逆变换得到在原来的复平面上的电势表达式:0u V C η=+⋅中,由原来的变换:()()()32332322333(3)(3)i x iy x x iy x iy iy x xy i x y y ξη+=+=+⋅++=−+−由实部对实部,虚部对虚部,得:233x y y η=− 将η代入电势表达式中:()2303u V C x y y =+⋅−得到电势关于x 、y 的表达式同理可以得到将原来的复平面上的表达式开根得到将原来的夹角缩小相应的倍数的变换方法3. 指对数变换(一)、对于指数函数:()z x iy x iy f e e e e +===⋅此处需要注意,这里使用了复变函数的幅角表示法,即:i z Ae ϕ=,所以此处的x e 为幅值,iy e 为幅角其几何空间意义如下: (1),复平面中平行于实轴的直线,其变换后的图像为过原点的射线对于原空间有一条平行于实轴的直线((,)y const x ∈−∞+∞,),原来的x 的值为幅角,y 的值为幅值。
§ 8.7 保角变换和曲线坐标学习思路:弹性力学问题的求解有赖于边界条件的简化。
对于复杂的边界形状,如果利用空间的变换,将是简化问题求解的最好途径。
保角变换就是充分发挥复变函数的特长,将孔口问题映射到平面的单位圆。
这一节将介绍保角变换和曲线坐标的概念。
由于应用保角变换,矢量-位移,张量-应力公式以及K-M 函数等均必须做出曲线坐标描述。
保角变换使得问题的公式复杂,但是边界条件的简化,以及柯西积分的应用将简化问题的分析。
在本节学习之前,请你先学习附录2,(有关保角变换的知识)学习要点:1.保角变换和曲线坐标;2.矢量的保角变换;3.位移分量的曲线坐标表达式;4.应力分量的曲线坐标表达式。
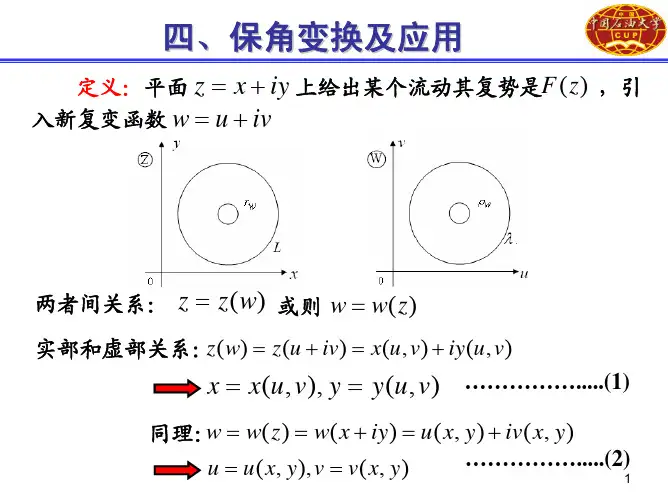
为了便于根据边界条件确定 K-M 函数,采取保角变换z = ()将物体在z 平面上所占的区域变为在平面所占的区域。
一般的说,通过保角变换可以将非圆边界映射为圆边界,使得问题得以简化。
假设将z 平面上的有限区域或者无限区域S 映射为平面的单位圆内的区域,并且将z 平面上的区域S的边界l 映射为单位圆,对应的关系如下表:由于平面上的任一点可以表示为,。
和是点的极坐标。
而根据保角变换公式z = ( ),则z平面任意一点也可以通过和表示。
因此,和又称为曲线坐标。
对于某些问题的描述中,采用曲线坐标形式表示位移和应力有利于问题的分析。
曲线坐标的概念:平面的一个圆周=const 和一条径向直线=const分别对应于z 平面的两条曲线,这两条曲线就记作=const和=const。
于是和可以看作z 平面上一点的曲线坐标。
由于变换的保角性,这个曲线坐标总是正交的,而且坐标轴和的相对位置和坐标轴Ox和Oy的相对位置相同,如图所示。
首先讨论矢量的保角变换。
设曲线坐标,即=const 与x 轴夹角,如果A 为z 平面上的任一矢量,设A 与曲线坐标夹角。
设A x, A y 分别表示矢量A 在x,y 轴的投影;A , A 表示在=const 和=const 上的投影,则上式的几何意义为,将矢量A 绕z 点顺时针方向转动角后,其在Oxy 坐标系的位置,相当于A 在曲线坐标系( , )中的位置,如图所示。