信号与系统实验题目及答案

信 号 与 系 统实 验 教 程（只有答案）（实验报告）这么玩！目录 实验一 信号与系统的时域分析 (2)三、实验内容及步骤 (2)实验二 连续时间信号的频域分析 (14)三、实验内容及步骤 (14)实验三 连续时间LTI 系统的频域分析 (35)三、实验内容及步骤 (35)实验四 通信系统仿真 (41)三、实验内容及步骤 (41)实验五 连续时间LTI 系统的复频域分析 (51)三、实验内容及步骤 (51)实验一信号与系统的时域分析三、实验内容及步骤实验前，必须首先阅读本实验原理，读懂所给出的全部范例程序。

实验开始时，先在计算机上运行这些范例程序，观察所得到的信号的波形图。

并结合范例程序应该完成的工作，进一步分析程序中各个语句的作用，从而真正理解这些程序。

实验前，一定要针对下面的实验项目做好相应的实验准备工作，包括事先编写好相应的实验程序等事项。

Q1-1：修改程序Program1_1，将dt改为0.2，再执行该程序，保存图形，看看所得图形的效果如何？dt = 0.01时的信号波形dt = 0.2时的信号波形这两幅图形有什么区别，哪一幅图形看起来与实际信号波形更像？答：Q1-2：修改程序Program1_1，并以Q1_2为文件名存盘，产生实指数信号x(t)=e-0.5t。

要求在图形中加上网格线，并使用函数axis()控制图形的时间范围在0~2秒之间。

然后执行该程序，保存所的图形。

修改Program1_1后得到的程序Q1_2如下：信号x(t)=e-0.5t的波形图clear, % Clear all variablesclose all, % Close all figure windowsdt = 0.2; % Specify the step of time variablet = -2:dt:2; % Specify the interval of timex = exp(-0.5*t); % Generate the signalplot(t,x)grid on;axis ([0 2 0 1 ])title('Sinusoidal signal x(t)')xlabel('Time t (sec)')Q1-3：修改程序Program1_1，并以Q1_3为文件名存盘，使之能够仿真从键盘上任意输入的一个连续时间信号，并利用该程序仿真信号x(t)=e-2t。

产生离散衰减正弦序列()π0.8sin 4n x n n ⎛⎫= ⎪⎝⎭, 010n ≤≤，并画出其波形图。

n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB 生成信号()0sinc at t -, a 和0t 都是实数,410t -<<，画波形图。

观察并分析a 和0t 的变化对波形的影响。

t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a 越大最大值越小，t0越大图像对称轴越往右移某频率为f 的正弦波可表示为()()cos 2πa x t ft =，对其进行等间隔抽样，得到的离散样值序列可表示为()()a t nT x n x t ==，其中T 称为抽样间隔，代表相邻样值间的时间间隔，1s f T=表示抽样频率，即单位时间内抽取样值的个数。

抽样频率取40 Hz s f =，信号频率f 分别取5Hz, 10Hz, 20Hz 和30Hz 。

请在同一张图中同时画出连续信号()a x t t 和序列()x n nT 的波形图，并观察和对比分析样值序列的变化。

可能用到的函数为plot, stem, hold on 。

fs = 40;t = 0 : 1/fs : 1 ;% ƵÂÊ·Ö±ðΪ5Hz,10Hz,20Hz,30Hz f1=5;xa = cos(2*pi*f1*t) ; subplot(1, 2, 1) ;plot(t, xa) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('t(s)') ;ylabel('Xa(t)') ;line([0, max(t)],[0,0]) ; subplot(1, 2, 2) ;stem(t, xa, '.') ;line([0, max(t)], [0, 0]) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('n') ;ylabel('X(n)') ;频率越高，图像更加密集。

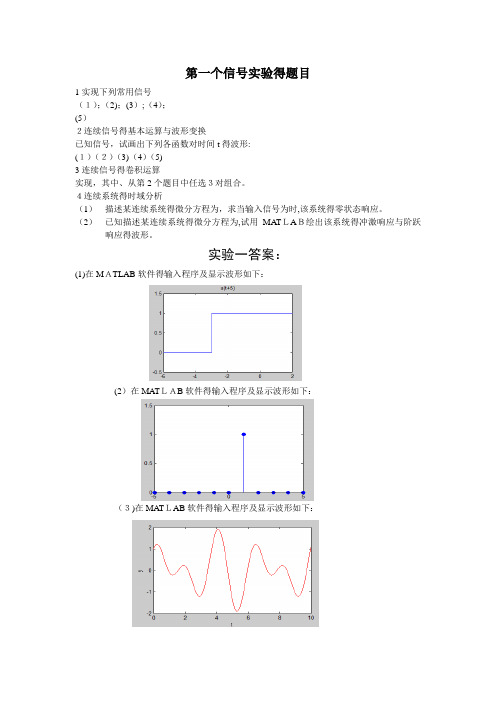
第一个信号实验得题目1实现下列常用信号（１）；（2)；(3）;（4）；(5）２连续信号得基本运算与波形变换已知信号，试画出下列各函数对时间t得波形:(１）（２）（3)（4）（5)3连续信号得卷积运算实现，其中、从第2个题目中任选３对组合。

４连续系统得时域分析（1）描述某连续系统得微分方程为，求当输入信号为时,该系统得零状态响应。

（2）已知描述某连续系统得微分方程为,试用MATＬAＢ绘出该系统得冲激响应与阶跃响应得波形。

实验一答案：(1)在MＡTLAB软件得输入程序及显示波形如下：(2）在MATＬＡB软件得输入程序及显示波形如下：（３)在MA TＬAB软件得输入程序及显示波形如下：（４)在MA TＬAB软件得输入程序及显示波形如下:（5）在ＭATLAＢ软件得输入程序及显示波形如下:（1）得输入程序及波形如下:（２）得输入程序及波形如下：(3）得输入程序及波形如下：(２)系统得冲激响应与阶跃响应如下：（4）得输入程序及波形如下：(5)得输入程序及波形如下:（1)与(2)组合得卷积运算如下：（2）与（３)组合得卷积运算如下：(1）与（3)组合得卷积运算如下：(１）系统得零状态响应如下：第二个信号实验题目1（1）用数值法求门函数得傅里叶变换，并给出门函数得幅频特性曲线与相频特性曲线.（2）用符号法给出函数得傅里叶变换。

(3)已知系统函数为，画出该系统得零极点图。

2(1）用数值法给出函数幅频特性曲线与相频特性曲线.（2)对函数进行采样，采样间隔为0、０1。

(3)已知输入信号为，载波频率为10００Ｈz,采样频率为5０0０Hz，试产生输入信号得调幅信号。

３（1）用符号法实现函数得傅里叶变换,并给出门函数得幅频特性曲线与相频特性曲线。

（2)已知系统函数为,输入信号为,求该系统得稳态响应。

（３）已知输入信号为,载波频率为100Ｈz,采样频率为400Ｈｚ,试产生输入信号得调频信号.4(1）已知系统函数为,画出该系统得零极点图.(2)已知函数用数值法给出函数得幅频特性曲线与相频特性曲线。

实验一 离散时间信号的表示及可视化一、实验目的学会对离散时间信号进行标识和可视化处理。

二、实验源程序 (1)f(n)= )(n δn=-5:1:5; f=dirac(n); plot(n,f,'.'); xlabel('(n)'); ylabel('(f)'); axis([-5 5 -0.5 1.5])(2) f(n)=ε(n)f=Heaviside(n)n=-5:1:5; f=heaviside(n); plot(n,f,'.'); xlabel('(n)'); ylabel('(f)');axis([-5 5 -0.5 1.5]) (3) f(n)= ane (分别取a>0及a<0)a=1时 n=-5:1:5; f=exp(n); plot(n,f,'.');a=-1时 n=-5:1:5; f=exp(-n); plot(n,f,'.');(4) f(n)=R N (n) (分别取不同的N 值)N=10时 n=0:1:9; f=1;plot(n,f,'.');N=15时 n=0:1:14; f=1;plot(n,f,'.') (5) f(n)=Sa(nw)w=0.1时n=-45:1:45;f=sinc(0.1*n);plot(n,f,'.');xlabel('n');ylabel('f');axis([-50 50 -1 1])w=0.2时n=-45:1:45;f=sinc(0.2*n);plot(n,f,'.');xlabel('n');ylabel('f');axis([-50 50 -1 1])(6)f(n)=Sin(nw)(分别取不同的w值)w=100时n=-15:1:15;f=sin(100*n);plot(n,f,'.');xlabel('n');ylabel('f');w=200时n=-15:1:15;f=sin(200*n);plot(n,f,'.');xlabel('n');ylabel('f');三、程序运行结果及波形图（1）（2）（3）-5-4-3-2-1012345(n)(f)-5-4-3-2-1012345(n)(f)（4）0123456789024********（5）（6）-50-40-30-20-1001020304050-1-0.8-0.6-0.4-0.200.20.40.60.81nf-50-40-30-20-1001020304050-1-0.8-0.6-0.4-0.200.20.40.60.81nffnf-15-10-5051015n四、实验调试体会实验二 连续时间信号的表示及可视化一、实验目的熟练掌握连续时间信号的表示及可视化处理。

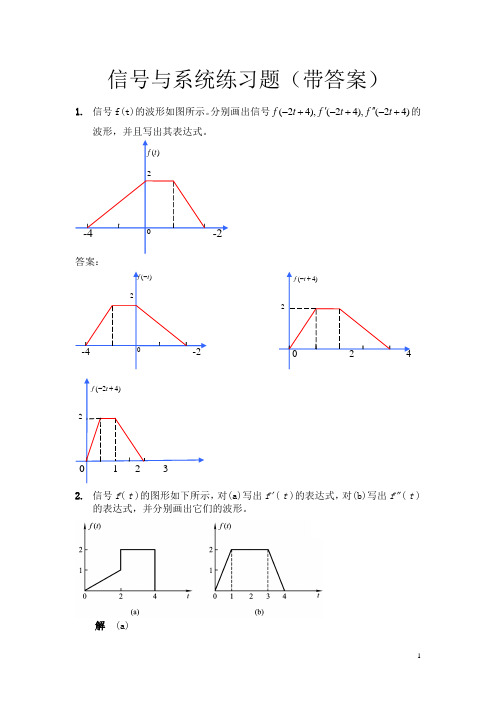
信号与系统练习题（带答案）1. 信号f(t)的波形如图所示。

分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形，并且写出其表达式。

答案：2. 信号f ( t )的图形如下所示，对(a)写出f ' ( t )的表达式，对(b)写出f " ( t )的表达式，并分别画出它们的波形。

解 (a)20,21≤≤tf ' (t)= δ(t -2)， t = 2-2δ(t -4)， t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示，试画出f(t)的波形。

52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析（）右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得－2t ，即f(5-2t)左移(52)(2)f t f t -−−−→-时移由（2）反转：f(-2t)中以-t 代替t ，可求得f(2t),表明f(-2t)的波形 以t ＝0的纵轴为中心线对褶，注意()t δ是偶数，故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由（3）尺度变换：以12t 代替f(2t)中的t ，所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。

4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。

解：{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。

信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（ ） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（ ） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（ ） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（ ） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。

2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。

3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。

实验1 信号变换与系统非时变性质的波形绘制●用MA TLAB画出习题1-8的波形。

●用MA TLAB画出习题1-10的波形。

Eg 1.8代码如下：function [y]=zdyt(t) %定义函数zdyty=-2/3*(t-3).*(heaviside(-t+3)-heaviside(-t));endt0=-10;t1=4;dt=0.02;t=t0:dt:t1;f=zdyt(t);y=zdyt(t+3);x=zdyt(2*t-2);g=zdyt(2-2*t);h=zdyt(-0.5*t-1);fe=0.5*(zdyt(t)+zdyt(-t));fo=0.5*(zdyt(t)-zdyt(-t));subplot(7,1,1),plot(t,f);title('信号波形的变化')ylabel('f(t)')grid;line([t0 t1],[0 0]);subplot(7,1,2),plot(t,y);ylabel('y(t)')grid;line([t0 t1],[0 0]);subplot(7,1,3),plot(t,x);ylabel('x(t)')grid;line([t0 t1],[0 0]);subplot(7,1,4),plot(t,g);ylabel('g(t)')grid;line([t0 t1],[0 0]);subplot(7,1,5),plot(t,h);ylabel('h(t)')grid;line([t0 t1],[0 0]);subplot(7,1,6),plot(t,fe);ylabel('fe(t)')grid;line([t0 t1],[0 0]);subplot(7,1,7),plot(t,fo);ylabel('fo(t)')grid;line([t0 t1],[0 0]);xlabel('Time(sec)')结果：Eg1.10代码如下：function [u]=f(t) %定义函数f(t) u= heaviside(t)-heaviside(t-2); endfunction [u] =y(t) %定义函数y(t)u=2*(t.*heaviside(t)-2*(t-1).*heaviside(t-1)+(t-2).*heaviside(t-2)); endt0=-2;t1=5;dt=0.01; t=t0:dt:t1; f1=f(t); y1=y(t); f2=f(t)-f(t-2); y2=y(t)-y(t-2); f3=f(t)-f(t+1); y3=y(t)-y(t+1);subplot(3,2,1),plot(t,f1); title('激励——响应波形图') ylabel('f1(t)')grid;line([t0 t1],[0 0]);-10-8-6-4-2024012信号波形的变化f (t)-10-8-6-4-2024012y (t)-10-8-6-4-2024012x (t)-10-8-6-4-2024012g (t)-10-8-6-4-2024012h (t)-10-8-6-4-202400.51f e (t)-10-8-6-4-2024-101f o (t)Time(sec)subplot(3,2,2),plot(t,y1); ylabel('y1(t)')grid;line([t0 t1],[0 0]); subplot(3,2,3),plot(t,f2); ylabel('f2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,4),plot(t,y2); ylabel('y2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,5),plot(t,f3); ylabel('f3(t)')grid;line([t0 t1],[0 0]); subplot(3,2,6),plot(t,y3); ylabel('y3(t)')grid;line([t0 t1],[0 0]); xlabel('Time(sec)')结果：实验2 微分方程的符号计算和波形绘制上机内容用MA TLAB 计算习题2-1，并画出系统响应的波形。

信号和系统试题及答案一、选择题（每题4分，共20分）1. 信号的频谱分析中，傅里叶变换的物理意义是什么？A. 信号的时域表示B. 信号的频域表示C. 信号的相位信息D. 信号的幅度信息答案：B2. 在线性时不变系统中，系统的输出与输入的关系是什么？A. 线性关系B. 非线性关系C. 时变关系D. 随机关系答案：A3. 下列哪个函数不是周期函数？A. sin(t)B. cos(2t)C. e^(-t)D. cos(2πt)答案：C4. 系统稳定性的判定可以通过什么方法？A. 奈奎斯特准则B. 伯德图C. 相位裕度D. 所有以上答案：D5. 系统函数H(s)的零点和极点分别代表什么？A. 系统输入和输出B. 系统稳定性和不稳定性C. 系统增益和衰减D. 系统频率响应答案：B二、填空题（每题4分，共20分）1. 连续时间信号的傅里叶变换定义为：X(jω) = ____________。

答案：∫x(t)e^(-jωt)dt2. 如果一个系统的冲激响应h(t)是因果的，则系统的零状态响应y(t)与输入x(t)的关系为：y(t) = ____________。

答案：∫h(t-τ)x(τ)dτ3. 一个线性时不变系统的特性可以用其系统函数H(s)来描述，其中s 是复频域变量，代表的是 ____________。

答案：拉普拉斯变换4. 如果一个系统的频率响应H(jω)在ω=ω0处有极点，则在时域中对应的响应h(t)将具有 ____________。

答案：振荡特性5. 系统的因果性意味着系统的输出不会在输入之前出现，这可以用系统的冲激响应h(t)满足的条件来表示：h(t) = ____________。

答案：0，t < 0三、简答题（每题10分，共30分）1. 请简述傅里叶级数与傅里叶变换的区别。

答案：傅里叶级数适用于周期信号，是将周期信号分解为正弦和余弦函数的和，而傅里叶变换适用于非周期信号，是将信号分解为复指数函数的积分。

信号与系统实验及参考答案1、信号的产⽣（sin,square,sinc,exp ）：利⽤matlab 函数产⽣下列信号波形：正弦波，周期⽅波，Sinc 函数，指数函数。

2、信号的运算：（1）已知x (t)=sin(t )/t ，画出x (t +3)、x (2t +3)和x (-2t +3)的波形;（2）卷积运算)],2()()[2cos()(),(5.1)(5.1)(2321??=?+=?t u t u t t x t u e t u e t x t t 其卷积积分为)(*)()(211t x t x t y =；],2[)2(]1[)1(][],1[)3/2(][2143+?=??=?+n u n u n x n u n x n n n 其卷积和为][*][][432n x n x n y =；图⽰出所有函数及卷积积分/和的波形。

3、信号的分解：将⼀个周期性连续⽅波信号分解为傅⾥叶级数（1）将⽅波分解为多次谐波之和（1，3，5…19次）。

画成如图3-1所⽰的形式。

（2）⽐较最⾼谐波次数为6次、12次和24次时的⽅波波形，如图3-2所⽰。

图3-1 图3-2电⽓信息学院2009春“信号与系统”实验1参考答案1、（图）y=sin(2*t) y=square(4*pi*t) y=sinc(t) y=exp(-t)2、（1）（参考.m⽂件及图）syms t;x=sym('sin(t)/t'); %定义符号函数x(t)=sin(t)/tx1=subs(x,t,t+3); %对x进⾏时移x2=subs(x1,t,2*t); %对x1进⾏尺度变换x3=subs(x2,t,-t); %对x2进⾏反转subplot(2,2,1);ezplot(x,[-8,8]);grid on; %ezplot是符号函数绘图命令subplot(2,2,2);ezplot(x1,[-8,8]);grid on;subplot(2,2,3);ezplot(x2,[-8,8]);grid on;subplot(2,2,4);ezplot(x3,[-8,8]);grid on;(注:也可⽤⼀条指令:subs(x,t,-2*t+3)实现到x(-2t+3)的变换)x(t) x(t+3)x(2t+3) x(-2t+3)2、（2）（参考.m ⽂件及图）cleart=linspace(-10,10,1001);x1=1.5*exp(-2*t).*stepfun(t,0);x2=cos(2*t).*(stepfun(t,0)-stepfun(t,2));x12=1.5*exp(3*t).*(stepfun(t,-10)-stepfun(t,0.0));x6=(20/1001)*conv2(x1,x2,'same');x7=(20/1001)*conv2(x2,x12,'same');subplot 231;plot(t,x1+x12);axis([-5 5 -1.5 1.5]);grid on;xlabel('{\itx}_1({\itt})')subplot 232;plot(t,x2,'k');axis([-5 5 -1.5 1.5]);grid on;xlabel('{\itx}_2({\itt})')subplot 233;plot(t,x6+x7,'r');axis([-5 5 -1.5 1.5]);grid on;xlabel('{\ity}_1({\itt})')nmin=-20;nmax=20;nleng=nmax-nmin+1;n=nmin:nmax;x3=(-2/3).^n.*stepfun(n,1);x4=(-1).^(n+1).*stepfun(n,-1)-(-2).^(n-2).*stepfun(n,2);y2=conv2(x3,x4,'same');subplot 234;stem(n,x3,'.');axis([-4 6 -1 1]);grid on;xlabel('{\itx}_3[{\itn}]')subplot 235;stem(n,x4,'.');axis([-4 6 -20 10]);grid on;xlabel('{\itx}_4[{\itn}]')subplot 236;stem(n,y2,'.');axis([-4 6 -10 7]);grid on;xlabel('{\ity}_2[{\itn}]')][3n x ][4n x ][2n y )(1t x )(2t x )(1t y3、(1) ⽅波分解为多次谐波之和clearclose allt=0:0.01:2*pi;y=zeros(10,max(size(t)));x=zeros(size(t));for k=1:2:19 x=x+sin(k*t)/k;y((k+1)/2,:)=x;endsubplot(211),plot(t,y(1:9,:)),grid on;line([0,pi+0.5],[pi/4,pi]); text(pi+0.5,pi/4,'pi/4'); axis([0,2*pi,-1,1])halft=ceil(length(t)/2);subplot(212),mesh(t(1:halft),[1:10],y(:,1:halft))3、(2)⽅波的傅⾥叶级数,最⾼谐波次数为6, 12和34的波形⽐较tau_T=3/4; % 占空⽐3/4n_max=[6 12 34]; % 最⾼谐波次数:6,12,34 N=length(n_max); % 计算N次t=-1.1:.002:1.1;omega_0=2*pi; % 基波频率for k=1:Nn=[];n=[-n_max(k):n_max(k)];L_n=length(n);F_n=zeros(1,L_n);for i=1:L_n % 计算傅⾥叶复系数Fn F_n(i)=tau_T*sinc(tau_T*n(i))*exp(-j*tau_T*n(i)*pi);endF=F_n*exp(j*omega_0*n'*t); % 计算前⼏项的部分和subplot(N,1,k),plot(t,real(F),'linewidth',2); % 在N幅图中的第k⼦图画实部波形 axis([-1.1 1.1 -0.5 1.5]);line([-1.1 1.1],[0 0],'color','r'); % 画直线,表⽰横轴,线为红⾊ line([0 0],[-0.5 1.5],'color','r'); % 画直线,表⽰纵轴,线为红⾊bt=strcat('最⾼谐波次数=',num2str(n_max(k))); % 字符串连接title(bt); % 在N幅图中的第k⼦图上写标题end。