广东省中山市普通高中高考数学一轮复习模拟试题02

广东省中山市2024高三冲刺（高考数学）统编版（五四制）真题(预测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题若1，a，3成等差数列，1，b，4成等比数列，则的值为（）A．B．C．1D．第(2)题正方体中，点在棱上，过点作平面的平行平面，记平面与平面的交线为，则与所成角的大小为（）A．B．C．D．第(3)题已知点，动点在圆上，则的最小值为（）A．B．C．D．第(4)题已知函数,则的值域是（）A．B．C．D．第(5)题《周髀算经》中给出的弦图是由四个全等的直角三角形和中间一个小正方形拼成的一个大的正方形，若下图中所示的角为（），且小正方形与大正方形面积之比为，则的值为（）A．B．C．D．第(6)题若函数在上单调递增，则实数的取值范围是（）A．B．C．D．第(7)题已知定义在上的函数满足，当时，.设在上的最大值为，且的前项和为，则（）A．3B．C．2D．第(8)题已知向量，，，若，则（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题盒子中共有2个白球和3个黑球，从中不放回任取两次，每次取一个，则下列说法正确的是（）A．“取到2个白球”和“取到2个黑球”是对立事件B．“第一次取到白球”和“第二次取到黑球”是相互独立事件C．“在第一次取到白球的条件下，第二次取到黑球”的概率为D．设随机变量和分别表示取到白球和黑球的个数，则第(2)题已知函数，则（）A．是偶函数B ．在区间上单调递增C ．在上有4个零点D ．的值域是第(3)题下列化简正确的是（ ）A ．B ．C．D ．三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题设定义在上且，则______．第(2)题已知椭圆C ：的左，右焦点分别是是椭圆C 上第一象限内的一点，且的周长为.过点作的切线，分别与轴和轴交于两点，为原点，当点在上移动时，面积的最小值为___________.第(3)题已知函数，若这两个函数的图象在公共点处有相同的切线，则_________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题如图，在四棱锥中，平面平面BCDE ，，，为等边三角形，．(1)求证：平面ACD ．(2)已知，，求平面ADE 与平面ABE 所成锐二面角的余弦值．第(2)题已知数列是公差为2的等差数列，其前3项的和为12，是公比大于0的等比数列，，.(1)求数列和的通项公式；(2)若数列满足，求的前项和.第(3)题已知数列的通项公式为，其中，、.(1)试写出一组、的值，使得数列中的各项均为正数.(2)若，，数列满足，且对任意的()，均有，写出所有满足条件的的值. (3)若，数列满足，其前项和为，且使(、，)的和有且仅有组，、、…、中有至少个连续项的值相等，其它项的值均不相等，求、的最小值.第(4)题已知的内角，，所对的边分别为，，，，．(1)求；(2)若为上一点，，，求的面积．第(5)题已知抛物线C ：的焦点为F ，A 是C 上一点且位于第一象限，直线与C 交于另一点B ，直线（O 为坐标原点）与直线交于点D ，且与x 轴平行．(1)求抛物线C 的方程．(2)若，点P ，Q 是C 上与A 不重合的动点，直线与的斜率之积为，判断直线是否过定点？若过定点，写出定点坐标；若不过定点，请说明理由．。

广东省中山市（新版）2024高考数学统编版（五四制）真题(综合卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是A．B ．C ．D ．第(2)题记为等差数列的前n 项和．已知，则A ．B ．C ．D ．第(3)题已知直线交曲线于，两点（点在点的上方），为的焦点，则（ ）A ．B ．C．2D ．第(4)题已知集合，，则（ ）A ．B ．C ．D ．第(5)题吉林雾淞大桥，位于吉林市松花江上，连接雾淞高架桥，西起松江东路，东至滨江东路．雾淞大桥是吉林市第一座自锚式混凝土悬索桥，两主塔左、右两边悬索的形状均为抛物线（设该抛物线的焦点到准线的距离为米）的一部分，左：右两边的悬索各连接着29根吊索，且同一边的相邻两根吊索之间的距离均为米（将每根吊索视为线段）．已知最中间的吊索的长度（即图中点到桥面的距离）为米，则最靠近前主塔的吊索的长度（即图中点到桥面的距离）为（ ）A ．米B ．米C ．米D ．米第(6)题抛物线的准线方程是（ ）A．B ．C．D ．第(7)题在中，若，，则（ ）A．B ．C ．D ．第(8)题若，则（ ）A ．55B ．56C ．45D ．46二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题抛物线的焦点为，准线为直线，过点的直线交抛物线于，两点，分别过，作抛物线的切线交于点，于点，于点，则（ ）A ．点在直线上B ．点在直线上的投影是定点C．以为直径的圆与直线相切D．的最小值为第(2)题若函数对定义域D内的每一个，都存在唯一的，使得成立，则称为“自倒函数”．则下列结论正确的是（）A．f(x)＝sin x+（x∈[－，]）是“自倒函数”B．“自倒函数”可以是奇函数C．“自倒函数”的值域可以是RD．若都是“自倒函数”且定义域相同，则也是“自倒函数”第(3)题已知，则（）A．的最大值为B．的最小值为C．的最大值为2D．的最小值为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题若奇函数，则__________．第(2)题已知,则________．（用数字作答）第(3)题已知函数在上的最小值为1，则的值为________.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知．（1）已知函数h（x）=g（x）+ax3的一个极值点为1，求的取值；（2）求函数在上的最小值；（3）对一切，恒成立，求实数a的取值范围．第(2)题在中，，D为中点.(1)若，求；(2)若，求的值.第(3)题一批大学生和公务员为了响应我党提出的“精准扶贫”政策，申请报名参加新疆某贫困地区开展脱贫工作的“进村工作”活动，帮助当地农民脱贫致富.该区有四个村，政府组织了四个扶贫小组分别进驻各村，开展“进村工作”，签约期两年.约期完后，统计出该区四村的贫富情况条形图如下：(1)若该区脱贫率为80％，根据条形图，求出村的总户数；(2)约期完后，政府打算从四个小组中选出两个小组颁发金星级奖与银星级奖，每个小组被选中的可能性相同.求进驻村的工作小组被选中的概率.第(4)题在平面直角坐标系中，直线的参数方程为（为参数），曲线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系．(1)求与的极坐标方程；(2)若与的两不同交点满足，求的值．第(5)题已知函数.(1)若在定义域内无极值点，求实数的取值范围；(2)求证：当时，恒成立.。

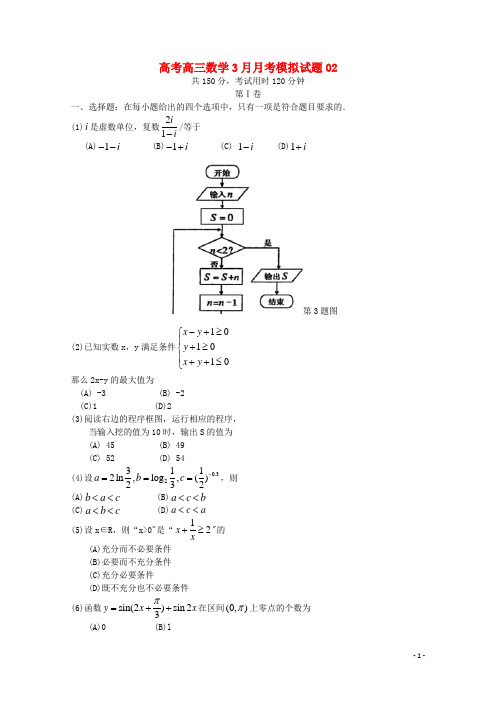
高考高三数学3月月考模拟试题02共150分，考试用时120分钟第Ⅰ卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．(1)i 是虚数单位，复数21ii-/等于 (A)1i -- (B)1i -+ (C) 1i - (D)1i +第3题图(2)已知实数x ，y 满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩那么2x-y 的最大值为(A) -3 (B) -2 (C)1 (D)2(3)阅读右边的程序框图，运行相应的程序， 当输入挖的值为10时，输出S 的值为 (A) 45 (B) 49 (C) 52 (D) 54(4)设0.323112ln,log ,()232a b c -===，则 (A)b a c << (B)a c b << (C)a b c << (D)a c a <<(5)设x ∈R ，则“x>0"是“12x x+≥"的(A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件(D)既不充分也不必要条件 (6)函数sin(2)sin 23y x x π=++在区间(0,)π上零点的个数为(A)0 (B)l(C)2 (D)3(7)直角三角形ABC 中，90,2,1C AB AC ∠===，点D 在斜边AB 上，且AD AB λ=,R λ∈,若2CD CB ⋅=，则λ=(A)12(B)13）23(8)下列函数中，同时具有性质：①图象过点(0，1):②在区间(0,)+∞上是减函数； ③是偶函数。

这样的函数是(A)1()()2xf x = (B)()lg(2)f x x =+ (C)12()f x x = (D)()2xf x =第Ⅱ卷二、填空题：本大题共6小题，每小题5分，共30分． (9)已知集合{}|12,A x x =->{}|(5)0B x x x =-<, 则AB =________．11图(10)一个几何体的三视图如图所示（单位：m ）， 则该几何体的体积为_______2m ． (11)如图，ABC ∆内接于圆O ，过点C 的切线交 AB 的延长线于点D ，若10,6,9AB BC AC ===， 则切线DC 的长为____．(12)若(,)a b c c在圆221x y +=上，则直线0ax by c ++=与圆222x y +=相交所得弦的长为_____________。

解析几何专题二：圆锥曲线弦长问题一、知识储备弦长公式||AB =12||AB x ==-= （最常用公式，使用频率最高）= 二、例题讲解1．（2022·辽宁高三开学考试）已知椭圆C 的标准方程为：22221(0)x y a b a b +=>>，若右焦点为F（1）求椭圆C 的方程；（2）设M ，N 是C 上的两点，直线MN 与曲线222x y b +=相切且M ，N ，F 三点共线，求线段MN 的长． 【答案】（1）2213x y +=；（2【分析】（1）根据椭圆的焦点、离心率求椭圆参数，写出椭圆方程即可.（2）由（1）知曲线为221(0)x y x +=>，讨论直线MN 的存在性，设直线方程联立椭圆方程并应用韦达定理求弦长即可. 【详解】（1）由题意，椭圆半焦距c =c e a =，则a =2221b a c =-=， ∴椭圆方程为2213x y +=；（2）由（1）得，曲线为221(0)x y x +=>当直线MN 的斜率不存在时，直线:1MN x =，不合题意：当直线MN 的斜率存在时，设()11,M x y ，()22,N x y 又M ，N ，F 三点共线，可设直线:(MN y k x =，即0kx y -=， 由直线MN 与曲线221(0)x y x +=>1=，解得1k =±，联立22(13y x x y ⎧=±⎪⎨+=⎪⎩，得2430x -+=，则12x x +=1234x x ⋅=，∴||MN ==2．（2022·全国高三专题练习）过双曲线142x y -=的右焦点F 作斜率为2的直线l ，交双曲线于A ，B 两点.（1）求双曲线的离心率和渐近线； （2）求AB 的长. 【答案】（1）e =，渐近线方程为y =；（2）207.【分析】（1）由双曲线方程得出,a b ，再求出c ，可得离心率，渐近线方程；（2）写出直线方程，代入双曲线方程，设()11,A xy ，()22,B x y，由韦达定理得1212,x x x x +，然后由弦长公式计算弦长． 【详解】解：（1）因为双曲线方程为22142x y -=， 所以2a =，b =则c =所以62cea，渐近线方程为2y x =±. （2）双曲线右焦点为0)，则直线l 的方程为2(y x = 代入双曲线22142x y -=中，化简可得27520x -+=设()11,A x y ，()22,B x y 所以12x x +=12527x x ⋅=，所以2120|||7AB x x -==. 【点睛】方法点睛：本题考查双曲线的离心率和渐近线方程，考查直线与双曲线相交弦长．解题方法是直线方程与双曲线方程联立并消元后应用韦达定理求出1212,x x x x +，然后由弦长公式12d x =-求出弦长．3．（2022·全国高三模拟预测）在平面直角坐标系xOy 中，已知()2,0F ，()2,3M -，动点P 满足12OF MP PF ⋅=． （1）求动点P 的轨迹C 的方程；（2）过点()1,0D 作直线AB 交C 于A ，B 两点，若AFD 的面积是BFD △的面积的2倍，求AB ． 【答案】（1）28y x =；（2【分析】（1）设(),P x y ，求得,,MP OF PF 的坐标，结合12OF MP PF ⋅=，化简、整理，即可求得抛物线的方程； （2）设()()1122,,,A x y B x y ，不妨设120,0y y ><，由2AFD BFD S S =△△，求得122y y =-，设直线AB 的方程为1x my =+，联立方程组，结合根与系数的关系，求得128y y m +=，128y y =-，进而求得12,,y y m ，利用弦长公式，即可求解. 【详解】（1）设(),P x y ，因为()2,0F ，()2,3M -，则()2,3MP x y =+-，()2,0OF =，()2,PF x y =--． 由12OF MP PF ⋅=，可得2x +=28y x =，即动点P 的轨迹C 的方程为28y x =． （2）设()11,A x y ，()22,B x y ， 由题意知112AFD S FD y =⋅△，212BFD S FD y =⋅△， 易知120y y <，不妨设120,0y y ><，因为2AFD BFD S S =△△，所以122y y =，所以122y y =-． ① 设直线AB 的方程为1x my =+，联立281y xx my ⎧=⎨=+⎩消去x ，得2880y my --=，则264320m ∆=+>，可得128y y m +=，128y y =- ② 由①②联立，解得1214,2,4y y m ==-=，所以124(2)AB y =-=--=． 【点睛】本题主要考查了向量的坐标运算，抛物线的标准方程的求解，以及直线与抛物线的位置关系的综合应用,解答此类题目，通常联立直线方程与抛物线方程，应用一元二次方程根与系数的关系进行求解，此类问题易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等．三、实战练习1．（2022·江门市培英高级中学高三模拟预测）已知椭圆()2222:10x y C a b a b +=>>过点P ⎭，离心率为12． （1）求椭圆C 的标准方程；（2）若1A 为椭圆C 的左顶点，直线l 过右焦点2F 与椭圆C 交于M ，N 两点（M ，N 与1A 不重合），l 不与x 轴垂直，若11A M A N MN k k k +=-，求MN ．【答案】（1）22143x y +=；（2）247 【分析】（1）由题意可得关于,,a b c 的方程组，求解,a b 的值，即可求得椭圆C 的标准方程；（2）根据题意设()()1122,,,M x y N x y ，直线l ：()1,0x my m =+≠，联立直线方程与椭圆方程，化为关于y 的一元二次方程，利用根与系数的关系结合11A M A N MN k k k +=-，求出m 的值，再根据弦长公式即可求得MN . 【详解】（1）由题意可得：22222123314c a a b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得：224,3a b ==，∴ 椭圆C 的标准方程为：22143x y +=； （2）()()211,0,2,0F A -，由题意可设：直线l ：()1,0x my m =+≠，()()1122,,,M x y N x y ，联立：221143x my x y =+⎧⎪⎨+=⎪⎩ 得：()2234690m y my ++-=， 则12122269,3434m y y y y m m --+==++， 1112121,,22A M A N MN y y k k k x x m===++， 11121222A M A N y yx k x k ∴+=+++ ()()()()1221122222y x y x x x +++=++()()()()1221213333y my y my my my +++=++()()2122112122339y y y m y y y my m y ++=+++222229623343496393434mm m m m m m m m --⨯+⨯++=--⨯+⨯+++ m =-，又11A M A N MN k k k +=-， 1m m∴-=-， 解得：21,1m m ==±， 故1212226699,347347m y y y y m m --+==±==-++，247MN =.2．（2022·广东执信中学高三月考）已知椭圆C 的方程为22221(0)x y a b a b +=>>，右焦点为F．（1）求椭圆C 的方程；（2）设M ，N 是椭圆C 上的两点，直线MN 与曲线222(0)x y b x +=>相切．证明：M ，N ，F三点共线的充要条件是||MN =【答案】（1）2213x y +=；（2）证明见解析.【分析】（1）由离心率公式可得a =2b ，即可得解；（2）必要性：由三点共线及直线与圆相切可得直线方程，联立直线与椭圆方程可证MN =充分性：设直线():,0MN y kx b kb =+<，由直线与圆相切得221b k=+，联立直线与椭圆方程结合弦长公式可得=1k =±，即可得解. 【详解】（1）由题意，椭圆半焦距c =c e a =，所以a = 又2221b a c =-=，所以椭圆方程为2213x y +=；（2）由（1）得，曲线为221(0)x y x +=>，当直线MN 的斜率不存在时，直线:1MN x =，不合题意； 当直线MN 的斜率存在时，设()()1122,,,M x y N x y ， 必要性：若M ，N，F 三点共线，可设直线(:MN y k x =即0kx y --=，由直线MN 与曲线221(0)x y x +=>1=，解得1k =±，联立(2213y x x y ⎧=±⎪⎨⎪+=⎩可得2430x -+=，所以121234x x x x +⋅=，所以MN ==所以必要性成立；充分性：设直线():,0MN y kx b kb =+<即0kx y b -+=， 由直线MN 与曲线221(0)x y x +=>1=，所以221b k =+，联立2213y kx b x y =+⎧⎪⎨+=⎪⎩可得()222136330k x kbx b +++-=， 所以2121222633,1313kb b x x x x k k -+=-⋅=++，所以MN === 化简得()22310k -=，所以1k =±，所以1k b =⎧⎪⎨=⎪⎩1k b =-⎧⎪⎨=⎪⎩:MN y x =或y x =-+所以直线MN 过点F ，M ，N ，F 三点共线，充分性成立； 所以M ，N ，F 三点共线的充要条件是||MN = 【点睛】 关键点点睛：解决本题的关键是直线方程与椭圆方程联立及韦达定理的应用，注意运算的准确性是解题的重中之重.3．（2022·全国高三月考（文））已知椭圆2222:1(0)x y C a b a b+=>>与抛物线24y x =有公共的焦点F ，1A ，2A 分别为椭圆C 长轴的左、右端点，P 为C 上一动点，且12PAA ∆的最大面积为 （1）求椭圆C 的标准方程；（2）直线l 经过点F ，且与C 交于A ，B 两点，若10||3AB =，求直线l 的方程． 【答案】（1）22143x y +=；（20=． 【分析】（1）利用已知条件可以直接得出焦点F 的坐标，当三角形面积最大时P 为短轴端点，从而解出a ，b 的值即可； （2）利用（1）中求出的点F 的坐标，设出直线方程，然后与椭圆方程联立，利用弦长公式即可求出直线的方程． 【详解】（1）抛物线24y x =的焦点F 坐标为()1,0∴椭圆C 中的半焦距为1．由椭圆的几何性质可知，当12PA A ∆面积最大时，P 为椭圆短轴端点，不妨令()0,P b ，则221a b ab ⎧-=⎪⎨=⎪⎩解得2a b =⎧⎪⎨=⎪⎩∴椭圆C 的标准方程为22143x y +=． （2）直线l 经过椭圆C 的右焦点，且10||3AB =∴直线l 的斜率存在，设直线l 的斜率为k ，则直线l 的方程为(1)y k x =-， 与椭圆C 的方程联立可得()22223484120k xk x k +-+-=，0∆>，设()11,A x y ，()22,B x y ，则2122834k x x k +=+，212241234k x x k -=+12||AB x ∴-=()2212110343k k +==+解得k =∴直线l 0=0．【点睛】本题考查椭圆的标准方程、抛物线的几何性质以及直线与椭圆的位置关系，要求较高的运算求解能力，属于中档题.本题的关键点有：（1）韦达定理的应用，韦达定理是联系各个变量之间的桥梁是解决解析几何问题的重要方法； （2）计算能力和计算技巧是解决解析几何问题的关键能力.4．（2022·陕西（文））已知点B 是圆22:(1)16C x y -+=上的任意一点，点(1,0)F -，线段BF 的垂直平分线交BC 于点P .（1）求动点P 的轨迹E 的方程；（2）直线:2l y x m =+与E 交于点M ，N ，且MN =m 的值. 【答案】（1）22143x y +=，（2）1m =±.（1）由条件可得42PC PF PC PB BC FC +=+==>=，然后由椭圆的定义可求出答案；（2）设()()1122,,,M x y N x y ，然后联立直线与椭圆的方程消元，韦达定理得出1212,x x x x +，然后利用MN =出m 的值即可. 【详解】（1）由条件可得42PC PF PC PB BC FC +=+==>=所以动点P 的轨迹E 是以,F C 为焦点的椭圆，设其方程为()222210x y a b a b+=>>所以24,22a c ==，所以2,1,a c b ===所以方程为22143x y += （2）设()()1122,,,M x y N x y联立221432x y y x m ⎧+=⎪⎨⎪=+⎩可得221916+4120x mx m +-= 所以由()22256764120m m ∆=-->得(m ∈2121216412,1919m m x x x x -+=-=因为MN =所以可解得1m =±5．（2022·全国高三专题练习）已知点(A 和B ，动点C到A ，B 两点的距离之差的绝对值为2，记点C 的（1）求轨迹E 的方程；（2）设E 与直线2y x =-交于两点M ，N ，求线段MN 的长度. 【答案】（1）2212y x -=；（2）【分析】（1）设(,)C x y ，由于||||2CA CB -=，||AB =，利用双曲线的定义求解即可； （2）直线和双曲线方程联立消y ，利用韦达定理以及弦长公式求解即可. 【详解】 （1）设(,)C x y ， 则||||2CA CB -=，所以点C 的轨迹E 为双曲线22221(0,0)x y a b a b-=>>，且22a =，2||c AB == 则1a =，2222b c a =-=， 所以轨迹E 的方程为2212y x -=；（2）由22122y x y x ⎧-=⎪⎨⎪=-⎩， 得2460x x +-=， 因为0∆>，所以直线与双曲线有两个交点， 设()11,M x y ，()22,N x y ， 则124x x +=-，126x x =-，故MN =所以线段MN 的长度为6．（2022·全国高三专题练习）已知双曲线C ：22221(0,0)x y a b a b-=>>)是双曲线的一个顶点．（1）求双曲线的方程；（2）经过双曲线右焦点2F 作倾斜角为30的直线，直线与双曲线交于不同的两点A ，B ，求AB ． 【答案】（1）22136x y -=；（2【分析】（1)求出,a b ，即可得出双曲线方程；（2）可先求出直线方程为3)y x =-，联立椭圆方程，再利用弦长公式即可求出. 【详解】（1）由题可得c a a ⎧=⎪⎨⎪=⎩3c =，b ，所以双曲线的方程为22136x y-=；（2）双曲线22136x y -=的右焦点为()23,0F所以经过双曲线右焦点2F 且倾斜角为30°的直线的方程为3)y x =-.联立221363)x y y x ⎧-=⎪⎪⎨⎪-⎪⎩得256270x x +-=．设()11,A x y ，()22,B x y ，则1265x x +=-，12275x x =-．所以AB ==【点睛】本题考查双曲线方程的求法，考查直线与双曲线相交弦长的求法，属于基础题.7．（2022·重庆高三模拟预测）已知直线l ：4y kx =+与抛物线C ：2y ax =交于A 、B 两点，O 为坐标原点，OA OB ⊥． （1）求抛物线C 的标准方程；（2）若过点A 的另一条直线1l 与抛物线C 交于另一点M ，与y 轴交于点N ，且满足||||AN AM =，求BM 的最小值．【答案】（1）214y x =；（2）【分析】（1）先联立直线与抛物线，得到判别式和韦达定理，再根据垂直关系，利用0OA OB ⋅=，求得参数即可；（2）设直线BM 的方程，并与抛物线联立，得到判别式和韦达定理，根据已知关系，判断中点位置，利用坐标关系求得参数m ，最后利用弦长公式计算BM ，利用二次函数判断最小值即可. 【详解】解：（1）依题意，设()()1122,,,A x y B x y ，由24y ax y kx ⎧=⎨=+⎩，消去y ，得240ax kx --=，2121604k a x x a ⎧∆=+>⎪∴⎨=-⎪⎩， OA OB ⊥，12120OA OB x x y y ∴⋅=+=，即2212120x x ax ax +⋅=，即22212120x x a x x +=，所以22440a a a ⎛⎫⎛⎫-+⋅-= ⎪ ⎪⎝⎭⎝⎭，解得14a =，∴抛物线C 的标准方程为214y x =； （2）由题意知，直线BM 的斜率存在，故可设直线BM 的方程为y tx m =+，()33,M x y ，由214y xy tx m ⎧=⎪⎨⎪=+⎩，消去y ，得2440x tx m --=，223231616044t m x x m x x t ⎧∆=+>⎪∴=-⎨⎪+=⎩，由（1）知，1216x x =-，故1123321644x x x x x x m m-===-， 由题意知,,A M N 三点共线，且|AN |＝|AM |，即A 为线段MN 的中点，设()0,N n ， 则3102x x +=，即13142x x m ==，即8m =，22323161680324t x x x x t⎧∆=+⨯>⎪∴=-⎨⎪+=⎩，23BM x ∴=-=)20t ==≥， 故20t =时，BM最小为=【点睛】 思路点睛：直线与抛物线中的弦长问题，我们常让直线与抛物线方程联立，再利用韦达定理及弦长公式，建立关系式．其中弦长公式：（已知直线上的两点距离）设直线:l y kx m =+，l 上两点()()1122,,,A x y B xy ，所以12AB x =-或12AB y =-，解决相关问题.8．（2022·全国高三模拟预测）已知抛物线()2:20C y px p =>的焦点为F ，点(),2P t -在C 上，且2PF OF =(O 为坐标原点).（1）求C 的方程；（2）若A ，B 是C 上的两个动点，且A ，B 两点的横坐标之和为8，求当AB 取最大值时，直线AB 的方程. 【答案】（1）24yx =；（2）220x ±-=. 【分析】（1）根据题意，列出方程组22242pp t pt⎧+=⨯⎪⎨⎪=⎩，求得p 的值，即可求得C 的标准方程； （2）设()11,A x y ，()22,B x y ，当12x x =时，得到AB 的方程4x =；当12x x ≠时，得到2AB k n =，得到()42nx y n =-+，联立方程组，结合根与系数的关系，得到1212,y y y y +，根据弦长公式和基本不等式，即可求解. 【详解】（1）由题意，点(),2P t -在()2:20C y px p =>上，且2PF OF =，可得22242pp t pt ⎧+=⨯⎪⎨⎪=⎩，解得21p t =⎧⎨=⎩，所以C 的标准方程为24y x =.（2）设()11,A x y ，()22,B x y ，且128x x +=，设AB 中点为(),D m n ，则122x x m +=，122y y n +=， 当12x x =时，:4AB l x =，8AB =； 当12x x ≠时，()212122212121442AB y y y y k x x y y y y n--====--+， 则()2:4AB l y n x n-=-，即()42n x y n =-+，与C 联立方程消去x ，整理得2222160y ny n -+-=， 由22(2)4(216)0n n ∆=--->，解得216n <，且122y y n +=，212216y y n =-，所以2212416102n n AB y ++-=-==， 当26n =时取“=”，所以AB 的最大值为10，此时AB 的方程为220x -=. 【点睛】直线与圆锥曲线的综合问题的求解策略：对于直线与圆锥曲线的位置关系的综合应用问题，通常联立直线方程与圆锥曲线方程，应用一元二次方程根与系数的关系，以及弦长公式等进行求解，此类问题易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、运算求解能力．9．（2022·浙江高三模拟预测）已知直线:4l y kx =+与抛物线2:C y ax =交于A 、B 两点，O 为坐标原点，OA OB ⊥. （1）求抛物线C 的标准方程；（2）若过点A 的另一条直线1l 与抛物线C 交于另一点M ，与y 轴交于点N ，且满足AN AM =，求BM 的最小值. 【答案】（1）24x y=；（2）最小值为【分析】（1）联立直线l 与抛物线C 的方程，列出韦达定理，由已知条件可得出0OA OB ⋅=，利用平面向量数量积的坐标运算结合韦达定理求出a 的值，即可得出抛物线C 的标准方程；（2）设直线BM 的方程为y tx m =+，点()33,M x y ，将直线BM 的方程与抛物线C 的方程联立，列出韦达定理，由已知条件可得1312x x =，代入韦达定理求出m 的值，再利用弦长公式可求得BM 的最小值.【详解】（1）依题意设()11,A x y 、()22,B x y ，由24y ax y kx ⎧=⎨=+⎩消去y ，得240ax kx --=，所以，212160,4.k a x x a ⎧+>⎪⎨=-⎪⎩OA OB ⊥，12120OA OB x x y y ∴⋅=+=，即22212120x x a x x +=，4160a∴-+=，解得14a =，所以，抛物线C 的标准方程为24x y =；（2）由题意知，若直线BM 的斜率不存在，则该直线与抛物线C 只有一个公共点，不合乎题意.所以，直线BM 的斜率存在，故可设直线BM 的方程为y tx m =+，点()33,M x y ， 由24x y y tx m ⎧=⎨=+⎩消去y ，得2440x tx m --=，223231616044t m x x t x x m⎧+>⎪∴+=⎨⎪=-⎩， 由（1）知1216x x =-，1123231644x x x x x x m m-∴===-①. 由题意知A 、M 、N 三点共线，且A 为线段MN 的中点，设()0,N n ，则3102x x +=，即1312x x =②，由①②得8m =，22323161680432t x x t x x ⎧+⨯>⎪∴+=⎨⎪=-⎩，23BM x ∴=-=)20t ==≥，当且仅当0t =时，等号成立，故BM 的最小值为【点睛】方法点睛：圆锥曲线中的最值问题解决方法一般分两种：一是几何法，特别是用圆锥曲线的定义和平面几何的有关结论来求最值；二是代数法，常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题，然后利用基本不等式、函数的单调性或三角函数的有界性等求最值．10．（2022·全国高三专题练习）如图所示，A ，B 是焦点为F 的抛物线24y x =上的两动点，线段AB 的中点M 在定直线34x =上.（1）求FA FB +的值； （2）求AB 的最大值. 【答案】（1）72；（2）【分析】（1）由抛物线定义有12FA FB x x p +=++，结合已知条件即可求FA FB +；（2）由直线与抛物线位置关系，联立方程得到一元二次方程，结合根与系数关系、弦长公式即可求AB 的最大值. 【详解】（1）由题意知：2p =，抛物线对称轴方程1x =-.设()11,A x y ，()22,B x y ，12324x x +=，则1272FA FB x x p +=++=； （2）点A 和B 在抛物线24y x =上，有2114y x =，2224y x =，两式相减得：()()()1212124y y y y x x -+=-，令3(,)4M m ，∴12122y y x x m -=-，即2AB k m=， ∴设直线AB 的方程为234y m x m ⎛⎫-=- ⎪⎝⎭，即23224m m x y =-+，代入抛物线方程得222230y my m -+-=，∴22248121240m m m ∆=-+=->，得203m ≤<，122y y m +=，21223y y m =-∴12AB y =-=∴当20m=时，max AB = 【点睛】思路点睛：求抛物线焦半径相关线段长度时注意抛物线定义的应用，即抛物线焦点到抛物线上点的距离等于该点到抛物线准线的距离；直线与抛物线相交，求弦长时一般要联立方程应用根与系数关系以及弦长公式.11．（2022·全国高三专题练习）已知抛物线C ：22(0)y px p =>的焦点F 与椭圆22143x y +=的右焦点重合，点M 是抛物线C 的准线上任意一点，直线MA ，MB 分别与抛物线C 相切于点A ，B .（1）求抛物线C 的标准方程；（2）设直线MA ，MB 的斜率分别为1k ，2k ，证明：12k k ⋅为定值； （3）求AB 的最小值.【答案】（1）24y x =；（2）证明见解析；（3）4.【分析】（1）由椭圆的方程可得右焦点的坐标，由题意可得抛物线的焦点坐标，进而可得抛物线的方程；（2）可设M 的坐标，设过点(1,)M t -的直线方程为(1)y k x t =++，与抛物线方程24y x =联立，消去x 得：24440ky y k t -++=，利用判别式等于零可得结论；（3）设A ，B 的坐标，由（2）可得参数t ，k 的关系，代入过M 的切线方程与抛物线的方程中，可得A ，B 用参数1k ，2k 表示的坐标，代入弦长公式中求||AB的表达式，由参数的范围求出||AB 的最小值．【详解】（1）由椭圆方程得，椭圆的右焦点为(1,0) ∴抛物线的焦点为(1,0)F ，2p ∴=，所以抛物线的标准方程：24y x =． （2）抛物线C 的准线方程为1x =-． 设(1,)M t -，设过点(1,)M t -的直线方程为(1)y k x t =++，与抛物线方程24y x =联立，消去x 得：24440ky y k t -++=． 其判别式△1616()k k t =-+，令△0=，得：210k kt +-=． 由韦达定理知12k k t +=-，121k k =-， 故121k k =-（定值）．（3）设1(A x ，1)y ，2(B x ，2)y ，由210k kt +-=，得21k t k-=，故2222214244444440k ky y k t ky y k ky y k y k k k -⎛⎫-++=-++⨯=-+=-= ⎪⎝⎭，所以2y k=，代入抛物线方程得21x k =，所以211(A k ，12)k ，221(B k ，22)k ，||AB=因为121k k =-，12k k t +=-，所以12|||AB k k -244t =+，当且仅当0t =时取等号． 当且仅时取等号． 故||AB 的最小值为4．【点睛】求曲线弦长的方法：（1）利用弦长公式12l x -；（2）利用12l y =-；（3）如果交点坐标可以求出，利用两点间距离公式求解即可.12．（2022·广西河池·高三期末（理））已知抛物线2:4C y x =的焦点为F ，斜率为2的直线l 与抛物线C 相交于A 、B 两点．（Ⅰ）若直线l 与抛物线C 的准线相交于点P ，且PF =l 的方程； （Ⅱ）若直线l 不过原点，且90AFB ∠=︒，求ABF 的周长．【答案】（Ⅰ）2y x =；（Ⅱ）15+【分析】（Ⅰ）设直线l 的方程为2y x m =+，则点P 的坐标为()1,2m --，联立直线与抛物线，由判别式大于0可得12m <，由PF =0m =或4m =（舍去），从而可得结果；（Ⅱ）设直线l 的方程为()20=+≠y x b b ，并代入抛物线2:4C y x =，根据韦达定理和0FA FB ⋅=可解得12b =-，根据弦长公式可得||AB =||||AF BF +，进一步可得ABF 的周长. 【详解】（Ⅰ）由抛物线2:4C y x =可知(1,0)F ，准线为1x =-， 设直线l 的方程为2y x m =+，则点P 的坐标为()1,2m --，联立方程242y x y x m⎧=⎨=+⎩，消去y 后整理为()224440x m x m +-+=，又由()22441616320m m m ∆=--=->，可得12m <，由点F 的坐标为()1,0，有PF ==， 解得0m =或4m =（舍去）， 故直线l 的方程为2y x =．（Ⅱ）设直线l 的方程为()20=+≠y x b b ， 点A 、B 的坐标分别为()11,x y ，()22,x y ，联立方程242y x y x b⎧=⎨=+⎩，消去y 后整理为()224440x b x b +-+=，可得121x x b +=-，21214x x b =，()()()()222121212122242212y y x b x b x x b x x b b b b b b =++=+++=+-+=又由()22441616320b b b ∆=--=->，可得12b <． 又由()111,FA x y =-，()221,FB x y =-，可得()()()1212121212111FA FB x x y y x x x x y y ⋅=--+=-+++ ()22111123044b b b b b =--++=+=，得0b =（舍去）或12b =-．由12b =-，可得1213x x +=，1236x x =，所以AB ===()()121211215AF BF x x x x +=+++=++=，故ABF 的周长为15+ 【点睛】本题考查了直线与抛物线的位置关系，考查了抛物线的定义，韦达定理和弦长公式，考查了运算求解能力，属于中档题.。

一轮复习数学模拟试题05满分150分，用时120分钟． 第一部分 选择题（共40分）一﹑选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．1|1|2||≤+≤x x 是成立的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既非充分又非必要条2．已知函数数f (x )＝⎩⎪⎨⎪⎧2x，x >0，x ＋1，x ≤0.若f (a )＋f (1)＝0，则实数a 的值等于( )A ．－3B ．－1C ．1D ．33．等差数列{a n }的前n 项和是S n ，a 3＋a 8>0, S 9<0, 则S 1, S 2, S 3, ……,S n 中最小的是（ ）A ．S 9B ．S 8C ．S 5D ．S 44．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是（ ）Ａ．①和② Ｂ．②和③ Ｃ．③和④ Ｄ．②和④ 5．若011<<b a ，则下列不等式 ①ab b a <+；②|;|||b a >③b a <；④2>+baa b 中，正确的不等式有 （ ） A ．０个 B ．１个 C ．2个D ．３个6．将正三棱柱截去三个角（如图1所示A B C ，，分别是GHI △三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ ）7．平面α内有∠BOC=600，OA 是α的斜线，OA 与∠BOC 两边所成的角都是450，且OA=1，则E FDIA H GBC EF D AB C侧视 图1图2 BEA ．BEB ． BEC ．BED ．直线OA 与平面α所成的角的正弦值是 （ ） A ．93 B ．73 C ．33 D ．38．数列{na ＋b }中，a , b 为常数, a >0，该数列前n 项和为S n ，那么当n ≥2时有（ ）A ．S n≥n (a ＋b ) B ．S n ≤an 2＋bnC ．an 2＋bn <S n <n (a ＋b )D ．n (a ＋b )<S n <an 2＋bn第二部分 非选择题（共110分）二、填空题：本大题共6小题，每小题5分，满分30分． 9．函数y ＝16－x －x2的定义域是________． 10．若平面向量α，β满足|α|＝1，|β|≤1，且以向量α，β为邻边的平行四边形的面积为12，则α与β的夹角θ的取值范围是________．11．已知x ＝11，则1102112311222++++++++x x x x x x ΛΛ＝ . 12．若数列{a n }满足a 1＝5, a n ＋1＝22)(21nn n a a a ++(n ∈N )，则其前10项和是_____. 13．已知在平面直角坐标系中，O (0,0)，M (1,1)，N (0,1)，Q (2,-3)，动点P (x ，y )满足不等式0 ≤OP →·OM → ≤1,0≤OP →·ON → ≤1，则z ＝OQ →·OP →的最大值为____________．14．已知集合A ＝2{|-5+40}x x x ≤与B ＝2{|-2++20}x x ax a ≤，若B A ⊆,则a 的范围是_______三、解答题：本大题共6小题，满分80分．解答须写出文字说明，证明过程或演算步骤． 15.（本题满分12分）已知函数f (x )＝2cos x sin(x ＋π3)－32.(Ⅰ)求函数f (x )的最小正周期T ；(Ⅱ)若△ABC 的三边a ，b ，c 满足b 2＝ac ，且边b 所对角为B ，试求cos B 的取值范围，并确定此时f (B )的最大值．16. (本小题满分12分) 在ABC ∆，已知2233AB AC AB AC BC ⋅=⋅=u u u r u u u r u u u r u u u r ，求角A ，B ，C的大小．17. （本题满分14分）某单位建造一间地面面积为12m 2的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x 不得超过a 米，房屋正面的造价为400元/m 2,房屋侧面的造价为150元/m 2，屋顶和地面的造价费用合计为5800元，如果墙高为3m ，且不计房屋背面的费用． （Ⅰ）把房屋总造价y 表示成x 的函数，并写出该函数的定义域. （Ⅱ）当侧面的长度为多少时，总造价最底？最低总造价是多少？18．(本小题满分14分)如图，在三棱锥P ABC -中，PA ⊥底面,,60,90ABC PA AB ABC BCA ︒︒=∠=∠=， 点D ，E 分别在棱,PB PC 上，且//DE BC（Ⅰ）求证：BC ⊥平面PAC ；（Ⅱ）当D 为PB 的中点时，求AD 与平面PAC 所成的角的正弦值； （Ⅲ）是否存在点E 使得二面角A DE P --为直二面角？并说明理由.19. （本题满分14分）已知f (x )＝a 1x ＋a 2x 2＋a 3x 3＋……＋a n x n，且a 1, a 2, a 3,……,a n 组成等差数列(n 为正偶数)，又f (1)＝n 2, f (－1)＝n ,(Ⅰ) 求数列的通项公式a n ； (Ⅱ) 试比较f (21)与3的大小，并说明理由．20．（本题满分14）已知a ，b 为常数，且a ≠0，函数f (x )＝－ax ＋b ＋ax ln x ，f (e)＝2（e=2.71828…是自然对数的底数） (Ⅰ)求实数b 的值；(Ⅱ)求函数f (x )的单调区间；(Ⅲ)当a ＝1时，是否同时存在实数m 和M (m <M )，使得对每一个t ∈[m ，M ]，直线y ＝t 与曲线y ＝f (x )⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤1e ，e 都有公共点？若存在，求出最小的实数m 和最大的实数M ；若不存在，说明理由．答案一、选择题：BACD CACD二、填空题：9.{|-3<<2}x x 10. ⎣⎢⎡⎦⎥⎤π6，5π6 11. 22112. 50 13. 2 14．18(1]7-，三、解答题：本大题共6小题，满分80分．解答须写出文字说明，证明过程或演算步骤． 15.（本题满分12分）解：(1)f (x )＝2cos x ·sin(x ＋π3)－32＝2cos x (sin x cosπ3＋cos x sinπ3)－32＝2cos x (12sin x ＋32cos x )－32＝sin x cos x ＋3·cos 2x －32＝12sin2x ＋3· 1＋cos2x 2－32 ＝12sin2x ＋32cos2x ＝sin(2x ＋π3) ……………………………5分∴T ＝2π|ω|＝2π2＝π……………………….6分 (2)由余弦定理cos B ＝a 2＋c 2－b 22ac 得，cos B ＝a 2＋c 2－ac2ac＝a 2＋c 22ac －12≥2ac 2ac －12＝12，∴12≤cos B ＜1，………………………9分而0＜B ＜π，∴0＜B ≤π3.函数f (B )＝sin(2B ＋π3)，……………….10分∵π3＜2B ＋π3≤π，当2B ＋π3＝π2，即B ＝π12时，f (B )max ＝1………………………………………………12分16. (本小题满分12分) 解：设,,BC a AC b AB c ===由2AB AC AC ⋅=⋅u u u r u u u r u u r u u u r 得2cos bc A =，所以cos A =又(0,),A π∈因此6A π=……………………3分23AB AC BC ⋅=u u r u u u r 得2bc =，于是2sin sin C B A ⋅=-所以5sin sin()6C C π⋅-=，1sin (cos )2C C C ⋅=，因此22sin cos 220C C C C C ⋅+=-=，既sin(2)03C π-=………………………..9分由A=6π知506C π<<，所以3π-，4233C ππ-<，从而20,3C π-=或2,3C ππ-=，既,6C π=或2,3C π=故2,,,636A B C πππ===或2,,663A B C πππ===………………………12分17. （本题满分14分）（1）由题意可得，123(2150400)5800y x x =⨯+⨯+)0(5800)16(900a x xx ≤<++=….4分（2）58001629005800)16(900+⨯⨯≥++=xx x x y =13000 当且仅当xx 16=即4=x 时取等号。

一轮复习数学模拟试题08一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项. 1．已知全集R U =，集合A ＝{y | y ＝2x ，x ∈R }，则A C U ＝A ．∅B ．(0，＋∞)C ． (－∞，0]D ．R2．已知a ，b 是实数，则“⎩⎨⎧>>32b a ”是“5>+b a ”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．若某程序框图如图所示，则该程序运行后输出的值是 A ．4 B ．5 C ．6D ．74. 已知直线l ，m 和平面α， 则下列命题正确的是A ．若l ∥m ，m ⊂α，则l ∥αB ．若l ∥α，m ⊂α，则l ∥mC ．若l ⊥m ，l ⊥α，则m ∥αD ．若l ⊥α，m ⊂α，则l ⊥m 5．已知是虚数单位，复数ii+3＝ A ．i 103101+B ．i 103101+-C ．i 8381+-D ．i 8381--6． 函数y ＝sin (2x ＋π4)的图象可由函数y ＝sin 2x 的图象 A ．向左平移π8个单位长度而得到 B ．向右平移π8个单位长度而得到C ．向左平移π4个单位长度而得到D ．向右平移π4个单位长度而得到7．若实数x ，y 满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 则2x ＋4y 的最小值是A ．6B ．4C ．2-D ．6-8． 对于直角坐标平面内的任意两点11(,)A x y 、22(,)B x y ，定义它们之间的一种“距离”： ‖AB ‖=1212x x y y -+-，给出下列三个命题：①若点C 在线段AB 上，则‖AC ‖+‖CB ‖=‖AB ‖；(第3题图)(第15题图）②在△ABC 中，若∠C =90°，则‖AC ‖+‖CB ‖=‖AB ‖； ③在△ABC 中，‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A.0B.1C.2D.3二、填空题：本大题共7小题，每小题5分，满分30分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置. （一）必做题（9-13题） 9．函数=y xxsin 的导函数='y ． 10．在递增等比数列{a n }中，4,2342=-=a a a ，则公比q ＝．11．某学校三个社团的人员分布如下表（每名同学只参加一个社团）：学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则这三个社团人数共有_______________. 12．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝3π，3=b ，若△ABC 的面积为233 ，则c =．13．如图，F 1，F 2是双曲线C ：22221x y a b-=(a ＞0，b ＞0) 的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若 | AB |:| BF 2 |:| AF 2 |＝3 : 4 : 5，则双 曲线的离心率为.（二）选做题（14-15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在直角坐标系x O y 中，已知曲线1C ：⎩⎨⎧-=+=t y t x 212 , (为参数）与曲线2C ：⎩⎨⎧==θθsin 3cos 3y x ,（θ为参数）相交于两个点A 、B ，则线段AB 的长为. 15．（几何证明选讲选做题）如图，PAB 、PCD 为⊙O 的两条割线， 若PA=5，AB=7，CD=11，AC=2，则BD 等于.xy OA BF 1F 2(第13题图)三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）设向量a ＝)sin ,2(θ，b ＝)cos ,1(θ，θ为锐角． （1）若a ·b ＝136，求sin θ＋cos θ的值； （2）若a ∥b ，求sin(2θ＋π3)的值．17．（本小题满分12分）某中学校本课程共开设了A ，B ，C ，D 共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：（1）求这3名学生选修课所有选法的总数；（2）求恰有2门选修课没有被这3名学生选择的概率； （3）求A 选修课被这3名学生选择的人数的数学期望.18．（本小题满分14分）已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形（1）求证：N B C BC 11//平面；（2）求证：BN 11C B N ⊥平面； （3）设M 为AB 中点，在BC 边上找一点P ，使MP //平面1CNB ,并求PCBP的值.19．(本题满分14分)已知椭圆C ：)0(12222>>=+b a by a x ，左、右两个焦点分别为1F 、2F ，上顶点),0(b A ，21F AF ∆为正三角形且周长为6.8 侧视图俯视图4（1）求椭圆C 的标准方程及离心率；（2）O 为坐标原点，P 是直线A F 1上的一个动点，求||||2PO PF +的最小值，并求出此时点P 的坐标．20．(本小题满分14分)已知函数21()22f x ax x =+，()g x lnx =. （1）如果函数()y f x =在[1,)+∞上是单调减函数，求a 的取值范围；（2）是否存在实数0a >，使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根？若存在，请求出a 的取值范围；若不存在，请说明理由．21．（本题满分14分）已知正项数列{}n a 的前n 项和为n S ，且(2)4n n n a a S +=*()n ∈N . （1）求1a 的值及数列{}n a 的通项公式；（2）求证：33331231111532n a a a a ++++<*()n ∈N ； （3）是否存在非零整数λ，使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立？若存在，求出λ的值；若不存在，说明理由.参考答案(第15题图）一、选择题：CABD AADB 二、填空题： 9．函数=y xxsin 的导函数='y ． 10．在递增等比数列{a n }中，4,2342=-=a a a ，则公比q ＝．11．某学校三个社团的人员分布如下表（每名同学只参加一个社团）：学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则这三个社团人数共有_______________. 12．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝3π，3=b ，若△ABC 的面积为233 ，则c =．13．如图，F 1，F 2是双曲线C ：22221x y a b-=(a ＞0，b ＞0) 的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若 | AB |:| BF 2 |:| AF 2 |＝3 : 4 : 5，则双 曲线的离心率为.（二）选做题（14-15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在直角坐标系x O y 中，已知曲线1C ：⎩⎨⎧-=+=t y t x 212 , (为参数）与曲线2C ：⎩⎨⎧==θθsin 3cos 3y x ,（θ为参数）相交于两个点A 、B ，则线段AB 的长为. 15．（几何证明选讲选做题）如图，PAB 、PCD 为⊙O 的两条割线， 若PA=5，AB=7，CD=11，AC=2，则BD 等于.9、2sin cos xxx x - 10、2 11、150 12、 713、13 14、 4 15、 6 三、解答题：12+12+14+14+14+14=80xy OA BF 1F 2(第13题图)16．（本小题满分12分）设向量a ＝)sin ,2(θ，b ＝)cos ,1(θ，θ为锐角． （1）若a ·b ＝136，求sin θ＋cos θ的值； （2）若a ∥b ，求sin(2θ＋π3)的值．17．（本小题满分12分）某中学校本课程共开设了A ，B ，C ，D 共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：（1）求这3名学生选修课所有选法的总数；（2）求恰有2门选修课没有被这3名学生选择的概率； （3）求A 选修课被这3名学生选择的人数的数学期望.18．（本小题满分14分）已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形（1）求证：N B C BC 11//平面；（2）求证：BN 11C B N ⊥平面； （3）设M 为AB 中点，在BC 边上找一点P ，使MP //平面1CNB ,并求PCBP的值.19．(本题满分14分)已知椭圆C ：)0(12222>>=+b a by a x ，左、右两个焦点分别为1F 、2F ，上顶点),0(b A ，21F AF ∆为正三角形且周长为6.（1）求椭圆C 的标准方程及离心率；（2）O 为坐标原点，P 是直线A F 1上的一个动点，求||||2PO PF +的最小值，并求出8 主视图 侧视图俯视图4此时点P 的坐标．20．(本小题满分14分)已知函数21()22f x ax x =+，()g x lnx =. （1）如果函数()y f x =在[1,)+∞上是单调减函数，求a 的取值范围；（2）是否存在实数0a >，使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根？若存在，请求出a 的取值范围；若不存在，请说明理由．21．（本题满分14分）已知正项数列{}n a 的前n 项和为n S ，且(2)4n n n a a S +=*()n ∈N . （1）求1a 的值及数列{}n a 的通项公式；（2）求证：33331231111532n a a a a ++++<*()n ∈N ； （3）是否存在非零整数λ，使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立？若存在，求出λ的值；若不存在，说明理由.三、解答题： 16．（本小题满分12分）解：（1）因为a ·b ＝2＋sin θcos θ＝136，所以sin θcos θ＝16． ……………… 3分所以 (sin θ＋cos θ)2＝1＋2 sin θcos θ＝43．又因为θ为锐角，所以sin θ＋cos θ＝233． ………………6分 （2） 解法一 因为a ∥b ，所以tan θ＝2． ………………8分 所以 sin2θ＝2 sin θcos θ＝2 sin θcos θsin 2θ＋cos 2θ＝ 2 tan θtan 2θ＋1＝45， cos2θ＝cos 2θ－sin 2θ＝cos 2θ－sin 2θsin 2θ＋cos 2θ＝1－tan 2θtan 2θ＋1＝－35．………………10分 所以sin(2θ＋π3)＝12sin2θ＋32cos2θ＝12×45＋32×(－35 )＝4－3310． ………………12分解法二 因为a ∥b ，所以tan θ＝2． ………………8分 所以 sin θ＝255，cos θ＝55．因此 sin2θ＝2 sin θcos θ＝45， cos2θ＝cos 2θ－sin 2θ＝－35． ………………10分 所以sin(2θ＋π3)＝12sin2θ＋32cos2θ＝12×45＋32×(－35 )＝4－3310． ………………12分17、（本小题满分12分）解析：(Ⅰ)每个学生有四个不同选择，根据乘法法则，选法总数N=64444=⨯⨯……3分 (Ⅱ) 恰有2门选修课这3名学生都没选择的概率为1694442332432223242=⨯⨯⨯⨯⨯==A C C P ………………7分(Ⅲ) 设A 选修课被这3名学生选择的人数为ξ，则ξ＝0,1,2,3P(ξ＝0)＝64274333= P(ξ＝1)＝6427433213=⋅C P(ξ＝2)＝64943313=⋅C P(ξ＝3)＝ 6414333=C ………………9分ξ的分布列是…………10分43641364926427164270=⨯+⨯+⨯+⨯=ξE …………12分18.解：（1）证明： 该几何体的正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，∴1,,BB BC BA 两两互相垂直。

一轮复习数学模拟试题07一选择题（每个5分共12题60分）1、函数1()ln(1)f x x =++ （ ）A ．[2,0)(0,2]-B ． (1,0)(0,2]-C ．[2,2]-D ．(1,2]-2、,a b 为非零向量，“函数2()()f x ax b =+ 为偶函数”是“a b ⊥”的( )A. 充分但不必要条件B. 必要但不充分条件C. 充要条件D. 既不充分也不必要条件3、双曲线222298x y -=-则其焦点坐标为（ ） A ． ()5,0± B. ()3,0± C. ()0,3± D. ()0,5±4、6名选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有（ ） A ．480种 B ．360种 C ．240种 D ．720种5、已知各项均为均为正数的等比数列中，13213,,22a a a 成等差数列，则1113810a a a a +=+（ ） A ． -1或 3 B. 3 C. 27 D. 1或27 6、设ABC ∆的三个内角A,B,C 向量(3s i n ,s i n ),(c o s ,3c o s )m A B n B A ==若1cos()mn A B ⋅=++则C=（）A ．6πB 。

3π C 。

23π D 。

56π 7、已知某个三棱锥的三视图如图所示，其中正视图是等边三 角形，侧视图是直角三角形，俯视图是等腰直角三角形，则此三棱锥的体积等于A8、1,,0,1,ax y a x y x y>+=+设且的最小值为4则a=（ ） A ．1 B.2 C.3 D.49、设m 、n 是不同的直线，α、β、γ是不同的平面，有以下四个命题：（1）//////αββγαγ⎫⇒⎬⎭（2）//m m αββα⊥⎫⇒⊥⎬⎭（3）//m m ααββ⊥⎫⇒⊥⎬⎭（4）////m n m n αα⎫⇒⎬⊂⎭，其中，假命题是A.（1）（2）B.（2）（3） C 。

高考数学三轮复习冲刺模拟试题02函数01一、选择题1 ．已知函数12x f (x )x x ,g(x )x ,h(x )x ln x =--=+=+的零点分别为x 1，x 2，x 3，则 （ ）A ．x 1<x 2<x 3B ．x 2<x 1<x 3C ．x 3<x 1<x 2D ．x 2<x 3<x 12 ．己知函数1f (x )+是偶函数，当1x (,)∈-∞时，函数f (x )单调递减，设1122a f (),b f (),c f ()=-=-=，则a ，b ，c 的大小关系为（ ）A ．c<a<bB ．a<b<cC ．a<c<bD ．c<b<a 3 ．试题）定义在R 上的函数满足，当时，，则（ ）（ ）A ．B ．C ．D ．4 ．已知函数的图象如图所示则函数的图象是（ ）5 ．函数的定义域为（ ）（ ）A ．B ．C ．D ．6 ．设函数1()ln (0)3f x x x x =->,则函数()f x（ ）A ．在区间(0,1)(1,)+∞，　内均有零点B ．在区间(0,1)(1,)+∞，　内均无零点C ．在区间(0,1)内有零点,在区间(1,)+∞内无零点D ．在区间(0,1)内无零点,在区间(1,)+∞内有零点7 ．定义在R 上的奇函数f(x),当x≥0时,f(x)=⎪⎩⎪⎨⎧+∞∈∈+）,1[3-x -1)1,0[x ），1x （log 21x ,则关于x 的函数F(x)=f(x)-a(0<a<1)的所有零点之和为 （ ）A ．2a -1B ．1-2aC ．2-a -1D ．1-2-a8 ．设)(x f 是定义在R 上的周期函数,周期为4=T ,对R x ∈都有)()(x f x f =-,且当]0,2[-∈x 时,121)(-⎪⎭⎫⎝⎛=xx f ,若在区间]6,2(-内关于x 的方程)2(log )(+-x x f a =0)1(>a 恰有3个不同的实根,则a 的取值范围是 （ ）A ．(1,2)B ．),2(+∞C ．()4,1D ．()32,49 ．已知函数()=ln f x x ，则函数()=()'()g x f x f x -的零点所在的区间是（ ）A ．（0,1）B ．（1,2）C ．（2,3）D ．（3,4）10．定义域为R 的函数()f x 满足(+2)=2()f x f x ，当x ∈[0，2)时，2|x-1.5|-,[0,1)()=-(0.5),[1,2)x x x f x x ⎧∈⎨∈⎩若[-4,-2]x ∈时，1()-42t f x t ≥恒成立，则实数t 的取值范围是（ ）A ．[-2，0)U (0，l)B ．[-2，0) U [l ，+∞)C ．[-2，l]D ．(-∞，-2]U (0，l]11．在下列区间中，函数()=+43xf x e x -的零点所在的区间为（ ）A ．（1-4，0） B ．（0，14） C ．（14，12） D ．（12，34） 12．定义在R 上的偶函数f(x),当x ∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是（ ） A ．f(π)>f(-3)>f(-2)B ．f(π)>f(-2)>f(-3)C．f(π)<f(-3)<f(-2) D．f(π)<f(-2)<f(-3)13．偶函数f（x）满足(1)(1)f x f x+=-，且在x∈[0，1]时，f（x）=x2，则关于x的方程f（x）=x⎪⎭⎫⎝⎛101在10[0,]3上根的个数是（）A．1个B．2个C．3个D．5个14．设5log4a=, 25(log3)b=,4log5c=，则（）A．a<c<b B．b<c<a C．a<b<c D．b a c<<15．设函数1(1)|-1|)=1(=1)xxf xx⎧≠⎪⎨⎪⎩（，若关于x的方程2[()]+()+c=0f x bf x有三个不同的实数根123,,x x x，则222123++x x x等于（）A．13 B．5 C．223c+2cD．222b+2b16．函数()f x的定义域为R，若(1)f x+与(1)f x-都是奇函数，则（）A．()f x是偶函数B．()f x是奇函数C．()(2)f x f x=+D．(3)f x+是奇函数17．给定函数①12=y x-，②23+3=2x xy-，③12=log|1-|y x，④=sin2xyπ，其中在(0,1)上单调递减的个数为（）A．0 B．1 个C．2 个D．3个18．已知定义在区间[0,2]上的函数=()y f x的图象如图所示，则=(2-)y f x的图象为19．已知函数()()2531m f x m m x --=--是幂函数且是()0,+∞上的增函数，则m 的值为（ ）A ．2B ．－1C ．－1或2D ．020．已知函数2342013()12342013xx x x f x x =+-+-++L L ,2342013()12342013x x x x g x x =-+-+--L L ,设函数()(3)(4)F x f x g x =+⋅-,且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内,则-b a 的最小值为 （ ）A ．8B ．9C ．10D ．1121．函数21(0)()(1)(0)x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不等的实数根,则实数a 的取值范围为 （ ）A ．(-∞,0)B ．[0,1)C ．(-∞,1)D ．[0,+∞)22．函数x x x f 2log 12)(+-=的零点所在的一个区间是（ ）A ．⎪⎭⎫⎝⎛41,81 B ．⎪⎭⎫⎝⎛21,41 C ．⎪⎭⎫⎝⎛1,21 D ．)2,1(23．若直角坐标平面内的两点P 、Q 满足条件：①P 、Q 都在函数)(x f y =的图像上；②P 、Q关于原点对称，则称点对[P ,Q]是函数)(x f y =的一对“友好点对”（注：点对[P ,Q]与[Q,P]看作同一对“友好点对”）.已知函数⎩⎨⎧≤-->=)0(4)0(log )(22x x x x x x f ，则此函数的“友好点对”有（ ）A ．0对B ．1对C ．2对D ．3对参考答案一、选择题 1. D 2. A3. 【答案】D【解析】由题意可知，函数的图象关于y 轴对称，且周期为2，故可画出它的大致图象，如图所示：∵且,而函数在是减函数， ∴，选D.4. 【答案】A【解析】由函数的两个根为.x a x b ==，图象可知01,1a b <<<-。

广东省中山市（新版）2024高考数学统编版模拟(预测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题已知函数，则的解集是（）A．B．C．D．第(2)题下列说法①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；②设有一个回归方程，变量增加1个单位时，平均增加5个单位；③线性回归方程必过点；④设具有相关关系的两个变量，的相关系数为，则越接近于0，，之间的线性相关程度越高；其中错误的个数是（）A．3B．2C．1D．0第(3)题如图位于西安大慈恩寺的大雁塔是我国现存最早､规模最大的唐代四方楼阁式砖塔，其最高处的塔刹可以近似地看成一个正四棱锥，已知正四棱锥的高为，其侧棱与底面的夹角为，则该正四棱锥的体积约为（）A．B．C．D．第(4)题某三棱柱的三视图如图所示，该三棱柱的体积为（）A．B．C．D．第(5)题已知函数，其中表示不超过的最大整数．设，定义函数：，，，，则下列说法正确的有个①的定义域为；②设，，则；③；④若集合，则中至少含有个元素．A．个B．个C．个D．个第(6)题记等差数列的前项和为，则（）A．14B．72C．36D．60第(7)题若复数满足.则（）A．B．C．D．第(8)题若函数在上单调递增，则的取值范围为（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知是两个虚数，则下列结论中正确的是（）A．若，则与均为实数B．若与均为实数，则C．若均为纯虚数，则为实数D．若为实数，则均为纯虚数第(2)题已知所有顶点在两个平行平面内的多面体叫作拟柱体，在这两个平面内的面叫作拟柱体的底面，其余各面叫作拟柱体的侧面，到上、下底面距离相等的截面叫作中截面．现有拟柱体，其中上、下底面均为边长为2的正方形，分别为底面和底面的中心，与两底面垂直，且，则（）A．拟柱体外接球的表面积为B．直线与平面所成角满足C．拟柱体的中截面面积的最大值为D．拟柱体的侧面为全等的三角形第(3)题已知在平面直角坐标系中，，，，，，P为该平面上一动点，记直线PD，PE的斜率分别为和，且，设点P运动形成曲线F，点M，N是曲线F上位于x轴上方的点，且，则下列说法正确的有（）A．动点P的轨迹方程为B．△PAB面积的最大值为C．的最大值为5D．的最小值为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知，则______.第(2)题二项式（x+y）5的展开式中，含x2y3的项的系数是___（用数字作答）．第(3)题对于的展开式，含项的系数为________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知抛物线的焦点为，直线与抛物线交于两点，其中两点的横坐标之积为．(1)求的值；(2)若在轴上存在一点，满足，求的值．第(2)题设函数在上有定义，实数和满足.若在区间上不存在最小值，则称在区间上具有性质P.（1）当，且在区间上具有性质P，求常数C的取值范围；（2）已知，且当时，，判别在区间上是否具有性质P；（3）若对于满足的任意实数和，在区间上具有性质P，且对于任意，当时，有：，证明：当时，.第(3)题设函数.(1)若最小值为，求的范围；(2)令，的图象上有一点列，若直线的斜率为，证明：.第(4)题在中,为的角平分线,且.(1)若,,求的面积;(2)若,求边的取值范围.第(5)题已知双曲线的焦距为10，且经过点．A，B为双曲线E的左、右顶点，P为直线上的动点，连接PA，PB交双曲线E于点C，D（不同于A，B）．(1)求双曲线E的标准方程．(2)直线CD是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．。

广东省中山市（新版）2024高考数学人教版真题(综合卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题已知函数，其中，，其中，则图象如图所示的函数可能是（）．A．B．C．D．第(2)题已知集合，，则（）A．B．C．D．第(3)题已知这个数字，从中取三个不同的数字，把其中最大的数字放在个位上排成三位数，这样的三位数有（）A．55个B．70个C．40个D．35个第(4)题向量，，若与共线，则（）A．B．C．D．5第(5)题已知全集，若，则（）A．1B．2C．3D．4第(6)题有一组样本数据，，，…，，由这组数据得到新样本数据，其中，，，…，，为非零常数，则（）A．两组样本数据的样本平均数相同B．两组样本数据的样本中位数数相同C．两组样本数据的样本标准差相同D．两组样本数据的样本极差不同第(7)题数列满足，（），，若数列是递减数列，则实数的取值范围是（）A．B．C．D．第(8)题若直线与圆相交于两点，且（其中为原点），则的值为（）.A．或B．C．或D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知在体能测试中，某校学生的成绩服从正态分布N（70，16），其中60分为及格线，则下列结论中正确的有（）（附：随机变量服从正态分布N（，），则）A．该校学生成绩的均值为70B．该校学生成绩的标准差为4C．该校学生成绩的标准差为16D．该校学生成绩及格率超过95%第(2)题已知双曲线的方程为，，分别为双曲线的左､右焦点，过且与x轴垂直的直线交双曲线于M，N两点，又，则（）A．双曲线的渐近线方程为B．双曲线的顶点到两渐近线距离的积的5倍等于焦点到渐近线距离的平方C．双曲线的实轴长､虚轴长､焦距成等比数列D．双曲线上存在点，满足第(3)题已知函数，则（）A．是上的增函数B．函数有且仅有一个零点C．函数的最小值为D．存在唯一个极值点三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知直线是曲线在点处的切线，则直线的方程为__________．第(2)题如图，已知椭圆的左、右焦点分别为，点M，N在上，，则的离心率为____________.第(3)题已知抛物线的焦点为F，其准线与x轴的交点为C，过F的直线与抛物线交于A，B两点，若弦AB的中点到抛物线准线的距离为18，则的余弦值为______；四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题近年来，凭借主旋律电影的出色表现，我国逐渐成为全球电影票房最高的市场．2022年十一期间热映的某主旋律电影票房超过16亿元．某研究性学习小组就是否看过该电影对影迷进行随机抽样调查，调查数据如下表（单位：人）．是否合计青年（30岁以下）45550中年（30岁（含）以351550上）合计8020100(1)是否有99%的把握认为选择看该电影与年龄有关？(2)将频率视为概率，若从众多影迷中随机抽取10人，记其中看过该电影的人数为，求随机变量的数学期望及方差．附：，其中．0.0500.0100.0013.841 6.63510.828第(2)题已知数列为等比数列，其前n项和为，且．(1)求数列的公比q和的值；(2)求证：，，成等差数列．第(3)题随着现代社会的发展，我国对于环境保护越来越重视，企业的环保意识也越来越强.现某大型企业为此建立了5套环境监测系统，并制定如下方案：每年企业的环境监测费用预算定为1200万元，日常全天候开启3套环境监测系统，若至少有2套系统监测出排放超标，则立即检查污染源处理系统；若有且只有1套系统监测出排放超标，则立即同时启动另外2套系统进行1小时的监测，且后启动的这2套监测系统中只要有1套系统监测出排放超标，也立即检查污染源处理系统.设每个时间段（以1小时为计量单位）被每套系统监测出排放超标的概率均为，且各个时间段每套系统监测出排放超标情况相互独立.（1）当时，求某个时间段需要检查污染源处理系统的概率；（2）若每套环境监测系统运行成本为300元/小时（不启动则不产生运行费用），除运行费用外，所有的环境监测系统每年的维修和保养费用需要100万元.现以此方案实施，问该企业的环境监测费用是否会超过预算(全年按9000小时计算)？并说明理由.第(4)题中，角的对边分别为，从下列三个条件中任选一个作为已知条件，并解答问题.①；②；③的面积为.(1)求角A的大小；(2)求的取值范围.注：如果选择多个条件分别解答，按第一个解答计分.第(5)题已知函数．(1)讨论的单调性，并比较与的大小；(2)若，为两个不相等的正数，且，求证：．。