第9章梁的弯曲变形与刚度计算
- 格式:ppt
- 大小:1.30 MB
- 文档页数:68


第9章__梁的挠度和刚度计算在结构分析中,梁的挠度和刚度是非常重要的参数,它们能够帮助我们了解和评估梁的性能和稳定性。
本章主要介绍了梁的挠度和刚度的计算方法。
首先,我们需要了解梁的挠度是什么。
简单来说,梁的挠度指的是梁在承受荷载时的弯曲和垂直变形程度。
挠度大小反映了梁的柔软性和变形能力,对于结构工程来说,挠度必须在允许范围内,以保证结构的安全和稳定。
梁的挠度计算可以通过简化的工程解析方法或者数值计算方法来进行。
这里主要介绍两种常用的方法。
第一种方法是基于简化的工程解析方法,即梁的挠度计算公式。
根据梁的几何形状和受力情况,可以得到不同类型梁的挠度计算公式。
例如,对于简支梁,其挠度可以用以下公式计算:δ=(5*q*L^4)/(384*E*I)其中,δ是梁的最大挠度,q是梁的单位长度荷载,L是梁的长度,E是梁的弹性模量,I是梁的截面惯性矩。
对于其他类型的梁,如悬臂梁、连续梁等,也有相应的挠度计算公式。
通过这些公式可以得到梁的最大挠度。
第二种方法是使用数值计算方法,主要是有限元法。
有限元法是一种通过将结构分割成若干小单元,然后进行位移解和力学分析的方法。
通过有限元软件,可以模拟梁在荷载作用下的变形情况,并得到挠度的数值解。
此外,在梁的挠度计算中,还需要考虑梁的边界条件。
梁的边界条件决定了梁的约束程度,也会影响梁的挠度大小。
常见的边界条件包括简支、悬臂、固支等。
在梁的刚度计算中,主要考虑的是梁的弯曲刚度和剪切刚度。
弯曲刚度指的是梁在弯曲过程中对外力的抵抗能力,可以用弯矩-曲率关系来表示。
剪切刚度指的是梁在受剪力作用下的变形能力,可以用剪力-变形关系来表示。
梁的弯曲刚度和剪切刚度分别可以通过以下公式计算:弯曲刚度:EI=M/θ剪切刚度:GA=T/ϕ其中,E是梁的弹性模量,I是梁的截面惯性矩,G是梁的剪切模量,A是梁的横截面积,M是梁的弯矩,θ是梁的曲率,T是梁的剪力,ϕ是梁的剪应变。
通过计算弯曲刚度和剪切刚度,我们可以评估梁在荷载作用下的响应和变形情况,进一步判断结构的性能和稳定性。






第9章梁的挠度和刚度计算梁的挠度和刚度是结构力学中的重要概念,它们能够帮助我们分析和设计梁结构的性能。
在这一章中,我们将讨论如何计算梁的挠度和刚度。
在梁的分析中,挠度是一个重要参数,用来描述梁在受力后产生的变形。
挠度的大小可以反映梁的刚度,即梁的抵抗变形的能力。
计算梁的挠度可以通过解析方法、数值方法和实验方法来进行。
在解析方法中,梁的挠度可以通过弯曲方程来计算。
对于简支梁的弯曲问题,我们可以使用梁的弯矩方程和挠度方程来计算梁的挠度。
对于集中载荷作用下的梁,挠度方程可以表示为:δ(x)=(F*x^2)/(6*E*I)其中,δ(x)表示距离梁端点x处的挠度,F表示施加在梁上的力,E表示梁的杨氏模量,I表示梁的截面惯性矩。
通过这个方程,我们可以计算任意位置处的梁挠度。
对于均布载荷作用下的梁,挠度方程可以表示为:δ(x)=(w*x^4)/(8*E*I)其中,w表示单位长度上施加的均布载荷。
通过这个方程,我们可以计算任意位置处的梁挠度。
数值方法是另一种计算梁挠度的常用方法,它基于数值近似和积分方法。
其中最常见的方法是有限元法。
有限元法将梁结构划分为许多小单元,并基于这些小单元的形状函数和位移函数来计算梁的挠度。
通过这种方法,我们可以得到梁在各个位置的近似挠度值。
实验方法是第三种计算梁挠度的方法。
这种方法需要在实验室使用悬臂梁等设备对梁结构进行实验。
通过施加不同的载荷并测量梁的变形,我们可以计算出梁在各个位置的挠度。
梁的刚度是另一个重要的参数,它描述了梁结构对于外部载荷的抵抗能力。
刚度通常用弹性系数表示,在梁结构中即为弹性模量。
弹性模量是梁材料的一个物理特性,它越大,则说明梁越硬,更难发生变形。
梁的刚度可以通过弯矩方程和挠度方程来计算。
对于简支梁的弯曲问题,弯矩方程可以表示为:M(x)=(F*x)/L其中,M(x)表示距离梁端点x处的弯矩,F表示施加在梁上的力,L 表示梁的长度。
通过这个方程,我们可以计算任意位置处的梁弯矩。
材料力学第9章梁的挠度和刚度计算梁的挠度和刚度计算材料力学第9章引言梁是一种常见的结构元素,在各个工程领域都有广泛的应用。
了解梁的挠度和刚度计算方法对于设计和分析梁的性能至关重要。
本文将介绍材料力学第9章中梁的挠度和刚度计算的相关内容。
1. 梁的挠度计算方法1.1 单点弯曲当梁受到单点弯曲时,可以使用梁的弯曲方程来计算梁的挠度。
梁的弯曲方程可以表达为:δ = (M * L^2) / (2 * E * I)其中,δ为梁的挠度,M为梁的弯矩,L为梁的长度,E为梁的弹性模量,I为梁的截面惯性矩。
1.2 均匀分布荷载当梁受到均匀分布荷载时,梁的挠度计算稍有不同。
可以使用梁的基本方程来计算梁的挠度。
梁的基本方程可以表达为:δ = (q * L^4) / (8 * E * I)其中,δ为梁的挠度,q为梁的均匀分布荷载,L为梁的长度,E为梁的弹性模量,I为梁的截面惯性矩。
2. 梁的刚度计算方法梁的刚度是指梁对外界荷载的抵抗能力。
梁的刚度可以通过计算梁的弯曲刚度和剪切刚度得到。
2.1 弯曲刚度梁的弯曲刚度可以通过梁的截面惯性矩来计算。
弯曲刚度可以表示为:EI = ∫(y^2 * dA)其中,EI为梁的弯曲刚度,y为离梁中性轴的距离,dA为微元面积。
2.2 剪切刚度梁的剪切刚度可以通过梁的截面两点间的剪力和相对位移关系来计算。
剪切刚度可以表示为:GJ = ∫(θ * dA)其中,GJ为梁的剪切刚度,θ为梁的剪切角,dA为微元面积。
3. 示例为了加深对梁的挠度和刚度计算的理解,下面以一根长度为L的梁为例进行计算。
假设梁受到均匀分布荷载q作用,并且梁的截面为矩形截面,梁的宽度为b,高度为h。
根据梁的挠度计算方法,可以得到梁的挠度公式为:δ = (q * L^4) / (8 * E * b * h^3)根据梁的刚度计算方法,可以得到梁的弯曲刚度和剪切刚度公式为: EI = (b * h^3) / 12GJ = (b * h * h^3) / 12通过计算梁的挠度和刚度,可以得到梁的性能参数,进而进行工程设计和分析。
材料力学第9章梁的挠度和刚度计算在工程结构中,梁是一种常见的构件,其在承受载荷时会发生弯曲变形。
而梁的挠度和刚度计算是材料力学中的重要内容,对于确保梁的正常工作和结构的安全性具有至关重要的意义。
首先,我们来理解一下什么是梁的挠度。
简单来说,梁的挠度就是梁在受力作用下,横截面形心沿垂直于轴线方向的位移。
想象一下一根水平放置的梁,在受到垂直向下的力时,它会向下弯曲,这个弯曲的程度就是挠度。
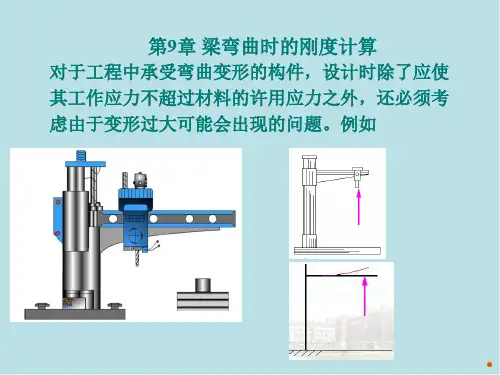
那么为什么要计算梁的挠度呢?这是因为过大的挠度可能会影响梁的正常使用功能。
比如,在桥梁结构中,如果梁的挠度过大,可能会导致桥面不平整,影响车辆行驶的舒适性和安全性;在机械零件中,过大的挠度可能会导致零件之间的配合出现问题,影响机器的正常运转。
接下来,我们谈谈梁的刚度。
梁的刚度是指梁抵抗变形的能力。
刚度越大,梁在相同载荷作用下产生的挠度就越小。
刚度与梁的材料特性(如弹性模量)、截面形状和尺寸以及梁的支撑方式等因素有关。
在计算梁的挠度时,通常需要运用一些基本的力学原理和公式。
比如,对于简单的静定梁,可以使用积分法或叠加法来求解挠度和转角方程。
积分法的基本思路是根据梁的弯曲微分方程,通过两次积分得到挠度和转角的表达式。
这个过程需要对梁的受力情况进行详细的分析,确定弯矩方程,然后进行积分运算。
叠加法则是基于线性叠加原理。
如果梁同时受到多个载荷的作用,可以先分别计算每个载荷单独作用时梁的挠度和转角,然后将这些结果进行叠加,得到最终的挠度和转角。
然而,实际工程中的梁往往比较复杂,可能是超静定梁,或者具有变截面、非均布载荷等情况。
对于这些复杂的梁,我们可能需要借助更高级的力学方法,如力法、位移法或者有限元法来进行分析。
在进行梁的挠度和刚度计算时,还需要考虑一些实际因素。
例如,材料的非线性特性在某些情况下不能忽略。
当梁所承受的载荷较大时,材料可能会进入塑性阶段,此时弹性模量不再是一个常数,需要采用相应的塑性力学理论进行分析。
另外,温度变化也可能会对梁的挠度产生影响。
第9章弯曲刚度问题9.1 基本概念9.1.1 梁弯曲后的挠曲线吊车梁若变形过大,将使小车行走困难,还会引起梁的严重振动。
因此,必须对梁的变形加以限制若梁的变形在弹性范围内,梁的轴线在梁弯曲后变为一条连续光滑曲线,该曲线称为弹性曲线或挠度曲线,简称弹性线或挠曲线。
挠曲线:梁变形后的轴线。
性质:连续、光滑、弹性、极其平坦的平面曲线。
9.1.2梁的挠度与转角设有一具有纵向对称面的悬臂梁,在自由端处作用一集中力F p。
F p力作用在梁的纵向对称面内,使梁发生平面弯曲。
一、挠度与转角梁的变形可用以下两个基本量来度量。
tan"二dw ,、w(x)二 w ‘ dxtan0-W⑴挠度挠度:横截面形心沿垂直于轴线方向的位移梁轴线上各点(各截面)的挠度w 随着点(截面)的位置 x 的不同而改变,即各截面的挠度是截面位置坐标x 的函数。
因小变形时,u 与w 相比为高阶无穷小,故忽略不计。
、挠度w 于转角二间的关系w = w(x)d挠曲线方程 单位:mm挠度 w 符号规定:向下为正⑵转角,向上为负。
转角:横截面绕中性轴转过的角度。
用“,”表示。
梁不同横截面其转角是不相同的,二是横截面位置坐标x 的函数 6 = &(兀)转角方程 单位:rad71的符号规定:由变形前的横截面转到变形后,顺时针为正;逆时针为负。
⑶ 水平位移:横截面形心沿水平方向的位移,用 u 表示。
9.2 小挠度微分方程及其积分9.2.1 小挠度微分方程1梁发生平面弯曲时,其轴线由直线变成一条曲率为7的平面曲线1 M 1 M (x)纯弯曲EI细长梁横力弯曲(x) El12d w d2w M(x)2dx2El 由高数知(x)dxM (x)与W的符号总是相反的JElM (x)dx C _______ 转角方程dw w解上二阶微分方程可求得挠度 w ,再根据dx,可求得截面转角71。
等截面梁:EI =常数。
Elw …M (x) Elw dx …M (x)dxElw = El — - 严(x)dx C Elw dx 二[j M (x)dx]dx Cdx Elw 二 」| M (x)dx]dx Cx Dd 2w M (x) dx 2 El尸EIw” = -M (工)求梁的变形:d 2w Eldx 2-M (x)挠曲线近似微分方程1 5 / 28w[ M (x)dx]dx Cx DE| i i ''____ 挠度方程其中C 、D 为积分常数。