轴对称与中心对称
- 格式:doc
- 大小:566.21 KB
- 文档页数:13

轴对称与中心对称的基本概念轴对称与中心对称是数学中常见的概念,用来描述物体的对称性。
在几何学中,轴对称和中心对称是两种最基本的对称方式。
本文将介绍轴对称和中心对称的概念、特点以及其在几何学和其他领域中的应用。
一、轴对称轴对称是指物体相对于某根轴按照一定的规律做对称变换时,可以将物体完全重合的情况。
这根轴称为轴对称的轴线,物体上的任意一点相对于轴线的对称点都在轴线的同一侧。
轴对称的特点:1. 轴对称的图形可以分为左右对称、上下对称或者同时存在左右和上下对称。
2. 轴对称的图形可以通过沿着轴线将一个部分复制到另一部分来得到。
3. 轴对称的图形可以在平面上无限延伸,不会受到轴线本身长度的限制。
4. 轴对称的图形可以通过旋转180度来映射到自身。
轴对称在几何学中的应用:1. 用来描述平面上的多边形、图形和图案的对称性。
2. 在建筑设计中考虑到建筑物的对称性,以求得美感和结构的稳定性。
3. 在工程制图和雕塑设计中,通过轴对称来保持形状的对称和均衡。
二、中心对称中心对称是指物体相对于某个中心点按照一定的规律做对称变换时,可以将物体完全重合的情况。
这个中心点称为中心对称的中心,物体上的任意一点都有与中心对称的一点。
中心对称的特点:1. 中心对称的图形在任意一点相对于中心的对称点都在以中心为圆心的同一条直线上。
2. 中心对称的图形可以通过旋转180度加上绕圆心的对称变换来映射到自身。
3. 中心对称的图形对于镜像是群运算的封闭性,即两个中心对称的图形的镜像仍然是中心对称的。
中心对称在几何学中的应用:1. 用来描述平面上的圆、椭圆和其他有规则形状的图形的对称性。
2. 在生物学中,许多生物体的形状可以通过中心对称来描述,比如瓢虫的斑点和花瓣的排列。
3. 在天文学中,天体的分布和轨道常常呈现中心对称的特征。
总结:轴对称和中心对称是数学和几何学中常见的对称概念。
通过对轴对称和中心对称的特点和应用的介绍,我们可以更好地理解和应用这两种对称性。

平面解析几何中的中心对称和轴对称龙碧霞一、中心对称定义:把一个图形绕某个点旋转180o 后能与另一个图形重合。
这两个图形关于这个点对称。
这个点叫着对称中心。
性质:关于某个点成中心对称的两个图形。
对称点的连线都经过对称中心。
且被对称中心平分。
一般有三种情况。
(1) 点关于点对称。
点P (x,y )关于点M(a,b)对称的点Q 的坐标是Q(2a-x,2b-y)。
(由中点坐标公式很容易得到)如点(1.-4)关于(-2,0)对称的点是(-5.4),(2) 直线关于点对称:直线l:Ax+By+C=0 关于点P (a,b )对称的直线为l 1的方程是:A (2a-x )+B(2b-y)+C=0 .即 Ax+By-2aA-2bB-C=0。
推导过程:方法一:在直线l 上任意取一点,最好是特殊点。
如取M(0,-B C )则点M 关于点P 对称的点N 的坐标是N (2a,2b+BC ).点N l 1根据中心对称的定义。
l 11得2aA+B(2b+B C D=-2aA-2Bb-C 所以 l 1的方程是:Ax+By-2aA-2bB-C=0方法二:在直线l 上任意取两点并求出它们关于点P (a,b )对称的点.由两点式易得直线为l 1的方程是:Ax+By-2aA-2bB-C=0.方法三:设直线为l 1上任意一点为M(x,y ),其关于点P (a,b )对称的点M /(x /,y /)在直线为l 上.求出点M /的坐标后代入直线 l:Ax+By+C=0即得l 1的方程是:Ax+By-2aA-2bB-C=0例如:求直线l ;3x+y-2=0关于点A (-4,4)对称的直线l /方程。
解法一:关于点A 对称的两直线l 与l /互相平行。
于是可设l /的方程为:3x+y+C=0在直线l 上任取一点M (0,2),其关于点A 对称的点N 的坐标为N (-8,6),因为N 点在直线l /上。
所以3×(-8)+6+C=0,所以 C=18,故 直线l /的方程为 3x+y+18=0.解法二:在直线l ;3x+y-2=0上取两点M (0,2),N (1,-1)易得它们关于点A (-4。
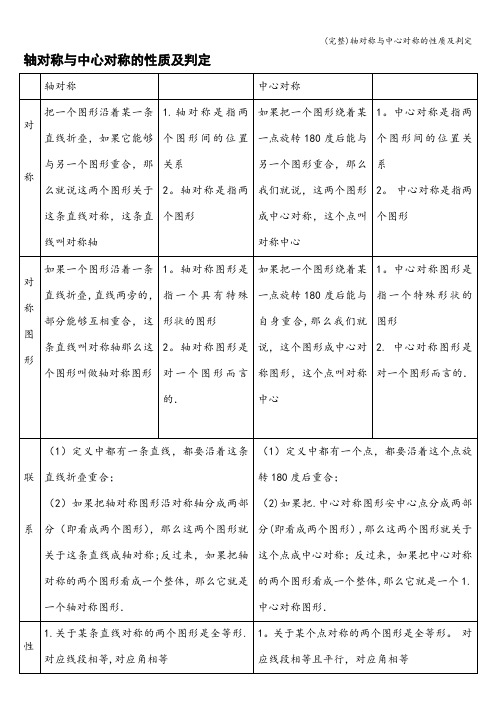

轴对称图形与中心对称图形一、轴对称1.轴对称图形定义:如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。
折痕所在的直线叫做对称轴。
2.两个图形成轴对称:对于两个图形来说,如果沿一条直线对折后,它们能完全重合,那么称这两个图形成轴对称,这条直线就是对称轴。
3.关键知识点:①轴对称是说两个图形的位置关系;而轴对称图形是说一个具有特殊形状的图形。
②成轴对称的两个图形,必定是全等图形。
4.轴对称的性质:对应点所连的线段被对称轴垂直平分;对应线段相等;对应角相等。
5.简单的轴对称作图:求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点。
后依次连结各特征点即可。
二、中心对称图形1.定义:把一个图形绕着某一点旋转180°,如果它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称。
2.中心对称和中心对称图形中心对称:如果把一个图形绕某一点旋转180度后能与另一个图形重合,这两个图形成中心对称。
中心对称图形:如果把一个图形绕某一点旋转180度后能与自身重合,这个图形是中心对称图形。
3.性质a.关于中心对称的两个图形是全等形。
b.关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
c.关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等。
三、图案的分析与设计① 首先找到基本图案,然后分析其他图案与它的关系,即由它作何种运动变换而形成。
② 图案设计的基本手段主要有:轴对称、平移、旋转三种方法。
专项练习轴对称与中心对称图形的概念:轴对称是指在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。
中心对称图形是指平面内,如果把一个图形绕某个点旋转180°后,能与自身重合,那么就说这两个图形关于这个点成中心对称。
1、(2013年潍坊市)下面的图形是天气预报中的图标,其中既是轴对称图形又是中心对称图形的是( ).A.B.C.D. BA .B .C .D .4、(2013四川南充,7,3分)有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆。

中心对称图形与轴对称图形的区别与联系中心对称是将某一个图形旋转一百八十度后,仍与原图形重合,这是中心对称;如果一个图形沿一条直线折叠,直线两侧的图形能够互相重合,这个图形就叫做轴对称图形。
中心对称图形不一定是轴对称图形,轴对称图形也不一定是中心对称图形,二者之间没有什么相互的联系。
例如:平行四边形是中心对称图形,而不是轴对称图形;等腰三角形、正五角星是轴对称图形而不是中心对称。
(轴对称图形)例如、、、和和都是轴对称图形.有的轴对称图形有不止一条对称轴,但轴对称图形最少有一条对称轴。
圆有无数条对称轴,都是经过的直线。
要特别注意的是线段,它有两条对称轴,一条是这条线段所在的直线,另一条是这条线段的中。
总之,既是轴对称图形又是中心对称图形的有:直线,线段,两条相交直线,矩形,菱形,正方形,圆等.只是轴对称图形的有:射线,角等腰三角形,等边三角形,等腰梯形等.只是中心对称图形的有:平行四边形等.既不是轴对称图形又不是中心对称图形有:不等边三角形,非等腰梯形等轴对称图形一定要沿某直线折叠后直线两旁的部分互相重合,关键抓两点:一是沿某直线折叠,二是两部分互相重合;中心对称图形是图形绕某一点旋转180°后与原来的图形重合,关键也是抓两点:一是绕某一点旋转,二是与原图形重合.旋转对称图形定义:一个图形绕着一定点旋转一定角度(小于周角)后能与自身重合.实际区别时轴对称图形要像折纸一样折叠能重合的是轴对称图形;中心对称图形只需把图形倒置,观察有无变化,没变的是中心对称图形.中心对称是旋转对称的一种特例,就是当转180度时.轴对称和中心对称、旋转对称没有必然联系.一定要沿某直线折叠后直线两旁的部分互相重合,关键抓两点:一是沿某直线折叠,二是两部分互相重合;是图形绕某一点旋转180°后与原来的图形重合,关键也是抓两点:一是绕某一点旋转,二是与原图形重合.定义:一个图形绕着一定点旋转一定角度(小于)后能与自身重合.实际区别时轴对称图形要像折纸一样折叠能重合的是轴对称图形;图形只需把图形倒置,观察有无变化,没变的是中心对称图形.中心对称是的一种特例,就是当转180度时.轴对称和中心对称、旋转对称没有必然联系。

什么是中心对称图形中心对称:在平面内,把一个图形绕着某个点旋转 180° ,如果旋转后的图形与另一个图形重合,那么就说明这两个图形的形状关于这个点成中心对称 (Central of symmetrygraph),这个点叫做它的 对称中心(Center of symmetry ),旋转180°后重合的两个点叫做 对 称点(corresponding points )。
理解中心对称的定义要抓住以下三个要素: (1 )有一个对称中心 一一点; (2 )图形绕中心旋转 180° ; (3)旋转后两图形重合. 中心对称的性质:连接中心对称图形上每一对对称点的线段都经过对称中心,且被对称中心平分 中心对称图形:在平面内,把一个图形绕着某个点旋转 180。
,如果旋转后的图形能与原来的图形重合,那么这个图形叫做 中心对称图形,这个点叫做它的 对称中心.旋转180°后重合的两个点叫做对应点(corresp onding poi nts)。
① 对称中心平分中心对称图形内通过该点的任意线段且使中心对称图形的面积被平分 (对称点在中心对称图形中)。
② 成中心对称的两个图形全等。
③ 中心对称图形上每一对对称点所连成的线段都被对称中心平分。
区分:中心对称是两个图形间的位置关系,而中心对称图形是一种具有独特特征的图 形。
中心对称图形常见图形常见的中心对称图形有:线段,矩形,菱形,正方形,平行四边形,圆,边数为偶数的正多边形,某些不规则图形等。
正偶边形是中心对称图形正奇数边形不是中心对称图形※正六角形是中心对称图形,等腰梯形不是中心对称图形,等边三角形(正三角形),至少需旋转120度,而不是180度,所以它不是中心对称图形。
反比例函数的图像双曲线是以原点为对称中心的中心对称图形什么是轴对称图形如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形(axial symmetric figure),这条直线叫做对称轴(axis of symetric);这时,我们也说这个图形关于这条直线对称。
轴对称与中心对称的概念嘿,朋友们!今天咱来聊聊轴对称和中心对称这两个有趣的概念呀。
你看啊,轴对称就好像是一个东西对着镜子,镜子里和镜子外的那部分简直一模一样,分毫不差。
就好比咱过年贴的对联,左右两边是不是看起来特别对称呀,这就是轴对称的一种体现呢!走在路上,看到那些漂亮的建筑,有的也是轴对称的呢,是不是很神奇?这就像是大自然或者建筑师跟我们开的一个小玩笑,让我们看到这种奇妙的对称之美。
再来说说中心对称,这可就更有意思啦!中心对称就像是一个东西围着一个中心点在转圈,转了一圈之后,嘿,和原来的样子又重合啦!你想想看,咱小时候玩的那种旋转木马,不就是中心对称嘛!还有那圆圆的时钟,指针不停地转呀转,也是一种中心对称呢。
轴对称和中心对称在我们生活中可太常见啦!你说要是没有这些对称,那这个世界得变得多奇怪呀。
咱穿的衣服,好多不也是有轴对称的设计嘛,这样才显得整齐好看呀。
还有那些精美的图案、花纹,很多也是利用了对称的原理呢。
咱家里用的盘子、碗,好多不也是圆形的嘛,这就是中心对称呀。
要是没有这种对称,那吃饭的时候看着都觉得别扭呢。
而且呀,对称还能给人一种稳定的感觉。
你想想看,那些歪歪扭扭不对称的东西,是不是总让人觉得不太踏实呀。
对称可不仅仅是好看,它还有很多实际的用处呢。
比如在建筑设计中,利用对称可以让建筑物更加稳固;在艺术创作中,对称可以让作品更加有美感。
哎呀呀,这对称可真是个宝呀!你说这轴对称和中心对称是不是特别神奇?它们就像是隐藏在我们生活中的小秘密,等着我们去发现,去欣赏。
它们让我们的世界变得更加有序,更加美丽。
所以呀,我们可得好好珍惜这些对称之美,好好感受它们给我们带来的奇妙体验。
这就是轴对称和中心对称,它们就在我们身边,一直陪伴着我们呢!。
轴对称与中心对称轴对称和中心对称是几何学中常用的概念,用来描述图形的对称性质。
它们在数学、物理、工程等领域中都有广泛的应用。
本文将介绍轴对称和中心对称的定义、性质以及一些实际应用。
轴对称的概念是指图形相对于某一条线对称,即图形绕某条线旋转180度后,仍能与原来的图形完全重合。
这条线被称为对称轴。
举个例子,我们可以想象一张纸上画了一个直角三角形,如果我们将纸沿着三角形的斜边对折,那么对折后的纸与原来的纸完全重合,这说明三角形是关于对称轴对称的。
中心对称是指图形相对于某一点对称,即图形绕某一点旋转180度后,仍能与原来的图形完全重合。
这个点被称为对称中心。
一个简单的例子是正方形,当我们将正方形绕着其中心旋转180度后,它仍然与原来的正方形完全一样。
轴对称和中心对称在几何学中有一些重要的性质。
首先,它们都是自反的,即一个图形关于对称轴或对称中心对称的话,它自身也是对称的。
其次,轴对称和中心对称都是可传递的,即如果图形A关于对称轴或对称中心对称,图形B关于同样的轴或中心对称,那么图形A 和图形B之间也是对称的。
轴对称和中心对称的应用非常广泛。
在艺术和设计领域,许多作品都利用了对称的美感。
建筑设计中,对称结构可以使建筑更加稳定和美观。
在化学领域,分子的对称性对于分子的性质和反应有着重要的影响。
在物理学中,对称性是研究物理定律和现象的基础。
总结起来,轴对称和中心对称是几何学中常用的概念,用来描述图形的对称性质。
它们有着自反性和传递性的特点,广泛应用于各个领域。
通过研究轴对称和中心对称,我们可以更深入地理解和应用几何学的知识。
轴对称与中心对称◆课前热身1.下列四个图形中,不是..轴对称图形的是()2.如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,则∠PBP’的度数是() A.45° B.60° C.90° D.120°3.如图,镜子中号码的实际号码是___________.4.请写出一个是轴对称图形的图形名称.答:.【参考答案】1. D2. B3.32654.圆、矩形等◆考点聚焦1.理解轴对称和轴对称图形的联系与区别,•会判断一个图形是否是轴对称图形或中心对称图形.2.掌握轴对称的基本特征,并能用这些特征解决简单的问题(如折叠).3.能用轴对称和中心对称的性质设计图案.◆备考兵法1.本节试题多以日常生活中的工艺品、商标图案、宣传画、字母、数字为材料,判断是否是轴对称图形或中心对称图形,所以应熟练掌握基本图形的轴对称性,结合实际图形进行辨认.2.在解轴对称和折叠类问题时,应知道折叠问题要用轴对称解决,•折痕就是两个重叠部分的对称轴,往往需要设未知数,利用勾股定理建立方程(组)解决.3.平面上的最短距离问题,往往要作出对称点,•利用“两点之间线段最短”解决. ◆考点链接1. 如果一个图形沿一条直线对折,对折后的两部分能 ,那么这个图形就是 ,这条直线就是它的 .2. 如果一个图形沿一条直线折叠,如果它能与另一个图形 ,那么这两个图形成 ,这条直线就是 ,折叠后重合的对应点就是 .3. 如果两个图形关于 对称,那么对称轴是任何一对对应点所连线段的 .4. 把一个图形绕着某一个点旋转 °,如果旋转后的图形能够与原来的图形 ,那么这个图形叫做 图形,这个点就是它的 .5. 把一个图形绕着某一个点旋转 °,如果它能够与另一个图形 ,那么就说这两个图形关于这个点 ,这个点叫做 .这两个图形中的对应点叫做关于中心的 .6. 关于中心对称的两个图形,对称点所连线段都经过 ,而且被对称中心所 .关于中心对称的两个图形是 图形.7. 两个点关于原点对称时,它们的坐标符号 ,即点),(y x P 关于原点的对称点1P 为 . ◆典例精析例1(内蒙古包头)下列图形中,既是轴对称图形又是中心对称图形的有( )A .4个B .3个C .2个D .1个【答案】B【解析】本题考查轴对称图形和中心对称图形的定义,轴对称图形是指将图形沿某条直线折叠,直线两旁部分能够完全重合的图形,而中心对称图形是指将图形沿某个点旋转180°后得到的图形与原图形完全重合的图形.故同时符合上面两个条件的是第1、3和4个图形,正确答案选B.例2如图,半圆A 和半圆B 均与y 轴相切于点O ,其直径CD ,EF 均与x 轴垂直,以O•为顶点,仅开口方向相反的两条抛物线分别经过点两半圆的C ,E 和D ,F ,则图中阴影部分的面积是_______. 【答案】2π【解析】 由题可知,半圆A 与半圆B 关于y 轴对称,两条抛物线关于x 轴对称,∴S 1=S 3,S 2=S 4,∴图中阴影部分的面积实际为半圆A 的面积.例3如图,已知折叠矩形的一边AD ,使得点D 落在BC 边上的点F 处,且AB=8cm ,BC=10cm ,求EC 的长.【答案】解:由折叠性质知, AF=AD=10cm ,EF=DE . 设EC=xcm ,则DE=(8-x )cm . 在Rt △ABF 中,BF=22108-=6, ∴FC=BC-BF=10-6=4cm . 在Rt△CEF 中,EF 2=EC 2+FC 2, ∴(8-x )2=x 2+42, ∴x=3.即EC 的长为3cm .【点拨】 ①折叠问题中注意它的对称性即对应边(角)的相等性;②求这类问题中的未知线段长,常设所求线段长为x ,把其他线段用含x 的代数式表示,选择一个直角三角形.根据勾股定理列方程,用方程的思想求解.拓展变式1 如图,在矩形ABCD 中,AB=4,BC=8,将矩形沿AC 对折,点D 落在D ′处,•求:(1)线段CF 的长;(2)△AFC 的面积.答案 (1)CF=5 (2)S △AFC =10拓展变式2 如图,ABCD 是矩形,AB=4cm ,AD=3cm ,把矩形沿直线AC 重叠,点B•落在E 处,连结DE .四边形ACED 是什么图形?为什么?它的面积是多少?周长是多少? 答案 四边形ACED 是等腰梯形.(理由略) 面积为19225cm 2.周长为265cm .◆迎考精练一、选择题1.(四川内江)下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )2.(辽宁锦州)下列图形中,既是轴对称图形,又是中心对称图形的是( )A B C D3.(湖北荆门)如图,Rt△ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则A DB '∠=( )A .40°B .30°C .20°D .10°4.(广东深圳)下列图形中,既是轴对称图形,又是中心对称图形的是()A B C D5.(山东烟台)视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E”之间的变换是()A.平移B.旋转C.对称D.位似6.(浙江嘉兴)判断下列两个结论:①正三角形是轴对称图形;②正三角形是中心对称图形,结果(▲)A.①②都正确 B.①②都错误C.①正确,②错误D.①错误,②正确7.(黑龙江哈尔滨)下列图形中,既是轴对称图形,又是中心对称图形的是().8.(广东省)如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个()二、填空题1.(湖北孝感)在平面直角坐标系中,有A (3,-2),B (4,2)两点,现另取一点C (1,n ),当n = 时,AC + BC 的值最小.2.(北京市)如图,正方形纸片ABCD 的边长为1,M 、N 分别是AD 、BC 边上的点,将纸片的一角沿过点B 的直线折叠,使A 落在MN 上,落点记为A ′,折痕交AD 于点E,若M 、N 分别是AD 、BC 边的中点,则A ′N= ; 若M 、N 分别是AD 、BC 边的上距DC 最近的n 等分点(2n ,且n 为整数),则A ′N=(用含有n 的式子表示)A'NM BCADE3.(湖南娄底)如图,⊙O 的半径为2,C 1是函数y =12x 2的图象,C 2是函数y =-12x 2的图象,则阴影部分的面积是 .4.(陕西省) 如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是______.三、解答题1.(湖南娄底)如图所示,每个小方格都是边长为1的正方形,以O 点为坐标原点建立平面直角坐标系.(1)画出四边形OABC 关于y 轴对称的四边形OA 1B 1C 1,并写出点B 1的坐标是 .(2)画出四边形OABC 绕点O 顺时针方向旋转90°后得到的四边形OA 2B 2C 2,并求出点C 旋转到点C 2经过的路径的长度.2.(吉林长春)图①、图②均为76 的正方形网格,点A B C 、、在格点上.(1)在图①中确定格点D ,并画出以A B C D 、、、为顶点的四边形,使其为轴对称图形.(画一个即可)(3分)(2)在图②中确定格点E ,并画出以A B C E 、、、为顶点的四边形,使其为中心对称图形.(画一个即可)(3分)AB C图①AB C图②3.(湖北恩施)恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50km AB A =,、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和1S PA PB =+,图(2)是方案二的示意图(点A 关于直线X 的对称点是A ',连接BA '交直线X 于点P ),P 到A 、B 的距离之和2S PA PB =+.(1)求1S 、2S ,并比较它们的大小; (2)请你说明2S PA PB =+的值为最小;(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.4.(广西南宁)已知ABC △在平面直角坐标系中的位置如图10所示. (1)分别写出图中点A C 和点的坐标;(2)画出ABC △绕点C 按顺时针方向旋转90A B C '''°后的△; (3)求点A 旋转到点A '所经过的路线长(结果保留π).5.(湖南益阳)如图,△ABC 中,已知∠BAC =45°,AD ⊥BC 于D ,BD =2,DC =3,求AD 的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题. 请按照小萍的思路,探究并解答下列问题:(1)分别以AB 、AC 为对称轴,画出△ABD 、△ACD 的轴对称图形,D 点的对称点为E 、F ,延长EB 、FC 相交于G 点,证明四边形AEGF 是正方形;(2)设AD =x ,利用勾股定理,建立关于x 的方程模型,求出x 的值.【参考答案】选择题1. D2. B3.D解析:本题考查轴对称的有关知识,由折叠可知,∠ACD=∠A′CD=45°,∠A=∠CA′D=50°,∴∠ADC=∠A′DC=85°,∴∠A′DB=10°,故选D.4. D5. D6. C7. D【解析】A、B均是轴对称图形但不是中心对称图形,C是中心对称图形但不是轴对称图形.只有D即是轴对称图形又是中心对称图形8.C填空题1.25-(或–0.4)2.32,21nn-(2n≥,且n为整数)3.2π4.4解答题1. 解:(1)如图:B1的坐标是(-6,2)(2)如图:L=903180π⨯⨯=32π2. 解:(1)有以下答案供参考:(2)有以下答案供参考:3. 解:⑴图10(1)中过B 作BC ⊥AP,垂足为C,则PC=40,又AP=10, ∴AC=30在Rt △ABC 中,AB=50 AC=30 ∴BC=40∴ BP=24022=+BC CPS 1=10240+⑵图10(2)中,过B 作BC ⊥AA ′垂足为C ,则A ′C=50,又BC=40∴BA'=4110504022=+由轴对称知:PA=PA'∴S 2=BA'=4110∴1S ﹥2S(2)如 图10(2),在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA' ∴MB+MA=MB+MA'﹥A'B∴S 2=BA'为最小(3)过A 作关于X 轴的对称点A', 过B 作关于Y 轴的对称点B', 连接A'B',交X 轴于点P, 交Y 轴于点Q,则P,Q 即为所求过A'、 B'分别作X 轴、Y 轴的平行线交于点G, A'B'=5505010022=+∴所求四边形的周长为55050+P XBA QYB'A'4. 解:(1)()04A ,、()31C ,;(2)图略.(3)32AC =¼9032πAA ⨯⨯'= 32π2= 5. (1)证明:由题意可得:△ABD ≌△ABE ,△ACD ≌△ACF .∴∠DAB =∠EAB ,∠DAC =∠FAC ,又∠BAC =45°,∴∠EAF =90°.又∵AD ⊥BC∴∠E =∠ADB =90°∠F =∠ADC =90°.又∵AE =AD ,AF =AD∴AE =AF .∴四边形AEGF是正方形.(2)解:设AD=x,则AE=EG=GF=x.∵BD=2,DC=3∴BE=2 ,CF=3∴BG=x-2,CG=x-3.在Rt△BGC中,BG2+CG2=BC2∴( x-2)2+(x-3)2=52.化简得,x2-5x-6=0解得x1=6,x2=-1(舍)所以AD=x=6。