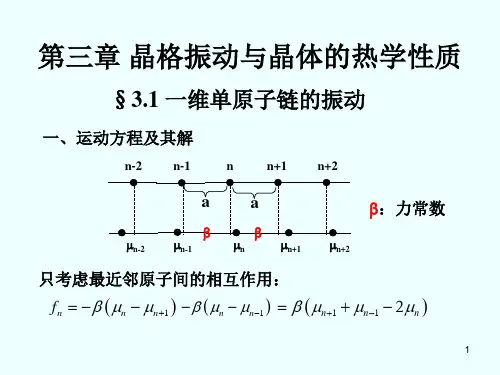
31一维晶格振动
- 格式:pdf
- 大小:940.05 KB
- 文档页数:27


一维原子链的晶格振动方程晶体是由原子或分子组成的周期性排列的结构,其内部的原子或分子通过振动相互作用,从而产生晶格振动。
晶格振动方程描述了一维原子链中原子的振动行为,对研究固体物理和材料科学具有重要意义。
一维原子链的晶格振动方程可以通过简化模型来描述。
我们假设原子链中的原子质量相同,且原子间的相互作用力为弹簧力。
在平衡位置附近,原子的位移可以用小量近似表示,即位移量远小于原子间距。
此时,可以利用胡克定律,将原子间的相互作用力近似为线性弹簧力。
根据胡克定律,弹簧的力与其伸长(或缩短)的长度成正比,且方向与伸长(或缩短)的方向相反。
对于一维原子链中相邻两个原子,其相互作用力可以表示为:F = -k(x - a) - k(x + a)其中,F为相互作用力,k为弹簧常数,x为原子的位移量,a为原子间距。
根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比。
在一维原子链中,每个原子的加速度与相邻原子的相互作用力有关,可以表示为:m(d^2x/dt^2) = -k(x - a) - k(x + a)其中,m为原子的质量,d^2x/dt^2为原子的加速度,t为时间。
将上述方程进行简化,可得:d^2x/dt^2 = -k/m * (2x - a - a)化简后得到:d^2x/dt^2 = -2k/m * (x - a/2)这就是一维原子链的晶格振动方程。
从中可以看出,原子的加速度与位移量成正比,且与原子间距和弹簧常数有关。
当原子受到外力作用时,晶格振动方程可以进一步进行修正。
一维原子链的晶格振动方程可以通过求解微分方程得到解析解,也可以通过数值模拟方法进行计算。
对于周期性边界条件下的一维原子链,可以采用傅里叶变换的方法,将晶格振动分解为一系列特定频率的波动模式。
晶格振动在固体物理和材料科学中具有广泛的应用。
通过研究晶格振动,可以揭示物质的热力学性质、电子结构和传热传电等基本行为。
此外,晶格振动还与声学性质、热导率、热膨胀和热容等宏观性质密切相关,对于材料的设计和优化具有重要意义。