第五章晶格振动习题和答案

此过程中，把什么能量表示为谐振子的能量？ 16. 什么叫声子？ 17. 讨论晶格振动时的量子力学修正体现在什幺地方？ 18． 声子有哪些性质？ 19. 什么是晶格振动的 Einsten 模型和 Debye 模型？ 20. 解释二模型与实验结果比较的原因。（重点） 21. 有人定性地认为，德拜温度θD是经典概念与量子概念解释比热的分界线，你的
不同的晶体结构，不同的B格子，可以属于相同的群，例如，B格子分别为fcc和bcc均
属于Oh群。 13. 七种晶系和十四种 B 格子是根据什么划分的？
七种晶系：B 格子的点对称性的种类数只有 7 种，称之为七种晶系。
十四种 B 格子：B 格子的空间对称性的种类数共有 14 种，称之为 14 种 B 格子。
i
a 2
(
−
k
x
+
k
y
+
k
z
)
i
a 2
(
−
k
x
+
k
y
−k
z
)
i
a 2
(
−
k
x
−k
y
+
k
z
)
i
a 2
(
−
k
x
−
)
=E
at s
－A－2B×
] a
⎡⎢ei 2 (kx +ky ) ⎣
cos
a 2
kz
+
a
ei 2(kx −kz
)
cos
a 2
kz
+
a
ei 2 (−kx
+ky
)
cos
a 2
kz

3. 下图为一晶体的晶格振动谱，此晶体为简单晶格还是复式晶格？并简单解释原因。

答：复式晶格；因为存在两支光学支，原胞应包含两个原子。

4. 根据你的理解，什么是声子？声子可以有多少种？你如
何理解声子的产生、消灭？
答：格波能量等价于一谐振子能量，是量子化的，即吸收或释放能量有一个最小单位ħ 。

声子即为格波能量的量子。

一种振动模式（或格波）对应一种声子。

N个原子组成的三维晶体对应3N种集体振动模式，即具有3N种声子。

固体内原子相互作用，从而形成不同的集体振动模式。

外界与晶格振动的相互作用，不是对某个原子的相互作用，实际上是对一种或多种振动模式的作用。

外界作用使某种振动模式的能量增加，对应声子数增加，产生声子；外界作用使某种振动模式的能量减少，对应声子数减少，声子消灭。

声子的产生和消灭就是对应振动模式能量的增加和减少。

晶格振动部分习题参考解答晶格振动部分习题参考解答9.设有一双子链最近邻原子间的力常数为和10，两种原子质量相等，且最近邻距离为a/2，求在q=0,q=aπ处的(q).并定性画出色散曲线。

m m 10 m m ____________________________________________________→←→←22aa 解：已知 21)cos 2(1212221212qa mmA ββββββω++-+=(1) 21)cos 2(12122212120a mmββββββω++-+= (2) 由题意 2＝101＝10代入（1）式得21)cos 20100(111222qa m m A ββββω++-= =21)cos 20101(11qa mm +-ββ=[]21)cos 20101(11qa m+-β当q=0时 0)1111(02=-==mq Aβω 当q=aπ时 mmaq A ββωπ2)911(2=-== 把2=101=10代入（2）式得 []21)cos 20101(1120qa m++βω＝当q=0时m q βω2202== 时aq π±= maq βωπ2020== 10.设三维晶格的光学格波在q=0的长波极限附近有i ω(q)=0－Aq 2（A0），求证光学波频率分布函数(格波密度函数)为：g()=∑-=)1(31s i 24πV2321)(0Ai ωω- i ω≤0g()=0 i ω>0证：由格波密度函数的定义已知，对一支格波在d i ω区间格波数为g (i ω)d i ω=q d d Viτπωωω+3)2(由题意可知在长波极限下等频率面为球面则g(i ω)d i ω=dq q V234)2(ππ 当i ω0ω≤时因为 q 2＝Aq i )(0ωω－ Aq q i )(0ωω-=dq=－[]2121)(2)(0q A q d i i ωωω-所以g(i ω)=2121)(214)2(003i i A A V ωωωωππ--?-??= －2321204)(AV i πωω- 由模式密度的物理意义，取其绝对值而当i ω>0ω时因为i ω＝0ω－Aq 2 所以Aq 2=0ω－i ω 又因为 A >0 q 2>0 (因为q 本身为实数)所以上式右边必满足0ω>i ω 即不存在i ω>0ω的格波则则 g(i ω)=0 又因为三维晶体中共要有3（S －1）支光学格波所以光学波频率分布函数为： g 21203314)()(AV i S i πωωω-=∑-= i ω≤0ωg(ω)=0 ω> 0ω 11．求一维单原子链的格波密度函数；若用德拜模型，计算系统的零点能。

.
从上式可以看出，当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量 m* 变 为 . 此时电子的加速度
a= 1 F =0
m*
,
即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反. 11. 万尼尔函数可用孤立原子波函数来近似的根据是什么?
[解答] 由本教科书的（5.53）式可知, 万尼尔函数可表示为
m* = 1 m 1 + 2Tn
Vn <1.
10. 电子的有效质量 m* 变为 的物理意义是什么?
[解答] 仍然从能量的角度讨论之. 电子能量的变化
(dE)外场力对电子作的功 = (dE)外场力对电子作的功 + (dE)晶格对电子作的功
m*
m
m
=
1 m
(dE ) 外场力对电子作的功
− (dE)电子对晶格作的功
i 2 nx
V (x) = Vne a
n
中, 指数函数的形式是由什么条件决定的?
[解答] 周期势函数 V(x) 付里叶级数的通式为
上式必须满足势场的周期性, 即
V (x) = Vneinx
n
显然
V (x + a) = Vnein (x+a) = Vneinx (eina ) = V (x) = Vneinx
Es (k)
=
E
at s
− Cs
−
Js
e ik Rn
n
即是例证. 其中孤立原子中电子的能量 Esat 是主项, 是一负值, − Cs和 − J s 是小量, 也是负 值. 13. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?

[e] 2[VO ]
1/ 3 1/ 6 [e ] (2K1 K 2 K 3 ) PO
2
此时电导率与氧分压的-1/6成正比。
• 在中氧压区，单电离和双电离同时存在，电中性方 程：
[e ] 2[VO ] [VO ]
[e]3 K1 K 2 PO1/ 2 (2 K 3 [e])
I41/acd：体心四方，[001]方向有4重螺旋轴41和与之垂直的滑移面a； [100]/[010] 方向有滑移面c，[110] 方向有滑移面d。点群4/mmm
R3c：菱方，[001]三次旋转轴；[100]/[010] 方向有滑移面c。点群3m
Fm3m：面心立方，[100]/[010]/[001]方向有反映面，在[111]方向有3重旋转轴 ，在[110]方向有反应面。点群m3m
a
D 1/2c F E
则 BE=
3 2
a 又BF=2FE
3 3
B
所以BF=
C
a
在三角形ABF中，AB2=AF2+BF2
1 2 3 2 a ( c) ( a) 2 3
2
因此，c/a=(8/3)1/2≈1.633
1.5 已知Nb为体心立方结构，其密度为8.57g/cm3，计算Nb的晶胞常数
及原子半径。 解：体心立方中一个晶胞中含有Nb个数为
O
1/ 2 O2
[VO ][ e] K2 [VO ] [V ][ e] K3 [VO ]
O
在低氧压区，以单电离为主，电中性方程为：
[e] [VO ]
1/ 2 1/ 4 [e ] ( K1 K 2 ) PO
2
因此，此时电导率与氧分压的-1/4成正比。 在高氧压区，以双电离为主，电中性方程为：

第三章 晶格振动与晶体的热学性质1.什么是简谐近似？解：当原子在平衡位置附近作微小振动时，原子间的相互作用可以视为与位移成正比的虎克力，由此得出原子在其平衡位置附近做简谐振动。

这个近似即称为简谐近似。

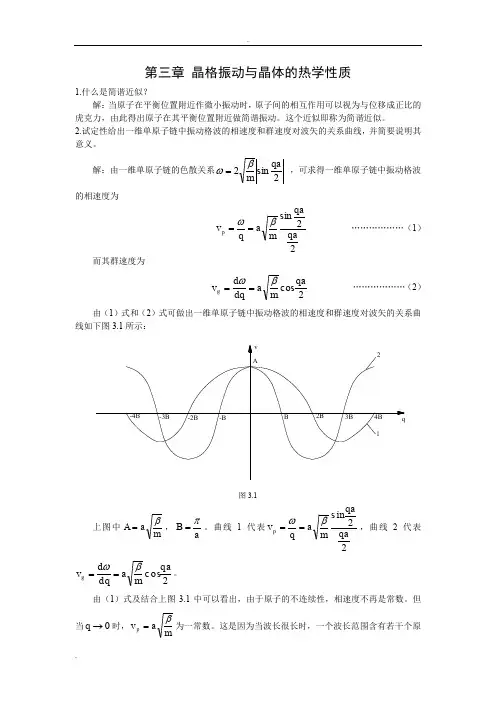
2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线，并简要说明其意义。

解：由一维单原子链的色散关系2sin2qamβω= ，可求得一维单原子链中振动格波的相速度为22sinqa qamaqv p βω== (1)2c os qam a dq d v g βω==。

由（1）式及结合上图3.1中可以看出，由于原子的不连续性，相速度不再是常数。

但当0→q 时，mav p β=为一常数。

这是因为当波长很长时，一个波长范围含有若干个原子，相邻原子的位相差很小，原子的不连续效应很小，格波接近与连续媒质中的弹性波。

由（2）式及结合上图3.1中可以看出，格波的群速度也不等于相速度。

但当0→q ，mav v p g β==，体现出弹性波的特征，当q 处于第一布区边界上，即aq π=时，0=g v ，而mav p βπ2=，这表明波矢位于第一布里渊区边界上的格波不能在晶体中传播，实际上它是一种驻波。

3.周期性边界条件的物理含义是什么？引入这个条件后导致什么结果？如果晶体是无限大，q 的取值将会怎样？解：由于实际晶体的大小总是有限的，总存在边界，而显然边界上原子所处的环境与体内原子的不同，从而造成边界处原子的振动状态应该和内部原子有所差别。

考虑到边界对内部原子振动状态的影响，波恩和卡门引入了周期性边界条件。

其具体含义是设想在一长为Na 的有限晶体边界之外，仍然有无穷多个相同的晶体，并且各块晶体内相对应的原子的运动情况一样，即第j 个原子和第j tN +个原子的运动情况一样，其中t ＝1，2，3…。

引入这个条件后，导致描写晶格振动状态的波矢q 只能取一些分立的不同值。

如果晶体是无限大，波矢q 的取值将趋于连续。

第二章：原子的结合
1． 设原子间的互作用能表示为 u (r ) 态，则 n>m. 解：原子间的相互作用能为： u (r )
作用能处于极小值： 这时有

r
m


rn
。证明：要使两原子处于平衡状

r
m


rn
。若两原子处于平衡状态时，则其相互
du (r ) (m) m 1 (n) n 1 dr r r
子晶格的情形比较， 与 q 之间存在着两种不同的色散关系。一维复式晶体中可以存在两 种独立的格波。两种不同的格波的色散关系：
2 2
(m M ) 4mM {1 [1 sin 2 aq]1 / 2 } 2 mM (m M ) (m M ) 4mM {1 [1 sin 2 aq]1 / 2 } 2 mM (m M )
xn (t ) A cos(t 2 naq) 。试求格波的色散关系。
解：一维单原子链中，牛顿方程为：
n ( x n 1 xn 1 2 xn ) m x
若将其振动位移写成 xn (t )
A cos(t 2 naq) 代入牛顿方程，则有
2

2 [1 cos(2aq)] 因此其色散关系为 m
0 。 所 以 有
r0
m

r0
m 1
n

r0
n 1
。所以
m nm r0 。 n
0
r0
同
时
有
d 2u ( r ) (m)( m 1) m 2 (n)( n 1) n 2 2 dr r r
。
所
以

半导体物理第一~第五章自测题及参考答案[1]每立方厘米(cm3)体积的硅(Si)或锗(Ge)中，Si或Ge原子个数为5.00 × 1022个或4.42 × 1022个。

Si和Ge的外层电子结构分别为3s23p2和4s24p2。

它们的价带和导带是由sp3杂化轨道形成的准连续能级构成。

那么，1 cm3硅的导带(或价带)中，准连续能级的个数为 2 × 5.00 × 1022个。

1 cm3锗的导带(或价带)中，准连续能级的个数为2 × 4.42 × 1022个。

Si和Ge的外层价电子数均为4。

那么，1 cm3的Si和Ge中价电子数分别为4 × 5.00 × 1022个和 4 × 4.42 × 1022个。

在0 K温度下，这些价电子均填空在导带还是价带（答：价带）？此时，导带中电子数和价带空穴数均为0 ，半导体呈金属性还是绝缘性（答：绝缘性）？当存在本征激发时，本征Si和Ge 的导带和价带中就会产生电子和空穴，设导带电子浓度和价带空穴浓度分别为n0和p0，那么，电中性条件为n0 = p0。

本征载流子浓度用n i表示，室温下，Si的n i相较于Ge的n i更大还是更小（答更小）？n i随温度升高而迅速增加还是减小（答：增加）？导致本征半导体的电阻率随温度升高而增加还是减小（答：减小）？[2]如果将Si的能带图画成图1形式，那么，半导体中有杂质或/和缺陷吗（答：无）？半导体是无限大吗（答：是）？其中，E c代表导带底，E v代表价带顶。

带隙宽度为E c−E v。

如果导带顶部的能量为E cʹ，则导带的能带宽度为E cʹ−E c。

E c处电子的有效质量m n∗ A (A. > 0；B. < 0；C. = 0；D. 不确定)；E v处电子的有效质量m n∗ B (A. > 0；B. < 0；C. = 0；D.不确定)；E v处空穴的有效质量m p∗ A (A. > 0；B. < 0；C. = 0；D. 不确定)图1 Si的简单能带图图2 掺杂Si的简单能带图(虚线为杂质能级)能带越宽，则能带中电子的有效质量是越大还是越小（答：越小）？相较于内层电子轨道交叠形成的能带，外层电子轨道交叠形成的能带更宽还是更窄（答：更宽）？更宽能带中的电子对导电的贡献更小还是更大（答：更大）？[3]若Si中掺杂少量Ⅴ族元素如P、As、Sb，则能带图为图2中的a，相应的半导体是p型还是n型（答：n型）？若掺杂少量Ⅴ族元素如B、Al、Ga，则能带图为图2中的b。

固体物理学答案朱建国版3HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】固体物理学·习题指导配合《固体物理学（朱建国等编着）》使用2022年4月28日第1章晶体结构 0第2章晶体的结合 (11)第3章晶格振动和晶体的热学性质 (17)第4章晶体缺陷 (26)第5章金属电子论 (30)第1章 晶体结构1.1 有许多金属即可形成体心立方结构，也可以形成面心立方结构。

从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略，并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离，试问R f /R b 等于 多少？答：由题意已知，面心、体心立方结构同一棱边相邻原子的距离相等，都设为a ：对于面心立方，处于 面心的原子与顶角原子的距离为：R f =2a对于体心立方，处于体心的原子与顶角原子的距离为：R b那么，RfRb =31.2 晶面指数为（123）的晶面ABC 是离原点O 最近的晶面，OA 、OB 和OC 分别与基失a 1，a 2和a 3重合，除O 点外，OA ，OB 和OC 上是否有格点若ABC 面的指数为（234），情况又如何答：晶面族（123）截a 1,a 2,a 3分别为1,2,3等份，ABC 面是离原点O 最近的晶面，OA 的长度等于a 1的长度，OB 的长度等于a 2长度的1/2，OC 的长度等于a 3长度的1/3，所以只有A 点是格点。

若ABC 面的指数为（234）的晶面族，则A 、B 和C 都不是格点。

1.3 二维布拉维点阵只有5种，试列举并画图表示之。

答：二维布拉维点阵只有五种类型，两晶轴b a 、，夹角 ，如下表所示。

1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵1.4 在六方晶系中，晶面常用4个指数（hkil ）来表示，如图所示，前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1，a 2，a 3上的截距a 1/h ，a 2/k ，a 3/i ，第四个指数表示该晶面的六重轴c 上的截距c/l.证明：i=-（h+k ） 并将下列用（hkl ）表示的晶面改用（hkil ）表示：（001）(133)(110)(323)（100）（010）(213) 答：证明设晶面族（hkil ）的晶面间距为d ，晶面法线方向的单位矢量为n °。

1 ⎛ d2u ⎞ 1 ⎛ d3u ⎞ ⎛ du ⎞ 2 u(a+δ ) = u(a) + ⎜ ⎟ δ + ⎜ 2 ⎟ (δ ) + ⎜ 3 ⎟ (δ )3 +⋅⋅⋅ 2 ⎝ dr ⎠a 6 ⎝ dr ⎠a ⎝ dr ⎠a
上式第一项为常数，可取为能量零点 第二项为零( f = 0)
u(a) = 0
当δ 很小, 即振动很微弱时, 可保留到第三项 则 ---简谐近似
β
m
sin
aq 2 qa 2
格波的(相)速度不再是常数 (与机械波不同)
由于原子的不连续性.
ωm
ω
ω = 2
β
m
sin
aq 2
−2π / a
Hale Waihona Puke −π / a0π/a
2π / a
q
长波近似
q= 2π
λ
→ 0, λ >> a
ω=2
β
m
sin
β aq β aq ≈2 = aq 2 m 2 m
频率与波矢为线性关系.
−M ω 2 Bei (ωt −2 naq ) = β [ Aei (ωt −2 naq −aq ) + Aei (ωt −2 naq + aq )
−M ω 2 B = β ( eiaq + e−iaq ) A − 2β B
− 2 Bei (ωt −2 naq ) ]
−mω 2 Aei (ωt −2 naq −aq ) = β [ Bei (ωt −2 naq −2 aq ) + Bei (ωt −2 naq )
格波方程
xn = A e
i (ω t − naq )
格波的意义

Cu 的费米能 Ef=7.0ev，试求电子的费米速度 Vf。在 273K 时，Cu 的电 阻率为Ρ ＝1.56×10-8Ω ·m,试求电阻的 0 平均自由时间τ 和平均自 由程 。
解：对金属处于费米面上的电子，其能量 其速度 又因为
K f m 2E f m
2K 2 E f＝ 2m
Vf＝
＝
K f＝
12.据上题，当电子浓度 n 增大时，费米球膨胀。证明当电子浓度 n 与原子浓度 na 之比 触。 解：由教材 p181 图 6－20，f.c.c 的第一 B、Z 为 14 面体，14 面体表 面离中心 T 点最近的点为 L 点。 坐标为
3 = 3 5.4/a 4 a
2 (1/2.1/2.1/2) a
2 N K＝ na






6.已知一维晶体的电子能带可写成
2 7 1 2 E( k )= ma ( 8 －coska+ 8 cos2ka)

其中 a 为晶格常数，求（1）能带宽度； （2）电子在波矢 k 状态的速度； （3）带顶和带底的电子有效质量。

解： （1）
2 7 1 2 E(k)= ma ( 8 －coska+ 8 cos2ka) 2 7 1 2 = ma 8 －coska+ 8 (2cos 2ka－1)]
(3)
沿Γ K（Kz=0, Kx= Ky=2π δ ／a，０≤δ ≤3/4）
E=Esa －A－4B（cos 2δ π ＋2cosδ π ） (4) 沿Γ W（Kz=0, Kx=2π δ ／a，Ky=π δ ／a，０≤δ ≤1） E=Esa －A－4B（cos δ π × cosδ π /2－cosδ π －cos δ π /2） 解：面心立方最近邻的原子数为 12，根据禁束缚近似 S 带计算公

目的:考核基本知识。

1、晶格常数为的体心立方晶格，原胞体积等于 C 。

A. B. C. D.2、面心立方密集的致密度是 B 。

A. 0.76B. 0.74C. 0.68D. 0.623、表征晶格周期性的概念是 A 。

A. 原胞或布拉伐格子B. 原胞或单胞C. 单胞或布拉伐格子D.原胞和基元4、晶格常数为的一维单原子链，倒格子基矢的大小为 D 。

A. B. C. D.5、晶格常数为a的简立方晶格的(010)面间距为 A 。

A. aB. 3aa D. 5a C. 46、晶格振动的能量量子称为 CA. 极化子B. 激子C. 声子D. 光子7、由N个原胞组成的简单晶体，不考虑能带交叠，则每个s能带可容纳的电子数为 C 。

A. N/2B. NC. 2ND. 4N8、二维自由电子的能态密度，与能量的关系是正比于 B 。

A. B. C. D.9、某种晶体的费米能决定于 C 。

A. 晶体的体积B.晶体中的总电子数C.晶体中的电子浓度D. 晶体的形状10、晶体结构的实验研究方法是 A 。

A. X射线衍射B.中子非弹性散射C.回旋共振D.霍耳效应1、波矢空间与倒格空间（或倒易空间）有何关系? 为什么说波矢空间内的状态点是准连续的?波矢空间与倒格空间处于统一空间, 倒格空间的基矢分别为, 而波矢空间的基矢分别为, N1、N2、N3分别是沿正格子基矢方向晶体的原胞数目.倒格空间中一个倒格点对应的体积为,波矢空间中一个波矢点对应的体积为,即波矢空间中一个波矢点对应的体积, 是倒格空间中一个倒格点对应的体积的1/N. 由于N 是晶体的原胞数目，数目巨大，所以一个波矢点对应的体积与一个倒格点对应的体积相比是极其微小的。

也就是说，波矢点在倒格空间看是极其稠密的。

因此, 在波矢空间内作求和处理时，可把波矢空间内的状态点看成是准连续的。

2、在甚低温下, 德拜模型为什么与实验相符?在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.3、解释导带、满带、价带和带隙对于导体：电子的最高填充能带为不满带，称该被部分填充的最高能带为导带，在电场中具有被部分填充的能带结构的晶体具有导电性。

半导体物理学习题答案（有目录）半导体物理习题解答目录1－1．（P32）设晶格常数为a的一维晶格，导带极小值附近能量E c（k）和价带极大值附近能量E v（k）分别为： (2)1－2．（P33）晶格常数为0.25nm的一维晶格，当外加102V/m，107V/m的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

(3)3－7．（P81）①在室温下，锗的有效状态密度Nc＝1.05×1019cm－3，Nv＝5.7×1018cm－3，试求锗的载流子有效质量mn*和mp*。

(3)3－8．（P82）利用题7所给的Nc和Nv数值及Eg＝0.67eV，求温度为300k和500k时，含施主浓度ND＝5×1015cm-3，受主浓度NA＝2×109cm-3的锗中电子及空穴浓度为多少？ (4)3－11．（P82）若锗中杂质电离能△ED＝0.01eV，施主杂质浓度分别为ND＝1014cm-3及1017cm-3，计算(1)99%电离，(2)90%电离，(3)50%电离时温度各为多少？ (5)3－14．（P82）计算含有施主杂质浓度ND＝9×1015cm-3及受主杂质浓度为1.1×1016cm-3的硅在300k 时的电子和空穴浓度以及费米能级的位置。

(6)3－18．（P82）掺磷的n型硅，已知磷的电离能为0.04eV，求室温下杂质一般电离时费米能级的位置和磷的浓度。

(7)3－19．（P82）求室温下掺锑的n型硅，使EF＝(EC＋ED)/2时的锑的浓度。

已知锑的电离能为0.039eV。

(7)3－20．（P82）制造晶体管一般是在高杂质浓度的n型衬底上外延一层n型的外延层，再在外延层中扩散硼、磷而成。

①设n型硅单晶衬底是掺锑的，锑的电离能为0.039eV，300k时的EF位于导带底下面0.026eV处，计算锑的浓度和导带中电子浓度。

(8)4－1．（P113）300K时，Ge的本征电阻率为47Ω.cm，如电子和空穴迁移率分别为3900cm2/V.S和1900cm2/V.S，试求本征Ge的载流子浓度。

第一章习题1.晶体与非晶体最本质的区别是什么?准晶体是一种什么物态?答：晶体和非晶体均为固体，但它们之间有着本质的区别。

晶体是具有格子构造的固体，即晶体的内部质点在三维空间做周期性重复排列。

而非晶体不具有格子构造。

晶体具有远程规律和近程规律，非晶体只有近程规律。

准晶态也不具有格子构造，即内部质点也没有平移周期，但其内部质点排列具有远程规律。

因此，这种物态介于晶体和非晶体之间。

2.在某一晶体结构中，同种质点都是相当点吗?为什么?答：晶体结构中的同种质点并不一定都是相当点。

因为相当点是满足以下两个条件的点：a.点的内容相同；b.点的周围环境相同。

同种质点只满足了第一个条件，并不一定能够满足第二个条件。

因此，晶体结构中的同种质点并不一定都是相当点。

3.从格子构造观点出发，说明晶体的基本性质。

答：晶体具有六个宏观的基本性质，这些性质是受其微观世界特点，即格子构造所决定的。

现分别叙述：a.自限性晶体的多面体外形是其格子构造在外形上的直接反映。

晶面、晶棱与角顶分别与格子构造中的面网、行列和结点相对应。

从而导致了晶体在适当的条件下往往自发地形成几何多面体外形的性质。

b.均一性因为晶体是具有格子构造的固体，在同一晶体的各个不同部分，化学成分与晶体结构都是相同的，所以晶体的各个部分的物理性质与化学性质也是相同的。

c.异向性同一晶体中，由于内部质点在不同方向上的排布一般是不同的。

因此，晶体的性质也随方向的不同有所差异。

d.对称性晶体的格子构造本身就是质点周期性重复排列，这本身就是一种对称性；体现在宏观上就是晶体相同的外形和物理性质在不同的方向上能够有规律地重复出现。

e.最小内能性晶体的格子构造使得其内部质点的排布是质点间引力和斥力达到平衡的结果。

无论质点间的距离增大或缩小，都将导致质点的相对势能增加。

因此，在相同的温度条件下，晶体比非晶体的内能要小；相对于气体和液体来说，晶体的内能更小。

f.稳定性内能越小越稳定，晶体的稳定性是最小内能性的必然结果。

第五章 晶格振动习题和答案1．什么叫简正振动模式？简正振动数目、格波数目或格波振动模式数目是否是一回事？[解答] 为了使问题既简化又能抓住主要矛盾，在分析讨论晶格振动时，将原子间互作用力的泰勒级数中的非线性项忽略掉的近似称为间谐近似。

在间谐近似下，由N 个原子构成的晶体的晶格振动，可等效成3N 个独立的谐振子的振动。

每个谐振子的振动模式称为间正振动模式，它对应着所有的原子都以该模式的频率做振动，它是晶格振动模式中最简单最基本的振动方式。

原子的振动，或者说格波振动通常是这3N 个简正振动模式的线性迭加。

简正振动数目、格波数目或格波振动模式数目是一回事，这个数目等于晶体中所有原子的自由度数之和，即等3N 。

2．长光学支格波与长声学支格波本质上有何差别？[解答] 长光学支格波的特征是每个原胞内的不同原子做相对振动，振动频略较高，它包含了晶格振动频率最高的振动模式。

长声学支格波的特征原胞内的不同原子没有相对位移，原胞做整体运动，振动频率较低，它包含了晶格振动频率最低的振动模式，波速是一常数。

任何晶体都存在声学支格波，但简单晶格（非复式格子）晶体不存在光学支格波。

3． 温度一定，一个光学波的声子数目多呢，还是声学波的声子数目多？ [解答] 频率为ω的格波的（平均）声子数为11)(/-=T k B e n ωω因为光学波的频率0ω比声学波的频率A ω高，（1/0-Tk B eω ）大于（1/-T k B A e ω ），所以在温度一定情况下，一个光学波的声子数目少于一个声学波的声子数目。

4． 对同一个振动模式，温度高时的声子数目多呢，还是温度低时的声子数目多呢？[解答] 设温度H T 〉L T ，由于（1/-HB T k eω ）大于（1/-L B T k e ω ），所以对同一个振动模式，温度高时的声子数目多于温度低时的声子数目。

5． 高温时，频率为ω的格波的声子数目与温度有何关系？[解答] 温度很高时，T k eB Tk B /1/ωω +≈ ，频率为ω的格波的（平均）声子数为ωωω Tk e n B T k B ≈-=11)(/ 可见高温时，格波的声子数目与温度近似成正比。

方一陆固物习题参考答案1、布格子：每个原胞内只有一个原子的晶格或组成晶体结构的基元之结点：如以Cl 原子为结点，取面心立方晶胞，就是NaCl 的布氏格子；金刚石结构中位于正四面体中心的原子和顶角上的原子化学组份虽相同，但电子云配置方位不同，所以是复式格子。

2、如以321,,→→→a a a 为正格子基矢则满足。

当相应的同理得则得相应格点则得当令法线上确定一长度在面间距为则对应晶石的所决定之晶石矢标面为正晶格内原胞基座含晶格之倒格子确定的格子叫的或Ω⨯=Ω⨯=±±=Ω⨯===⨯⋅=Ω=Ω⨯=Ω⨯=⋅=⋅→→→→→→→→→→→→→→→→→→→→→→→→→→→→→313132321213212132132132131323212;2,2,12,10,2,,,,,,,,)(,2,22a a b a a b a a b d a a d a a a a a a a b b b a a a b a a b a a b a a ij j i ππμπμπμρρπππδ.,,,,2,1321个倒格点集合即得整原胞在倒易空间中平移即相当于以时→→→±±=b b b μ3、体心立方格子和面心立方格子互为正倒格子，试证明之。

设体心立方格子的结晶学晶胞（Convention cell ）的基矢是,,11→→→c b a 令→→→k j ,,i 为直角坐标的三个互垂直的单位矢a k c a jb a i a →→→→→===,,这个体心立方格子的固体物理学原胞（Primitive cell ）的三个基矢，按规定)(2),(2),(2321→→→→→→→→→→→→++=--=++-=k j a a k j a a k j a a λλλ的三个基矢理学原胞它们是倒点阵的固体物定义cell)(Primitive )(2)(2)(2)(221,2:321232332132321⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+=+=+=+=⨯=⨯⋅=Ω==Ω⨯=→→→→→→→→→→→→→→→→→→→→→j i a b i k a b k j ab k j a a a a a a a b b a a b ππππ这个倒点阵的结晶学胞原（Convention cell ）应当是显示其立方晶系对称性的最小重复单元。

2023年固体物理基础第三版（阎守胜著）课后题答案下载固体物理基础第三版（阎守胜著）课后答案下载第一章金属自由电子气体模型1.1 模型及基态性质1.1.1 单电子本征态和本征能量1.1.2 基态和基态的能量1.2 自由电子气体的热性质1.2.1 化学势随温度的变化1.2.2 电子比热1.3 泡利顺磁性1.4 电场中的`自由电子1.4.1 准经典模型1.4.2 电子的动力学方程1.4.3 金属的电导率1.5 光学性质1.6 霍尔效应和磁阻1.7 金属的热导率1.8 自由电子气体模型的局限性第二章晶体的结构2.1 晶格2.1.1 布拉维格子2.1.2 原胞2.1.3 配位数2.1.4 几个常见的布拉维格子2.1.5 晶向、晶面和基元的坐标2.2 对称性和布拉维格子的分类2.2.1 点群2.2.2 7个晶系2.2.3 空间群和14个布拉维格子2.2.4 单胞或惯用单胞2.2.5 二维情形2.2.6 点群对称性和晶体的物理性质 2.3 几种常见的晶体结构2.3.1 CsCl结构和立方钙钛矿结构 2.3.2 NaCl和CaF、2结构2.3.3 金刚石和闪锌矿结构2.3.4 六角密堆积结构2.3.5 实例，正交相YBa2Cu307-82.3.6 简单晶格和复式晶格2.4 倒格子2.4.1 概念的引入2.4.2 倒格子是倒易空间中的布拉维格子 2.4.3 倒格矢与晶面2.4.4 倒格子的点群对称性2.5 晶体结构的实验确定2.5.1 X射线衍射2.5.2 电子衍射和中子衍射2.5.3 扫描隧穿显微镜第三章能带论I3.1 布洛赫定理及能带3.1.1 布洛赫定理及证明3.1.2 波矢七的取值与物理意义3.1.3 能带及其图示3.2 弱周期势近似3.2.1 一维情形3.2.2 能隙和布拉格反射3.2.3 复式晶格3.3 紧束缚近似3.3.1 模型及计算3.3.2 万尼尔函数3.4 能带结构的计算3.4.1 近似方法3.4.2 n(K)的对称性3.4.3 n(K)和n的图示3.5 费米面和态密度3.5.1 高布里渊区3.5.2 费米面的构造3.5.3 态密度第四章能带论Ⅱ4.1 电子运动的半经典模型 4.1.1 模型的表述4.1.2 模型合理性的说明4.1.3 有效质量4.1.4 半经典模型的适用范围4.2 恒定电场、磁场作用下电子的运动4.2.1 恒定电场作用下的电子4.2.2 满带不导电4.2.3 近满带中的空穴4.2.4 导体、半导体和绝缘体的能带论解释 4.2.5 恒定磁场作用下电子的准经典运动 4.3 费米面的测量4.3.1 均匀磁场中的自由电子4.3.2 布洛赫电子的轨道量子化4.3.3 德哈斯一范阿尔芬效应4.3.4 回旋共振方法4.4 用光电子谱研究能带结构4.4.1 态密度分布曲线4.4.2 角分辨光电子谱测定n(K)4.5 一些金属元素的能带结构4.5.1 简单金属4.5.2 一价贵金属4.5.3 四价金属和半金属4.5.4 过渡族金属和稀土金属第五章晶格振动5.1 简谐晶体的经典运动5.1.1 简谐近似5.1.2 一维单原子链，声学支 5.1.3 一维双原子链，光学支 5.1.4 三维情形5.2 简谐晶体的量子理论5.2.1 简正坐标5.2.2 声子5.2.3 晶格比热5.2.4 声子态密度5.3 晶格振动谱的实验测定 5.3.1 中子的非弹性散射5.3.2 可见光的非弹性散射 5.4 非简谐效应5.4.1 热膨胀5.4.2 晶格热导率第六章输运现象6.1 玻尔兹曼方程6.2 电导率6.2.1 金属的直流电导率6.2.2 电子和声子的相互作用 6.2.3 电阻率随温度的变化 6.2.4 剩余电阻率6.2.5 近藤效应06.2.6 半导体的电导率6.3 热导率和热电势6.3.1 热导率6.3.2 热电势6.4 霍尔系数和磁阻第七章固体中的原子键合7.1 概述7.1.1 化学键7.1.2 晶体的分类7.1.3 晶体的结合能7.2 共价晶体7.3 离子晶体7.3.1 结合能7.3.2 离子半径7.3.3 部分离子部分共价的晶体7.4 分子晶体、金属及氢键晶体7.4.1 分子晶体7.4.2 量子晶体7.4.3 金属……第八章缺陷第九章无序第十章尺寸第十一章维度第十二章关联固体物理基础第三版（阎守胜著）：基本信息阎守胜，1938生出生，1962年毕业于北京大学物理系，现任北京大学物理学院教授，博士生导师，兼任中国物理学会《物理》杂志主编，他长期从事低温物理，低温物理实验技术，高温超导电性物理和介观物理方面的实验研究，并讲授大学生的固体物理学，低温物理学和现代固体物理学等课程。