高等数学上学期期末考试试题和答案解析四份上课讲义

高等数学试卷（B 卷）答案及评分标准2004-2005年度第一学期科目:高等数学I 班级:姓名:学号:成绩: 一、填空题（5153'=⨯'）1、()3)2ln(--=x x x f 的定义域是_2、 2 )1sin 2sin (lim 0x =⋅+→xx x x 3、 e )31(lim 3=+∞→xx x4、如果函数x x a x f 3sin 31sin )(+=，在3π=x 处有极值，则2=a5、34d )1(sin cos 223=+⋅⎰-x x x ππ二、单项选择题（5153'=⨯'）1、当0→x 时，下列变量中与2x 等价的无穷小量是（）A.x cos 1-B.2x x +C.1-x eD.x x sin )ln(1+2、)A ()(' ,)(的是则下列极限中等于处可导在设a f a x x f =。

A ．h h a f a f h )()(lim0--→B ．hh a f h a f h )()(lim 0--+→C ．h a f h a f h )()2(lim 0-+→D ．h h a f h a f h 3)()2(lim 0--+→3、设在[]b a ,上函数)(x f 满足条件()0)(,0<''>'x f x f 则曲线()x f y =在该区间上（） A.上升且凹的B.上升且凸的C.下降且凹的D.下降且凸的4、设函数()x f 具有连续的导数，则以下等式中错误的是（）A.)(d )(d d x f x x f x b a =⎪⎭⎫ ⎝⎛⎰ B.x x f t t f x a d )(d )(d =⎪⎭⎫ ⎝⎛⎰ C.()x x f x x f d )(d )(d=⎰ D.C t f t t f +='⎰)(d )(5、反常积分⎰∞+- 0d 2x xe x （）A.发散B.收敛于1C.收敛于21D.收敛于21-三、算题（'488'6=⨯）1、求极限xxx x 30sin sin tan lim -→2、求22)2()ln(sin lim x x x -→ππ3、求曲线⎩⎨⎧==ty tx 2cos sin 在当4π=t 处的切线方程和法线方程4、已知函数0,sin >=x x y x ，计算xy d d5、求积分⎰x e xd6、求积分x x e ed ln 1⎰7、计算曲线π≤≤=x x y 0,sin 与x 轴围成的图形面积，并求该图形绕y 轴所产生的旋转体体积。

第一学期期末高等数学试卷一、解答下列各题(本大题共16小题，总计80分) 1、(本小题5分)求极限　lim x x x x x x →-+-+-23321216291242、(本小题5分).d )1(22x x x⎰+求3、(本小题5分)求极限lim arctan arcsinx x x →∞⋅14、(本小题5分)⎰-.d 1x x x 求5、(本小题5分)．求dt t dx d x ⎰+2021 6、(本小题5分)⎰⋅.d csc cot 46x x x 求7、(本小题5分)．求⎰ππ2121cos 1dx x x8、(本小题5分)设确定了函数求．x e t y e t y y x dy dx t t==⎧⎨⎪⎩⎪=cos sin (),229、(本小题5分)．求dx x x ⎰+3110、(本小题5分)求函数　的单调区间y x x =+-422 11、(本小题5分)．求⎰π+202sin 8sin dx x x12、(本小题5分)．，求设　dx t t e t x kt )sin 4cos 3()(ωω+=- 13、(本小题5分)设函数由方程所确定求．y y x y y x dy dx =+=()ln ,22614、(本小题5分)求函数的极值y e e x x =+-2 15、(本小题5分)求极限lim()()()()()()x x x x x x x →∞++++++++--12131101101111222216、(本小题5分).d cos sin 12cos x x x x⎰+求二、解答下列各题(本大题共2小题，总计14分) 1、(本小题7分),,512沿一边可用原来的石条围平方米的矩形的晒谷场某农场需建一个面积为.,,才能使材料最省多少时问晒谷场的长和宽各为另三边需砌新石条围沿2、(本小题7分).8232体积轴旋转所得的旋转体的所围成的平面图形绕和求由曲线ox x y x y ==三、解答下列各题 ( 本 大 题6分 )设证明有且仅有三个实根f x x x x x f x ()()()(),().=---'=1230一学期期末高数考试(答案)一、解答下列各题(本大题共16小题，总计77分) 1、(本小题3分)解原式:lim =--+→x x x x 22231261812 =-→limx xx 261218 =2 2、(本小题3分)⎰+xx xd )1(22⎰++=222)1()1d(21x x =-++12112x c .3、(本小题3分)因为arctan x <π2而lim arcsin x x →∞=1故lim arctan arcsin x x x →∞⋅=14、(本小题3分)⎰-x x xd 1xx x d 111⎰----=⎰⎰-+-=x xx 1d d=---+x x c ln .1 5、(本小题3分)原式=+214x x6、(本小题4分)⎰⋅x x x d csc cot 46⎰+-=)d(cot )cot 1(cot 26x x x=--+171979cot cot .x x c7、(本小题4分)原式=-⎰cos ()1112x d x ππ=-sin112xππ=-1 8、(本小题4分)解： dy dx e t t e t t t t t =+-22222(sin cos )(cos sin ) =+-e t t t t t t (sin cos )(cos sin )22229、(本小题4分)令　1+=x u原式=-⎰24122()u u du=-2535312()u u =11615 10、(本小题5分)),(+∞-∞函数定义域 01)1(222='=-=-='y x x x y ，当(][)+∞<'>∞->'<,1011,01函数的单调减区间为，当函数单调增区间为，　当y x y x 11、(本小题5分)原式=--⎰d x x cos cos 9202π=-+-163302lncos cos x x π=162ln 12、(本小题6分)dx x t dt ='()[]dt t k t k e kt ωωωωsin )34(cos )34(+--=-　13、(本小题6分)2265yy y y x '+'='=+y yx y 315214、(本小题6分)定义域，且连续(),-∞+∞'=--y e e x x 2122()驻点：x =1212ln由于''=+>-y e e x x 2022)21ln 21(,,=y 故函数有极小值15、(本小题8分)原式=++++++++--→∞lim()()()()()()x x x x x x x 112131*********2222=⨯⨯⨯⨯=1011216101172 16、(本小题10分)dxxxdx x x x ⎰⎰+=+2sin 2112cos cos sin 12cos :解⎰++=xx d 2sin 211)12sin 21( =++ln sin 1122x c二、解答下列各题(本大题共2小题，总计13分) 1、(本小题5分)设晒谷场宽为则长为米新砌石条围沿的总长为 x xL x x x ,,()51225120=+> '=-=L x x 2512162 唯一驻点 ''=>=L x x 10240163 即为极小值点故晒谷场宽为米长为米时可使新砌石条围沿所用材料最省165121632,,=(完整word 版)大一第一学期期末高等数学(上)试题及答案2、(本小题8分)解 :,,.x x x x x x 232311288204====V x x dx x x dxx =-⎡⎣⎢⎤⎦⎥=-⎰⎰ππ()()()223204460428464=⋅-⋅π()1415164175704x x π=-π=35512)7151(44三、解答下列各题 ( 本 大 题10分 )证明在连续可导从而在连续可导:()(,),,[,];,.f x -∞+∞03 又f f f f ()()()()01230====则分别在上对应用罗尔定理得至少存在[,],[,],[,](),011223f x ξξξξξξ1231230112230∈∈∈'='='=(,),(,),(,)()()()使f f f 即至少有三个实根'=f x (),0,,,0)(它至多有三个实根是三次方程又='x f由上述有且仅有三个实根'f x ()高等数学（上）试题及答案一、 填空题（每小题3分，本题共15分）1、.______)31(lim 2=+→xx x 。

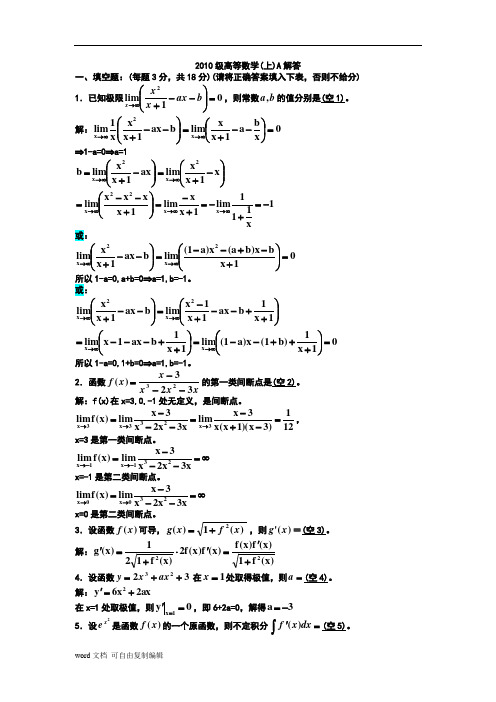
2010级高等数学(上)A 解答一、填空题：(每题3分，共18分)(请将正确答案填入下表，否则不给分)1．已知极限01lim 2=⎪⎪⎭⎫⎝⎛--+∞→b ax x x x ，则常数b a ,的值分别是(空1)。

解：0x b a 1x x lim b ax 1x x x 1lim x 2x =⎪⎭⎫ ⎝⎛--+=⎪⎪⎭⎫ ⎝⎛--+∞→∞→ ⇒1-a=0⇒a=1⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=∞→∞→x 1x x lim ax 1x x lim b 2x 2x 1x111lim 1x x lim 1x x x x lim x x 22x -=+-=+-=⎪⎪⎭⎫ ⎝⎛+--=∞→∞→∞→ 或：01x b x )b a (x )a 1(lim b ax 1x x lim 2x 2x =⎪⎪⎭⎫⎝⎛+-+--=⎪⎪⎭⎫ ⎝⎛--+∞→∞→ 所以1-a=0,a+b=0⇒a=1,b=-1。

或：⎪⎪⎭⎫⎝⎛++--+-=⎪⎪⎭⎫ ⎝⎛--+∞→∞→1x 1b ax 1x 1x lim b ax 1x x lim 2x 2x 01x 1)b 1(x )a 1(lim 1x 1b ax 1x lim x x =⎪⎭⎫ ⎝⎛+++--=⎪⎭⎫ ⎝⎛++---=∞→∞→ 所以1-a=0,1+b=0⇒a=1,b=-1。

2．函数xx x x x f 323)(23---=的第一类间断点是(空2)。

解：f(x)在x=3,0,-1处无定义，是间断点。

121)3x )(1x (x 3x lim x 3x 2x 3x lim)x (f lim 3x 233x 3x =-+-=---=→→→，x=3是第一类间断点。

∞=---=-→-→x3x 2x 3x lim)x (f lim 231x 1xx=-1是第二类间断点。

∞=---=→→x3x 2x 3x lim)x (f lim 230x 0xx=0是第二类间断点。

3．设函数)(x f 可导，)(1)(2x f x g +=，则)('x g ＝(空3)。

高数(大一上)期末试题及答案第一学期期末考试试卷（1）课程名称：高等数学（上）考试方式：闭卷完成时限：120分钟班级：学号：姓名：得分：一、填空（每小题3分，满分15分）1.lim (3x^2+5)/ (5x+3x^2) = 02.设 f''(-1) = A，则 lim (f'(-1+h) - f'(-1))/h = A3.曲线 y = 2e^(2t) - t 在 t = 0 处切线方程的斜率为 44.已知 f(x) 连续可导，且 f(x)。

0，f(0) = 1，f(1) = e，f(2) = e，∫f(2x)dx = 1/2ex，则 f'(0) = 1/25.已知 f(x) = (1+x^2)/(1+x)，则 f'(0) = 1二、单项选择（每小题3分，满分15分）1.函数 f(x) = x*sinx，则 B 选项为正确答案，即当x → ±∞ 时有极限。

2.已知 f(x) = { e^x。

x < 1.ln x。

x ≥ 1 }，则 f(x) 在 x = 1 处的导数不存在，答案为 D。

3.曲线 y = xe^(-x^2) 的拐点是 (1/e。

1/(2e))，答案为 C。

4.下列广义积分中发散的是 A 选项，即∫dx/(x^2+x+1)在区间 (-∞。

+∞) 内发散。

5.若 f(x) 与 g(x) 在 (-∞。

+∞) 内可导，且 f(x) < g(x)，则必有 B 选项成立，即 f'(x) < g'(x)。

三、计算题（每小题7分，共56分）1.lim x^2(e^(2x)-e^(-x))/((1-cosx)sinx)lim x^2(e^(2x)-e^(-x))/((1-cosx)/x)*x*cosxlim x(e^(2x)-e^(-x))/(sinx/x)*cosxlim (2e^(2x)+e^(-x))/(cosx/x)应用洛必达法则)2.lim {arcsin(x+1) + arcsin(x-1) - 2arcsin(x)}/xlim {arcsin[(x+1)/√(1+(x+1)^2)] + arcsin[(x-1)/√(1+(x-1)^2)] - 2arcsin(x)/√(1+x^2)}lim {arcsin[(x+1)/√(1+(x+1)^2)] - arcsin(x/√(1+x^2)) + arcsin[(x-1)/√(1+(x-1)^2)] - arcsin(x/√(1+x^2))}lim {arcsin[(x+1)/√(1+(x+1)^2)] - arcsin(x/√(1+(x+1)^2)) + arcsin[(x-1)/√(1+(x-1)^2)] - arcsin(x/√(1+(x-1)^2))}lim {arcsin[(x+1)/√(1+(x+1)^2)] - arcsin[(x-1)/√(1+(x-1)^2)]} π/2 (应用洛必达法则)3.y = y(x) 由 x + y - 3 = 0 确定，即 y = 3 - x，因此 dy/dx = -1.4.f(x) = arctan(2x-9) - arctan(x-3) 的导数为 f'(x) = 1/[(2x-9)^2+1] - 1/[(x-3)^2+1]，因此 f'(x)。

一、填空题(每小题2分，共20分)1. 0，2.21，3. t −，4. 4，5. )41 0(]41 0[，或，，6. (0, 2)， 6. C x x ++arctan 3)1(分给缺C ，8. 0，9. 34−，10. 23.二、试解下列各题(每小题6分，共24分)1. xx x x x x 4sin 3553lim 22++=∞→原式 2分 444sin 3553lim20⋅⋅++=→xx x x x 4分 5124153=⋅⋅=6分 2. )1(sin )]1sin(sin ['⋅−='xx y 2分)1(1cos )]1sin(sin ['⋅−=xx x 3分x x x 1cos )1sin(sin 12=4分dx x x x dx y dy 1cos )1sin(sin 12='= 6分3. x x x d )111(22+−=⎰原式 1分 dx x dx x dx x ⎰⎰⎰+−++=21)1111(21 3分 .111ln 21C xx x +−−+= 6分 dx xx⎰+=422cos 2cos 1 4.π原式 2分⎰+=42)1(sec 21πdx x 3分40)(tan 21πx x += 5分 821π+= 6分三、试解下列各题(每小题7分，共28分)42021lim 1.x e x x x −→−−=原式 2分30422lim 2x xe x x x −→+−= 4分 22012422lim 22x e x e x x x −−→−+−= 5分x e x xe x x x 24812lim 2230−−→+−= 6分21−= 7分)(02/1 4422x x x e x ++−=−或用泰勒公式3分， 答案2分2. )(x df x ⎰=原式 1分dx x f x xf ⎰−=)()( 3分C xxx x x +−'=ln )ln ( 5分 C xx+−=ln 21 7分 分给求出注：2 ln 1)ln ()( xxx x x f −='= 1 2 1 0 1 3.==−====−t x t x dt dx t x 时，，时，且，则，令 1分 dt t f ⎰−=11 )(原式 2分dt tdt e t ⎰⎰+++=−1 0 01 11 114分 1001)1ln()]1ln([t e t t +++−=− 6分)1ln(e += 7分⎪⎩⎪⎨⎧<+≥=−−1 111 1)1(1x e x x x f x ，，或 2分 dx xdx e x ⎰⎰−+=2 1 10 1111＋原式 4分下面同上}2 1 2{ }1 1 1{ 4.21−=−=，，，，，两平面的法向量为n n 1分所求直线的方向向量2111−−=kj s 2分}3 4 1{，，= 4分334112−=+=−z y x 对称式方程为6分 ⎪⎩⎪⎨⎧+=+−=+= 3341 2t z t y t x 参数方程为 7分四、应用题(每小题7，共21分)分 其体积为　则圆柱体的底面半径，设内接圆柱体的高为3 20)4()2( 1.2222R h h R h V hR r h <<−=−=π分4 )43(22h R V −='πR h V 3320=='得：唯一驻点　令 5分 023<−=''h V π又，圆柱体体积最大时故当,332R h = 7分dx x x dx x x V ⎰⎰−+−=2422422)cos (sin )sin (cos 2.πππππ3分dx x dx x ⎰⎰−=2442cos 2cos πππππ4分2442sin 22sin 2πππππxx−=5分π= 7分)1(3d 3.12 C x x y y +=''='⎰1分232632−==−x y y x 得又由 2分 得 代入)1(32)2,0(='∴−y 3分 '=+y x 332 4分23232d )323(C x x x x y ++=+=∴⎰5分.2322)2,0(31−+=∴−=−x x y C ，代入得再将 7分。

第一学期期末高等数学试卷一、解答以下各题(本大题共16小题，总计 80分) 1、(本小题5分)求极限l imx 312x 163 9x 212x4x 22x 2、(本小题5 分)求x 2dx.(1 2 )x3、(本小题5 分)求极限limarctanx arcsin 1xx 4、(本小题5 分)求x dx. 1x5、(本小题5 分)求ddxx 21t 2dt ．6、(本小题5分) 求cot 6xcsc 4xdx.7、(本小题5分)21 cos 1dx ．求1 x 2 x8、(本小题5 分)x e t cost 2y(x),求dy．设确定了函数yy e 2t sintdx9、(本小题5 分)3求 x1xdx ．10、(本小题5分)求函数 y 4 2x x 2的单调区间 11、(本小题5分)求2sinx dx ．sin 2x0812、(本小题 5 分)设xt ) e kt(3cos t4sint ，求dx ．()13、(本小题 5 分)设函数yyx 由方程y 2ln y 2x 6所确定 , 求dy ．( )dx14、(本小题 5 分)求函数yexe x的极值215、(本小题 5 分)求极限lim(x1)2 (2x1)2 (3x1)2(10x 1)2x16、(本小题5分)(10x 1)(11x 1)求cos2x dx. sinxcosx 1二、解答以下各题(本大题共2小题，总计14分)第1页，共8页1、(本小题7分)某农场需建一个面积为512平方米的矩形的晒谷场,一边可用原来的石条围沿,另三边需砌新石条围沿,问晒谷场的长和宽各为多少时,才能使材料最省.2、(本小题7分)求由曲线yx 2 和y x 3 所围成的平面图形绕 ox 轴旋转所得的旋转体的 体积.28三、解答以下各题 (本大题6分)设f(x) x(x 1)(x 2)(x3),证明f(x) 0有且仅有三个实根.一学期期末高数考试(答案)一、解答以下各题 (本大题共16小题，总计77分)1、(本小题3分)解:原式lim 3x 2 12218x12x26x6xlim212x1822、(本小题3分)dx (1x 2)21d(1 x 2) 12(1x 2)211x 2c.3、(本小题3分)因为arctanx2而limarcsinx故limarctanxarcsin1xx4、(本小题3分)x dx1 x1 x 1dx 1xdxdx1xxln1xc.5、(本小题3分) 原式2x1x 4 6、(本小题4分) cot 6xcsc 4xdxcot 6x(1cot 2x)d(cotx)1x第2页，共8页1cot 7x1cot 9 xc. 797、(本小题 4分)21 1原式1cos d( )xx1 sinx2118、(本小题4 分)解：dy e 2t (2sint cost) dxe t(cost22tsint 2) e t (2sintcost)(cost 22tsint 2)9、(本小题4 分)令 1xu2原式2 (u 4u 2)du12(u 5u 3 )12 531161510、(本小题5分)函数定义域(, )y22x2(1 x)当x1，y0当x ，y函数单调增区间为 ,11当x， y函数的单调减区间为1,1 011、(本小题 5分)原式2 dcosx9 cos 2x1 3 cosx 2lncosx 06 31ln2612、(本小题 6分)dxx(t)dte kt(43k)cost(4k3)sintdt13、(本小题 6分)2yy2y 6x 5yy 3yx 5y2114、(本小题 6分)y定义域( ， ),且连续 2e x(e2x1) 2第3页，共8页驻点：x1ln 12 2由于y2e x e x故函数有极小值,,y(1ln1) 2 215、(本小题 8分) 22(1 1 )2 (2 1 )2 (3 1 )2(10 1 )2原式lim x xxxx (10 1)(11 1)10 11 21x x6 10 117216、(本小题 10分)解:cos2x dxcos2x dx1 sinxcosx11sin2xd(12sin2x 1)2 11sin2x12sin2xcln12二、解答以下各题(本大题共2小题，总计13 分)1、(本小题5 分)设晒谷场宽为 x,那么长为512米,新砌石条围沿的总长为xL2x 512 (x0)xL2512唯一驻点x16x 2L1024 0即x16为极小值点x 3故晒谷场宽为 16米,长为51232米时,可使新砌石条围沿16所用材料最省2、(本小题8分)解:x 2 x 3, 22x 3 x 1,.28x0x 148V x4 x 2 )2( x 32 dx 4x4x 6( ) 0()dx28464(11x 5 41 1x 7)4 564 744(11) 512三、解答以下各题 5735(本大题10分)证明:f(x)在(, )连续,可导,从而在[0,3];连续,可导.第4页，共8页又f(0)f(1)f(2)f(3)0那么分别在[0,1],[1,2],[2,3]上对f(x)应用罗尔定理得,至少存在1(0,1),2(1,2),3(2,3)使f(1)f(2)f(3)0即f(x)0至少有三个实根,又f(x)0,是三次方程,它至多有三个实根,由上述f(x)有且仅有三个实根高等数学〔上〕试题及答案一、填空题〔每题3分，此题共15分〕21、lim(13x)x______.。

1、 (本小题 5 分 )求极限limx 3 12 x1639x 212x 4x 22x2、(本小题 5 分)求x2 2dx. (1 x )3、(本小题 5 分)求极限 limarctan x arcsin1xx4、 (本小题 5 分 )求xd x.1 x5、 (本小题 5 分 )求dx 21 t2 dt ．dx6、(本小题 5 分)求 cot 6 x csc 4 x d x.第 1页，共 10页（第七题删掉了）8、 (本小题 5 分 )设xe t cost 2确立了函数 y y( x), 求dy．ye 2t sin tdx9、(本小题 5 分)3求 x 1x dx ．10、 (本小题 5 分 )求函数y 4 2 x x 2 的单一区间11、 (本小题 5 分 )求 2sin x．8sin 2 dxx12、 (本小题 5 分 )设 x t )e kt(3cost4 sin t ，求 dx ．()13、 (本小题 5 分 )设函数 y y x 由方程 y 2ln y 2x 6 所确立 , 求 dy ．( )dx14、 (本小题 5 分 )求函数 y2e x e x 的极值第 2页，共 10页15、 (本小题 5 分 )求极限lim ( x 1)2(2x 1)2( 3x 1) 2(10x 1)2x(10x 1)(11x1)16、 (本小题 5 分 )求cos2x d x.1sin xcos x二、解答以下各题(本大题共 2 小题，总计14 分 )1、(本小题 7 分)某农场需建一个面积为 512平方米的矩形的晒谷场 ,一边可用本来的石条围沿,另三边需砌新石条围沿 ,问晒谷场的长和宽各为多少时 ,才能使资料最省 .2、 (本小题 7分 )求由曲线 y x 2和 y x 3所围成的平面图形绕ox轴旋转所得的旋转体的体积 .28三、解答以下各题(本大题6分)设 f (x) x(x 1)( x 2)( x 3), 证明 f ( x) 0有且仅有三个实根.(答案)一、解答以下各题(本大题共 16 小题，总计77 分 )1、(本小题 3 分)第 3页，共 10页解:原式lim 3x 2 12218x 12x 2 6x6xlimx 212 x 1822、(本小题 3 分)x d x(1 x 2 ) 21 d(1 x2 )2(1x 2 ) 2112 1 x 2c.3、(本小题 3 分)因为 arctan x2而 limarcsin 1xx故 limarctan x arcsin1xx4、(本小题 3 分)xd x1 x1 x 1 d x 1 xd xd x1 xx ln 1 x c.5、(本小题 3 分)求 ddx x 21 t2 dt ．原式2 x 1 x 46、 (本小题 4 分 )cot 6 x csc 4 x d xcot 6 x(1 cot 2 x) d(cot x)1 cot 7 x 1 cot 9 x c.7 98、 (本小题 4 分 )xe t cost 2y( x), 求 dy．设确立了函数 yye 2 t sin tdx解：dy e 2t (2 sin t cost)dxe t(cos t22t sin t 2)e t (2 sin t cost)(cost 2 2t sin t 2 )9、 (本小题 4 分 )3求 x 1 x dx ．令 1 xu2 原式2 (u 4u 2 ) du1第 4页，共 10页2( u 5 u 3 ) 12 5 3 1161510、 (本小题 5 分 )求函数y4 2 x x 2 的单一区间解： 函数定义域 ( , )y 2 2 x 2(1 x)当 x 1， y 0当x ， y函数单一增区间为,11当x， y函数的单一减区间为1,1 011、 (本小题 5 分 )求 2sin x ．8 sin 2 dxx原式2 d cos x9 cos 2x13 cosx 2lncosx 0631l n 2612、 (本小题 6 分 )设 x t ) e kt(3cos t 4 sin t ，求 dx ．()解：dxx ( t) dte kt(4 3k ) cos t ( 4k 3) sin t dt13、 (本小题 6 分 )设函数 yy x 由方程 y 2ln y 2x 6 所确立, 求 dy ．( )dx2y2yy6x 5y53yx14、 (本小题 6 分 )求函数 y2e xe x 的极值解：定义域 (，), 且连续y 2e x (e2 x1) 2驻点： x1 ln 12 2因为 y2e xe x故函数有极小值 ,, y( 1 ln 1 ) 2 215、 (本小题 8 分 )2 2求极限 lim( x 1)2(2x 1)2 ( 3x 1) 2(10x 1)2x(10x 1)(11x 1)第 5页，共 10页(1 1) 2 ( 2 1 )2 ( 3 1) 2(10 1 ) 2原式limx x xx11x)(11 )(10 xx10 11 21 6 10 11 7 216、 (本小题 10 分 )解 :cos2x dxcos2x dx1 sin x cos x1 1 sin 2x2d( 1sin 2x1)2112 sin 2xln 11sin 2x c2二、解答以下各题(本大题共 2 小题，总计 13 分 )1、(本小题 5 分)某农场需建一个面积为 512平方米的矩形的晒谷场 ,一边可用本来的石条围 沿,另三边需砌新石条围沿 ,问晒谷场的长和宽各为 多少时 ,才能使资料最省 .设晒谷场宽为 x, 则长为512米 ,新砌石条围沿的总长为x L2x512(x0)xL2512 独一驻点x 16x 2L1024 0 即 x 16 为极小值点x 3故晒谷场宽为 16米 , 长为51232米时 , 可使新砌石条围沿16所用资料最省2、 (本小题 8 分 )求由曲线 yx 2 和 y x 3 所围成的平面图形绕 ox 轴旋转所得的旋转体的体积 .2 8解:x 2x 3 , 22x3x 1,.28x0 x 148V x4 x 2)2 (x 3 2 dx4 x 4x 6() 0()dx28464(11 x 541 1 x 7 )4 564 744 ( 11 ) 51257 35三、解答以下各题 (本大题10分)设 f (x) x(x 1)( x 2)( x 3), 证明 f ( x) 0有且仅有三个实根 .第 6页，共 10页证明 : f (x)在 (,) 连续 , 可导 , 进而在 [ 0,3]; 连续 , 可导 .又 f (0) f (1) f (2) f (3)0则分别在 [0,1],[ 1,2],[ 2,3] 上对 f ( x) 应用罗尔定理得, 起码存在1(0,1),2(1,2),3(2,3)使 f ( 1 ) f ( 2 ) f ( 3 )0即 f (x) 0起码有三个实根 , 又f (x) 0,是三次方程,它至多有三个实根,由上述 f ( x) 有且仅有三个实根一、填空题（每题 3 分，此题共15 分）21、lim (13x) x______ . 。

高三数学上册期末试卷及答案解析高三数学上册期末试卷及答案解析一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合M={0，1，2，3，4}，N={x|1A.{1}B.{2，3}C.{0，1}D.{2，3，4}2.已知a R，则 |a﹣1|+|a| 1 是函数y=ax在R上为减函数的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知向量 =（2，3）， =（﹣1，2），若﹣2 与非零向量m +n 共线，则等于（）A.﹣2B.2C.﹣D.4.如图是一个几何体的三视图，则这个几何体的表面积是（）A.84B.C.D.5.已知平面与平面交于直线l，且直线a ，直线b ，则下列命题错误的是（）A.若，a b，且b与l不垂直，则a lB.若，b l，则a bC.若a b，b l，且a与l不平行，则D.若a l，b l，则6.已知函数f（x）=sin（2x+ ），其中为实数，若f（x） |f（）|对x R 恒成立，且f（） f（），则f（x）的单调递增区间是（）A.[k ﹣，k + ]（k Z）B.[k ，k + ]（k Z）C.[k + ，k + ]（k Z）D.[k ﹣，k ]（k Z）7.已知实数列{an}是等比数列，若a2a5a8=﹣8，则 + + （）A.有值B.有最小值C.有值D.有最小值8.已知F1，F2分别是双曲线C：﹣ =1（a 0，b 0）的左、右焦点，其离心率为e，点B的坐标为（0，b），直线F1B与双曲线C的两条渐近线分别交于P、Q两点，线段PQ的垂直平分线与x轴，直线F1B的交点分别为M，R，若△RMF1与△PQF2的面积之比为e，则双曲线C的离心率为（）A. B. C.2 D.二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.9.已知loga2=m，loga3=n，则a2m+n= ，用m，n表示log46为 .10.已知抛物线x2=4y的焦点F的坐标为，若M是抛物线上一点，|MF|=4，O为坐标原点，则 MFO= .11.若函数f（x）= 为奇函数，则a= ，f（g（﹣2））= .12.对于定义在R上的函数f（x），如果存在实数a，使得f（a+x） f（a﹣x）=1对任意实数x R恒成立，则称f（x）为关于a的倒函数 .已知定义在R 上的函数f（x）是关于0和1的倒函数，且当x [0，1]时，f（x）的取值范围为[1，2]，则当x [1，2]时，f（x）的取值范围为，当x [﹣2022，2022]时，f（x）的取值范围为 .13.已知关于x的方程x2+ax+2b﹣2=0（a，b R）有两个相异实根，若其中一根在区间（0，1）内，另一根在区间（1，2）内，则的取值范围是 .14.若正数x，y满足x2+4y2+x+2y=1，则xy的值为 .15.在△ABC中， BAC=10 ， ACB=30 ，将直线BC绕AC旋转得到B1C，直线AC绕AB旋转得到AC1，则在所有旋转过程中，直线B1C与直线AC1所成角的取值范围为 .三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.16.在△ABC中，角A，B，C所对的边分别是a，b，c，且a=2，2cos2+sinA= .（Ⅰ）若满足条件的△ABC有且只有一个，求b的取值范围；（Ⅱ）当△ABC的周长取值时，求b的值.17.如图，在多面体EF﹣ABCD中，ABCD，ABEF均为直角梯形，，DCEF为平行四边形，平面DCEF 平面ABCD.（Ⅰ）求证：DF 平面ABCD；（Ⅱ）若△ABD是等边三角形，且BF与平面DCEF所成角的正切值为，求二面角A﹣BF﹣C的平面角的余弦值.18.已知函数f（x）=x2﹣1.（1）对于任意的1 x 2，不等式4m2|f（x）|+4f（m） |f（x﹣1）|恒成立，求实数m的取值范围；（2）若对任意实数x1 [1，2].存在实数x2 [1，2]，使得f（x1）=|2f（x2）﹣ax2|成立，求实数a的取值范围.19.已知F1，F2为椭圆的左、右焦点，F2在以为圆心，1为半径的圆C2上，且|QF1|+|QF2|=2a.（Ⅰ）求椭圆C1的方程；（Ⅱ）过点P（0，1）的直线l1交椭圆C1于A，B两点，过P与l1垂直的直线l2交圆C2于C，D两点，M为线段CD中点，求△MAB面积的取值范围.20.对任意正整数n，设an是方程x2+ =1的正根.求证：（1）an+1 an；（2） + + + 1+ + + + .2022-2022学年浙江省宁波市高三（上）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合M={0，1，2，3，4}，N={x|1A.{1}B.{2，3}C.{0，1}D.{2，3，4}【考点】交集及其运算.【分析】求出N中不等式的解集确定出N，找出M与N的交集即可.【解答】解：由N中不等式变形得：log22=1解得：0∵M={0，1，2，3，4}，M N={1}，故选：A.2.已知a R，则 |a﹣1|+|a| 1 是函数y=ax在R上为减函数的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】先求出不等式|a﹣1|+|a| 1的解集，结合指数函数的性质判断充分必要性即可.【解答】解：a 0时：|a﹣1|+|a|=1﹣a﹣a 1，解得：a 0，无解，0 a 1时：|a﹣1|+|a|=1﹣a+1=1 ，成立，a 1时：|a﹣1|+|a|=2a﹣1 1，解得：a 1，无解，故不等式的解集是a [0，1]，若函数y=ax在R上为减函数，则a （0，1），故 |a﹣1|+|a| 1 是函数y=ax在R上为减函数的必要不充分条件.3.已知向量 =（2，3）， =（﹣1，2），若﹣2 与非零向量m +n 共线，则等于（）A.﹣2B.2C.﹣D.【考点】平面向量共线（平行）的坐标表示.【分析】先求出﹣2 和m +n ，再由向量共线的性质求解.【解答】解：∵向量 =（2，3）， =（﹣1，2），﹣2 =（2，3）﹣（﹣2，4）=（4，﹣1），m +n =（2m﹣n，3m+2n），∵ ﹣2 与非零向量m +n 共线，，解得14m=﹣7n， =﹣ .故选：C.4.如图是一个几何体的三视图，则这个几何体的表面积是（）A.84B.C.D.【考点】由三视图求面积、体积.【分析】几何体为侧放的五棱柱，底面为正视图中的五边形，棱柱的高为4.【解答】由三视图可知几何体为五棱柱，底面为正视图中的五边形，高为4.所以五棱柱的表面积为（4 4﹣） 2+（4+4+2+2+2 ） 4=76+48 .故选B.5.已知平面与平面交于直线l，且直线a ，直线b ，则下列命题错误的是（）A.若，a b，且b与l不垂直，则a lB.若，b l，则a bC.若a b，b l，且a与l不平行，则D.若a l，b l，则【考点】空间中直线与平面之间的位置关系.【分析】根据空间直线和平面平行或垂直以及平面和平面平行或者垂直的性质和判定定理进行判断即可.【解答】解：A.若，a b，且b与l不垂直，则a l，正确B.若，b l，则b ，∵a ， a b，正确C.∵a与l不平行， a与l相交，∵a b，b l， b ，则正确.D.若a l，b l，不能得出，因为不满足面面垂直的条件，故D错误，故选：D6.已知函数f（x）=sin（2x+ ），其中为实数，若f（x） |f（）|对x R 恒成立，且f（） f（），则f（x）的单调递增区间是（）A.[k ﹣，k + ]（k Z）B.[k ，k + ]（k Z）C.[k + ，k + ]（k Z）D.[k ﹣，k ]（k Z）【考点】函数y=Asin（ x+ ）的图象变换.【分析】由若对x R恒成立，结合函数最值的定义，我们易得f（）等于函数的值或最小值，由此可以确定满足条件的初相角的值，结合，易求出满足条件的具体的值，然后根据正弦型函数单调区间的求法，即可得到答案.【解答】解：若对x R恒成立，则f（）等于函数的值或最小值即2 + =k + ，k Z则 =k + ，k Z又即sin 0令k=﹣1，此时 = ，满足条件令2x [2k ﹣，2k + ]，k Z解得x故选C7.已知实数列{an}是等比数列，若a2a5a8=﹣8，则 + + （）A.有值B.有最小值C.有值D.有最小值【考点】等比数列的通项公式.【分析】先求出a5=﹣2，再由 + + =1+ + ，利用均值定理能求出 + + 有最小值 .【解答】解：∵数列{an}是等比数列，a2a5a8=﹣8，，解得a5=﹣2，+ + = + + =1+ + 1+2 =1+2 =1+2 = ，+ + 有最小值 .故选：D.8.已知F1，F2分别是双曲线C：﹣ =1（a 0，b 0）的左、右焦点，其离心率为e，点B的坐标为（0，b），直线F1B与双曲线C的两条渐近线分别交于P、Q两点，线段PQ的垂直平分线与x轴，直线F1B的交点分别为M，R，若△RMF1与△PQF2的面积之比为e，则双曲线C的离心率为（）A. B. C.2 D.【考点】双曲线的简单性质.【分析】分别求出P，Q，M的坐标，利用△RMF1与△PQF2的面积之比为e，|MF2|=|F1F2|=2c，可得3c=xM= ，即可得出结论.【解答】解：由题意，|OB|=b，|O F1|=c. kPQ= ，kMR=﹣ .直线PQ为：y= （x+c），与y= x.联立得：Q（，）；与y=﹣ x.联立得：P（，）.PQ的中点为（，），直线MR为：y﹣ =﹣（x﹣），令y=0得：xM= ，又△RMF1与△PQF2的面积之比为e， |MF2|=|F1F2|=2c， 3c=xM= ，解之得：e2= ，e=故选：A.二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.9.已知loga2=m，loga3=n，则a2m+n= 12 ，用m，n表示log46为 .【考点】对数的运算性质.【分析】利用指数、对数的性质、运算法则和换底公式求解.【解答】解：∵loga2=m，loga3=n， am=2，an=3，a2m+n=（am）2 an=22 3=12，log46= = = .故答案为：12， .10.已知抛物线x2=4y的焦点F的坐标为（0，1），若M是抛物线上一点，|MF|=4，O为坐标原点，则 MFO= 或 .【考点】抛物线的简单性质.【分析】利用抛物线的方程与定义，即可得出结论.【解答】解：抛物线x2=4y的焦点在y轴上，且p=1，焦点坐标为（0，1）；∵M是抛物线上一点，|MF|=4，M（ 2 ，3），M（2 ，3），kMF= = ， MFO=M（﹣2 ，3），kMF=﹣ =﹣， MFO=故答案为：（0，1），或 .11.若函数f（x）= 为奇函数，则a= 0 ，f（g（﹣2））= ﹣25 .【考点】函数奇偶性的性质；函数的值.【分析】利用分段函数，结合函数的奇偶性，即可得出结论.【解答】解：由题意，a=f（0）=0.设x 0，则﹣x 0，f（﹣x）=x2﹣2x+1=﹣f（x），g（2x）=﹣x2+2x﹣1，g（﹣2）=﹣4，f（g（﹣2））=f（﹣4）=﹣16﹣8﹣1=﹣25.故答案为：0，﹣25.12.对于定义在R上的函数f（x），如果存在实数a，使得f（a+x） f（a﹣x）=1对任意实数x R恒成立，则称f（x）为关于a的倒函数 .已知定义在R 上的函数f（x）是关于0和1的倒函数，且当x [0，1]时，f（x）的取值范围为[1，2]，则当x [1，2]时，f（x）的取值范围为 [ ，1] ，当x [﹣2022，2022]时，f（x）的取值范围为 [ ，2] .【考点】抽象函数及其应用.【分析】根据倒函数的定义，建立两个方程关系，根据方程关系判断函数的周期性，利用函数的周期性和函数的关系进行求解即可得到结论.【解答】解：若函数f（x）是关于0和1的倒函数，则f（x） f（﹣x）=1，则f（x） 0，且f（1+x） f（1﹣x）=1，即f（2+x） f（﹣x）=1，即f（2+x） f（﹣x）=1=f（x） f（﹣x），则f（2+x）=f（x），即函数f（x）是周期为2的周期函数，若x [0，1]，则﹣x [﹣1，0]，2﹣x [1，2]，此时1 f（x） 2∵f（x） f（﹣x）=1，f（﹣x）= [ ，1]，∵f（﹣x）=f（2﹣x） [ ，1]，当x [1，2]时，f（x） [ ，1].即一个周期内当x [0，2]时，f（x） [ ，2].当x [﹣2022，2022]时，f（x） [ ，2].故答案为：[ ，1]，[ ，2].13.已知关于x的方程x2+ax+2b﹣2=0（a，b R）有两个相异实根，若其中一根在区间（0，1）内，另一根在区间（1，2）内，则的取值范围是 .【考点】一元二次方程的根的分布与系数的关系.【分析】由题意知，从而转化为线性规划问题求解即可.【解答】解：令f（x）=x2+ax+2b﹣2，由题意知，，作其表示的平面区域如下，，的几何意义是点A（1，4）与阴影内的点的连线的斜率，直线m过点B（﹣3，2），故km= = ；直线l过点C（﹣1，1），故kl= = ；结合图象可知，的取值范围是；故答案为： .14.若正数x，y满足x2+4y2+x+2y=1，则xy的值为 .【考点】基本不等式.【分析】由题意和基本不等式可得1=x2+（2y）2+x+2y 2 x 2y+2 ，解关于的一元二次不等式可得.【解答】解：∵正数x，y满足x2+4y2+x+2y=1，1=x2+4y2+x+2y=x2+（2y）2+x+2y 2 x 2y+2 ，当且仅当x=2y时取等号.变形可得2（）2+2 ﹣1 0，解得，结合 0可得0 ，平方可得2xy （）2= ，xy ，即xy的值为，故答案为：15.在△ABC中， BAC=10 ， ACB=30 ，将直线BC绕AC旋转得到B1C，直线AC绕AB旋转得到AC1，则在所有旋转过程中，直线B1C与直线AC1所成角的取值范围为 [10 ，50 ] .【考点】异面直线及其所成的角.【分析】平移CB1到A处，由已知得 B1CA=30 ， B1AC=150 ，0 C1AC20 ，由此能求出直线B1C与直线AC1所成角的取值范围.【解答】解：∵在△ABC中， BAC=10 ， ACB=30 ，将直线BC绕AC旋转得到B1C，直线AC绕AB旋转得到AC1，如图，平移CB1到A处，B1C绕AC旋转，B1CA=30 ， B1AC=150 ，AC1绕AB旋转， 0 C1AC 2 CAB，0 C1AC 20 ，设直线B1C与直线AC1所成角为，则 B1AC﹣ C1AC B1AC+ C1AC，∵130 B1AC﹣ C1AC 150 ，150 B1AC+ C1AC 170 ，10 50 或130 170 （舍）.故答案为：[10 ，50 ].三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.16.在△ABC中，角A，B，C所对的边分别是a，b，c，且a=2，2cos2+sinA= .（Ⅰ）若满足条件的△ABC有且只有一个，求b的取值范围；（Ⅱ）当△ABC的周长取值时，求b的值.【考点】正弦定理；余弦定理.【分析】（Ⅰ）由条件利用三角恒等变换求得cosA 和sinA 的值，结合满足条件的△ABC有且只有一个可得a=bsinA 或 a b，由此求得b的范围.（Ⅱ）△ABC的周长为a+b+c，利用余弦定理、基本不等式求得周长2+b+c 值为2+2 ，此时，b= =c.【解答】解：（Ⅰ）△ABC中，角A，B，C所对的边分别是a，b，c，且a=2，2cos2 +sinA= ，2 +sinA= ，即 2 +sinA= ， cosA﹣sinA= ，平方可得sin2A= ， cosA+sinA= = ，求得cosA= ，sinA= （，），结合满足条件的△ABC有且只有一个， A （，）.且a=bsinA，即2= b，即 b= ；或 a b，即0（Ⅱ）由于△ABC的周长为a+b+c，由余弦定理可得22=b2+c2﹣2bc =（b+c）2﹣ bc （b+c）2﹣ = （b+c）2，b+c =2 ，当且仅当b=c时，取等号，此时，三角形的周长为 2+b+c为2+2 ，故此时b= .17.如图，在多面体EF﹣ABCD中，ABCD，ABEF均为直角梯形，，DCEF为平行四边形，平面DCEF 平面ABCD.（Ⅰ）求证：DF 平面ABCD；（Ⅱ）若△ABD是等边三角形，且BF与平面DCEF所成角的正切值为，求二面角A﹣BF﹣C的平面角的余弦值.【考点】二面角的平面角及求法；直线与平面垂直的判定.【分析】（Ⅰ）推导出AB 平面BCE，AB∥CD∥EF，从而CD 平面BCE，进而CD CE，由CE∥DF，得CD DF，由此能证明DF 平面ABCD.（Ⅱ）法1：过C作CH BE交BE于H，HK BF交BF于K，推导出 HKC为C﹣BF﹣E的平面角，由此能求出二面角A﹣BF﹣C的平面角的余弦值.（Ⅱ）法2：以C为原点，CD，CB，CE所在直线为x，y，z轴，建立空间直角坐标系.不妨设CD=1，利用向量法能求出二面角A﹣BF﹣C的平面角的余弦值.【解答】证明：（Ⅰ）因为，所以AB 平面BCE，又EF∥CD，所以EF∥平面ABCD，从而有AB∥CD∥EF，所以CD 平面BCE，从而CD CE，又CE∥DF，所以CD DF，又平面DCEF 平面ABCD，所以DF 平面ABCD.解：（Ⅱ）解法1：过C作CH BE交BE于H，HK BF交BF于K，因为AB 平面BCE，所以CH AB，从而CH 平面ABEF，所以CH BF，从而BF 平面CHK，所以BF KH即 HKC为C﹣BF﹣E的平面角，与 A﹣BF﹣C的平面角互补. 因为BC DCEF，所以BF与平面DCEF所成角为 BFC.由，所以2CB2=CD2+CE2，由△ABD是等边三角形，知 CBD=30 ，所以令CD=a，所以， .所以， .所以二面角A﹣BF﹣C的平面角的余弦值为 .（Ⅱ）解法2：因为CB，CD，CE两两垂直，以C为原点，CD，CB，CE所在直线为x，y，z轴，如图建立空间直角坐标系.不妨设CD=1.因为BC DCEF，所以BF与平面DCEF所成角为 BFC.由，所以2CB2=CD2+CE2，由△ABD是等边三角形，知 CBD=30 ，所以，，平面ABF的一个法向量，平面CBF的一个法向量则，且取则 .二面角A﹣BF﹣C的平面角与的夹角互补.所以二面角A﹣BF﹣C的平面角的余弦值为 .18.已知函数f（x）=x2﹣1.（1）对于任意的1 x 2，不等式4m2|f（x）|+4f（m） |f（x﹣1）|恒成立，求实数m的取值范围；（2）若对任意实数x1 [1，2].存在实数x2 [1，2]，使得f（x1）=|2f（x2）﹣ax2|成立，求实数a的取值范围.【考点】函数恒成立问题；二次函数的性质.【分析】（1）由题意可得4m2（|x2﹣1|+1| 4+|x2﹣2x|，由1 x 2，可得4m2 ，运用二次函数的最值的求法，可得右边函数的最小值，解不等式可得m 的范围；（2）f（x）在[1，2]的值域为A，h（x）=|2f（x）﹣ax|的值域为B，由题意可得A B.分别求得函数f（x）和h（x）的值域，注意讨论对称轴和零点，与区间的关系，结合单调性即可得到值域B，解不等式可得a的范围.【解答】解：（1）对于任意的1 x 2，不等式4m2|f（x）|+4f（m） |f（x ﹣1）|恒成立，即为4m2（|x2﹣1|+1| 4+|x2﹣2x|，由1 x 2，可得4m2 ，由g（x）= =4（ + ）2﹣，当x=2，即 = 时，g（x）取得最小值，且为1，即有4m2 1，解得﹣ m ；（2）对任意实数x1 [1，2].存在实数x2 [1，2]，使得f（x1）=|2f（x2）﹣ax2|成立，可设f（x）在[1，2]的值域为A，h（x）=|2f（x）﹣ax|的值域为B，可得A B.由f（x）在[1，2]递增，可得A=[0，3]；当a 0时，h（x）=|2x2﹣ax﹣2|=2x2﹣ax﹣2，（1 x 2），在[1，2]递增，可得B=[﹣a，6﹣2a]，可得﹣a 0 3 6﹣2a，不成立；当a=0时，h（x）=2x2﹣2，（1 x 2），在[1，2]递增，可得B=[0，6]，可得0 0 3 6，成立；当01（负的舍去），h（x）在[1， ]递减，[ ，2]递增，即有h（x）的值域为[0，h（2）]，即为[0，6﹣2a]，由0 0 3 6﹣2a，解得0当2即有h（x）的值域为[0，h（2）]，即为[0，a]，由0 0 3 a，解得a=3；当3由2a﹣6 0 3 a，无解，不成立；当4由2a﹣6 0 3 2a，不成立；当6由a 0 3 2a，不成立；当a 8时，h（x）在[1，2]递增，可得B=[a，2a﹣6]， A B不成立.综上可得，a的范围是0 a 或a=3.19.已知F1，F2为椭圆的左、右焦点，F2在以为圆心，1为半径的圆C2上，且|QF1|+|QF2|=2a.（Ⅰ）求椭圆C1的方程；（Ⅱ）过点P（0，1）的直线l1交椭圆C1于A，B两点，过P与l1垂直的直线l2交圆C2于C，D两点，M为线段CD中点，求△MAB面积的取值范围.【考点】椭圆的简单性质.【分析】（Ⅰ）圆C2的方程为，由此圆与x轴相切，求出a，b的值，由此能求出椭圆C1的方程.（Ⅱ）设l1：x=t（y﹣1），则l2：tx+y﹣1=0，与椭圆联立，得（t2+2）y2﹣2t2y+t2﹣4=0，由此利用弦长公式、点到直线距离公式，结合已知条件能求出△MAB面积的取值范围.【解答】（本题满分15分）解：（Ⅰ）圆C2的方程为，此圆与x轴相切，切点为，即a2﹣b2=2，且，又|QF1|+|QF2|=3+1=2a.a=2，b2=a2﹣c2=2椭圆C1的方程为 .（Ⅱ）当l1平行x轴的时候，l2与圆C2无公共点，从而△MAB不存在；设l1：x=t（y﹣1），则l2：tx+y﹣1=0.由，消去x得（t2+2）y2﹣2t2y+t2﹣4=0，则 .又圆心到l2的距离，得t2 1.又MP AB，QM CDM到AB的距离即Q到AB的距离，设为d2，即 .△MAB面积令则 .△MAB面积的取值范围为 .20.对任意正整数n，设an是方程x2+ =1的正根.求证：（1）an+1 an；（2） + + + 1+ + + + .【考点】数列的应用.【分析】（1）解方程可得an= ，再由分子有理化，结合，在n N*上递减，即可得证；（2）求出 = ，分析法可得，累加并运用不等式的性质即可得证.【解答】解：（1）an是方程x2+ =1的正根，解得an= ，由分子有理化，可得an== ，由，在n N*上递减，可得an为递增数列，即为an+1 an；（2）证明：由an= ，可得= ，由 2n﹣11+4n2﹣4n 1+4n2 ﹣4n 0，显然成立，即有 + + + 1+ + + +1+ + + + .。

大一上学期高数期末考试一、单项选择题 (本大题有4小题， 每小题4分， 共16分） 1. )(0),sin (cos )(　处有则在设=+=x x x x x f 。

(A ）(0)2f '= （B)(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.(A)()()x x αβ与是同阶无穷小，但不是等价无穷小; (B ）()()x x αβ与是等价无穷小；(C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则( ）.(A ）函数()F x 必在0x =处取得极大值； （B ）函数()F x 必在0x =处取得极小值；(C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点； （D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点.4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x (B ）222x+（C ）1x - （D ）2x +。

二、填空题(本大题有4小题,每小题4分,共16分） 5. =+→xx x sin 2)31(l i m .6. ,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则。

7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ 。

8. =-+⎰21212211arcsin －dx xx x 。

三、解答题(本大题有5小题，每小题8分,共40分）9. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y 。