第三章 正交试验设计(1)-正交试验及直观分析
- 格式:ppt
- 大小:466.50 KB
- 文档页数:29


正交试验设计和分析方法研究一、本文概述正交试验设计是一种高效、系统的试验设计方法,广泛应用于科学研究、工程实践以及社会调查等领域。
通过正交表的正交性、均匀分散性和整齐可比性,正交试验设计能够在众多试验因素中快速找出关键因素,优化试验方案,提高试验效率。
本文旨在深入研究正交试验设计的理论基础,探讨其在实际应用中的优化策略,分析正交试验设计的优缺点,并展望其未来发展趋势。
本文首先介绍正交试验设计的基本原理和常用正交表,然后详细阐述正交试验设计的步骤和方法,接着通过案例分析展示正交试验设计在不同领域的应用实践,最后对正交试验设计的未来发展进行展望,以期为相关领域的研究和实践提供有益的参考和借鉴。
二、正交试验设计基本原理正交试验设计是一种高效、系统的试验设计方法,其核心在于利用正交表来安排试验,通过对试验因素与水平进行全面、均匀的搭配,从而找出最佳的试验方案。
正交试验设计的基本原理主要包括以下几点:正交性原理:正交表具有正交性,即表中的每一行(或列)所代表的因素水平组合都是唯一的,且在整个表中均匀分布。
这种正交性保证了试验点在试验范围内均匀分布,从而能够全面反映试验因素与水平的变化情况。
代表性原理:正交表中的每一行都代表一组试验因素与水平的组合,这些组合在试验范围内具有代表性。
通过选择适当的正交表,可以在较少的试验次数下获得较为全面的试验结果。
综合可比性原理:正交表中的每一列都对应一个试验因素,不同列之间的因素是相互独立的。
这意味着每个因素在不同水平下的效果可以单独进行分析和比较,从而便于找出影响试验结果的主要因素及其最佳水平。
分析简便性原理:正交试验设计的结果分析简便易行,可以通过直观分析或方差分析等方法快速得出结论。
直观分析法可以直接从正交表中观察出各因素在不同水平下的效果,而方差分析法则可以进一步检验各因素对试验结果的影响程度。
正交试验设计通过合理利用正交表的性质,实现了试验的高效、系统和全面。
在实际应用中,只需根据试验需求选择合适的正交表,按照表中的安排进行试验,并对试验结果进行简便的分析,即可得出较为准确的结论。





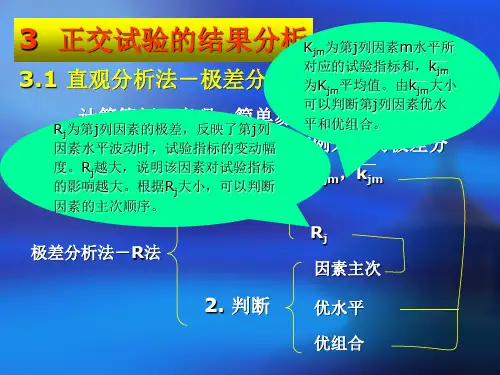
正交试验一.无交互作用的正交试验:1.(1)直观分析表1直观分析计算表A B C D 时间1 1 1 1 1 1852 1 2 2 2 1803 1 3 3 3 1794 2 1 2 3 1835 2 2 3 1 1796 2 3 1 2 1827 3 1 3 2 1608 3 2 1 3 1659 3 3 2 1 150T1 544 528 532 514T2 544 524 513 5221563T475 511 518 5271T181.33 174.67 171 174173.672T158.3 170.33 172.67 175.673R 23 5.67 6.33 4.33从四个因子的极差可知A的影响最大,之后依次是因子C,B,D。
则为提高树脂的使用时间,比较各个因子在各水平下的均值,认为最佳组合为A1B1C1D3或A2B1C1D3。
(2)水平均值图图1水平均值图从水平均值图知,因子A的水平1,2相等,且与水平3差异较大,因子B,C,D中最高的水平分别为1,1,3,则认为最佳组合为A1B1C1D3或A2B1C1D32.(1)表 2直观分析计算表一水平 二水平 三水平 1 1 1 1 1 2 1 2 2 2 3 1 3 3 3 4 2 1 2 3 5 2 2 3 1 6 2 3 1 2 7 3 1 3 2 8 3 2 1 3 9 3 3 2 1 T 1 56.66667 70 65 68 T 2 66.66667 71.66667 72.33333 69 T 3 85.33333 67 71.33333 71.66667R28.666674.6666677.33333332248公斤,催化剂取已,可使试验提高效率。
图 2水平均值图(2)表 3方差分析表来源 平方和S 自由度f均方和MS F 比 因子A 1270.22 2 635.11 58.93 因子B 33.55 2 16.78 1.557 因子C 94.89 2 47.44 4.402 误差e 21.55 2 10.78 T1420.228F 0.95(2,2)=19.0由上表可知,因子A 在显著性水平0.05上是显著的,因子B 和因子C 是不显著的。
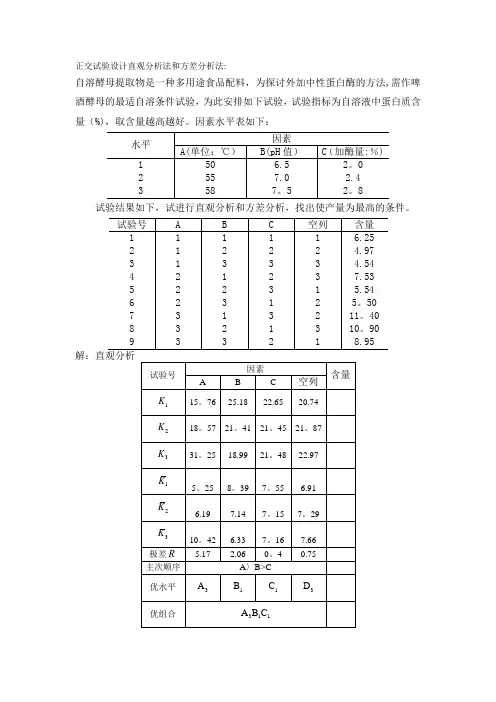
正交试验设计直观分析法和方差分析法:
自溶酵母提取物是一种多用途食品配料,为探讨外加中性蛋白酶的方法,需作啤酒酵母的最适自溶条件试验,为此安排如下试验,试验指标为自溶液中蛋白质含量(%),取含量越高越好。
因素水平表如下:
试验结果如下,试进行直观分析和方差分析,找出使产量为最高的条件。
A B C e df df df df ====3-1=2
2A A A SS MS df =
=45.422.72=,2B B B SS MS df ==6.49
3.232=, 2C C C SS MS df =
=0.310.1552=,2e e e
SS MS df ==0.83
0.4152= 因为22
2C e MS MS <,所以因素C 的偏差平方和、自由度并入误差的偏差平方和、自由度
因素A 高度显著,因素B 显著,因素C 不显著.本试验指标越大越好.对因素A 、B 分析,确定优水平为3A 、1B ;因素C 的水平改变对试验结果几乎无影响,从经济角度考虑,选1C 。
优水平组合为311A B C 。
即温度为58℃,pH 值为6。
5,加酶量为2。
0%.。

正交试验设计及结果分析正交试验设计(Orthogonal design)是一种组织实验研究的方法,通过在有限的试验条件下,系统地研究多个影响因素及其之间的相互作用,以得出客观科学的结论。
本文将介绍正交试验设计的基本原理、优势以及结果分析的方法。
正交试验设计的基本原理是通过对因素和水平的选择进行系统设计,使实验的观测结果具有统计意义,并能准确地区分不同因素对结果的影响。
正交试验设计的特点是因素之间相互独立,通过合理的分配和排列,能够明确地检验各个因素的主效应、交互效应以及误差效应。
正交试验设计的主要目的是全面、有效地获取实验结果,以便进行相应的数据分析和参数估计。
正交试验设计的优势在于可以在较小的试验规模和资源成本的情况下,获得较精确的试验结果。
由于因素之间相互独立,可以通过较少的试验次数得到充分的信息,从而快速筛选出有意义和重要的因素及其相应的水平。
同时,正交试验设计还能在实验中考虑因素之间的交互作用,从而更准确地预测实际情况下的因素效应。
进行正交试验设计时,首先需要确定所研究问题的因素和水平。
然后,根据所选因素和水平的数量确定试验矩阵的大小和形状。
通常采用正交设计表的方法对试验矩阵进行构造,以保证各个因素和水平的均衡和合理分布。
在实验过程中,根据设计要求,进行不同因素和水平的试验组合,记录并整理实验数据。
对正交试验设计的结果进行分析时,需要根据研究目的选择适当的统计方法。
主要包括方差分析、回归分析、均方差分解等方法。
通常可以采用多因素方差分析(ANOVA)方法,评估各个因素和水平对结果的影响程度,并检验各个因素的显著性。
此外,还可以进行主效应和交互效应的分析,了解各个因素之间的相互作用情况。
通过分析结果,可以确定主要因素和水平,为后续实验和优化提供参考。
总之,正交试验设计是一种有效的设计和分析方法,能够在较小的试验规模和资源成本下,获取较精确的实验结果。
通过合理选择因素和水平,并进行系统的设计和分析,能够全面地了解各个因素对结果的影响,为实际问题的解决提供科学依据。
正交试验设计及分析(多实现途径)引言概述:正交试验设计是一种重要的统计方法,用于确定实验中不同因素对结果的影响。
它可以帮助研究者系统地设计实验,降低实验数量和成本,并提供可靠的分析结果。
本文将介绍正交试验设计的概念、原理,以及多种实现途径,以便读者根据自身需求选择合适的方法进行实验。
正文内容:1.正交试验设计的概念和原理:1.1定义:正交试验设计是一种通过系统地变动因素水平来确定因素对结果的影响的方法。
它将多个因素分解为一些离散的水平,以便在有限实验中进行测试。
1.2原理:正交试验设计基于正交矩阵的原理,该矩阵具有特定的数学性质,可以保证不同因素之间的相互独立性,从而减少实验数量。
2.正交试验设计的多实现途径:2.1Taguchi方法:Taguchi方法是一种常用的正交试验设计方法,它通过选择最优的因素水平组合来优化结果的表现。
它能够在较少的实验次数下找到最佳的因素配置。
2.2BoxBehnken设计:BoxBehnken设计是一种常用的三水平正交试验设计方法,适用于3个或更多个因素的试验。
它通过正交矩阵将因素水平组合成三水平,并通过优化方法确定最佳结果。
2.3中心组合设计:中心组合设计是一种将中心点设置为固定因素水平的正交试验设计方法。
该设计方法可以估计因素对结果的线性和二次的影响,适用于连续和离散因素。
2.4贝叶斯优化设计:贝叶斯优化设计是一种基于贝叶斯统计模型的正交试验设计方法。
它能够在先验知识不完全或验证数据有限的情况下,利用概率推论来确定最佳因素配置。
3.正交试验设计的分析方法:3.1方差分析:方差分析是一种常用的正交试验设计分析方法,用于确定各个因素之间的显著性差异。
它通过计算方差的比值来判断因素对结果的影响程度。
3.2回归分析:回归分析是一种统计方法,用于描述和预测因变量与一个或多个自变量之间的关系。
在正交试验设计中,回归分析可以用来确定因素对结果的线性和非线性影响。
3.3主效应图:主效应图是一种简明直观的分析方法,通过图形展示各个因素对结果的平均水平差异。
正交试验设计与直观分析:正交试验直观分析6.正交实验设计与直观分析一、目的和结论目的:做这个实验是为了什么.结论:从实验分析后得出的结论,相当于总结性的话。
二、结果和指标结果:从实验中得出的数据或现象,记录下来。
指标:用来衡量试验效果的质量指标。
三、因素和水平因素:实验中不同考察条件,比如温度,PH,浓度等。
水平:实验中因素所取的考察点。
四、处理和单位处理:实验中所要操纵的自变量的变化。
五、重复和平行同时做的同一样品试验是平行试验,不同时做的不同样品试验是重复六、试验设计的原则 1、重复:同时做的同一样品试验是平行试验,不同时做的不同样品试验是重复 2、随机化:试验单元随机进入试验中,试验顺序等随机 3、区组化:使试验中对结果有影响但不是重点监测的因素保持一致(局部一致),使试验结果无显著影响。
4、对照:优化实验可以没有对照空白对照、条件对照、方法对照七、试验类型 1、单因素序贯试验设计 2、全面设计 3、正交试验设计正交实验设计:利用正交表科学地安排与分析多因素试验的方法 u 正交表:三种分析方法:直观分析、方差分析、回归分析 1) 等水平正交表:各因素的水平数是相等的。
特点:l 表中任一列,不同的数字出现的次数相同。
l 表中任意两列,各种同行数字对出现的次数相同 2) 混合水平正交表:重点考察的因素可多取一些水平,其他因素的水平数可适当减少。
重要性质:l 表中任一列,不同的数字出现的次数相同。
l 每两列,同行两个数字组成的各种不同的水平搭配出现的次数是相同的,但不同的两列间组成的水平搭配种类及出现次数是不完全相同的。
各因素的水平数不完全相同的正交表:正交表L8(41ⅹ24)实验号列号 1 2 3 4 5 11 1 1 1 12 1 2 2 2 23 2 1 1 2 24 22 2 1 1 53 1 2 1 2 6 3 2 1 2 1 74 1 2 2 1 8 4 2 1 1 2 u 正交实验设计的基本步骤: ²明确实验目的,确定评价指标²挑选因素,确定水平²选正交表,进行表头设计 n 选正交表: 水平数与正交表对应的水平数一致 l 因素数小于等于正交表列数 l 选较小的表 n表头设计:一个因素占有一列;不同因素占不同列(随机排列)²明确设计方案,进行实验,得到结果²对试验结果进行统计分析²进行验证试验,作进一步分析 4、正交试验设计的优点 1) 能均匀地挑选出代表性强的少数试验方案 2) 由少数试验结果,可以退出较优的方案 3) 可以得到试验结果之外的更多信息正交实验设计结果的直观分析法 1)、单指标正交试验设计及结果的直观分析选正交表表头设计明确实验方案按规定的方案做实验,得出试验结果计算极差,确定因素的主次顺序优方案的确定进行验证试验,作进一步的分析 2)、多指标正交试验设计及结果的直观分析 3)、交互作用 4)、混合水平单指标正交试验设计及其结果的直观分析根据试验指标的个数,可把正交试验设计分为单指标试验设计与多指标试验设计。