第3章指数函数与对数函数复习一(教案)

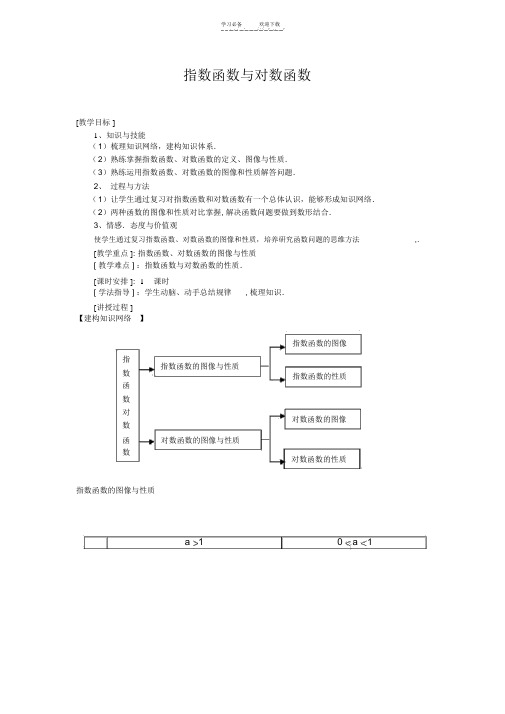
学习必备欢迎下载指数函数与对数函数[教学目标 ]1、知识与技能（1）梳理知识网络，建构知识体系．（2）熟练掌握指数函数、对数函数的定义、图像与性质．（3）熟练运用指数函数、对数函数的图像和性质解答问题．2、过程与方法（1）让学生通过复习对指数函数和对数函数有一个总体认识，能够形成知识网络．（2）两种函数的图像和性质对比掌握, 解决函数问题要做到数形结合．3、情感．态度与价值观使学生通过复习指数函数、对数函数的图像和性质，培养研究函数问题的思维方法,．[教学重点 ]: 指数函数、对数函数的图像与性质[ 教学难点 ] ：指数函数与对数函数的性质．[课时安排 ]: 1课时[ 学法指导 ] ：学生动脑、动手总结规律, 梳理知识．[讲授过程 ]【建构知识网络】指数函数的图像指指数函数的图像与性质数指数函数的性质函数对对数函数的图像数函对数函数的图像与性质数对数函数的性质指数函数的图像与性质a 10 a1图象（1）定义域：R（2）值域：(0,)性，即 x0 时y1（3）过点(0,1)质当 x>0 时 ,y>1；当 x<0 时 ,0<y<1当 x>0 时, 0<y<1 ；当 x<0 时, y>1（4）在R上是增函数（ 4）在R上是减函数对数函数的图像与性质函（ a>1）y log a x （0<a<1）y log a x数图像定义域（0， +∞）（ 0， +∞）值域R R单调性增函数减函数过定点（1， 0）（1，0）0<x<1 时， y<00<x<1 时， y>0取值范围x>1 时， y>0x>1 时， y<0例题 :一、定义域1例 1．求下列函数的定义域（ 1 ）y log 2(x 2) ;（2）y2 x214解 : （ 1 ）要使函数有意义 , 须使log2( x2)0,即 log 2 (x2)log 2 1 ,因为函数y log 2 x 为增函数,所以 x 21,x 1 ,所以函数的定义域为{x| x1}（ 2）要使函数有意义,须使2x1102 x 1 2 2 ,x12,x 1 ,所以函数4的定义域为 {x| x1}12练习 1:求下列函数的定义域（1）y;（ 2）y32xlg(x3)二、值域例 2．求下列函数的值域1（ 1）y 5 2x（ 2）y1 2 x（ 3）y log 1 (4x5)3分析 :要求函数的值域 ,必须先求函数的定义域,要在函数的定义域范围内求出．11解 :（ 1）函数y52x的定义域为 {x | x2} ,指数0 ,所以 y1,函数的值域为x2{y | y0, y1} ;（ 2）函数y1 2 x有意义 ,必须12x02x1x0 ,函数的定义域为 (,0] ,因为 2x0,0 1 2x1,所以函数的值域为[0,1)．（ 3 ）y log1(4x5) 要有意义,须使 4 x50x 5,函数的定义域为43{x | x 5} ,此时真数 4x50 ,所以函数的值域为R41x1x1练习 2: 求下列函数的值域（1）y1（ 2）y 1 （3） y ln32x51解 :（ 1）函数y31 x的值域为0 ，;x x11 有意义,则1所以函数的定义域为（ 2 ）函数y 1 0, x 022{x | x 0} ,值域为 [0,) ．（ 3）函数 y ln1 要有意义 ,须使1 0 x5,函数的定义域为 {x | x5} ,函5 x 5 x数的值域为 R ．三、单调性例 3．已知 f (x)1 log x 3 ， g( x) 2log x2 ,试比较 f ( x)和g( x) 的大小。

必修一第三章指数函数与对数函数复习教案一、教学目标1.了解指数函数和对数函数的定义及性质；2.掌握指数函数和对数函数的图像和性质；3.熟练运用指数函数和对数函数解决实际问题。

二、教学重点1.指数函数的定义与性质；2.对数函数的定义与性质；3.指数函数和对数函数的图像和性质。

三、教学内容1.指数函数1.指数函数的定义：$y=a^x$，其中a>0且a≠1，x是任意实数。

2.指数函数图像：-当0<a<1时，函数图像呈递减趋势，经过点(0,1)；-当a>1时，函数图像呈递增趋势，经过点(0,1)；3.指数函数的性质：-函数图像经过点(0,1)；-当x=0时，y=1；-指数函数在0<a<1时，取值范围为(0,+∞)，在a>1时，取值范围为(0,+∞)；-函数图像在经过点(0,1)时，若a>1，则过(1，a)；若0<a<1，则过(a,1)；-当x→+∞时，y→+∞；当x→-∞时，y→0。

2.对数函数1. 对数函数的定义：$y=log_{a}{x}$，其中 a > 0 且a≠1，x > 0。

2.对数函数图像：-当0<a<1时，函数图像呈递减趋势，过点(1,0)；-当a>1时，函数图像呈递增趋势，过点(1,0)。

3.对数函数的性质：-函数图像过点(1,0)；-对数函数取值范围为(-∞,+∞)；-函数图像在过点(1,0)时，若a>1，则过点(a,1)；若0<a<1，则过点(1/a,1)；-当x→+∞时，y→+∞；当x→0+时，y→-∞。

四、教学方法1.教师讲解结合示例引入指数函数和对数函数的定义及性质；2.布置题目，让学生互相讨论，并与学生一起解答问题；3.利用电子白板展示指数函数和对数函数的图像，让学生观察特点。

五、教学过程1.引入指数函数和对数函数的定义及性质，与学生一起讨论和提问；2.利用示例分别介绍指数函数和对数函数的图像和性质，解释每个关键点的含义；3.设计问题让学生自主思考并与同学讨论解决；4.利用电子白板展示指数函数和对数函数的图像，与学生进行互动讨论。

指数函数与对数函数的复习教学设计番禺区石碁中学邓胜旺一、教学内容和内容解析函数是贯穿高中数学的一条主线,也是数学高考重点考察的内容之一。

指数函数与对数函数是中学数学中五类基本初等函数中非常重要的两种，也是进一步学习研究函数的基础，是高考必考内容。

高考中既考查双基, 又考查对蕴含其中的函数思想、等价转化、分类讨论、数形结合等思想方法的理解与运用。

主要考查定义域、值域、图像以及指数函数与对数函数的主要性质；应用性质比较两个数的大小，以及解指数不等式与对数不等式、建立相应的函数模型解决实际问题等。

本部分试题既可以出选择题、填空题，也可以出解答题，出解答题时综合能力要求较高。

因此应做到能熟练掌握它们的图象与性质并能进行一定的综合运用。

本节课是在学生学习了指数函数、对数函数的基础上进一步学习研究指数函数、对数函数的性质与应用。

本节课通过训练来复习指数函数、对数函数，让学生进一步理解函数的概念与性质，学习函数模型研究和解决一些实际问题的方法。

逐步掌握中学数学中的数形结合、分类讨论、类比、化归的数学思想，进一步理解函数的概念与性质。

二、教学设计思想坚持以学生是学习的主体和教师是学习的主导的原则，体现“练在讲之前，讲在关键处”的思想，以师生、生生互动参与课堂的形式组织有效复习。

三、学情分析本次授课对象是仲元中学高一学生，属于广州市一组生源。

学生数学基础比较扎实，接受能力较强，通过前一段时间学习，已经掌握了一些研究函数的方法和基本的数学思想。

四、教学目标知识与技能：1.理解掌握指数函数、对数函数的概念、性质、图象及运算性质。

2.能够用指数函数和对数函数的概念、性质、图象解决问题。

3.学习函数模型研究和解决一些实际问题的方法。

过程与方法：通过对指数函数、对数函数的研究，加深对函数概念的理解，培养学生分类与讨论、数与形结合、类比等重要的数学思想、能力，学习函数模型研究和解决一些实际问题的方法。

情感态度与价值观：1.提高学生的认知水平，为学生塑造良好的数学认识结构。

教案：幂函数、指数函数和对数函数·对数及其运算法则第一章：幂函数1.1 幂函数的定义与性质定义：幂函数是一种形式的函数，可以表示为f(x) = x^a，其中a 是实数。

性质：幂函数的图像是一条曲线，随着a 的不同取值，曲线的形状也会发生变化。

当a > 1 时，函数在x > 0 的区间上是增函数；当0 < a < 1 时，函数在x > 0 的区间上是减函数；当a = 0 时，函数是常数函数；当a < 0 时，函数在x >0 的区间上是增函数。

1.2 幂函数的图像与性质图像：通过绘制不同a 值的幂函数图像，观察曲线的形状和变化趋势。

性质：当a > 0 时，函数在x = 0 时无定义，但在x > 0 的区间上有定义；当a < 0 时，函数在x = 0 时无定义，但在x < 0 的区间上有定义；当a 为正整数时，函数在x > 0 的区间上是增函数；当a 为负整数时，函数在x < 0 的区间上是增函数。

第二章：指数函数2.1 指数函数的定义与性质定义：指数函数是一种形式的函数，可以表示为f(x) = a^x，其中a 是正实数。

性质：指数函数的图像是一条曲线，随着x 的增大，曲线的值也会增大。

指数函数的图像经过点(0, 1)，并且随着a 的增大，曲线的斜率也会增大。

2.2 指数函数的图像与性质图像：通过绘制不同a 值的指数函数图像，观察曲线的形状和变化趋势。

性质：当a > 1 时，函数在整个实数域上是增函数；当0 < a < 1 时，函数在整个实数域上是减函数；指数函数的图像具有反射性，即f(x) = a^x 和f(x) = a^(-x) 的图像关于y 轴对称。

第三章：对数函数3.1 对数函数的定义与性质定义：对数函数是一种形式的函数，可以表示为f(x) = log_a(x)，其中a 是正实数。

性质：对数函数的图像是一条曲线，随着x 的增大，曲线的值也会增大。

一、1、本节课的重点分析：指数函数与对数函数的图像与性质。

2、本节课的难点分析：指数函数与对数函数的运用。

二、授课内容：一、知识归纳：1、指数函数、对数函数的定义；2、指数函数与对数函数的图像和性质；3、指数函数与对数函数的联系。

指数函数重难点：对分数指数幂的含义的理解，学会根式与分数指数幂的互化并掌握有理指数幂的运算性质；指数函数的性质的理解与应用，能将讨论复杂函数的单调性、奇偶性问题转化为讨论比较简单的函数的有关问题．考纲要求：①了解指数函数模型的实际背景；②理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算；③理解指数函数的概念，并理解指数函数的单调性与函数图像通过的特殊点；④知道指数函数是一类重要的函数模型．经典例题：求函数y =3322++-x x 的单调区间和值域．对数函数重难点：理解并掌握对数的概念以及对数式和指数式的相互转化，能应用对数运算性质及换底公式灵活地求值、化简；理解对数函数的定义、图象和性质，能利用对数函数单调性比较同底对数大小，了解对数函数的特性以及函数的通性在解决有关问题中的灵活应用．考纲要求：①理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用；②理解对数函数的概念；理解对数函数的单调性，掌握函数图像通过的特殊点；③知道对数函数是一类重要的函数模型；④了解指数函数xy a =与对数函数log a y x =互为反函数(),1a o a ≠ ． 幂函数重难点：掌握常见幂函数的概念、图象和性质，能利用幂函数的单调性比较两幂值的大小． 考纲要求：①了解幂函数的概念；②结合函数12321,,,,y x y x y x y y x x =====的图像，了解他们的变化情况．二、题型归纳：◆比较大小及解不等式：1、用不等号“ > ”、“ < ”填空：(1)log 0.56 ___ log 0.54 ;(2) log 812 ___ log 1211 ;(3) 若log 1.5m < log 1.5n , 则m___n ;(4) 若log 0.125m < log 0.125n , 则m___n ;2、解下列关于x 的不等式:(3) log 0.5x > log 0.5(1-x) (4) log 2(x+3) < 0◆求定义域和值域：3、求函数91312-=-x y 的定义域4、求下列函数定义域（1）y=(1-x) (2) y= (3) y=(4）= （5）32log x y = （6）)34(log 5.0-=x y ）5、例 f(x)=3x +5，则f -1(x)的定义域是 。

学员姓名年级高一辅导科目数学课程类型1对1任课老师班组课题指数函数与对数函数课型□预习课□同步课□复习课□习题课课次11 授课日期及时段教学目标重难点重点：难点：教学及学习方法教学方法：学习方法：教学内容【基础知识网络总结与巩固】本节考点：考点回顾考点一考点二考点三【上节知识回顾】【本节知识要点】1. 指数函数的图象和性质函数y＝a x(a>0，且a≠1)图象0<a<1a>1图象特征在x轴上方，过定点(0,1)性质定义域值域单调性函数值变化规律R(0，＋∞)减函数增函数当x＝0时，y＝1当x<0时，y>1；当x>0时，0<y<1当x<0时，0<y<1；当x>0时，y>12．对数函数的图象和性质y ＝log a xa >10<a <1图象性质定义域：(0，＋∞)值域：R过点(1,0)，即x ＝1时，y ＝0当x >1时，y >0 当0<x <1时，y <0 当x >1时，y <0 当0<x <1时，y >0 在(0，＋∞)上是增函数在(0，＋∞)上是减函数3.求解与指数函数、对数有关的复合函数问题，首先要熟知指数函数、对数函数的定义域、值域、单调性等相关性质，其次要明确复合函数的构成，涉及值域、单调区间、最值等问题时，都要借助“同增异减”这一性质分析判断，最终将问题归纳为内层函数相关的问题加以解决．【重难点例题启发与方法总结】典型例题剖析例1 求下列函数的定义域 (1)f (x )＝1－2log 6x ； (2)y ＝32x －1－19.【解析】(1)由1－2log 6x ≥0，解得log 6x ≤12⇒0＜x ≤6，故所求定义域为(0， 6 ]．(2)由32x －1－19≥0，得32x －1≥19＝3－2，∵y ＝3x 为增函数，∴2x －1≥－2，即x ≥－12，此函数的定义域为⎣⎡⎭⎫－12，＋∞. 变式训练 函数f (x )＝4－x 2＋log 2(x －1)的定义域是( ) A ．(1,2] B ．[1,2] C ．(1，＋∞) D ．[2，＋∞)【答案】A【解析】要使函数有意义，则⎩⎨⎧4－x 2≥0x －1>0，即⎩⎪⎨⎪⎧－2≤x ≤2x >1，∴1＜x ≤2，即函数的定义域为(1,2]， 故选A.例2 (1)已知函数f (x )＝(23)|x |－a ，则函数f (x )的单调递增区间为________，单调递减区间为________．2．(2018·湖南衡阳期末)已知集合A ＝{x |log 12x >－1}，B ＝{x |2x >2}，则A ∪B ＝( )A.⎝⎛⎭⎫12，2B.⎝⎛⎭⎫12，＋∞ C ．(0，＋∞) D ．(0,2) 答案：C解析：由A ＝{x |log 12x >－1}＝{x |0<x <2}，B ＝{x |2x >2}＝⎩⎨⎧⎭⎬⎫x ⎪⎪x >12，则A ∪B ＝(0，＋∞)．故选C. 3．(2018·福建福州外国语学校期中)已知函数f (x )＝(m 2－m －1)x －5m －3是幂函数，且f (x )是(0，＋∞)上的增函数，则m 的值为( )A ．2B ．－1C ．－1或2D ．0 答案：B解析：因为函数f (x )＝(m 2－m －1)x －5m －3是幂函数，所以m 2－m －1＝1，即m 2－m －2＝0，解得m ＝2或m＝－1.又因为幂函数在(0，＋∞)上单调递增，所以－5m －3>0，即m <－35，所以m ＝－1，故选B.方法点拨：求有关幂函数的解析式，一般采用待定系数法，即设出解析式后，利用已知条件，求出待定系数．注意幂函数中自变量的系数为1.4．(2018·重庆第一中学一诊模拟)设a ＝213，b ＝log 43，c ＝log 85，则a ，b ，c 的大小关系是( ) A ．a >b >c B ．a >c >b [来源:学科网]C ．b >c >aD ．c >b >a [来源:学科网ZXXK] 答案：A解析：由指数函数的性质知a >1，由对数函数的性质得0<b <1,0<c <1.c 可化为log 235；b 可化为log 23，∵(35)6<(3)6，∴b >c ，∴a >b >c ，故选A.5．函数f (x )＝a x －1a(a >0，a ≠1)的图象可能是( )答案：D解析：当a >1时，将y ＝a x 的图象向下平移1a 个单位长度得f (x )＝a x －1a的图象，A ，B 都不符合；当0<a <1时，将y ＝a x 的图象向下平移1a 个单位长度得f (x )＝a x －1a 的图象，而1a大于1，故选D.6．若函数y ＝f (x )的定义域为[2,4]，则y ＝f (log 12x )的定义域是( )A.⎣⎡⎦⎤12，1 B ．[4,16] C.⎣⎡⎦⎤116，14 D ．[2,4] 答案：C解析：令log 12x ＝t ，则y ＝f (log 12x )＝f (t )，因为函数y ＝f (x )的定义域是[2,4]，所以y ＝f (t )的定义域是[2,4]，即2≤t ≤4，所以2≤log 12x ≤4，解得116≤x ≤14，所以y ＝f (log 12x )的定义域是⎣⎡⎦⎤116，14. 7．(2018·武汉二模)设函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x －7，x <0，x ，x ≥0，若f (a )<1，则实数a 的取值范围是( )A ．(－∞，－3)B ．(1，＋∞)C ．(－3,1)D ．(－∞，－3)∪(1，＋∞) 答案：C解析：通解 当a <0时，不等式f (a )<1为⎝⎛⎭⎫12a－7<1，即⎝⎛⎭⎫12a <8，即⎝⎛⎭⎫12a <⎝⎛⎭⎫12－3，因为0<12<1，所以a >－3，此时－3<a <0；当a ≥0时，不等式f (a )<1为a <1，所以0≤a <1.故a 的取值范围是(－3,1)，故选C.优解 取a ＝0，f (0)＝0<1，符合题意，排除A ，B ，D.8．(2018·怀化二模)已知函数f (n )＝log n ＋1(n ＋2)(n ∈N *)，定义使f (1)·f (2)·f (3)·…·f (k )为整数的k (k ∈N *)叫做企盼数，则在区间[1,2 016]内的企盼数的个数是( )A ．8B ．9C ．10D ．11 答案：B解析：因为函数f (n )＝log n ＋1(n ＋2)(n ∈N *)，所以f (1)＝log 23，f (2)＝log 34，…，f (k )＝log k ＋1(k ＋2)，所以f (1)·f (2)·f (3)·…·f (k )＝log 23·log 34·…·log k ＋1(k ＋2)＝log 2(k ＋2)，若f (1)·f (2)·f (3)·…·f (k )为整数，则k ＋2＝2m ，m ∈Z ，又k ∈[1,2 016]，所以k ∈{2,6,14,30,62,126,254,510,1 022}，故在区间[1,2 016]内的企盼的个数是9.二、填空题[来源:学科网]9．log 327－log 33＋(5－1)0－⎝⎛⎭⎫9412＋cos 4π3＝________. 答案：0解析：原式＝log 3(27÷3)＋1－32－12＝1＋1－32－12＝0.10．(2018·江西自主招生)方程log 3(1＋2·3x)＝x ＋1的解为________． 答案：0解析：由方程log 3(1＋2·3x )＝x ＋1可得1＋2·3x ＝3x ＋1，化简可得3x ＝1，故x ＝0.11．(2018·山西一模，13)已知函数f (x )＝x 2－m 是定义在区间[－3－m ，m 2－m ]上的奇函数，则f (m )＝________. 答案：－1解析：由题意得m 2－m ＝3＋m ，即m 2－2m －3＝0，∴m ＝3或m ＝－1.当m ＝3时，f (x )＝x －1，[－3－m ，m 2－m ]为[－6,6]，f (x )在x ＝0处无意义，故舍去．[来源:学科网] 三、解答题12．已知函数f (x )＝log 3mx 2＋8x ＋nx 2＋1的定义域为R ，值域为[]0，2，求m ，n 的值．解析：由y ＝f (x )＝log 3mx 2＋8x ＋n x 2＋1，得3y ＝mx 2＋8x ＋nx 2＋1，即()3y －m ·x2－8x ＋3y －n ＝0[来源:学.科.网Z.X.X.K] ∵x ∈R ，∴Δ＝64－4(3y －m )(3y －n )≥0，即32y －(m ＋n )·3y ＋mn －16≤0由0≤y ≤2，得1≤3y≤9，由根与系数的关系得⎩⎪⎨⎪⎧m ＋n ＝1＋9mn －16＝1×9，解得m ＝n ＝5.【课后强化巩固练习与方法总结】1．已知集合M ＝{}x |y ＝x －1，N ＝{x |y ＝log 2(2－x )}，则∁R (M ∩N )等于( ) A ．[1,2) B ．(－∞，1)∪[2，＋∞) C ．[0,1] D ．(－∞，0)∪[2，＋∞)2．已知a ＝23log 4.1，b ＝23log 2.7，c ＝⎝⎛⎭⎫123log 0.1，则( ) A ．a ＞b ＞c B ．b ＞a ＞c C ．a ＞c ＞bD ．c ＞a ＞b3．函数y ＝log 12(x 2－3x ＋2)的递增区间是( )A ．(－∞，1)B ．(2，＋∞)C ．(－∞，32)D ．(32，＋∞)学管签字：学管主任签字：。

幂函数、指数函数和对数函数对数及其运算法则教案第一章：幂函数1.1 幂函数的定义与性质学习幂函数的定义，了解幂函数的基本形式f(x) = x^a。

探讨幂函数的性质，包括奇偶性、单调性、周期性等。

1.2 幂函数的图像与性质绘制常见幂函数的图像，观察图像的特点。

分析幂函数的单调区间、极值等性质。

第二章：指数函数2.1 指数函数的定义与性质学习指数函数的定义，了解指数函数的基本形式f(x) = a^x。

探讨指数函数的性质，包括单调性、稳定性、特殊点等。

2.2 指数函数的图像与性质绘制常见指数函数的图像，观察图像的特点。

分析指数函数的单调性、渐近线等性质。

第三章：对数函数3.1 对数函数的定义与性质学习对数函数的定义，了解对数函数的基本形式f(x) = log_a(x)。

探讨对数函数的性质，包括单调性、反函数关系、对数规则等。

3.2 对数函数的图像与性质绘制常见对数函数的图像，观察图像的特点。

分析对数函数的单调性、渐近线等性质。

第四章：对数运算法则4.1 对数的基本运算法则学习对数的加法、减法、乘法、除法等基本运算法则。

探讨对数运算的性质，如对数的中项定律、对数的换底公式等。

4.2 对数的复合运算法则学习对数的复合运算，如对数的乘方、对数的开方等。

探讨复合运算的性质，如对数的乘方公式、对数的开方公式等。

第五章：对数函数的应用5.1 对数函数在求解方程中的应用学习使用对数函数求解指数方程、对数方程等。

探讨对数函数在求解方程时的性质，如对数函数的单调性、对数函数的零点等。

5.2 对数函数在解决实际问题中的应用学习使用对数函数解决实际问题，如人口增长、放射性衰变等。

探讨对数函数在解决实际问题时的应用方法和对数函数的近似计算等。

第六章：幂函数的应用6.1 幂函数在几何中的应用学习幂函数在几何中的作用，如计算体积、面积等。

探讨幂函数在几何问题中的解题方法。

6.2 幂函数在物理中的应用学习幂函数在物理中的作用，如温度、速度等。

幂函数、指数函数和对数函数对数及其运算法则教案一、教学目标知识与技能：1. 理解幂函数、指数函数的定义和性质。

2. 掌握对数的定义和性质，了解对数函数的图像和应用。

3. 掌握对数的运算法则，并能应用于实际问题中。

过程与方法：1. 通过实例和图形，培养学生的观察和分析能力，提高学生对幂函数、指数函数和对数函数的理解。

2. 通过小组讨论和探究活动，培养学生的合作和沟通能力，提高学生对对数运算法则的掌握。

情感态度与价值观：1. 培养学生对数学的兴趣和好奇心，激发学生对幂函数、指数函数和对数函数的学习热情。

2. 培养学生的耐心和细心，提高学生在解决实际问题中的数学应用能力。

二、教学内容第一节：幂函数1. 幂函数的定义和性质2. 幂函数的图像和应用第二节：指数函数1. 指数函数的定义和性质2. 指数函数的图像和应用第三节：对数函数1. 对数的定义和性质2. 对数函数的图像和应用第四节：对数的运算法则1. 对数的加法和减法法则2. 对数的乘法和除法法则3. 对数的幂法则三、教学重点与难点重点：1. 幂函数、指数函数和对数函数的定义和性质。

2. 对数的运算法则。

难点：1. 对数函数的图像和应用。

2. 对数的幂法则的理解和应用。

四、教学方法与手段教学方法：1. 讲授法：讲解幂函数、指数函数和对数函数的定义和性质。

2. 案例分析法：分析实际问题中的应用，展示对数函数的图像。

3. 小组讨论法：分组讨论对数的运算法则，促进学生之间的交流和合作。

教学手段：1. 多媒体课件：展示幂函数、指数函数和对数函数的图像和实例。

2. 练习题：提供练习题，帮助学生巩固所学知识和技能。

1. 课堂参与度：观察学生在课堂中的积极参与和提问情况，评价学生的学习兴趣和主动性。

2. 练习题完成情况：检查学生完成练习题的正确率和解题思路，评价学生的理解和应用能力。

3. 小组讨论报告：评估学生在小组讨论中的表现和合作能力，以及对数运算法则的理解和应用。

幂函数、指数函数和对数函数·对数及其运算法则·教案教学目标：1. 理解幂函数、指数函数和对数函数的定义及性质。

2. 掌握对数的定义及其运算法则。

3. 能够运用幂函数、指数函数和对数函数解决实际问题。

教学内容：第一章：幂函数1.1 幂函数的定义与性质1.2 幂函数图像的特点1.3 幂函数的应用第二章：指数函数2.1 指数函数的定义与性质2.2 指数函数图像的特点2.3 指数函数的应用第三章：对数函数3.1 对数的定义与性质3.2 对数函数图像的特点3.3 对数函数的应用第四章：对数及其运算法则4.1 对数的换底公式4.2 对数的运算法则4.3 对数函数的图像与性质第五章：实际问题中的应用5.1 利用幂函数、指数函数和对数函数解决实际问题5.2 练习题及解答教学方法：1. 采用讲授法，讲解幂函数、指数函数和对数函数的定义、性质及应用。

2. 利用数形结合法，引导学生观察函数图像，加深对函数性质的理解。

3. 通过例题和实际问题，培养学生的应用能力。

教学评估：1. 课堂提问，检查学生对幂函数、指数函数和对数函数的理解程度。

2. 布置课后作业，巩固所学知识。

3. 进行单元测试，评估学生的掌握情况。

教学资源：1. 教学PPT，展示幂函数、指数函数和对数函数的图像及性质。

2. 教材和辅导书，提供相关知识点的详细讲解和例题。

3. 网络资源，查阅实际问题中的应用案例。

教学时间安排：1. 第一章：2课时2. 第二章：2课时3. 第三章：2课时4. 第四章：2课时5. 第五章：1课时幂函数、指数函数和对数函数·对数及其运算法则·教案（续）教学内容：第六章：指数与对数的互化6.1 指数与对数的关系6.2 指数与对数的互化方法6.3 指数与对数互化在实际问题中的应用第七章：对数函数的图像与性质7.1 对数函数的图像特点7.2 对数函数的性质7.3 对数函数图像与性质的应用第八章：对数函数在实际问题中的应用8.1 对数函数解决生长、衰减问题8.2 对数函数在几何问题中的应用8.3 对数函数在其他领域的应用第九章：对数方程与对数不等式9.1 对数方程的解法9.2 对数不等式的解法9.3 对数方程与对数不等式的应用第十章：总结与拓展10.1 幂函数、指数函数和对数函数的总结10.2 数学思想与方法的拓展10.3 课后习题与思考题教学方法：1. 采用讲授法，讲解指数与对数的关系、互化方法及其应用。

幂函数、指数函数和对数函数·对数及其运算法则·教案教学目标：一、知识与技能：1. 理解幂函数、指数函数和对数函数的定义及其性质。

2. 掌握对数的定义及其运算法则。

3. 能够运用幂函数、指数函数和对数函数解决实际问题。

二、过程与方法：1. 通过实例探究幂函数、指数函数和对数函数的图象与性质。

2. 通过对数函数的图象和性质，理解对数及其运算法则。

3. 运用幂函数、指数函数和对数函数解决实际问题，提高数学建模能力。

三、情感态度与价值观：1. 培养对数学的兴趣和好奇心，感受数学的运用价值。

2. 培养学生的团队合作精神，提高学生的解决问题的能力。

教学重点与难点：重点：幂函数、指数函数和对数函数的定义及其性质；对数的定义及其运算法则。

难点：幂函数、指数函数和对数函数在实际问题中的应用。

教学过程：一、导入（5分钟）1. 复习幂函数、指数函数的定义及其性质。

2. 引导学生思考：幂函数、指数函数在实际生活中有哪些应用？二、新课讲解（15分钟）1. 讲解对数的定义：以2为底的对数表示为log2(x)，意义为2的几次方等于x。

2. 引导学生通过实例理解对数的意义。

3. 讲解对数的性质：对数的真数必须大于0；对数的底数必须不等于1；对数的相反数、对数的倒数、对数的乘积和除法等性质。

三、课堂练习（10分钟）1. 让学生独立完成练习题，巩固对数的定义及其性质。

2. 解答学生疑问，指导学生掌握对数的运算法则。

四、应用拓展（10分钟）1. 让学生举例说明幂函数、指数函数和对数函数在实际生活中的应用。

2. 引导学生运用幂函数、指数函数和对数函数解决实际问题。

五、课堂小结（5分钟）2. 强调对数的运算法则及其应用。

教学反思：本节课通过讲解幂函数、指数函数和对数函数的定义及其性质，让学生掌握对数的定义及其运算法则。

在教学过程中，注重引导学生思考实际生活中的应用，提高学生的数学建模能力。

通过课堂练习和应用拓展，巩固所学知识，提高学生的解决问题的能力。