2013年全国研究生数学建模竞赛D题918
- 格式:doc
- 大小:41.00 KB
- 文档页数:3


2013年全国研究生数学建模竞赛D 题空气中PM2.5问题的研究大气为地球上生命的繁衍与人类的发展提供了理想的环境。
它的状态和变化,直接影响着人类的生产、生活和生存。
空气质量问题始终是政府、环境保护部门和全国人民关注的热点问题。
2013年7月12日《中国新闻网》记者周锐报道:“2013年初以来,中国发生大范围持续雾霾天气。
据统计,受影响雾霾区域包括华北平原、黄淮、江淮、江汉、江南、华南北部等地区,受影响面积约占国土面积的1/4,受影响人口约6亿人”(中国国家发展和改革委员会(发改委)2013年7月11日公布在官方网站上的一份报告披露了上述信息,中新社北京7月11日电)。
对空气质量监测,预报和控制等问题,国家和地方政府均制定了相应政策、法规和管理办法。
2012年2月29日,环境保护部公布了新修订的《环境空气质量标准》 (GB3095—2012)[1],本次修订的主要内容:调整了环境空气功能区分类,将三类区并入二类区;增设了颗粒物(粒径小于等于2.5μm)浓度限值和臭氧8小时平均浓度限值;调整了颗粒物(粒径小于等于10μm)、二氧化氮、铅和苯并(a)芘等的浓度限值;调整了数据统计的有效性规定。
与新标准同步还实施了《环境空气质量指数(AQI)技术规定(试行) 》 (HJ633—2012)[2]。
新标准将分期实施,京津冀、长三角、珠三角等重点区域以及直辖市和省会城市已率先开始实施并发布AQI(Air Quality Index);今年113个环境保护重点城市和国家环保模范城市也已经实施;到2015年所有地级以上城市将开始实施;2016年1月1日,将在全国实施新标准。
上述规定中,启用空气质量指数AQI 作为空气质量监测指标,以代替原来的空气质量监测指标――空气污染指数API (Air Pollution Index)。
原监测指标API 为无量纲指数,它的分项监测指标为3个基本指标(二氧化硫2SO 、二氧化氮2NO 和可吸入颗粒物PM10)。


区名年年平均降水量年平均最高气温年平均最低气温年平均风速A2002 1.0520.38.44 6.21 A2003 2.2618.628.47 5.98 A2004 1.8420.118.56 6.14 A2005 1.5819.848.53 5.58 A2006 1.3420.319.33 5.43 A2007 1.3920.239.12 5.02 A2008 1.4320.038.85 4.9 A2009 2.0519.858.67 4.79 A2010 1.8219.558.83 4.76 A2011 1.5719.198.83 4.54区名年年平均降水量年平均最高气温年平均最低气温年平均风速B2002 1.4420.8210.5 6.1 B2003 2.8318.8510.24 5.28 B2004 2.2920.7710.75 5.33 B2005 2.3719.9210.61 5.18 B2006 1.7220.8911.71 5.42 B2007 1.9620.7911.99 5.08 B2008 1.4320.4411.69 4.95 B2009 1.820.3511.54 4.96 B2010 2.1920.4411.72 5.03 B2011 1.7119.5211.26 4.6区名年年平均降水量年平均最高气温年平均最低气温年平均风速C2002 1.5120.3210.07 5.96 C2003 3.1318.3710.01 6.28 C2004 2.119.810.57 6.22 C2005 1.5619.2810.33 5.78 C2006 1.4420.2411.36 5.56 C2007 1.4620.0511.18 5.46 C2008 1.5319.7910.4 5.39 C2009 1.6519.6910.62 5.17 C2010 1.5519.5710.49 5.3 C2011 2.419.0410.4 5.01区名年年平均降水量年平均最高气温年平均最低气温年平均风速D2002 2.421.1411.48 4.5 D2003 3.1319.5210.81 4.38 D2004 2.321.0811.27 4.34 D2005 2.9720.2410.92 4.07 D2006 1.8821.4111.97 4.14 D2007 2.0721.311.99 3.8 D2008 2.2920.811.53 3.64 D2009 2.4120.4211.91 3.65 D2010 3.3120.8111.89 3.81 D2011 2.120.5811.89 3.67区名年年平均降水量年平均最高气温年平均最低气温年平均风速E2002 1.6520.6910.47 4.28 E2003 3.7318.9110.11 4.28E2004 2.8920.4510.39 4.6 E2005 2.3119.710.04 4.3 E2006 1.7920.5610.9 4.14 E2007 2.2820.4110.84 4.08 E2008 2.2419.710.16 4.11 E2009 2.042010.17 3.98 E2010 2.2620.2610.33 4.14 E2011 2.3319.599.86 3.75区名年年平均降水量年平均最高气温年平均最低气温年平均风速F2002120.810.3 5.3 F2003 2.519.210 5.2 F2004220.510.4 5.3 F2005 1.719.910.45 F2006 1.520.911.35 F2007 1.220.911.2 4.7 F2008 1.620.510.8 4.9 F2009 1.520.310.7 4.9 F2010 1.820.410.9 4.8 F2011 1.719.610.4 4.6区名年年平均降水量年平均最高气温年平均最低气温年平均风速G2002 3.621.112.1 5.4 G2003419.611.2 5.3 G2004 2.921.412.1 5.5 G2005 3.920.111.8 4.9 G2006 2.921.212.5 4.9 G2007 4.221.412.9 4.7 G2008 3.720.712.2 4.7 G2009 2.620.412.2 4.7 G2010320.612.4 4.6 G2011 2.120.211.7 4.3区名年年平均降水量年平均最高气温年平均最低气温年平均风速H2002 1.6421.1411 5.1 H2003 2.6119.4910.29 5.03 H2004 2.120.9710.76 5.2 H2005 2.220.110.6 4.8 H2006221.211.4 4.7 H2007 1.821.211.6 4.6 H2008220.911.1 4.9 H2009 2.320.811.1 4.8 H2010 1.820.911.1 4.9 H2011 2.120.110.8 4.6区名年年平均降水量年平均最高气温年平均最低气温年平均风速I2002 1.921.411.6 3.9 I2003 3.819.511.2 3.4 I2004 2.921.412 3.2 I2005 2.820.411.7 2.7 I2006 2.321.412.5 2.8I2007 2.821.312.63 I2008 2.320.811.93 I2009 2.221.211.9 3.1 I2010 2.321.412 3.3 I2011 2.120.811.8 2.5区名年年平均降水量年平均最高气温年平均最低气温年平均风速J2002 2.521.111.8 4.6 J2003 4.119.511.1 4.5 J2004 2.221.311.6 4.6 J2005420.111.24 J2006 3.121.312 3.9 J2007 3.321.112.2 3.5 J2008 2.920.511.6 3.6 J2009 2.520.711.9 3.6 J2010 2.420.912 3.6 J2011220.411.7 3.1冰雹次数221110冰雹次数1111120冰雹次数1111111冰雹次数1111121冰雹次数111211冰雹次数11111112冰雹次数111111冰雹次数1121111冰雹次数1111210冰雹次数11111111。

2023年我国研究生数学建模竞赛D题专题一、选题背景2023年我国研究生数学建模竞赛是一项全国性的学术竞赛活动,旨在培养和锻炼研究生的数学建模能力,推动科学研究和创新发展。
本次竞赛D题的选题背景紧抠当前社会经济发展和科技进步的实际需求,旨在挑战参赛者的创新思维和综合应用能力,促进数学建模理论与实际问题的结合,推动数学科学的发展。
二、题目描述D题的题目是关于人口迁移模式和城市发展规划的研究。
随着城市化进程的加快和人口流动性的增强,人口迁移对城市发展和规划产生了深远影响。
本题要求参赛者运用数学模型、统计分析以及相关领域知识,研究城市人口迁移的规律和趋势,预测未来人口迁移的模式和规模,为城市规划和发展提供科学依据。
三、题目要求1. 分析当前城市人口迁移的主要模式和原因,包括城市间迁移、城市内部流动等。
2. 建立数学模型,考虑城市规模、经济发展水平、教育医疗资源、就业机会等因素,对人口迁移进行定量描述和预测。
3. 结合实际数据,对模型进行验证和调整,提高模型的准确性和可靠性。
4. 提出人口迁移对城市规划和发展的影响,以及可能的政策建议。
四、解题思路1. 了解当前城市人口迁移的主要模式和原因,包括人口流动的空间分布特征、人口流动的数量规模、人口流动的动态变化等。
2. 建立数学模型,对城市人口迁移进行定量分析和模拟,可以采用统计学方法、时空分析方法等。
3. 结合实际数据进行模型验证,对模型进行合理性和可行性测试,提高模型的适用性和普适性。
4. 提出人口迁移对城市规划和发展的影响,结合模型分析结果,给出相应的政策建议和发展方向。
五、参考资料1. 相关学术期刊和论文,了解国内外关于城市人口迁移的研究成果和方法。
2. 国家统计局等权威机构发布的有关城市人口迁移的统计数据和调查报告。
3. 城市规划和发展委员会的相关文件和政策,了解当前城市规划和发展的现状和趋势。
六、写作指南1. 在文章的概述部分,简要介绍城市人口迁移的背景和重要性,引出本题的研究意义和价值。
2013年全国研究生数学建模竞赛E 题中等收入定位与人口度量模型研究居民收入分配关系到广大民众的生活水平,分配公平程度是广泛关注的话题。
其中中等收入人口比重是反映收入分配格局的重要指标,这一人口比重越大,意味着收入分配结构越合理,称之为“橄榄型”收入分配格局。
在这种收入分配格局下,收入差距不大,社会消费旺盛,人民生活水平高,社会稳定。
一般经济发达国家都具有这种分配格局。
我国处于经济转型期,收入分配格局处于重要的调整期,“橄榄型”收入分配格局正处于形成阶段。
因此,监控收入分配格局的变化是经济社会发展的重要课题,例如需要回答,与前年比较,去年的收入分配格局改善了吗?改善了多少?可见实际上需要回答三个问题:什么是“橄榄型”收入分配格局?收入分配格局怎样的变化可以称之为改善?改善了多少?直观上,中间部分人口增加,则收入分配格局向好的方向转化。
于是基本问题回答什么是中间部分。
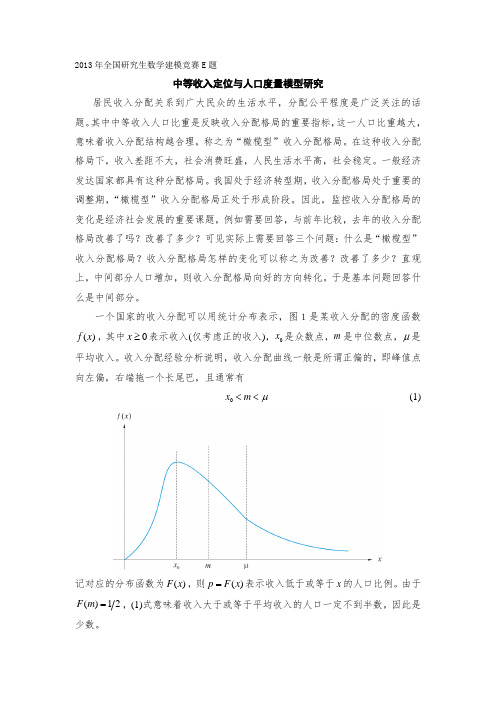
一个国家的收入分配可以用统计分布表示,图1是某收入分配的密度函数)(x f ,其中0≥x 表示收入(仅考虑正的收入),0x 是众数点,m 是中位数点,μ是平均收入。
收入分配经验分析说明,收入分配曲线一般是所谓正偏的,即峰值点向左偏,右端拖一个长尾巴,且通常有μ<<m x 0 (1)记对应的分布函数为)(x F ,则)(x F p =表示收入低于或等于x 的人口比例。
由于21)(=m F ,(1)式意味着收入大于或等于平均收入的人口一定不到半数,因此是少数。
记收入低于或等于x 的人口群体拥有收入占总收入的比例为)(p L ,则应有⎰=x t t tf p L 0d )(1)(μ,)(x F p = (2))(p L 称之为收入分配的洛伦兹曲线。
显然,如果)(1p L 与)(2p L 是两个不同收入分配的洛伦兹曲线,若对任何)1,0(∈p 都有)()(21p L p L ≥,则)(1p L 对应的收入分配显然更优,因为在)(1p L 中,任何低收入端人口拥有的总收入比例更大。
2013深圳夏令营数学建模承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完明白, 在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞赛规则的行为,我们将受到严肃处理.我们参赛选择的题号是(从题中选择一项填写): D 题所属学校:贵州民族大学参赛队员:1.姓名:2.姓名:3.姓名:指导教师或指导教师组负责人(打印并签名):2013深圳夏令营数学建模编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):自然灾害保险问题的研究摘要本文讨论了如何建立合理的自然灾害保险的问题,并建立了关于P省农业保险公司盈亏的简洁数学模型。
引入。
原理对于问题一,对于问题二,对于问题三,关键词:费率、线性回归、农业保险一、问题重述根据2013年3月5日《环球时报》转摘美国《商业周报》的相关报道,“在2012年全世界发生的10大自然灾害中,有4场是发生在中国。
包括3场严重的夏季洪涝灾和席卷苏鲁冀等沿海地区的台风‘达维’造成的灾害。
另外,还有很多地区遭受了严重干旱、冰雹等自然灾害,共造成290亿美元的损失,但通过投保由保险公司赔付的比例仅占总损失的4%左右,这个比例相对美国的自然灾害保险赔付率相差甚远。
”另据报道:“2013年3月20日发生在广东、广西等省部分地区的一场大风和冰雹灾害,造成直接经济损失达13亿多元。
”这个事实警示我们,中国需要重视和加强自然灾害保险的研究和实践,特别是针对严重自然灾害的保险体系建设和对策方案的研究,推动由政府主导的自然灾害政策性保险方案的实施。
公共自行车服务系统运行规律研究-----以浙江省温州市鹿城区为例摘要:根据浙江省温州市鹿城区公共自行车使用数据,基于公共自行车服务模式和使用规则,对公共自行车服务系统的运行规律从各个站点运行规律、借车人借车规律和高峰日系统的具体运行规律三个方面进行研究。
并基于所发现的规律对目前公共自行车服务系统的设置进行了评价,同时给出了提高系统效率的建议。
首先分别统计各站点20天中每天及累计的借车频次和还车频次。
结果显示,几乎所有站点在20天中的累计借车频次排序和还车频次排序大致相同。
另外也对每次用车时长的分布情况也进行了分析,发现用车时长主要集中在30分钟之内,约占用车量的90%;而用车时长在60分钟之内的用车量占总用车量的99%。
这与鹿城区公共自行车租赁收费标准(1小时内免费,超过1小时收费)相吻合。
以上现象也间接说明了政府制定的收费机制的有效性。
然后统计了20天中各天使用公共自行车的不同借车人数量,并统计了数据中出现过的每张借车卡累计借车次数的分布情况。
结果表明,20天中借车人数呈现明显的周期性波动,并且波动周期大约为7天。
而且波动量非常大,从最高峰第20天约20000个借车人到最低峰不到5000人。
还发现每张借车卡累计借车次数的分布情况如下:20天中55%的借车人借车次数不超过10次,35%的在10-30次之间,9%的在30次以上。
最后基于用车次数最多的第20天的数据对系统进行更为详细的分析。
发现借还车站点之间最长距离为32号站到45号站的距离,最短为73号站到115号站,99号站到150号站的距离。
借还车频次最高的站点分别为42号站点(770次)和56号站点(743次)。
两个站点借还车主要时间段相同,98.6%的借车在7:00到21:00之间,99.9%的还车在7:00到21:30之间。
发现两个站点运行规律的不同点有:56号站点比42号站点在早晨上班时的用车高峰更明显。
56号站点比45号站点用车时长在30分钟之内的多3.3%,说明还车高峰期人们会较快使用完自行车。
表错误!未找到引用源。
.1 单面印刷文字碎纸片(附件1:中文)复原后序号表位置 1 2 3 4 5 6 7 8 9 10 图片008 014 012 015 003 010 002 016 001 004 位置11 12 13 14 15 16 17 18 19图片005 009 013 018 011 007 017 000 006注:扩展名为.bmp,下同表错误!未找到引用源。
.2 单面印刷文字碎纸片(附件2:中文)复原后序号表位置 1 2 3 4 5 6 7 8 9 10 图片003 006 002 007 015 018 011 000 005 001 位置11 12 13 14 15 16 17 18 19图片009 013 010 008 012 014 017 016 004表4.3 单面印刷文字碎纸片(附件3:中文)复原后序号表表4.4 单面印刷文字碎纸片(附件4:英文)复原后序号表表4.6 双面印刷文字碎纸片(附件5:英文)复原后序号表2复原图见下页附录G主要算法程序%部分求解代码b=[];c=[];filename=cell(1,19);for i=0:18filename(i+1)={[sprintf('%03d',i) '.bmp']};a=imread(['附件2\\' filename{i+1}]);a=im2bw(a);b=[b a(:,72)]; %每片最后一列c=[c a(:,1)]; %每片第一列endminnonzero=[]; %匹配到最小的非0个数matchresult=[]; %匹配结果for k=1:19matindex=-1;minnonzero(k)=size(b,1);if size(nonzeros(b(:,k)),1)~=size(b(:,k),1) for i=1:19d=c(:,i)-b(:,k);nonzero=size(nonzeros(d),1);%for j=1:size(d,1)% if d(j)% nonzero=nonzero+1;% end%endif nonzero<minnonzero(k)minnonzero(k)=nonzero;matindex=i;endendelsematindex=0; %是纸张的两端endmatchresult(k)=matindex;endmatchresult=matchresult-1;newfile=cell(1,19);index=-1;for i=19:-1:1for j=1:19%matchresult(j)if matchresult(j)==indexnewfile(i)=filename(j);index=j-1;break;endendendj=1:19;%xlswrite('result.xls',filename,'第一问','B6');%xlswrite('result.xls',matchresult,'第一问','B7'); %xlswrite('result.xls',minnonzero,'第一问','B8'); xlswrite('result.xls',j,'第一问','B4');xlswrite('result.xls',newfile,'第一问','B5');a=[];for i=0:18a=[a imread(['附件2\\' newfile{i+1}])]; endimshow(a)。
2013年全国研究生数学建模竞赛D 题
空气中PM2.5问题的研究
大气为地球上生命的繁衍与人类的发展提供了理想的环境。
它的状态和变化,直
接影响着人类的生产、生活和生存。
空气质量问题始终是政府、环境保护部门和全国人民关注的热点问题。
2013年7月12日《中国新闻网》记者周锐报道:“2013年初以来,中国发生大
范围持续雾霾天气。
据统计,受影响雾霾区域包括华北平原、黄·淮、江淮、江汉、江南、华南北部等地区,受影响面积约占国土面积的1/4,受影响人口约6亿人”(中国国家发展和改革委员会(发改委)2013年7月11日公布在官方网站上的一份报告披露了上述信息,中新社北京7月11日电)。
对空气质量监测,预报和控制等问题,国家和地方政府均制定了相应政策、法规
和管理办法。
2012年2月29日,环境保护部公布了新修订的《环境空气质量标准》 (GB3095—2012)[1],本次修订的主要内容:调整了环境空气功能区分类,将三类区并入二类区;增设了颗粒物(粒径小于等于2.5μm)浓度限值和臭氧8小时平均浓度限值;调整了颗粒物(粒径小于等于10μm)、二氧化氮、铅和苯并(a)芘等的浓度限值;调整了数据统计的有效性规定。
与新标准同步还实施了《环境空气质量指数(AQI)技术规定(试行) 》 (HJ633—2012)[2]。
新标准将分期实施,京津冀、长三角、珠三角等重点区域以及直辖市和省会城市
已率先开始实施并发布AQI(Air Quality Index);今年113个环境保护重点城市和国家环保模范城市也已经实施;到2015年所有地级以上城市将开始实施;2016年1月1日,将在全国实施新标准。
上述规定中,启用空气质量指数AQI 作为空气质量监测指标,以代替原来的空气
质量监测指标――空气污染指数API (Air Pollution Index)。
原监测指标API 为无量纲指数,它的分项监测指标为3个基本指标(二氧化硫2SO 、二氧化氮2NO 和可吸
入颗粒物PM10)。
AQI 也是无量纲指数,它的分项监测指标为6个基本监测指标(二氧化硫2SO 、二氧化氮2NO 、可吸入颗粒物PM10、细颗粒物PM2.5、臭氧3O 和一氧化碳CO 等6 项)。
新标准中,首次将产生灰霾的主要因素——对人类健康危害极大的细颗粒物PM2.5的浓度指标作为空气质量监测指标 [2]。
新监测标准的发布和实施,将会对空气质量的监测,改善生存环境起到重要的作用。
由于细颗粒物PM2.5进入公众视线的时间还很短,在学术界也是新课题,尤其是
对细颗粒物PM2.5及相关的因素的统计数据还太少,对细颗粒物PM2.5的客观规律也了解得很不够。
但是相关研究人员绝不能因此而放慢前进的脚步,不能“等”数据,
因为全国人民等不起。
我们必须千方百计利用现有的数据开展研究,同时新课题、探索性研究、“灰箱问题”也有可能成为数学建模爱好者的用武之地。
请研究以下问题。
一、PM2.5的相关因素分析
PM2.5的形成机理和过程比较复杂,主要来源有自然源(植物花粉和孢子、土壤扬尘、海盐、森林火灾、火山爆发等)和人为源(燃烧燃料、工业生产过程排放、交通运输排放等),可以分为一次颗粒物(即由排放源直接排放到大气中的颗粒物)和二次颗粒物(即通过与大气组成成分发生化学反应后生成的颗粒物)。
PM2.5的成分主要由水溶性离子、颗粒有机物和微量元素等组成。
有一种研究认为,AQI监测指标中
的二氧化硫(SO
2 ),二氧化氮(NO
2
),一氧化碳(CO)是在一定环境条件下形成PM2.5
前的主要气态物体。
请依据附件1或附件2中的数据或自行采集数据,利用或建立适当的数学模型,对AQI中6个基本监测指标的相关与独立性进行定量分析,尤其是对其中PM2.5(含量)与其它5项分指标及其对应污染物(含量)之间的相关性及其关系进行分析。
如果你们进而发现AQI基本监测指标以外的、与PM2.5强相关的(可监测的)成分要素,请陈述你们的方法、定量分析结果、数据及来源。
二、PM2.5的分布与演变及应急处理
请依据附件2、附件3中的数据或自行采集某地区的数据,通过数学建模探索完成以下研究:
1、描述该地区内PM2.5的时空分布及其规律,并结合环境保护部新修订的《环境空气质量标准》分区进行污染评估。
2、建立能够刻画该地区PM2.5的发生和演变(扩散与衰减等)规律的数学模型,合理考虑风力、湿度等天气和季节因素的影响,并利用该地区的数据进行定量与定性分析。
3、假设该地区某监测点处的PM2.5的浓度突然增至数倍,且延续数小时,请建立针对这种突发情形的污染扩散预测与评估方法。
并以该地区PM2.5监测数据最高的一天为例,在全地区PM2.5浓度最高点处的浓度增至2倍,持续2小时,利用你们的模型进行预测评估,给出重度污染和可能安全区域。
4、采用适当方法检验你们模型和方法的合理性,并根据已有研究成果探索PM2.5 的成因、演变等一般性规律。
注:有关PM2.5的监测数据目前还很不充分。
附件2、附件3中的数据是我们迄今为止找到的唯一大型城市的连续一段时间且比较齐全的PM2.5的相关数据,非常珍贵。
有可能的话,希望你们能够自行收集更充分的数据,研究相关问题。
三、空气质量的控制管理
地方环境管理部门关心的重要问题之一是,为建设良好的人居环境,利用有限财力,制定本地区空气质量首要污染物PM2.5的减排治污可行规划。
数据1所在地区的环境保护部门考虑治污达标的紧迫性和可行性,在未来五年内,拟采取综合治理和专项治理相结合的逐年达到治理目标的方案。
请考虑以下问题:
μ),要求未来五
1、该地区目前PM2.5的年平均浓度估计为280(单位为3
g
m
/
年内逐年减少PM2.5的年平均浓度,最终达到年终平均浓度统计指标35(单位为3
μ),请给出合理的治理计划,即给出每年的全年年终平均治理指标。
g
m
/
2、据估算,综合治理费用,每减少一个PM2.5浓度单位,当年需投入一个费用单位(百万元),专项治理投入费用是当年所减少 PM2.5浓度平方的0.005倍(百万元)。
请你为数据1所在地区设计有效的专项治理计划,使得既达到预定PM2.5减排计划,同时使经费投入较为合理,要求你给出五年投入总经费和逐年经费投入预算计划,并论述该方案的合理性。
附件1. 数据1.(武汉市一个监测点数据:2013.01.01-2013.08.26)
附件2.数据2.(西安市13个监测点数据:2013.01.01-2013.04.26)或从以下链接获取最新数据:/sxmpcp_qt.asp?lb=%D6%CA%C1%BF%C8%D5%B1%A8
/空气质量日报历史数据>>
附件3. 数据3.1.(西安地区气象数据1(2013.4.1-2013.8.28))
数据3.2.(西安地区气象数据2(2011.1.1-2013.4.28))
附件4. AQI与API 的空气质量指数检测标准
附件5. 使用Google地图测量两点之间的平面距离的方法
附件6. 西安市13个监测点位置的平面示意图
参考文献
[1]环境空气质量标准, 中华人民共和国国家标准,GB 3095-2012
[2] 环境空气质量指数(AQI)技术规定(试行):中华人民共和国国家环境保护标准,
HJ 633-2012
[3] 中华人民共和国环境保护部,环境保护标准网站:。