当前位置：文档之家 › 大学物理 平面简谐波的波函数

大学物理 平面简谐波的波函数

  • 格式：ppt
  • 大小：796.00 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

10-02 平面简谐波的波函数

10-02 平面简谐波的波函数

u
8m C B 5m 9m D
oA
x
1)以 A 为坐标原点,写出波动方程 ) 为坐标原点,
A = 3×10 m T = 0.5s = 0
2
2
λ = uT = 10 m
x y = (3 × 10 ) cos(4π t )m 5
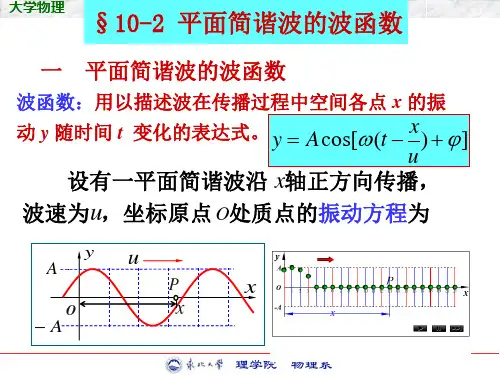
10 – 2 平面简谐波的波函数
第十章 波动
2)以 B 为坐标原点,写出波动方程(首先要知道 点的振动方程) ) 为坐标原点,写出波动方程(首先要知道B点的振动方程 点的振动方程)
( 0 .01cm -1 ) x 2 ] = 2 π
λ = x2 x1 = 200 cm
周期为相位传播一个波长所需的时间 周期为相位传播一个波长所需的时间
π [(2.50s-1 )t1 (0.01cm-1 ) x1 ] = π [(2.50s-1 )t2 (0.01cm-1 ) x2 ]
x2 x1 = λ = 200 cm
第十章 波动
y(x,t) = Acos(ωt kx +)
质元的振动速度, 质元的振动速度,加速度
t x y(x,t) = Acos[2 π( ) +] T λ
角波数
k= 2π
y x v = = ωAsin[ω(t ) +] t u 2 y x 2 a = 2 = ω Acos[ω(t ) +] t u
y = A cos(ω t
O
2π
t=0 x=0
y ω
λ
x +)
π = 2
A
y y = 0, v = >0 t
t x π y = (1 . 0 m) cos[ 2 π ( ) ] 2.0s 2.0 m 2

10-2平面简谐波的波函数

10-2平面简谐波的波函数

x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
yO Acost
yO表示质点O在 t时刻离开平衡位置的距离.
考察波线上P点(坐标x), P点比O点的振
动t 落Δ后t 时刻t 的ux,位P移点，在由t此时得刻的位移是O点在
y A
u
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
y
u
A
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
故P点的振动方程（波动方程）为：
y
yo
(t
t)
A cos[ (t
x) u
]
对波动方程的各种形式，应着重从
物理意义上去理解从形式上看：波动是波形的传播.
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
大学物理 §§1100--22 平平面简面谐波简的谐波函波数 的波函数
一 平面简谐波的波函数
波函数：用以描述波在传播过程中空间各点 x 的振
动 y 随时间 t 变化的表达式。 y Acos[(t x) ]
u
设有一平面简谐波沿 x轴正方向传播，
波速为u，坐标原点 O处质点的振动方程为
y A
u
P
uu
Acos[(t x ) ( x0 )]
理学u院 物理u系
大学物理
§10-2 平面简谐波的波函数
例4 一平面简谐波以速度 u 20 m s-1 沿直线传播，波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t); ( y, t单位分别为m，s).

5-2平面简谐波的波动方程详解

5-2平面简谐波的波动方程详解

u 沿 x 轴正向 u 沿 x 轴负向
第5章 机械波
5–2 平面简谐波的波动方程 平面简谐波波函数的其它形式
大学物理学 （第3版）
t y A cos[2 π( T
y A cos[2 t
y A cos[ 2
2 x
x ) 0 ] λ

0 ]

(ut x) 0 ] A cos[k (ut x) 0 ]
x y A cos (t ) (沿x轴负向传播) u
第5章 机械波
5–2 平面简谐波的波动方程 如果原点的
大学物理学 （第3版）
A
O
y
u

初相位不为零
x
x 0, 0 0 A
点 O 振动方程
y0 A cos(t 0 )
波 函 数
x y A cos[ (t ) 0 ] u x y A cos[ (t ) 0 ] u
2 y G 2 y 2 t x2 2 y E 2 y 2 t x 2
G为切变模量
固体内弹性平面纵波
E为杨氏模量
张紧柔软线绳上传播横波
2 y T 2 y 2 t x 2
T为线绳所受张力，为线密度:单位长度线绳的质量
第5章 机械波
5–2 平面简谐波的波动方程 2、波速 固体中弹性横波 固体中弹性纵波 张紧软绳中横波
x0 x0 2 π u λ
y ( x, t ) y ( x, t T ) （波具有时间的周期性）
第5章 机械波
5–2 平面简谐波的波动方程
大学物理学 （第3版）
波线上各点的简谐运动图
第5章 机械波
5–2 平面简谐波的波动方程

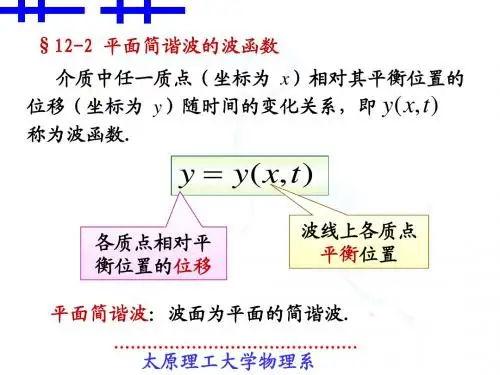
§12-2平面简谐波的波函数

§12-2平面简谐波的波函数

x2 − x1 −1 u= = 250 cm ⋅ s t 2 − t1
轴正方向传播， 例2 一平面简谐波沿 O x 轴正方向传播，已知振 幅 A = 1.0m T = 2 . 0 s λ = 2.0m .在 t = 0 时坐 标原点处的质点位于平衡位置沿 O y 轴正方向运 动 .求 1）波函数 解:写出波函数的标准式
振动向右传播 滞后的时间
x ∆t = u
t 时刻点 P 的运动
=
t-x/u时刻点 的运动 时刻点O 时刻点
P点振动方程
yP
t
= yO
t−x u
x = A cos[ω (t − ) + ϕ0 ] u
点选取的任意性，得波函数即上式。 由P点选取的任意性，得波函数即上式。 太原理工大学物理系
方法之二
相位落后法
8m 5m 9m
−2
λ = 10 m
C B o A D 点 C 的相位比点 A 超前 AC −2 yC = 3 × 10 cos[4 π t + 2 π ]
x
点的坐标x＝ 带入波函数 将D点的坐标 ＝9m带入波函数 点的坐标
−2
λ 13 −2 = 3 × 10 cos[4 π t + π] 5
t 9 y D = 3 ×10 cos[2 π( − )](m) 0.5 10
12§12-2 平面简谐波的波函数 介质中任一质点（ 介质中任一质点（坐标为 x）相对其平衡位置的 ） 位移（ 位移（坐标为 y）随时间的变化关系，即 y ( x, t ) ）随时间的变化关系， 称为波函数. 称为波函数.
y = y ( x, t )
各质点相对平 衡位置的位移 衡位置的位移 波线上各质点 平衡位置 平衡位置

11-2 平面简谐波的波函数

11-2 平面简谐波的波函数

-
x u
)=
Acos ω
t
-
x u
+
0
上页 下页 返回 退出
P处质点在时刻t 的位移为：
yP (t) =
Acos ω
t
-
x u
+
0
波 函 数
因此，波线上任一点在任一时刻的位移都能 由上式给出。此即所求的沿x 轴正方向前进 的平面简谐波的波函数。
沿x轴负方向传播的平面简谐波的波函数：
上页 下页 返回 退出
2
1
2
x2 x1
2
x
x、t 都变化:
实线：t1 时刻波形；虚线：t2 时刻波形
y
u
o
x
x x
上页 下页 返回 退出
当t=t1时，y
A
cos
t1
x u
0
当t=
t1+Δt时，y
A
cos
t1
t
x u
0
在t1和t1+Δt时刻，对应的位移用x1和x2表示，则
y(t1)
A cos
t1
x1 u
0
y
A cos
2
(
t
mx
)
0
y Acos(t mkx 0 )
k 2 角波数
y
y
A cos(t
Aei
(t
mx u
)0
m2 x
i (t
Ae
0
mk ) u
)
上页 下页 返回 退出
波动表式的意义：
x 一定：令x=x1，则质点位移y 仅是时间t 的函数。
即
y
A
cos

平面简谐波波函数

平面简谐波波函数
大学物理
波动学基础
第2讲 平面简谐波波函数
平面简谐波波函数
平面简谐波波函数
在均匀的、无吸收的介质中, 波源作简谐运动而形成 平面简谐波.
如何描述一维平面简谐波即建立波动表达式?其所表 示的物理意义是什么?
平面简谐波波函数
(一)波函数的建立 y = y(x，t )
任选参考点 O 为 x 轴的坐标原点, O 点处 质点的简谐运动方程 为
y
∆x
O x1
x2 x
y
=
A cos ω⎜⎛ t1 ⎝
−
x u
⎞ ⎟ ⎠
相位差为
∆ϕ
= ϕ1
−ϕ2
=
2π⎜⎛ t ⎝T
−
x1 λ
⎞ ⎟
−
2π⎜⎛
t
⎠ ⎝T
−
x2 λ
⎞ ⎟ ⎠
=
2π
x2
− λ
x1
波程差 ∆x = x2 − x1 相位差和波程差的关系： ∆ϕ = 2π ∆x
λ
平面简谐波波函数
(3)当 t , x 都变时, y = y(x, t), 表示所有质元在任意时刻 的位移情况.
解: 由图得
A = 2.5cm = 0.025m，λ = 40m，
T = 4s，ω = 2π = π s−1，u = λ = 10m ⋅s−1
y (cm )
T2
Tuv
20
5
x(m )
OP
波动表达式为
y
=
A
cos
⎡ ⎢ω ⎣
⎜⎛ t ⎝
−
x u
⎞ ⎟ ⎠
+
⎤ ϕ⎥
⎦
代入 t = 0, x = 0 , y = 0 ⇒ cosϕ = 0

平面简谐波的波函数表达式

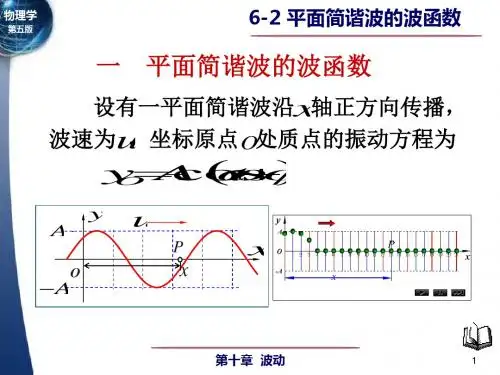
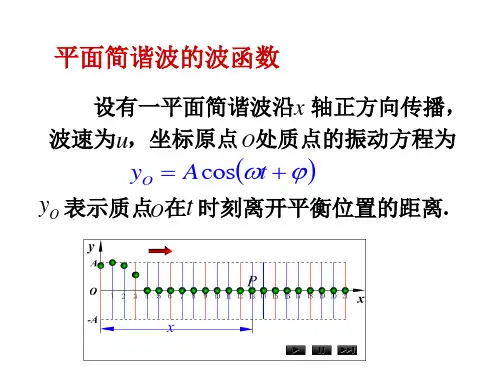
平面简谐波的波函数表达式
平面简谐波是一种特殊的波形，它的波函数表达式可以用以下公式表示：
y = A sin(ωt + φ)
其中，y表示波的振幅，A表示最大振幅，ω表示角频率，t表示时间，φ表示初相位。

平面简谐波是一种具有周期性的波形，它的周期T可以用以下公式计算：
T = 2π/ω
角频率ω是一个常数，它表示单位时间内波形的变化次数。

因此，角
频率越大，波形变化的速度就越快，周期就越短。

初相位φ是一个常数，它表示波形在t=0时的相位。

不同的初相位会导致波形的相位差异，从而产生不同的波形。

平面简谐波的波函数表达式可以用于描述许多物理现象，例如声波、
电磁波等。

在声学中，平面简谐波可以用于描述声音的振动，而在电磁学中，平面简谐波可以用于描述电磁场的振动。

平面简谐波的振幅和角频率是两个重要的参数，它们可以影响波形的形状和特性。

振幅越大，波形的振动幅度就越大，而角频率越大，波形的变化速度就越快。

平面简谐波还具有一些重要的性质，例如叠加原理和相位差。

叠加原理指出，当两个或多个平面简谐波叠加在一起时，它们的振幅可以相加，从而形成一个新的波形。

相位差指出，当两个平面简谐波的相位差为0时，它们的振幅可以相加，而当相位差为π时，它们的振幅可以相消。

总之，平面简谐波是一种重要的波形，它的波函数表达式可以用于描述许多物理现象。

了解平面简谐波的特性和性质，可以帮助我们更好地理解和应用它们。

大学物理平面简谐波的波函数精选精品文档


u
1m 0
λ10m 8 m 5 m 9 m
C
B oA
Dx
第十章 波动
21
物理学
第五版
选择进入下一节：
本章目录
6-1 机械波的几个概念
6-2 平面简谐波的波函数
6-3 波的能量 能流密度 6-4 惠更斯原理 波的衍射和干涉
6-5 驻波
6-6 多普勒效应
第十章 波动
22

x






A cos


t

2πx




第十章 波动
4
物理学
第五版
6-2 平面简谐波的波函数
波函数
yAcos(t[x)]
u
质点的振动速度，加速度
v y A si n (t [x)]
t
u
a 2 t2 y 2A co (ts[u x)]
第五版
6-2 平面简谐波的波函数
(3) x0.5m处质点的振动规律并作图
y1.0co2π s([t x)π] 2.0 2.0 2
x0.5m处质点的振动方程
ycoπst[π](m)
y
y/m
3
3
1.0
*
4O
2
0 2* 1.0 *4 2.0 * t / s
1 -1.0*1
*
x0.5m处质点的振动曲线
第十章 波动
15
物理学
第五版
6-2 平面简谐波的波函数
例2 一平面简谐波以速度u20ms-1
沿直线传播，波线上点 A 的简谐运动方 程
yA31 0 2co4π st)(; ( y, t单位分别为m，s).

大学本科大学物理第5次课 波函数


os2π
t T
x
A c ost
2πx
第十章 波动
5
物理学
第五版
10-6 多普勒效应
波函数
y Acos[(t x) ]
u
质点的振动速度，加速度
v y Asin[(t x) ]
t
u
a
2 y t 2
2
A cos[ (t
x) u
]
第十章 波动
6
物理学
第五版
10-6 多普勒效应
二 波函数的物理含义
y
y/m
3
3
1.0
*
4O
2
0 2* 1.0 *4 2.0 * t / s
1 -1.0*1
*
x 0.5 m 处质点的振动曲线
第十章 波动
16
物理学
第五版
10-6 多普勒效应
例2 一平面简谐波以速度u 20 m s-1
沿直线传播，波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t); ( y, t单位分别为m，s).
yu
O
x
第十章 波动
10
物理学
第五版
10-6 多普勒效应
4 沿 x轴方向传播的波动方程
如图，设 O 点振动方程为
yO A cost
P点振动比O点超前了 Δt x u
y
u
A
P
x
O
x
A
第十章 波动
11
物理学
第五版
10-6 多普勒效应
故P点的振动方程（波动方程）为：
y
yo (t
t)
A c os [ (t
点C 的相位比点A 超前

平面简谐波的波函数

课堂练习 图示为 t = 1s 时的波形曲线，求波动方程。
提示 关键：求解原点o处质元初位相 o ！
(t 0)
o
2
A
y
y(m)
0.08 m/s
0.04
(t 1)
t
25
(1
0)
2
5
o
2
2
5
9
10
o
P
0.20
x (m)
t 1s
答案： y
0.04 cos [2
5
(t
x ) 0.08
9 ]
10
(
t
x u
)
o
]
(t
x u
)
o
(t
t
x
x u
)
o
x ut
y
u
☻波速即为相位传播速度 o
( 相速 ) 。
☻行波或前进波。
x
ut
·7 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
三、微分形式的平面波波动方程
对一般的平面波：
xoy系：y f (x, t) xoy系： y f (x)
y
A
cos
[
(t
x u
)
o
]
波函数亦称 波动方程 。
ut
Ao y(0 ,t )
Δt Ax
(x,t)
o
y(x,t) y
t o
·3 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
波动方程 的几种标准形式： y
y
A
cos
[
(t
x u
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
此刻的波形.
y Acos[2 π x (2π t )] T
y(x,t) y(x ,t)（波具有空间的周期性）
波程差
x21 x2 x1
12
1 2
2π
x2 x1
2π
x21
2π
x
回目录
3若
x, t 均变化，波函数表示波形沿传播方向的运动情况（行波）.
yu
t 时刻
x
O
x
t t 时刻
xx
x 0.5处m质点的振动方程
y 1.0cos(π t π)m
y
y/m
3
1.0
3*
2
4
4O
2
0
* 1.0
* 2.0
*
t /s
1 -1.0* 1
*
x 0.5 m 处质点的振动曲线
回目录
例2 一平面简谐波以速度
沿u直线传20播m,波线/ s上点 A 的简谐运动方
程
. yA 310 2 cos(4 π t)m
y Acos式(中Bt Cx)
A, B, C 为正常数，求波长、波速、波传播方向上相距为 的两点间的相位差.
d
y Acos(Bt Cx)
y Acos2 π ( t x )
T
2π
C
T 2π B
u B
TC
2π d dC回目录
二 波函数的物理意义
y Acos[(t x) ] Acos[2 π( t x ) ]
u
8m 5m 9m
C
B oA
Dx
1）以 A 为坐标原点，写出波函数
两种方法：时间推迟法和相位落后法
y 3102 cos[4 π(t x )]m 20
回目录
2）以 B 为坐标原点，写出波函数
yA 310 2 cos(4 π t)m
u
8m 5m 9m
C oB A
Dx
yB
3102
cos(4 π t
2π
AB )m
yB 310 2 cos(4 π t π)m y 3102 cos[4 π(t x ) π]m
20
回目录
3）写出传播方向上点C、点D 的简谐运动方程
u
8m
yA 3102 cos(4 π t)m
5m 9m
10m
C
B oA
Dx
点 C 的相位比点 A 超前
yC
3102 cos(4 π t 2 π AC)m
v y Asin[(t x) ]
t
u
a
2 y t 2
2 Acos[(t
x) u
]
回目录
讨论
1）给出下列波函数所表示的波的传播方向和
点的初相位.
x0
tx
y Acos2π ( )
T
(向x 轴正向传播
y Acos (t x) ( x 向 轴负向传播
u
, π) , π)
2）平面简谐波的波函数为
y A
u
不为零
O
x 0, 0 A
x
点 O 振动方程
yO Acos(t )
波 y Acos[ (t x) ] u沿 x轴正向
函 数
u
y Acos[ (t x) ] u沿 x轴负向
u
回目录
➢ 平面简谐波波函数的其它形式
y(x,t) Acos[2 π( t x) ]
Tλ
➢ 质点的振动速度，加速度
.T求，
2.0s
2.0m . 在
时坐标原点处的质点位于平衡位置
1）波函数
解 写出波函数的标准式
O
y
A
y Acos[2π( t x ) ] T
t0 x0
y 0, v y 0
π
2
t
y 1.0cos[2π( t x ) π]m 2.0 2.0 2
回目录
2） x 0.处5质m点的振动规律并作图 . y 1.0 cos[2π( t x ) π ]m 2.0 2.0 2
一 平面简谐波的波函数
介质中任一质点（坐标为 x）相对其平衡位置的位移（坐标为 y）随时间的变
化关系，即
称为波函数.
y( x, t )
y y(x,t)
各质点相对平衡位置的 位移
波线上各质点平衡位置
➢ 简谐波：在均匀的、无吸收的介质中，波源作简谐运动时，在介质中所形成 的波.
➢ 平面简谐波：波面为平面的简谐波.
yP (t)
y0 (t
t)
A c os (t
x 回)目录 u
➢ 波函数
A y u
y Acos(t x)
u
相位落后法
Ox
A
P
*
x 点 O 振动方程
yo Acost
x 0, 0
P O 点 比点 落后的相位
p
O
2π
x
2π
x Tu
x u
P 点 振动方程
yp
A cos (t
x) u
回目录
如果原点的初相位
1.6 π
C
D
2π
CD
2π
22 10
4.4 π
回目录
1.一平面简谐波的波动方程为y = 0.1cos(3t－x+)(SI) t = 0 时的波形曲线如图所示，则 (A) O点的振幅为－0.1m . (B) 波长为3m . (C) a、b两点间相位差为/2 . (D) 波速为9m/s .
y (m)
u
3102
c
os(4
π
t
13
π)m
点 D 的相位落后于点 A
5
yD
3102 cos(4πt 2π AD)m
3
102
c
os
(4
π
t
9
π)m
5
回目录
4）分别求出 BC cos(4 π t)m
u
8m 5m 9m
10m
C
B oA
Dx
B
C
2 π
BC
2 π 8 10
回目录
讨论：如图简谐波以余弦函 数表示，求 O、a、b、c 各点振 动初相位.
t =0
y
A
(π ~ π )
A
O
y
A
O
y
o π
a
π 2
Oa
A
O
O A
u
b c
A
y
y
t=T/4
x
b 0
c
π 回2目录
例1 一平面简谐波沿 O x 轴正方向传播， 已知振
t 0 幅
沿
OAy 轴正1方.0，向m运动
0.1
·
·
O· －0.1
ab
x (m)
回目录
2. 一平面简谐波表达式为y=－0.05sin(t－2x) (SI), 则该波的频率ν(Hz),波速u(m/s)及波线上各点振动 的振幅A(m)依次为 (A) 1/2, 1/2, －0.05 . (B) 1/2, 1 , －0.05 . (C) 2, 2 , 0.05 . (D) 1/2, 1/2, 0.05 .
回目录
各种不同的简谐波
简谐波 1 简谐波 2
合成 复杂波
合成 分解
复杂波
回目录
u x 以速度 沿
轴正向传播的平面简谐波 . 令原点O 的初相为零，其 振动方程
yO Acost
时间推迟方 点O 的振动状态
法
yO Acost
t-x/u时刻点O 的运动
t x u
t 时刻点 P 的运动
点P
P 点 振动方程
u
T
x 1 当 固定时， 波函数表示该点的简谐运动方程，并给出该点与点 O
振动的相位差.
x 2 π x
u
λ
y(x,t) y(x,t T ) （波具有时间的周期性）
回目录
波线上各点的简谐运动图
回目录
y Acos[(t x) ] Acos[2 π( t x ) ]
u
T
t 2 当 一定时，波函数表示该时刻波线上各点相对其平衡位置的位移，即