平面简谐波的能量
- 格式:pdf
- 大小:1.25 MB
- 文档页数:14

第一章1.在下列运动中,加速度保持不变的运动是:()答案:抛体运动2.速度的大小可以用来表示。
()答案:对3.当质点作抛体运动时其an和at是不断变化的,因此也是不断变化的.()答案:错4.一质点作曲线运动,则下列说法正确的是:()(1)(2)(3)(4)答案:(3)(4)正确5.一运动质点在某瞬时位于矢径的端点处,其加速度大小为:( ) 答案:第二章1.下列说法中,哪一个是正确的:()答案:物体的加速度方向总是沿着它所受的合外力方向。
2.对于作曲线运动的物体,以下几种说法中哪一种是正确的:()答案:法向加速度必不为零(拐点处除外);3.轻型飞机连同驾驶员总质量为m,飞机以v0的速率在水平跑道上着陆后,驾驶员开始制动,若阻力与时间成正比,比例系数为b,则飞行t时间后飞机的速率为:()答案:;4.加速度是由速度的大小和方向共同决定的。
()答案:对5.牛顿第一定律定性地指明了,惯性参照系中力是改变质点运动状态的唯一原因。
()答案:对第三章1.冲击摆是一种测定子弹速率的装置。
木块的质量为m2,被悬挂在细绳的下端。
有一质量为m1的子弹以速率v1沿水平方向射入木块中后,子弹与木块将一起摆至高度为h处。
则此子弹射入木块前的速率为:()答案:;2.质量的物体,在坐标原点处从静止出发在水平面内沿x轴运动,其所受合力方向与运动方向相同,合力大小为,则物体在开始运动的2m内,合力所做的功为: ( )答案:3.质量的物体,在坐标原点处从静止出发在水平面内沿x轴运动,其所受合力方向与运动方向相同,合力大小为,则物体在开始运动的2m内,合力所做的功可求出,当时,其速率为:( )答案:4.质量的物体,在坐标原点处从静止出发在水平面内沿X轴运动,其所受合力方向与运动方向相同,合力大小为,则物体在开始运动的3内,合力所做的功为:()答案:36(SI)5.质量的物体,在坐标原点处从静止出发在水平面内沿X轴运动,其所受合力方向与运动方向相同,合力大小为,则物体在开始运动的3内,合力所做的功可求,则当时,其速率为:()答案:12(SI)6.牛顿第二定律与动量定理本质上是一致的,牛顿第二定律要求合外力与加速度一一对应的过程关系;动量定理更加注重状态结果。


1.《医用物理学》教学要求骨骼肌、平滑肌的收缩、张应力、正应力、杨氏模量、2.理想流体、连续性方程、伯努利方程3.黏性液体的流动状态4.收尾速度、斯托克斯定律5.附加压强6.表面张力系数、表面活性物质7.毛细现象8.热力学第一定律9.热力学第一定律在等值过程中的应用(等压、等温)10.热力学第二定律11.电动势、稳恒电流12.一段含源电路的欧姆定律13.基尔霍夫定律应用14.复杂电路:电桥电路15.简谐振动的初相位16.平面简谐波的能量、特征量(波长、频率、周期等)17.光程、相干光18.惠更斯原理19.双缝干涉20.单缝衍射21.光的偏振22.X射线的产生条件23.X射线的衰减24.标识X射线的产生原理25.X射线的短波极限26.放射性活度27.放射性原子核衰变方式28.半衰期、衰变常数、平均寿命29.辐射防护医用物理学练习题练习一1-1.物体受张应力的作用而发生断裂时,该张应力称为( D )A .范性B .延展性C .抗压强度D .抗张强度1-2平滑肌在某些适宜的刺激下就会发生( A )A .自发的节律性收缩B .等宽收缩C .不自主收缩D .等级收缩1-3.骨骼肌主动收缩所产生的张力和被动伸长所产生的张力的关系是( C )A .不等于B .小于C .大于D .近似等于1-4.头骨的抗压强度为×108Pa ,如果质量为1kg 的重物,竖直砸到人的头上,设重物与头骨的作用时间为1×10-3s ,作用面积为0.4cm 2,问重物离头顶至少多高下落才会砸破人的头骨?解: 头骨的抗压强度N 108.6104.0107.1348⨯=⨯⨯⨯==-S F σ根据机械能守恒可得 221v m mgh =因此有 g h 22v = 根据动量定理有v m t F =⋅ 求v 代入上式得1-5.说明正应力、正应变和杨氏模量的定义以及它们之间的关系。
答:垂直作用在物体某截面上的内力F 与该截面面积S 的比值,称为物体在此截面处所受的正应力。




机械波
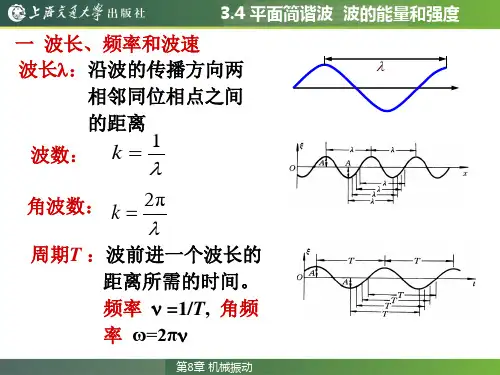
1、波速、波长及周期的关系
μ=λ/T
μ=λν
注:波的周期T(或频率ν)是波源的周期(或频率),与传播波的媒质无关。
波速μ取决于传播媒质的性质
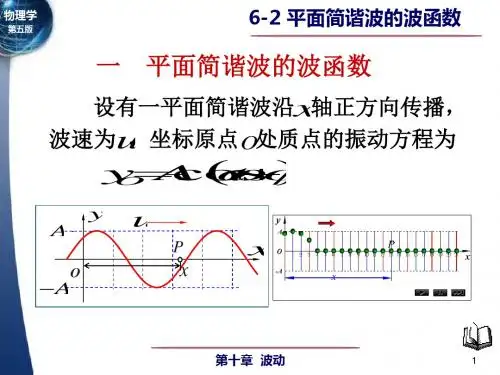
2、振动方程和波动方程
(1)振动方程(正向传播)
y=Acosω(t-x/μ) (基本形式)
y=Acos2π(νt- x/λ)
y=Acos2π(t/T- x/λ)
注:A-振幅,恒为正;ω-角频率,ω=2π/T=2πν
(2)波动方程
y=Acos[ω(t-x/μ)+Ф] (正向传播)
y=Acos[ω(t+x/μ)+Ф] (反向传播)
3、平面简谐波的能量
最大位移处:动能、势能及总能量均为零
平衡位置:动能、势能及总能量均达到最大
4、波的干涉
1、合振动振幅:A=
2、分振动相位差:
3、波程差:
4、驻波
5、概念:
特征:
波动光学
1、光的干涉
1)杨氏双缝干涉
相邻明纹或相邻暗纹中心的间距(条纹间距)
2)明、暗干涉条纹条件
3)光程、光程差、相位差
4)薄膜干涉(劈尖干涉)
5)牛顿环
2、光的衍射
1)明暗条纹
2)条纹间距
3)特征
3、光的偏振
1)马吕斯定律。

第一章复习一、描述运动的物理量1、描写质点运动的基本物理量(线量)(1)位置矢量:k z j y i x r++=。
(2)位移12r r r-=∆,注意与路程的区别。
(3)速度:dt r d v =,平均速度:t r v ∆∆= ,速率:||||dtrd dt dS v v ===(4)加速度直角坐标系:22dtrd dt v d a ==;平面自然坐标系:n v dt dv n a a a n ρτττττ2+=+= 2、描写刚体定轴转动的基本物理量(角量) (1)角位置θ(2)角位移12θθθ-=∆ (3)角速度dtd θω=(4)角加速度22dtd dt d θωβ==3、圆周运动角量与线量的关系:θ∆=∆R s ; R v ω=; R dtdva βτ==; R R v a n 22ω==。
二、运动方程1、直角坐标系中的运动方程:)(t r r=;2、定轴转动刚体的运动方程:)(t θθ=;3、自然坐标系中的运动方程:)(t s s =;三、轨迹方程四、可能出现的题型:1、根据运动方程求:位移,路程,速度,平均速度,速率,加速度,平均加速度等。
注意判别所求的物理量是矢量还是标量!2、根据加速度或速度以及初始条件求运动方程等。
可能用到的方法:图形面积法;矢量积分法(注意式中各物理量之间的变换,如:dxvdvdx dx dt dv dt dv a ===)。
3、根据运动方程求轨迹方程——消去运动方程中的时间即可。
4、利用匀变速直线运动公式或匀变速转动公式求解有关量。
匀变速直线运动公式:恒量=a ,at v v +=0,20021at t v x x ++=,)(20202x x a v v -=-匀变速转动公式:恒量=β,t βωω+=0,20021t t βωθθ++=,)(20202θθβωω-=-5、n a a a ,,τ的求解(1)直角坐标系中一般可由22dt r d dt v d a ==求出总加速度a,再根据||||dtr d v v ==求出速率,再根据dtdv a =τ求τa ,然后根据22n a a a +=τ求n a ,进而求曲率半径。

平面简谐波的势能和动能简谐波是一类具有定常性质的波,它是瞬变电磁场的特殊表现形式,也是许多物理现象的基础,可以在自由空间或介质中传播。
简谐波具有电场、磁场和动能。
平面简谐波是一种特殊的简谐波,它由两个恒定方向的空间动量组成,这种波在空间传播时,每个点上的动量和电场都是一致的,因此它有一个特殊的势能和动能。
本文尝试研究平面简谐波的势能和动能的具体形式,并将它们与其他类型的波的动能和势能相比较。
二、势能平面简谐波的势能是由电场和磁场共同作用的结果,它可以用来表示波的总体能量分布,而它也是一个满足某种条件的函数。
具体来说,平面简谐波的势能可以表示为:P(x)=E(x)B(x)其中,x是一个位置向量,E和B分别表示电场和磁场的强度场。
三、动能动能是物体伴随运动产生的能量,它可以表示为物体的动量。
平面简谐波的动能是由一个有限的空间频率组成的,也就是说,动能是流体运动的频率,并且满足一定的波动方程。
根据物理意义,动能是流体在不同位置上的动量之和,可以表示为:K=∫P(x)dx其中,P(x)表示动能的强度场,x是位置向量,K表示总动能。
四、与其他类型波动能势能的比较其他类型波与平面简谐波有所不同,但它们的势能和动能具有相同的性质。
例如,柱面波的势能为:P(x,y)=E (x,y)B (x,y)而柱面波的动能可以表示为:K=∫∫P(x,y)dxdydz可以看出,与平面简谐波相比,柱面波的势能和动能的计算方式有所不同,但是它们的物理意义是一样的。
此外,现实中的很多波也具有类似的性质,它们的势能和动能也是一样的。
五、结论平面简谐波具有电场、磁场和动能,其势能和动能可以用不同的方法来表示,但它们的本质是一样的,与其他类型波也具有同样的性质。
描述平面简谐波概念介绍平面简谐波是一种特殊的波动现象,在许多自然和物理现象中都能观察到。
它是一种周期性的振动,沿着固定的方向传播,并且其振动方向与传播方向垂直。
平面简谐波具有一些独特的性质,深入了解这些性质能够帮助我们更好地理解波动现象的本质。
平面简谐波的定义平面简谐波是一种在时间和空间中都是周期性的波动。
它可以用数学公式来描述,通常表示为:y(x,t)=A⋅sin(kx−ωt+ϕ)在这个公式中,y是波的振幅,A是最大振幅;x是波的位置,t是时间,k是波数,表示波的空间频率;ω是角频率,表示波的时间频率;ϕ是相位,描述波动的起始位置。
平面简谐波的特点平面简谐波具有以下几个重要的特点:1. 周期性平面简谐波是周期性的,即在空间和时间上呈现出一定的重复性。
在任意时刻和位置上的波形都与之前的波形相似。
2. 定向性平面简谐波沿着固定的方向传播,其振动方向和传播方向垂直。
这意味着在波的传播过程中,波的能量在空间中沿着直线扩展。
3. 纯净性平面简谐波由一个频率确定的正弦函数组成,没有其他频率的分量。
这意味着波的频率是唯一确定的,没有任何杂散的频率成分。
4. 叠加原理平面简谐波具有良好的叠加原理。
多个平面简谐波可以在同一空间中叠加,并按照各自的振幅和相位叠加成一个新的平面简谐波。
平面简谐波的应用领域平面简谐波的概念和性质在物理学和工程领域有广泛的应用。
以下是一些常见的应用领域:1. 光学在光学中,平面简谐波被用来描述光的传播和干涉现象。
光是一种电磁波,可以用平面简谐波的概念来解释光的行为。
例如,光的干涉现象可以通过将多个平面简谐波叠加而成。
2. 声学在声学领域,平面简谐波被用来描述声波的传播和共鸣现象。
声波是一种机械波,可以用平面简谐波的概念来描述声波的振动和传播特性。
3. 信号处理在信号处理中,平面简谐波被广泛用来分析和合成信号。
通过将信号拆解为多个简谐波的叠加,可以更好地理解信号的频谱特性和时域特性,从而进行信号处理和调制。
一、平面简谐波的概念平面简谐波是一种特殊的波动现象,它具有特定的波动方程和波动特性。
简谐波的振幅随时间以正弦或余弦函数变化,具有周期性和频率性,是物理学中常见的一种波动形式。
二、平面简谐波的波动方程1. 时间域的波动方程在时间域内,平面简谐波的波动方程可以表示为:\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中,y表示波动的位移,A表示振幅,k表示波数,ω表示角频率,φ表示初相位。
2. 空间域的波动方程在空间域内,平面简谐波的波动方程可以表示为:\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中,y表示波动的位移,A表示振幅,k表示波数,ω表示角频率,φ表示初相位。
3. 复数形式的波动方程在复数形式下,平面简谐波的波动方程可以表示为:\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中,y表示波动的位移,A表示振幅,k表示波数,ω表示角频率,φ表示初相位。
三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的,都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。
它们之间通过变量的不同而具有不同的物理意义,但是描述的是同一种波动现象。
2. 复数形式的波动方程和实数形式的波动方程在复数形式下,简谐波的波动方程可以更加简洁地描述,通过复数的指数函数形式可以很方便地进行波动的运算和分析。
复数形式的波动方程和实数形式的波动方程是等价的,可以相互转化,但在不同的数学和物理背景下有着不同的应用优势。
四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式,广泛应用于物理学、工程学、生物学等领域。
它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值,可以用来描述和分析各种复杂的波动现象。
5.4 平面简谐波的能量简谐振动是指物体沿某一方向做相同的周期性运动。
在平面简谐波中,物体振动沿着平面的方向上,振动方程通常为y=A*sin(ωt±φ),其中A为振动的振幅,ω为角频率,t为时间,φ为初相位。
平面简谐波的能量可以从能量守恒定律和能量密度推导出来。
首先,从能量守恒定律来看,能量在物理学中是守恒的,只能从一种形式转化为另一种形式。
在平面简谐波中,能量的来源是振动体的动能和势能。
当振动体进行简谐振动时,动能和势能交替转化,它们的总和是恒定的。
在一个振动周期内,动能和势能各占一半,因此平面简谐波的总能量为:E=1/2*A²*m*ω²其中,A为振动的振幅,m为物体的质量,ω为角频率。
其次,从能量密度的角度来看,平面简谐波的能量密度可以写成:其中,ρ为介质的密度,v为平面波的速度。
根据波动方程,平面波的速度可以表示为v=ω/k,其中k为波数。
将v的表达式代入能量密度公式中,可得:u=1/2*ρ*(ω/k)²再将k的表达式k=2π/λ带入,得到:由于平面简谐波存在一个振动平面,因此其能量的密度在振动平面上的值最大。
对于由正弦函数表示的平面简谐波,其能量密度的最大值为:最后,由于平面简谐波在空间中是无限延伸的,因此其能量密度是密集分布的。
可以将平面简谐波所占据的空间划分为许多小立方体,每个小立方体能够存储的能量就是它的体积乘以能量密度。
总能量可以由所有小立方体内存储的能量相加得到。
综上,平面简谐波的能量可以由振动体的动能和势能的总和或者能量密度推导得到。
它的能量密度在振动平面上最大,并且在空间中密集分布。
探究平面简谐波质元的动能和势能平面简谐波质元是物理学中非常常见的一个概念,掌握它的运动规律以及动能和势能的关系对于解决许多问题都非常有帮助。
本文将从以下几个方面进行讲解:
1.平面简谐波的概念
平面简谐波是指在平面上呈现周期性的波,它可以用简单的正弦函数表达。
2.平面简谐波质元的概念
平面简谐波质元是指一个小质点按照平面简谐波运动规律运动的情况,它可以用一个简单的模型来描述。
3.平面简谐波质元的动能
平面简谐波质元的动能可以用公式 1/2*m*v^2 表示,其中m为质元的质量,v为质元在运动过程中的速度。
4.平面简谐波质元的势能
平面简谐波质元的势能可以用公式 1/2*k*x^2 表示,其中k为弹性系数,x为质元在运动过程中的位移。
5.动能和势能的关系
平面简谐波质元的总能量为动能加势能,根据上述公式可以得出
动能与势能之间的关系为动能=势能,这是根据平面简谐波的运动规律
所得出的结论。
总之,学习了平面简谐波质元的运动规律以及动能和势能的关系,可以帮助我们更好地理解物理学中的很多问题,也有利于我们更好地
应用这些知识进行科学研究、工程实践等方面的活动。
大学物理
波动学基础
第4讲平面简谐波的能量
平面简谐波的能量
在波的传播过程中, 介质中各质元的能量如何变化?遵循怎样的规律?
平面简谐波的能量
波动的过程是能量传播的过程.
介质中各质点在各自平衡位置附近振动动能
介质间相互作用产生弹性形变势能
一、平面简谐波传播时媒质中体积元的能量
(一)能量
设平面简谐波在密度为ρ的弹性介质中沿 x 正方向传
播: ϕ = 0
⎟
⎠
⎞
⎜⎝⎛−=u x t A y ωcos 在 x 处取体积元 ΔV ,
质量为
V
x S m ∆==∆ρρd
当波传到此 ΔV 时, 有
⎟
⎠
⎞⎜⎝⎛−−=∂∂=u x t A t y ωωsin v 所以体积元动能为
()()⎟
⎠
⎞⎜⎝⎛−∆=∆=∆u x t A V m E ωωρ2
222k sin 2121v 经推导(略), 体积元弹性形变势能也为
()⎟
⎠
⎞⎜⎝⎛−∆=∆u x t A V E ωωρ2
22p sin 21
体积元的总能量为
()⎟
⎠⎞⎜⎝
⎛
−∆=∆+∆=∆u x t A V E E E ωωρ2
2
2
p
k sin (1)能量的传播 (2)
(2)周期性的变化
(二)能量变化同相位
形变最大、振速最大(势能最大、动能最大)
形变最小、振速为零
(势能为零、动能为零)
O
x
y
a
b
(三)振动与波动中能量变化的区别
振动: 能量守恒
波动: 能量传播过程
——时大时小, 不守恒 ——
(一)能量密度
单位体积内波的能量————
能量密度 w :()⎟
⎠
⎞⎜⎝⎛−=∆∆==u x t A V E t x ωωρ222sin ,w w 能量密度的平均值:
2
202
1d 1ω
ρA t T T ==∫w w 机械波的能量与振幅平方, 频率平方以及介质密度成
正比.
二、波的能量密度 能流密度
(二)能流和能流密度
能流: 单位时间内垂直于波线方向流过某一面积的能量.
uS
P w =平均能流:
uS
P w = 能流密度: 在单位时间内垂直于波线方向的单位面积
上通过的平均波的能量.
S
P I =
()u S
uS I ⋅=⋅=w w (1)大小:
(2)方向:
(3)单位:2
m
W −⋅(4)能流密度也称为波的强度。
能流密度为矢量, 其方向为波速的方向.
u A I 222
1ωρ=即
(三)球面波(点波源激发)
2
211I r I r :: 单位时间内穿过这两个球
形面的总平均能量分别为
2
2
2
12
144I r I r ππ 以点O 为中心, r 1, r 2为半径, 作两个同心球形波面, 则
1
r O
2
r
因为无吸收, 由能量守恒定律得
2
2212144I
r I r ππ=所以21
2221r
r I I =即1
221r r A A =
则C
Ar r A r A ====L 2211即
r
C A =
C 为 r =1 时该处的振幅, 则球面波的波函数为
⎥
⎦
⎤⎢⎣⎡+⎟⎠⎞⎜⎝⎛−=ϕωu r t r C
y cos
解:
ωλπ
2=
=T T u Q π
2ωλ=∴u S
P w π
2ωλ=uS
P w = 例题 在截面积为 S 的圆管中, 有一列平面简谐波, 其波
动的表达式为
管中波的平均能量密度为 , , 则通过截面 S 的平均能流是多少?)
π2cos(λ
ωx
t A y −=w and。