平面简谐波方程
- 格式:pptx
- 大小:369.84 KB
- 文档页数:6

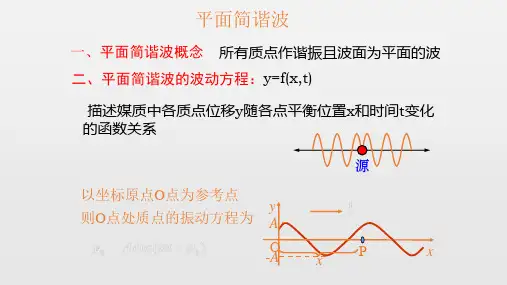
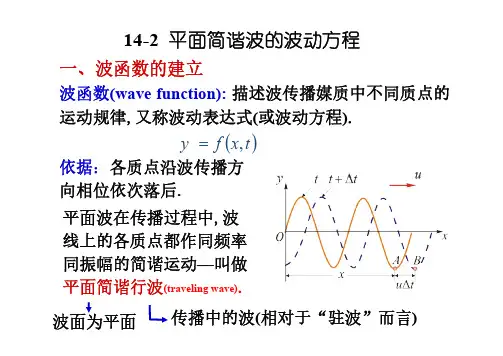

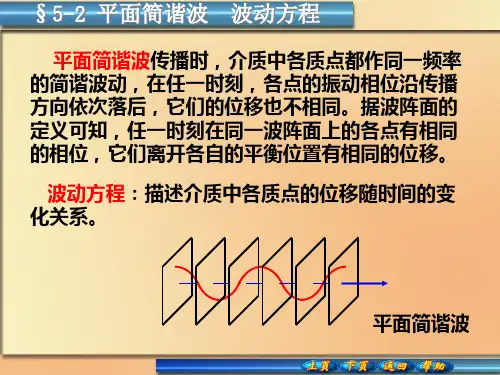
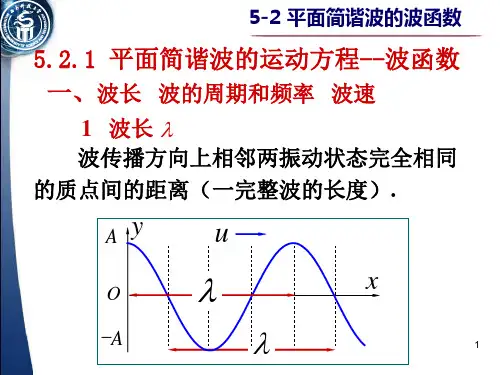

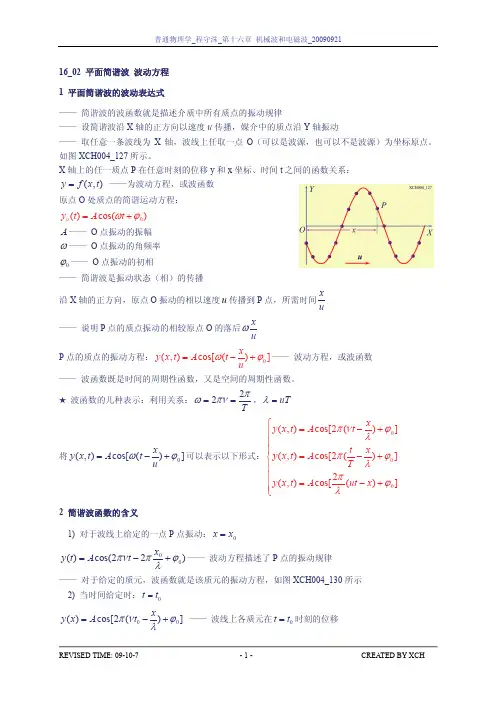
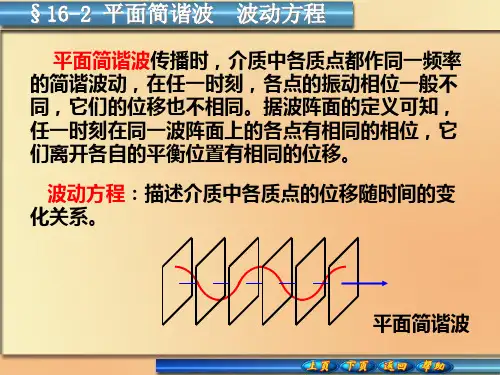


一、平面简谐波的概念平面简谐波是一种特殊的波动现象,它具有特定的波动方程和波动特性。
简谐波的振幅随时间以正弦或余弦函数变化,具有周期性和频率性,是物理学中常见的一种波动形式。
二、平面简谐波的波动方程1. 时间域的波动方程在时间域内,平面简谐波的波动方程可以表示为:\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中,y表示波动的位移,A表示振幅,k表示波数,ω表示角频率,φ表示初相位。
2. 空间域的波动方程在空间域内,平面简谐波的波动方程可以表示为:\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中,y表示波动的位移,A表示振幅,k表示波数,ω表示角频率,φ表示初相位。
3. 复数形式的波动方程在复数形式下,平面简谐波的波动方程可以表示为:\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中,y表示波动的位移,A表示振幅,k表示波数,ω表示角频率,φ表示初相位。
三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的,都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。
它们之间通过变量的不同而具有不同的物理意义,但是描述的是同一种波动现象。
2. 复数形式的波动方程和实数形式的波动方程在复数形式下,简谐波的波动方程可以更加简洁地描述,通过复数的指数函数形式可以很方便地进行波动的运算和分析。
复数形式的波动方程和实数形式的波动方程是等价的,可以相互转化,但在不同的数学和物理背景下有着不同的应用优势。
四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式,广泛应用于物理学、工程学、生物学等领域。
它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值,可以用来描述和分析各种复杂的波动现象。