下载文档原格式
习题8-1. 沿一平面简谐波的波线上，有相距的两质点与，点振动相位比点落后，已知振动周期为，求波长和波速。
解：根据题意，对于A、B两点，而相位和波长之间又满足这样的关系：代入数据，可得：波长λ=24m。
又已知T=2s，所以波速u=λ/T=12m/s 8-2．已知一平面波沿x轴正向传播，距坐标原点为处点的振动式为，波速为，求:（1）平面波的波动式；（2）若波沿x轴负向传播，波动式又如何?解：（1）根据题意，距坐标原点为处点是坐标原点的振动状态传过来的，其O点振动状态传到p点需用，也就是说t 时刻p处质点的振动状态重复时刻O处质点的振动状态。
换而言之，O处质点的振动状态相当于时刻p处质点的振动状态，则O点的振动方程为：波动方程为：（2）若波沿x轴负向传播， O处质点的振动状态相当于时刻p处质点的振动状态，则O 点的振动方程为：波动方程为：8-3. 一平面简谐波在空间传播，如图所示，已知点的振动规律为，试写出：（1）该平面简谐波的表达式；（2）点的振动表达式（点位于点右方处）。
解：（1）仿照上题的思路，根据题意，点的振动规律为，它的振动是O点传过来的，所以O点的振动方程为：那么该平面简谐波的表达式为：（2）B点的振动表达式可直接将坐标，代入波动方程：也可以根据B点的振动经过时间传给A点的思路来做。
8-4. 已知一沿x正方向传播的平面余弦波，时的波形如图所示，且周期为.（1）写出点的振动表达式；（2）写出该波的波动表达式；（3）写出点的振动表达式；（4）写出点离点的距离。
解：由图可知A=0.1m，λ=0.4m，由题知T= 2s，ω=2π/T=π，而u=λ/T=0.2m/s。
波动方程为：y=0.1cos［π(t-x/0.2)+Ф0］m 关键在于确定O点的初始相位。
（1）由上式可知：O点的相位也可写成：φ=πt+Ф0由图形可知：时y０=-A/2，v０＜0，∴此时的φ=2π／3，将此条件代入，所以：所以点的振动表达式y=0.1cos［πt+π/3］m（2）波动方程为：y=0.1cos［π(t-x/0.2)+π/3］m（3）点的振动表达式确定方法与O点相似由上式可知：A点的相位也可写成：φ=πt+ФA0由图形可知：时y０=0，v０>0，∴此时的φ=-π／2，将此条件代入，所以：所以A点的振动表达式y=0.1cos［πt-5π/6］m（4）将A点的坐标代入波动方程，可得到A的振动方程，与（3）结果相同，所以： y=0.1cos ［π(t-x/0.2)+π/3］= 0.1cos［πt-5π/6］可得到：8-5. 一平面简谐波以速度沿x轴负方向传播。
第八章 波动【例题精选】例8-1 如图，一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播，已知A 点的振动方程为 t y π⨯=-4c o s 1032(SI)． (1) 以A 点为坐标原点写出波的表达式；(2) 以距A 点5 m 处的B 点为坐标原点，写出波的表达式．解：(1) 坐标为x 点的振动相位为 )]/([4u x t t +π=+φω )]/([4u x t +π=)]20/([4x t +π=波的表达式为 )]20/([4cos 1032x t y +π⨯=- (SI)(2) 以B 点为坐标原点，则坐标为x 点的振动相位为 ]205[4-+π='+x t t φω (SI) 波的表达式为 ])20(4cos[1032π-+π⨯=-xt y (SI) 例8-2已知波长为λ 的平面简谐波沿x 轴负方向传播．x = λ /4处质点的振动方程为ut A y ⋅π=λ2cos(SI)(1) 写出该平面简谐波的表达式． (2) 画出t = T 时刻的波形图．解：(1) 如图A ，取波线上任一点P ，其坐标设为x ，由波的传播特性，P 点的振动落后于λ /4处质点的振动．波的表达式 )]4(22cos[x utA y -π-π=λλλ)222cos(x ut A λλπ+π-π= (SI) (2) t = T 时的波形和 t = 0时波形一样． t = 0时)22cos(x A y λπ+π-=)22cos(π-π=x A λ 按上述方程画的波形图见图B ．例8-3 某质点作简谐振动，周期为2 s ，振幅为0.06 m ，t = 0 时刻，质点恰好处在负向最大位移处，求：(1) 该质点的振动方程； (2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；(3) 该波的波长．解：(1) 振动方程 )22c o s (06.00π+π=ty )c o s (06.0π+π=t (SI) (2) 波动表达式 ])/(cos[06.0π+-π=u x t y ])21(cos[06.0π+-π=x t (SI)(3) 波长 4==uT λ mABxuOxPxλ/4 u图A例8-4 一平面简谐波沿Ox 轴正向传播，波动表达式为 ]4/)/(cos[π+-=u x t A y ω，则 x 1 = L 1处质点的振动方程是 ； x 2 = -L 2 处质点的振动和x 1 = L 1 处质点的振动的相位差为 φ2 - φ1 = ． ]4/)/(cos[11π+-=u L t A y ωuL L )(21+ω例8-5一平面简谐波的表达式为 )37.0125cos(025.0x t y -= (SI)，其波速u = ；波长λ = ．338 m/s 17.0 m例8-6 已知一平面简谐波的表达式为 )cos(bx at A -，（a 、b 均为正值常量），则波长为 ；波沿x轴传播的速度为 ．2π / b a /b例8-7 一平面简谐波的表达式为 )/(2c o sλνx t A y -π=．在t = 1 /ν 时刻，x 1 = 3λ /4与x 2 = λ /4二点处质元速度之比是 (A) -1． (B)31． (C) 1． (D) 3． [ A ] 例8-8 沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线如图所示，设波速u = 0.5 m/s ． 求：原点O 的振动方程． 解：由图，λ = 2 m ， 又 ∵u = 0.5 m/s ，∴ ν = 1 /4 Hz ， T = 4 s ．题图中t = 2 s =T 21．t = 0时，波形比题图中的波形倒退λ21，见图．此时O 点位移y 0 = 0（过平衡位置）且朝y 轴负方向运动，∴ π=21φ )2121c o s (5.0π+π=t y (SI) 例8-9 一平面简谐波沿x 轴正向传播，波的振幅A = 10 cm ，波的角频率ω = 7π rad/s.当t = 1.0 s 时，x = 10cm 处的a 质点正通过其平衡位置向y 轴负方向运动，而x = 20 cm 处的b 质点正通过y = 5.0 cm 点向y 轴正方向运动．设该波波长λ >10 cm ，求该平面波的表达式． 解：设平面简谐波的波长为λ，坐标原点处质点振动初相为φ，则波的表达式可写成 )/27c o s(1.0φλ+π-π=x t y (SI) t = 1 s 时 0])/1.0(27cos[1.0=+π-π=φλy因此时a 质点向y 轴负方向运动，故 π=+π-π21)/1.0(27φλ ① b 质点正通过y = 0.05 m 处向y 轴正方向运动，应有05.0])/2.0(27cos[1.0=+π-π=φλy且 π-=+π-π31)/2.0(27φλ ②由①、②两式联立得 λ = 0.24 m 3/17π-=φx (m)y (m) 0u0.5 12t = 0 -1∴ 该平面简谐波的表达式为 ]31712.07cos[1.0π-π-π=x t y (SI) 例8-10 图示一简谐波在t = 0时刻与t = T /4时刻（T 为周期）的波形图，则o处质点振动的初始相位为 ；x 1处质点的振动方程为 ．π /2 )22cos(1π-π=t T A y x 例8-11 图所示为一平面简谐波在t = 0 时刻的波形图，设此简谐波的频率为250Hz ，且此时质点P 的运动方向向下，求：(1) 该波的表达式；(2) 在距原点O 为100 m 处质点的振动方程与振动速度表达式．解：(1) 由P 点的运动方向，可判定该波向左传播．原点O 处质点，t = 0 时φcos 2/2A A =, 0sin 0<-=φωA v所以 4/π=φ O 处振动方程为 )41500c o s (0π+π=t A y (SI) 由图可判定波长λ = 200 m ，故波动表达式为]41)200250(2cos[π++π=x t A y (SI) (2) 距O 点100 m 处质点的振动方程是 )45500cos(1π+π=t A y振动速度表达式是 )45500cos(500π+ππ-=t A v (SI)例8-12 一平面简谐波在弹性媒质中传播时，某一时刻媒质中某质元在负的最大位移处，则它的能量是 (A) 动能为零，势能最大． (B) 动能为零，势能为零．(C) 动能最大，势能最大． (D) 动能最大，势能为零． [ B ] 例8-13 设入射波的表达式为 )(2cos 1Tt x A y +π=λ，在x = 0处发生反射，反射点为一固定端．设反射时无能量损失，求：(1) 反射波的表达式 (2) 合成的驻波的表达式．解：(1) 反射点是固定端，所以反射有相位突变π，且反射波振幅为A ，因此反射波的表达式为 ])//(2cos[2π+-π=T t x A y λ(2) 驻波的表达式是 21y y y += )21/2c o s ()21/2c o s (2π-ππ+π=T t x A λ 例8-14 如果入射波的表达式是)//(2cos 1λx T t A y +=π，在x = 0处发生反射后形成驻波，反射点为波腹．设反射后波的强度不变，则反射波的表达式y 2 = ； 在x = 2λ /3处质点合振动的振幅等于 ．)(2cos λxT t A -π A/4例8-15 在固定端x = 0处反射的反射波表达式是)/(2cos 2λνx t A y -π=. 设反射波无能量损失，那么入射波的表达式是y 1 = ；形成的驻波的表达式是y = ．])/(2cos[π++πλνx t A )212cos()21/2cos(2π+ππ+πt x A νλ例8-16 驻波表达式为t x A y ωλcos )/2cos(2π=，则2/λ-=x 处质点的振动方程是 ；该质点的振动速度表达式是 ．t A y ωcos 21-= t A ωωsin 2=v例8-17 在驻波中，两个相邻波节间各质点的振动 (A) 振幅相同，相位相同． (B) 振幅不同，相位相同．(C) 振幅相同，相位不同． (D) 振幅不同，相位不同． [ B ]【练习题】8-1 一横波沿绳子传播，其波的表达式为： )2100c o s(05.0x t y π-π= (SI) (1) 求此波的振幅、波速、频率和波长．(2) 求绳子上各质点的最大振动速度和最大振动加速度． (3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差．解：(1) 已知波的表达式为)2100cos(05.0x t y π-π= 与标准形式)/22cos(λνx t A y π-π= 比较得A = 0.05 m ， ν = 50 Hz ， λ = 1.0 m u = λν = 50 m/s(2) 7.152)/(max max =π=∂∂=A t y νv m /s 322max 22max 1093.44)/(⨯=π=∂∂=A t y a ν m/s 2 (3) π=-π=∆λφ/)(212x x ，二振动反相8-2 一平面简谐波，其振幅为A ，频率为ν ．波沿x 轴正方向传播．设t = t 0时刻波形如图所示．则x = 0处质点的振动方程为 (A) ]21)(2cos[0π++π=t t A y ν． (B) ]21)(2cos[0π+-π=t t A y ν．(C) ]21)(2cos[0π--π=t t A y ν． (D)])(2cos[0π+-π=t t A y ν． [ B ]8-3 已知一平面简谐波的表达式为 )cos(dx bt A y -=，（b 、d 为正值常量），则此波的频率ν = ；波长λ = ． b / 2π 2π / dx8-4 一平面简谐机械波沿x 轴正方向传播，波动表达式为)2/cos(2.0x t y ππ-= (SI)，则波速u = ；x = -3 m 处媒质质点的振动加速度a 的表达式为 ．2 m/s )23cos(2.02x t a π+ππ-= (SI) 8-5 一平面简谐波沿x 轴正向传播，其振幅和角频率分别为A 和ω ，波速为u ，设t = 0时的波形曲线如图所示．(1) 写出此波的表达式．(2) 求距O 点为λ/8处质点的振动方程．(3) 求距O 点为λ/8处质点在t = 0时的振动速度． 解：(1) 以O 点为坐标原点．由图可知，该点振动初始条件为0cos 0==φA y ， 0s i n 0<-=φωA v 所以 2/π=φ 波的表达式为]2/)/(c o s [π+-=u x t A y ωω(2) 8/λ=x 处振动方程为]2/)8/2(cos[ππ+-=λλωt A y )4/cos(π+=t A ω (3) )2//2sin(/d d ππ+--=λωωx t A t yt = 0，8/λ=x 处质点振动速度 ]2/)8/2sin[(/d d ππ+--=λλωA t y 2/2ωA -= 8-6 如图所示，有一平面简谐波沿x 轴负方向传播，坐标原点O 的振动规律为)cos(0φω+=t A y ），则B 点的振动方程为 (A) ])/(cos[0φω+-=u x t A y ． (B) )]/([cos u x t A y +=ω．(C) })]/([cos{0φω+-=u x t A y ． (D) })]/([cos{0φω++=u x t A y ． [ D ] 8-7 已知一平面简谐波的表达式为 )24(cos x t A y +π= (SI)． (1) 求该波的波长λ ，频率ν 和波速u的值； (2) 写出t = 4.2 s 时刻各波峰位置的坐标表达式，并求出此时离坐标原点最近的那个波峰的位置． 解：(1) 由波数 k = 2π / λ 得波长 λ = 2π / k = 1 m由 ω = 2πν 得频率 ν = ω / 2π = 2 Hz 波速 u = νλ = 2 m/s(2) 波峰的位置，即y = A 的位置．由 1)24(c o s=+πx t 有 π=+πk x t 2)24( ( k = 0，±1，±2，…) 解上式，有 t k x 2-=． 当 t = 4.2 s 时， )4.8(-=k x m ． 所谓离坐标原点最近，即| x |最小的波峰．在上式中取k = 8， 可得 x = -0.4 的波峰离坐标原点最近．8-8 与例8-3相同8-9 一平面简谐波沿Ox 轴正方向传播，波长为λ．若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ，则P 2点处质点的振动方程为 ；与P 1点处质点振动状态相同的那些点的位置是 ．])(2cos[212φλν++-π=L L t A y λk L x +-=1 ( k = ± 1, ± 2, …)xuOyxOP 1 P 2 L 1 L 28-10 一平面简谐波在弹性媒质中传播，媒质质元从平衡位置运动到最大位移处的过程中： (A) 它的动能转换成势能． (B) 它的势能转换成动能．(C) 它从相邻的一段质元获得能量其能量逐渐增大．(D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小． [ D ] 8-11 一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是 (A) 动能为零，势能最大． (B) 动能为零，势能为零．(C) 动能最大，势能最大． (D) 动能最大，势能为零． [ C ] 8-12 一平面简谐波沿Ox 轴正方向传播，波的表达式为 )/(2cos λνx t A y -π=, 而另一平面简谐波沿Ox 轴负方向传播，波的表达式为 )/(2cos 2λνx t A y +π=， 求：(1) x = λ/4 处介质质点的合振动方程； (2) x = λ/4 处介质质点的速度表达式．解：(1) x = λ /4处 )2/2cos(1ππ-=t A y ν , )2/2cos(22ππ+=t A y ν∵ y 1，y 2反相 ∴合振动振幅A A A A s =-=2, 合振动的初相φ 和y 2的初相一样为π21． 合振动方程 )2/2c o s(ππ+=t A y ν (2) x = λ /4处质点的速度 )2/ 2sin(2/d d v πππ+-==t A t y νν)2cos(2π+ππ=t A νν8-13 在绳子上传播的平面简谐入射波表达式为)2cos(1λωxt A y π+=，入射波在x = 0处绳端反射，反射端为自由端．设反射波不衰减，证明形成的驻波表达式为：t xA y ωλcos )2cos(2π=证明：入射波在x = 0处引起的振动方程为 t A y ωcos 10=，由于反射端为自由端，所以反射波在O 点的振动方程为 t A y ωcos 20=∴ 反射波为 )2c o s (2λωxt A y π-=驻波方程21y y y +=)2cos(λωx t A π+=)2cos(λωx t A π-+t x A ωλcos )2cos(2π= 8-14 如图所示，两相干波源在x 轴上的位置为S 1和S 2，其间距离为d = 30 m ，S 1位于坐标原点O ．设波只沿x 轴正负方向传播，单独传播时强度保持不变．x 1 = 9 m 和x 2 = 12 m 处的两点是相邻的两个因干涉而静止的点．求两波的波长和两波源间最小相位差．解：设S 1和S 2的振动相位分别为φ 1和φ 2．在x 1点两波引起的振动相位差 ]2[]2[1112λφλφx x d π---π-π+=)12(K 即 π+=-π--)12(22)(112K x d λφφ ① 在x 2点两波引起的振动相位差 ]2[]2[2122λφλφxx d π---π-π+=)32(K即 π+=-π--)32(22)(212K x d λφφ ②②－①得 π=-π2/)(412λx x 6)(212=-=x x λ m由① π+=-π+π+=-)52(22)12(112K x d K λφφ当K = -2、-3时相位差最小π±=-12φφ。
平面简谐波波动方程高中物理 选择性必修第一册如果所传播的是谐振动，且波所到之处，媒质中各质点均做同频率、同振幅的谐振动，这样的波称为简谐波，也叫正弦波或余弦波。
如果简谐波的波面是平面，这样的简谐波称为平面简谐波。
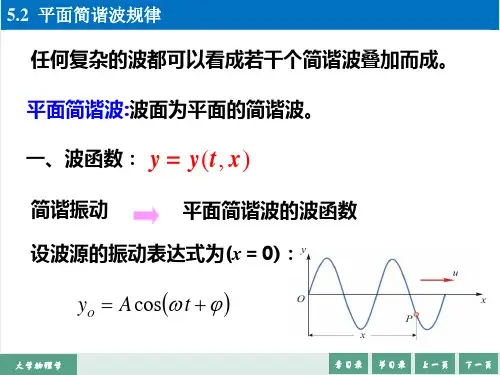
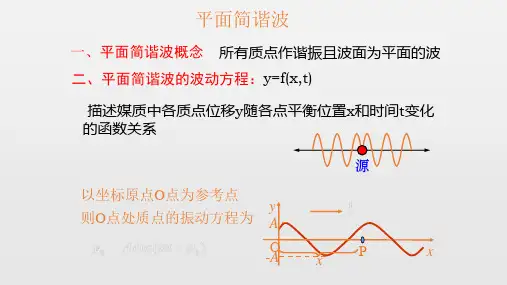
一、平面简谐波·································设波的波长为 ，t 时刻波源的相位为 ,而从波源开始、沿着波的传播方向，每经过一个波长 的质点，其振动状态就与波源的振动状态相同，但振动依次滞后一个周期 T ,即振动相位依次滞后一个2π，则沿波的传播方向、距波源 x 处的质点，振动相位相对波源就滞后 ，故该时刻波的图像的方程为：二、波的图像的方程0ϕ2xπλ⋅λλ0sin(2)xy A πϕλ=-⋅+o m /y m /x v λ例1.写出如图所示波的图像的方程.sin(2)xy A πλ=⋅A A -解：O A A -v λm /y /mx cos(2)xy A πλ=⋅例2.写出如图所示波的图像的方程.解：沿传播方向O x 上的任一点P ，它离O 点的距离为x ，当波源O 振动传到P 点时，P 点处的质点将重复O 点处的质点的振动，角频率也相同，但是振动的相位要落后O 点。
因为0的振动传到P 点需要时间 ，所以P 处质点在时刻t 的振动相位和O 处质点在时刻 的振动相位一样，即有P 处质点在时刻t 的位移为：x v'x t t v =-0sin (x y A t v ωϕ⎡⎤=-+⎢⎥⎣⎦22f Tπωπ== 角频率，也称圆频率，表示单位时间内变化的相角弧度值。
平面简谐波的波函数表达式
平面简谐波是一种特殊的波形，它的波函数表达式可以用以下公式表示：
y = A sin(ωt + φ)
其中，y表示波的振幅，A表示最大振幅，ω表示角频率，t表示时间，φ表示初相位。
平面简谐波是一种具有周期性的波形，它的周期T可以用以下公式计算：
T = 2π/ω
角频率ω是一个常数，它表示单位时间内波形的变化次数。
因此，角
频率越大，波形变化的速度就越快，周期就越短。
初相位φ是一个常数，它表示波形在t=0时的相位。
不同的初相位会导致波形的相位差异，从而产生不同的波形。
平面简谐波的波函数表达式可以用于描述许多物理现象，例如声波、
电磁波等。
在声学中，平面简谐波可以用于描述声音的振动，而在电磁学中，平面简谐波可以用于描述电磁场的振动。
平面简谐波的振幅和角频率是两个重要的参数，它们可以影响波形的形状和特性。
振幅越大，波形的振动幅度就越大，而角频率越大，波形的变化速度就越快。
平面简谐波还具有一些重要的性质，例如叠加原理和相位差。
叠加原理指出，当两个或多个平面简谐波叠加在一起时，它们的振幅可以相加，从而形成一个新的波形。
相位差指出，当两个平面简谐波的相位差为0时，它们的振幅可以相加，而当相位差为π时，它们的振幅可以相消。
总之，平面简谐波是一种重要的波形，它的波函数表达式可以用于描述许多物理现象。
了解平面简谐波的特性和性质，可以帮助我们更好地理解和应用它们。
