高数闭区间上连续函数的性质教案
- 格式:doc
- 大小:31.50 KB
- 文档页数:2


第17、18课时:【教学目的】1、 掌握闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质;2、 熟练掌握零点定理及其应用。
【教学重点】1、介值性定理及其应用;2、零点定理及其应用。
【教学难点】介值性定理及其应用§1. 10 闭区间上连续函数的性质一、有界性与最大值与最小值最大值与最小值: 对于在区间I 上有定义的函数f (x ), 如果有x 0∈I , 使得对于任一x ∈I 都有f (x )≤f (x 0 ) (f (x )≥f (x 0 )),则称f (x 0 )是函数f (x )在区间I 上的最大值(最小值).例如, 函数f (x )=1+sin x 在区间[0, 2π]上有最大值2和最小值0. 又如, 函数f (x )=sgn x 在区间(-∞, +∞)内有最大值 1和最小值-1. 在开区间(0, +∞)内, sgn x 的最大值和最小值都是1. 但函数f (x )=x 在开区间(a , b )内既无最大值又无最小值.定理1(最大值和最小值定理)在闭区间上连续的函数在该区间上一定能取得它的最大值和最小值.定理1说明, 如果函数f (x )在闭区间[a , b ]上连续, 那么至少有一点ξ1∈[a , b ], 使f (ξ1)是f (x )在[a , b ]上的最大值, 又至少有一点ξ 2∈[a , b ], 使f (ξ 2)是f (x )在[a , b ]上的最小值.注意: 如果函数在开区间内连续, 或函数在闭区间上有间断点, 那么函数在该区间上就不一定有最大值或最小值.例: 在开区间(a , b ) 考察函数y =x .又如, 如图所示的函数在闭区间[0, 2]上无最大值和最小值.⎪⎩⎪⎨⎧≤<+-=<≤+-==21 31 110 1)(x x x x x x f y .定理2(有界性定理)在闭区间上连续的函数一定在该区间上有界.二、零点定理与介值定理零点: 如果x 0 使f (x 0 )=0, 则x 0 称为函数f (x )的零点.定理3(零点定理)设函数f (x )在闭区间[a , b ]上连续, 且f (a )与f (b )异号, 那么在开区间(a , b )内至少有一点ξ 使f (ξ)=0.定理4(介值定理)设函数f (x )在闭区间[a , b ]上连续, 且在这区间的端点取不同的函数值f (a )=A 及f (b )=B ,那么,对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得f(ξ)=C.定理4'(介值定理)设函数f(x)在闭区间[a,b]上连续,且f(a)≠f(b),那么,对于f(a)与f(b)之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得f(ξ)=C.证:设ϕ(x)=f(x)-C,则ϕ(x)在闭区间[a,b]上连续,且ϕ(a)=A-C与ϕ(b)=B-C异号.根据零点定理,在开区间(a,b)内至少有一点ξ使得ϕ(ξ)=0 (a<ξ<b).但ϕ(ξ)=f(ξ)-C,因此由上式即得f(ξ)=C (a<ξ<b).定理4 的几何意义:连续曲线弧y=f(x)与水平直线y=C至少交于一点.推论在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值.例1.证明方程x 3-4x 2+1=0在区间(0, 1)内至少有一个根.证:函数f(x)= x 3-4x 2+1在闭区间[0, 1]上连续,又f(0)=1>0,f(1)=-2<0.根据零点定理,在(0, 1)内至少有一点ξ,使得f(ξ)=0,即ξ 3-4ξ 2+1=0 (0<ξ<1).这等式说明方程x 3-4x 2+1=0在区间(0, 1)内至少有一个根是ξ.。






高数闭区间上连续函数的性质教案一、教学目标:1. 让学生理解闭区间上连续函数的概念。
2. 让学生掌握闭区间上连续函数的基本性质。
3. 让学生能够运用闭区间上连续函数的性质解决问题。
二、教学内容:1. 闭区间上连续函数的定义。
2. 闭区间上连续函数的基本性质。
3. 闭区间上连续函数的例子。
三、教学重点与难点:1. 教学重点:闭区间上连续函数的定义及其基本性质。
2. 教学难点:闭区间上连续函数的证明及其应用。
四、教学方法:1. 采用讲解法,系统地介绍闭区间上连续函数的概念和性质。
2. 采用案例分析法,通过具体的例子让学生理解闭区间上连续函数的性质。
3. 采用问题驱动法,引导学生运用闭区间上连续函数的性质解决问题。
五、教学安排:1. 第一课时:介绍闭区间上连续函数的定义。
2. 第二课时:介绍闭区间上连续函数的基本性质。
3. 第三课时:介绍闭区间上连续函数的例子。
4. 第四课时:讲解闭区间上连续函数的证明方法。
5. 第五课时:运用闭区间上连续函数的性质解决问题。
六、教学内容:1. 闭区间上连续函数的介值定理(Bolzano定理)。
2. 闭区间上连续函数的极值存在定理。
七、教学重点与难点:1. 教学重点:介值定理和极值存在定理的证明及其应用。
2. 教学难点:介值定理和极值存在定理的证明过程中的逻辑推理。
八、教学方法:1. 采用证明法,详细讲解介值定理和极值存在定理的证明过程。
2. 采用实例分析法,通过具体的例子让学生理解介值定理和极值存在定理的应用。
3. 采用互动讨论法,引导学生探讨闭区间上连续函数的性质及其与其他数学概念的联系。
九、教学安排:1. 第六课时:介绍闭区间上连续函数的介值定理,讲解定理的证明及应用。
2. 第七课时:介绍闭区间上连续函数的极值存在定理,讲解定理的证明及应用。
3. 第八课时:通过实例分析,让学生更好地理解介值定理和极值存在定理的实际应用。
4. 第九课时:开展小组讨论,探讨闭区间上连续函数的性质及其与其他数学概念的联系。

高数闭区间上连续函数的性质教案教案章节一:引言与预备知识1. 教学目标:使学生了解闭区间上连续函数的概念,掌握一些基本的预备知识,如集合、函数、极限等。
2. 教学内容:(1) 集合的基本概念,如集合的表示方法、集合的运算等。
(2) 函数的基本概念,如函数的定义、函数的表示方法、函数的性质等。
(3) 极限的基本概念,如极限的定义、极限的性质、极限的计算等。
3. 教学方法:采用讲解、例题、讨论等方式进行教学。
4. 教学评估:通过课堂提问、作业、小测验等方式评估学生的学习情况。
教案章节二:闭区间上连续函数的定义1. 教学目标:使学生了解闭区间上连续函数的定义,并能运用该定义判断函数的连续性。
2. 教学内容:(1) 闭区间上连续函数的定义。
(2) 连续函数的性质,如单调性、周期性等。
3. 教学方法:采用讲解、例题、讨论等方式进行教学。
4. 教学评估:通过课堂提问、作业、小测验等方式评估学生的学习情况。
教案章节三:闭区间上连续函数的图像1. 教学目标:使学生了解闭区间上连续函数的图像特征,并能运用这些特征分析函数的性质。
2. 教学内容:(1) 连续函数的图像特征,如连续函数的单调区间、极值点等。
(2) 连续函数的图像绘制方法,如解析法、数值法等。
3. 教学方法:采用讲解、例题、讨论等方式进行教学。
4. 教学评估:通过课堂提问、作业、小测验等方式评估学生的学习情况。
教案章节四:闭区间上连续函数的极限1. 教学目标:使学生了解闭区间上连续函数的极限概念,并能运用极限的性质计算极限。
2. 教学内容:(1) 闭区间上连续函数的极限定义。
(2) 极限的性质,如极限的存在性、唯一性、保号性等。
(3) 极限的计算方法,如直接计算法、夹逼定理法、单调有界定理法等。
3. 教学方法:采用讲解、例题、讨论等方式进行教学。
4. 教学评估:通过课堂提问、作业、小测验等方式评估学生的学习情况。
教案章节五:闭区间上连续函数的连续性1. 教学目标:使学生了解闭区间上连续函数的连续性概念,并能运用连续性的性质判断函数的连续性。

第四章函数的连续性§2连续函数的性质§2 连续函数的性质一、连续函数的局部性质二、区间上连续函数的性质三、反函数的连续性四、一致连续性),)()(()()(00x f x f x f x f ≥≤[,],.a b 上的整体性质证明将在第七章里给出在本节中将研究 f 在二、闭区间上连续函数的性质 定义1 ().f x D 设为定义在数集上的一个函数若 ()(),f x D 则称在上有最大小值0()x 称为最大小值0()()().f x f x D 称为在上的最大小值点,0,x D x D ∈∈存在使得对于任意有.],[上连续在闭区间设b a f的最大值不存在,最小值为零.注意: 定理4.6(最大、最小值定理) ()f x 若函数在闭区()[,].f x a b 则在上有最大、最小值x y sgn =例如,符号函数 的最大值为1,最小值为-1;x y sin =正弦函数的最大值为1,最小值为-1;函数 这个定理刻画了闭区间上连续函数的一个深刻的内涵,在今后的学习中 有很广泛的应用.既无最大值,又无最小值.22y x =-ππsin (,)在上][x x y -=[,]a b 间上连续,推论 )(,],[)(x f b a x f 则上连续在闭区间若函数.],[上有界在b a (0,1).在上无界(),函数有最大、最小值从而有上界与f x 这是因为由定理4.6 可知, 下界,于是 f (x ) 在[a , b ] 上是有界的.1(),(0,1)f x x x =∈函数虽然也是连续函数,但是 这说明定义在开区间和闭区间上的连续函数的性 质有着根本的区别.定理4.7(介值性定理)],[)(b a x f 在闭区间设函数(()()()()),f a f b f b f a μμ<<<<间的任一数或.)(0μ=x f .)()(b f a f ≠且()()f a f b μ若是介于与之上连续, 使得,),(0b a x ∈则(至少)存在一点从几何上看,当连续曲线从水平直线 ()y f x =y μ=的一侧穿到另一侧时, 两者至少有一个交点. ()y f x =∙yxo )(a f )(b f μa b 0x推论(根的存在性定理) ,],[)(上连续在若b a x f 0)(0=x f 应当注意, 此推论与定理4.7是等价的. 于是, 只要 则至少存在一点 ,0)()(<⋅b f a f ,0x 使证明了推论, 也就完成了定理4.7 证明.由介值性定理与最大、最小值定理立刻得到如下 ].,[)],[(M m b a f 下面再举一些应用介值性定理的例题.设在 上连续, 那么它的最大值 M 与最 ],[b a ()f x 结论:小值 m 存在, 并且.nx r =使得证 先证存在性:,lim .n x n x →+∞=+∞因为为正整数所以由极限的保号.1r x n >()n f x x =又因为函数在1,x 性知,存在使 01(0,),x x ∈.0r x n =使得 00n x x r =这个我们记为(读作 r 的 n 次算术根). 例30,r n >若为正整数,则存在唯一的正数 ,0x ,)()0(1x f r f <<且连续, 1[0,]x 上所以由介值定理存在))((1221----++++-=-n n n n n n x yx x y yx y x y ,0>()[0,)nf x x =+∞在上我们只需证明 严格递增 ,,0,x y x y ∀≤<使有即可. 事实上,).()(y f x f <即 000[,],().x a b f x x ∈=存在使例4 .],[]),([],[b a b a f b a f ⊂上连续,在设求证: 再证唯一性:,)()(x x f x F -=.0))(())(()()(<-⋅-=⋅b b f a a f b F a F 则(),().a f a f b b <<现设作辅助函数证 .)(,)(b b f a f a ≤≤由条件知.则结论成立()(),a f a b f b ==若或()[,],f x a b 因在上连续()[,].F x a b 故在上也连续.)(00x x f =),,(0b a x ∈由介值性定理,存在0()0F x =使,即谢谢!。
课题函数的连续性、闭区间上连续函数的性质课时2课时(90 min)教学目标知识技能目标:(1)掌握连续函数的概念。
(2)能够判断函数的间断点,熟悉间断点的分类。
(3)理解初等函数的连续性,能够计算函数的连续区间.(4)理解闭区间上连续函数的性质。
思政育人目标:通过与实际现象联系,帮助学生理解函数的连续性,使学生体会到数学是源于生活的,是对实际问题的抽象产生的,不是脱离实际生活的;引导学生养成独立思考和深度思考的良好习惯;培养学生的逻辑思维、辩证思维和创新思维能力教学重难点教学重点:连续函数的概念、函数在某点连续性的判断教学难点:计算函数的连续区间教学方法讲授法、问答法、讨论法、演示法、实践法教学用具电脑、投影仪、多媒体课件、教材教学设计第1节课:考勤(2 min)→知识讲解(35 min)→问题讨论(10 min)第2节课:知识讲解(20 min)→问题讨论(10 min)→课堂测验(10 min)→课堂小结(5 min)教学过程主要教学内容及步骤设计意图第一节课考勤(2 min)⏹【教师】清点上课人数,记录好考勤⏹【学生】班干部报请假人员及原因培养学生的组织纪律性,掌握学生的出勤情况知识讲解(35 min)⏹【教师】讲解连续函数的概念,并通过例题讲解介绍其应用案例[平面内曲线]在坐标平面内画一连续曲线()y f x=,如图1-27所示.在坐标平面内画一间断曲线()y g x=,如图1-28所示.学习连续函数的概念、函数间断点的分类。
边做边讲,及时巩固练习,实现教学做一体化图1-27 图1-28分析 对比两个图形,我们发现:对于()y f x =,当自变量x 的改变量0x ∆→时,函数相应的改变量0y ∆→,如图1-27所示;对于()y g x =,当自变量x 的改变量0x ∆→时,函数相应的改变量y ∆不能够无限变小,如图1-28所示.于是我们可以用增量来定义函数的连续性.定义1 设函数()y f x =在点0x 的某个邻域内有定义,如果000lim lim[()()]0x x y f x x f x ∆→∆→∆=+∆-=,则称函数()f x 在点0x 处连续.若记0x x x =+∆,则0x x x ∆=-,相应地函数()f x 的增量0()()y f x f x ∆=-.当0x ∆→,即0x x →时,0y ∆→,0()()0f x f x -→,也即0()()f x f x →.因此,函数()y f x =在点0x x =处连续的定义也可表述如下: 定义1' 设函数()y f x =在0x 点的某一个邻域内有定义,若0lim ()()x x f x f x →=,则称函数()f x 在0x 点连续.由函数()y f x =在0x 点连续的定义可知,函数()f x 在0x 点连续,必须同时满足下面三个条件: (1)()f x 在0x 点有定义; (2)极限值0lim ()x x f x →存在;(3)极限值0lim ()x x f x →恰好等于()f x 在该点的函数值,即目 录0lim ()()x x f x f x →=.若00()lim ()x x f x f x ++→=存在且等于0()f x ,则称函数()y f x =在0x 点右连续;若00()lim ()x x f x f x --→=存在且等于0()f x ,则称函数()y f x =在0x 点左连续.定理 1 函数()y f x =在0x 点连续⇔函数()y f x =在0x 点左右连续.例1 证明函数2()1f x x =+在1x =处连续.证明一 2()1f x x =+的定义域为R ,所以()f x 在1x =的某邻域有定义.当自变量在1x =处有改变量x ∆时,222(1)1(11)2()y x x x ∆=+∆+-+=∆+∆,因此,20lim lim[2()]0x x y x x ∆→∆→∆=∆+∆=,所以()f x 在1x =处连续.证明二 2()1f x x =+的定义域为R ,所以()f x 在1x =的某邻域有定义,211lim ()lim(1)2x x f x x →→=+=,即1x →时()f x 的极限值为2.而21(1)112lim ()x f f x →=+==,即极限值等于函数在该点的函数值,所以()f x 在1x =处连续.例 2 讨论函数320()20x x f x x x ⎧+=⎨-+<⎩,,,在点0x =的连续性.解 因为30(0)lim ()lim(2)2(0)x x f f x x f +++→→==+==,(0)lim ()lim(2)2(0)x x f f x x f ---→→==-+==, 所以()f x 在0x =点左右连续,故()f x 在点0x =处连续. 函数在一点连续的定义,可以推广到区间上.定义2 如果一个函数在某区间()a b ,内的每一点处都连续,则称这个函数在区间()a b ,内连续,或称其为区间()a b ,内的连续函数.如果函数()y f x =在()a b ,内连续,且a 点右连续,b 点左连续,则称函数()f x 在闭区间[]a b ,上连续. 连续函数的图形是一条连续而不间断的曲线.⏹ 【学生】掌握连续函数的概念⏹ 【教师】讲解函数间断点的分类,并通过例题讲解介绍其应用如果()y f x =在点0x 处不连续,则称点0x x =是函数()f x 的间断点.由()y f x =在0x x =处连续的定义知,如果()f x 在0x 处有以下三种情况之一,则()f x 在0x 处间断: (1)()y f x =在点0x 处无定义; (2)0x x →时0lim ()x x f x →不存在;(3)函数值0()f x 和极限值0lim ()x x f x →都存在,但0lim ()()x x f x f x →≠.例如,函数1()1f x x =+在点1x =-处没有定义,1x =-就是函数1()1f x x =+的一个间断点.如果不考虑函数()f x 在0x 是否有定义,那我们可以将函数的间断点分为以下两大类. 设函数()y f x =在点0x 处间断,但在点0x 的左右极限0()f x -与0()f x +均存在,则称0x 为()f x 的第一类间断点,其中:目 录(1)若00()()f x f x +-=,即极限0lim ()x x f x →存在,则称点0x 是()f x 的可去间断点.(2)若00()()f x f x +-≠,即极限0lim ()x x f x →不存在,则称点0x 是()f x 的跳跃间断点.设函数()y f x =在点0x 处间断,若在点0x 的左右极限0()f x -与0()f x +至少有一个不存在,则称0x 为()f x 的第二类间断点,其中:(1)若0()f x -与0()f x +至少有一个为无穷大,则称点0x 是()f x 的无穷间断点.(2)若0lim ()x x f x →振荡性地不存在,则称点0x 是()f x 的振荡间断点.例3 函数10()0010x x f x x x x +>⎧⎪==⎨⎪-+<⎩,,,,,在点0x =处有定义,且(0)0f =.但由于(0)lim(1)1x f x ++→=+=,(0)lim(1)1x f x --→=-+=,(0)(0)1(0)0f f f +-==≠=,故0x =是函数()f x 的可去间断点,如图1-29所示.但如果将函数()f x 在0x =的定义改为(0)1f =,则函数在0x =点连续.由此可见,如果函数()f x 在0x 点是可去间断点,可通过补充或改变()f x 在0x 点的函数值,使()f x 在0x 点连续.例4 符号函数10()sgn 0010x f x x x x >⎧⎪===⎨⎪-<⎩,,,,,在点0x =处有定义,且(0)0f =.但由于0(0)lim11x f ++→==,0(0)lim(1)1x f --→=-=-,即(0)f +和(0)f -都存在但不相等,故0x =是函数()f x 的跳跃间断点,如图1-30所示.图1-29 图1-30例 5 函数1y x=在点0x =处无定义,由于(0)f +=+∞,(0)f -=-∞,故0x =是函数1y x=的无穷间断点,如图1-31所示.例6 函数1siny x =在点0x =处无定义,取122n x n =ππ-,122nx n '=ππ+(12)n =,,,当n →∞时,0n x →,0n x '→,但()sin 212n f x n π⎛⎫=π-=- ⎪⎝⎭,()sin 212n f x n π⎛⎫'=π+= ⎪⎝⎭,即当0x →时,函数1sinx值在1-与1+之间变动无限多次.故0x =是函数1sinx的振荡间断点,如图1-32所示.图1-31 图1-32例7 判断下列函数在指定点处的连续性,若间断,判别间断目 录点的类型:(1)sin 0()e 10x xx f x x x ⎧<⎪=⎨⎪+⎩,,,在点0x =处;(2)221()32x f x x x -=-+在点11x =和22x =处.解 (1)函数()f x 在点0x =处有定义,且(0)2f =.但sin (0)lim 1x xf x--→==,(0)lim(e 1)2xx f ++→=+=,(0)(0)f f +-≠,故0x =为函数()f x 的跳跃间断点,属于第一类间断点.(2)221(1)(1)()32(1)(2)x x x f x x x x x --+==-+--在11x =,22x =处无定义,故11x =,22x =是()f x 的间断点. 由于111lim ()lim22x x x f x x →→+==--,故11x =是()f x 的可去间断点,属于第一类间断点. 由于221lim ()lim2x x x f x x →→+==∞-,故22x =是()f x 的无穷间断点,属于第二类间断点.⏹ 【学生】掌握函数间断点的分类问题讨论 (10 min )⏹ 【教师】组织学生讨论以下问题1.函数()f x 在点0x 处有定义、有极限、连续三个结论有什么区别与联系.2.若函数()f x 在点0x 处无定义,则0x 点是函数()f x 的第一类间断点,还是第二类间断点?通过课堂讨论,活跃课堂气氛,加深学生对知识点的理解3.分段函数()()()g x x af xh x x a⎧=⎨<⎩,,,在分段点x a=一定是间断点吗?⏹【学生】讨论、发言第二节课知识讲解(20 min)⏹【教师】讲解初等函数的连续性,并通过例题讲解介绍其应用1.连续函数的和、差、积、商的连续性根据函数在某点连续的定义和极限的四则运算法则,可得下面的定理.定理2设函数()f x和()g x在点x连续,则它们的和、差、积、商都在点x连续.例如,由于sin x,cos x在()-∞+∞,上的每一点都连续,故sintancosxxx=和coscotsinxxx=在其各自定义域上每一点都是连续的.2.初等函数的连续性利用函数连续的定义和性质可以证明:六种基本初等函数在其定义域上都是连续的.由于初等函数是由基本初等函数经过有限次四则运算和复合而得到的函数,函数的连续性对四则运算和复合运算是封闭的,所以我们又有结论:所有初等函数在其定义区间上都是连续的.根据这一结论,求初等函数在其定义域内某点的极限时,只要求出该点的函数值即可.例8求4e cos(4)lim3xxxx→+--.解由于该函数是初等函数,且在4x=处有定义,故由初等函数的连续性可以得出学习初等函数的连续性、闭区间上连续函数的性质。
第17、18课时:
【教学目的】
1、 掌握闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质;
2、 熟练掌握零点定理及其应用。
【教学重点】
1、介值性定理及其应用;
2、零点定理及其应用。
【教学难点】
介值性定理及其应用
§1. 10 闭区间上连续函数的性质
一、有界性与最大值与最小值
最大值与最小值: 对于在区间I 上有定义的函数f (x ), 如果有x 0∈I , 使得对于任一x ∈I 都有
f (x )≤f (x 0 ) (f (x )≥f (x 0 )),
则称f (x 0 )是函数f (x )在区间I 上的最大值(最小值).
例如, 函数f (x )=1+sin x 在区间[0, 2π]上有最大值2和最小值0. 又如, 函数f (x )=sgn x 在区间(-∞, +∞)内有最大值 1和最小值-1. 在开区间(0, +∞)内, sgn x 的最大值和最小值都是1. 但函数f (x )=x 在开区间(a , b )内既无最大值又无最小值.
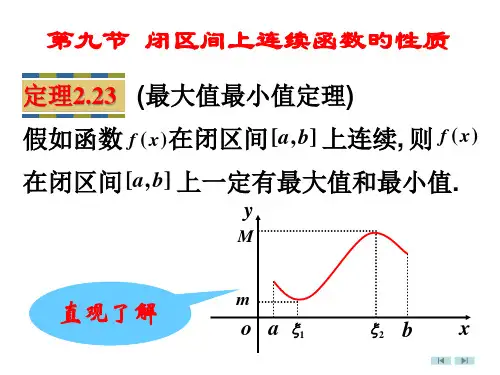
定理1(最大值和最小值定理)在闭区间上连续的函数在该区间上一定能取得它的最大值和最小值.
定理1说明, 如果函数f (x )在闭区间[a , b ]上连续, 那么至少有一点ξ1∈[a , b ], 使f (ξ1)是f (x )在[a , b ]上的最大值, 又至少有一点ξ 2∈[a , b ], 使f (ξ 2)是f (x )在[a , b ]上的最小值.
注意: 如果函数在开区间内连续, 或函数在闭区间上有间断点, 那么函数在该区间上就不一定有最大值或最小值.
例: 在开区间(a , b ) 考察函数y =x .
又如, 如图所示的函数在闭区间[0, 2]上无最大值和最小值.
⎪⎩⎪⎨⎧≤<+-=<≤+-==2
1 31 110 1)(x x x x x x f y .
定理2(有界性定理)在闭区间上连续的函数一定在该区间上有界.
二、零点定理与介值定理
零点: 如果x 0 使f (x 0 )=0, 则x 0 称为函数f (x )的零点.
定理3(零点定理)设函数f (x )在闭区间[a , b ]上连续, 且f (a )与f (b )异号, 那么在开区间(a , b )内至少有一点ξ 使f (ξ)=0.
定理4(介值定理)设函数f (x )在闭区间[a , b ]上连续, 且在这区间的端点取不同的函数值
f (a )=A 及f (b )=B ,
那么,对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得
f(ξ)=C.
定理4'(介值定理)设函数f(x)在闭区间[a,b]上连续,且f(a)≠f(b),那么,对于f(a)与f(b)之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得
f(ξ)=C.
证:设ϕ(x)=f(x)-C,则ϕ(x)在闭区间[a,b]上连续,且ϕ(a)=A-C与ϕ(b)=B-C异号.根据零点定理,在开区间(a,b)内至少有一点ξ使得
ϕ(ξ)=0 (a<ξ<b).
但ϕ(ξ)=f(ξ)-C,因此由上式即得
f(ξ)=C (a<ξ<b).
定理4 的几何意义:连续曲线弧y=f(x)与水平直线y=C至少交于一点.
推论在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值.
例1.证明方程x 3-4x 2+1=0在区间(0, 1)内至少有一个根.
证:函数f(x)= x 3-4x 2+1在闭区间[0, 1]上连续,又f(0)=1>0,f(1)=-2<0.
根据零点定理,在(0, 1)内至少有一点ξ,使得f(ξ)=0,即ξ 3-4ξ 2+1=0 (0<ξ<1).
这等式说明方程x 3-4x 2+1=0在区间(0, 1)内至少有一个根是ξ.。