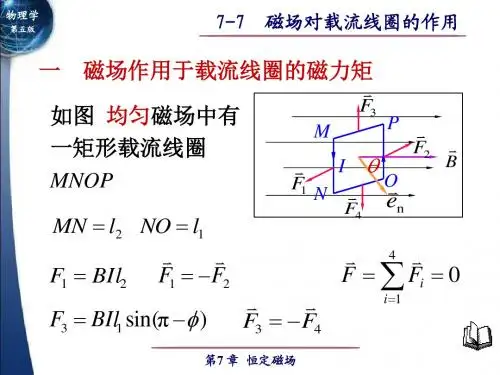
磁场对载流矩形线圈的作用
- 格式:pdf
- 大小:97.40 KB
- 文档页数:3

磁场对载流矩形线圈的作用首先,当通过矩形线圈的电流存在于磁场中时,磁场可以对线圈施加力。
根据安培力定律,当电流通过一条导线时,会产生一个磁场,而这个磁场会与外部磁场相互作用。
根据洛伦兹力定律,线圈中的载流电流会受到磁力的作用。
这个磁力的大小和方向可以通过右手定则来确定。
具体来说,当顺时针电流经过矩形线圈时,它将会受到一个由磁场指向线圈中心的力。
当逆时针电流经过矩形线圈时,它将会受到一个由线圈中心指向磁场的力。
这个磁力对线圈的作用是非常重要的,因为它可以使线圈产生转动力矩,从而实现对物体的控制。
例如,磁场对于电动机和发电机的转子控制起着至关重要的作用。
其次,磁场可以改变载流矩形线圈中的电流。
根据法拉第电磁感应定律,当一个导体(如线圈)在磁场中运动时,它会感应出一种电动势,从而产生电流。
这个电动势的大小和方向可以通过法拉第右手规则来确定。
具体来说,当矩形线圈在磁场中运动时,其每一条边在磁场中感应出的电动势都是不同的。
根据线圈的形状和磁场的作用方向,电动势的大小和方向也会有所不同。
因此,线圈中的电流会随着线圈在磁场中的位置和运动方式而改变。
这个现象被广泛应用于许多电子设备中,比如发电机和变压器。
综上所述,磁场对载流矩形线圈的作用是多方面的。
它可以对线圈施加力,并且可以改变线圈中的电流。
这些作用在许多电子设备中起着至关重要的作用,帮助实现对物体的控制和电能的转换。
1. Serway, R.A., Beichner, R.J., & Jewett, J.W. (2000). Physics for Scientists and Engineers (5th ed.). Brooks/Cole Publishing.。




教学要求了解磁场对载流线圈的作用,熟练地应用安培环路定理解决问题。
10.2.2 安培环路定理的应用与利用高斯定理可以方便地计算出某些具有对称性带电体的电场分布一样,利用安培环路定理也可以方便地计算出具有特殊对称性的载流导线所产生的磁场。
下面讨论几个简单的应用。
利用安培环路定理求磁场分布一般思路:首先依据电流的对称性分析磁场分布的对称性,然后再根据定理计算磁感应强度的数值和方向。
此过程中决定性的技巧是选取合适的闭合路径L (也称安培环路),以便使积分d LB l ⋅⎰中的B 能从积分号内提出来。
1 “无限长”载流圆柱形导线内外磁场分布设“无限长”载流圆柱形导线的圆柱体半径为R ,通有电流I ,电流均匀地分布在圆柱体横截面。
如图10-23(a)所示。
显然,场源电流对中心轴线分布对称,因此无限长载流圆柱形导线的磁场分布具有轴对称性,磁感线是一组分布在垂直于轴线的平面上并以轴线为中心的同心圆,磁感应强度B 的大小只与场点P 到载流圆柱轴线的垂直距离r 有关,故可取垂直于柱轴、且以柱轴上一点O 为圆心、r 为半径的圆周作为闭合路径L [图10-23(a)]。
在所取的同一闭合圆周路径L 上,各点的磁感应强度的大小相等。
B 的方向与电流构成右手螺旋关系:在通过场点P 的导线横截面上[图10-23(b)],取一对面积元1d S 和2d S ,它们关于连线OP 对称。
设1d B 和2d B 是以1d S 和2d S 为横截面的长直电流在点P 的磁感应强度。
从图示的关系可以看出,它们对闭合路径L 在点P 的切线对称,故合矢量12d d d B B B =+沿L 的切线方向(即垂直于半径r )。
由于整个柱截面可以成对地分割成许多对称的面积元,以对称面积元为横截面的每对长直电流在点P 的磁感应强度(合矢量)也都沿L 的切线方向。
因此,通过整个截面的总电流I 在点P 的磁感应强度B ,必沿圆周L 的切线方向。
对所选的闭合圆周L ,由安培环路定理得d 2π'LB l B r I μ⋅=⋅=⎰或 02πI B rμ'=I '表示穿过环路L 的电流。

磁场对载流导体的作用讲授课23 空调01/021、掌握磁场对载流导体的作用重点:磁场对载流导体的作用难点:磁场对载流导体的作用措施:以图示和公式的推导说明《电工基础教学参考书》习题册P27-28§3-4 磁场对载流导体的作用一、磁场对载流直导体的作用:1、大小:通电直导体周围存在磁场(电流的磁效应),它就成了一个磁体,把这个磁体放到另一个磁场中,也会受到磁力的作用,这就是“电磁生力”。
电磁力:指通电导体在磁场中受到的作用力。
电磁力的大小:F=BILsinα式中:F——通电导体受到的电磁力。
牛(N)B——磁感应强度。
特斯拉(T)I——导体中的电流强度。
安培(A)L——导体在磁场的长度。
米(m)α——电流方向与磁感应线的夹角。
当α=90°时,F=BILsinα最大,F=BIL当α=0°时,F=BILsinα最小,等于02、方向通电导体在磁场内的受力方向,可用左手定则判断:平伸左手,使拇指垂直其余四指,手心正对磁场的方向,四指指向表示电流的方向,拇指的指向就是通电导体的受力方向。
3、相距较近且相互平等的通电直导体之间的关系:由于每根载流导线的周围都产生磁场,所以每根导线都处在另一根导线产生的磁场中,即两根导线都受到电磁力的作用。
结论:通过同方向电流的平行导线是互相吸引的,通过反方向电流的平行导线是互相排斥的。
如:输电线上为什么要相距一定距离就安装一个绝缘支柱?4、讲解P59 例3-1二、磁场对通电矩形线圈的作用。
1、线圈平面与磁感应线平行:ab和cd与磁力线垂直将受到磁场的作用力F1和F2,而且F1=F2,根据左手定则,F1和F2的方向相反。
受到作用力的两个边叫做有效边。
两有效边所受到力大小相等,方向相反。
构成一对力偶。
此时的转矩为:M=F1L2=BIL1L2=BIS当线圈平面与磁力线的夹角为α时:M=BIScosα当线圈由N匝线构成时:M=NBIScosα当α=0°时,M=NBIScosα最大,M=NBIS 当α=90°时,线圈平面与磁感应线垂直:M=NBIScosα最小,等于02、讲解P60 例3-2。



均匀磁场中矩形载流线圈的受力分析
一、引言
磁力在物理和工程学中有着极其重要的地位,它可以用来解释和分析
许多物理现象,也可以用来控制和利用物理系统。
磁力的行为受磁场强度
影响,而磁场强度又受磁体结构和周围磁性环境的影响,因此,磁力的正
确分析非常重要。
本文致力于研究均匀磁场中矩形载流线圈的受力情况,以便为矩形载
流线圈的实际应用提供设计参考。
载流线圈的受力分析需要考虑它的物理
结构、磁体的结构参数、外部电路参数以及磁场环境参数。
二、矩形载流线圈的基本几何结构
矩形载流线圈是由四条磁性导线组成的,有两条相交的水平线和两条
竖直线。
这四条导线以外接矩形的形式构成一个闭合的载流线圈,水平线
长度为L1,竖直线长度为L2、载流线圈不能受到外部力的影响,因此,
我们可以假定它是在一个均匀磁场中的最大动力学变形下进行受力分析的。
三、矩形载流线圈在磁场中的受力分析方法
矩形载流线圈在磁场中的受力分析,首先需要计算其介质中存在的电流,其次通过Ampere定律对电流进行分析,推导出磁场在介质中的强度
分布,再根据磁场强度对载流线圈进行受力分析。
载流线圈在磁场中的运动(1) 载流线圈的磁矩
定义载流I的刚性平面线圈S的磁矩为
其中S为线圈的面积,I为刚性平面线圈通过的电流,n为线圈平面的法向,它也是磁矩的方向。
n与电流的方向成右手螺旋关系。
(2) 载流线圈受到的磁力矩
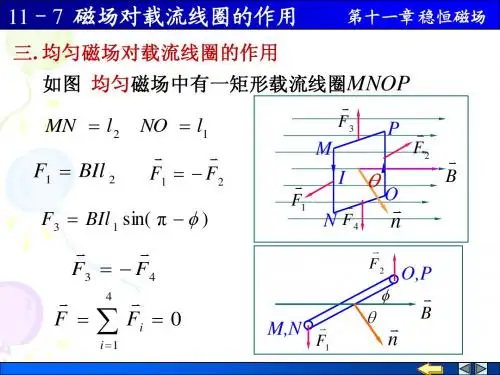
在磁感应强度为B的均匀磁场中,有一刚性矩形平面载流线圈,边长分别为l1和l2,电流为I,如下图所示。
设线圈平面的法向单位矢量n与磁场方向的夹角为j,并且ab边与cd边均与磁场方向垂直。
导线bc和ad所受的安培力F1、F1’大小相等,方向相反,且作用在同一直线上,故相互抵消。
导线ab和cd所受的安培力分别为F2、F2’,并且有F2= F2’=BIl2,但这两个力不在同
一直线,因此形成一力偶(图b)。
所以磁场作用在线圈上的力矩为
根据(14.6.6)式线圈磁矩的定义,上式可写成矢量式
这就是载流线圈在均匀磁场中受到的磁力矩。
当n与B平行时,磁力矩为零;当n与B垂直时,磁力矩不为零;当n与B之间有夹角j时,磁场的平行于线圈法向的分量对线圈无任何影响;磁场的垂直于线圈法向的分量对线圈作用有力矩作用。
如刚性平面载流线圈处于不均匀磁场B中,则用积分求出磁力矩
在非均匀磁场中,载流线圈除受到磁力矩外,还受到磁力的作用。
磁力的方向指向强磁场区域,因此载流小线圈总是被磁极吸引。
河北经济管理学校教案
序号:1 编号:JL/JW/7.5.1.03
11.17授课主题磁场对载流矩形线圈的作用
教学目的1. 电磁转矩的产生
2. 电磁转矩的表达式
3. 霍尔效应
教学重点、难
点重点:
1. 电磁转矩的公式
2. 霍尔效应
教学准备教材、教案、板书、PPT
教学过程设计与时间分配
一、课堂导入与提问(10min)
二、讲授新课(25min)
1.电磁转矩的产生
2.电磁转矩的表达式
3.电动机旋转的基本原理
4.霍尔效应
三、计算举例(30min)
四、课堂小结(15min)
五、布置作业(10min)
河北经济管理学校教案
教案内容
1、 课堂导入与提问(10min)
复习上节课内容,回顾磁场对载流导体的作用,思考:磁场对载流矩形线圈又有什么作用
二、讲授新课(25min)
1.电磁转矩的产生
如课本P92图2-22所示,将一矩形线圈abcd放在匀强磁场中,线圈的上下两边ad和bc所受的磁场力大小相等,方向相反,在一条直线上彼此平衡;而作用在线圈两个侧边ab和cd上的磁场力虽然大小相等,方向相反,但不在一条直线上,产生了力矩,称为电磁转矩
2.电磁转矩的表达式
经推导得出电磁转矩的表达式为:M=NBIScosα
上式中B——均匀磁场的磁感应强度,单位为特(T)
I——线圈中的电流,单位为安(A)
S——线圈的面积,单位为平方米(㎡)
N——线圈的匝数
α——线圈平面与磁力线的夹角,单位为度(°)
M——电磁转矩,单位为牛’米(N’M)
当线圈平面与磁力线平行时,力臂最大,线圈受电磁转矩最大;当线圈平面与磁力线垂直时,力臂为零,线圈受电磁转矩也为零
3.电动机旋转的基本原理
磁场对通电矩形线圈的作用力是电动机旋转的基本原理
4.霍尔效应
金属或半导体薄片置于磁场中,当有电流流过时,在垂直于电流和磁场的方向上将产生电动势,这种物理现象称为霍尔效应
3、 计算举例(30min)
课本P93自我测评第二题
4、 课堂小结(15min)
1.电磁转矩的表达式:M=NBIScosα
2.磁场对通电矩形线圈的作用力是电动机旋转的基本原理
3.霍尔效应:金属或半导体薄片置于磁场中,当有电流流过时,在垂直于电流和磁场的方向上将产生电动势
五、布置作业(10min)
复习本节课所讲内容,了解关于霍尔效应课外知识。