第九节 磁场对载流线圈的作用
- 格式:doc
- 大小:173.50 KB
- 文档页数:4

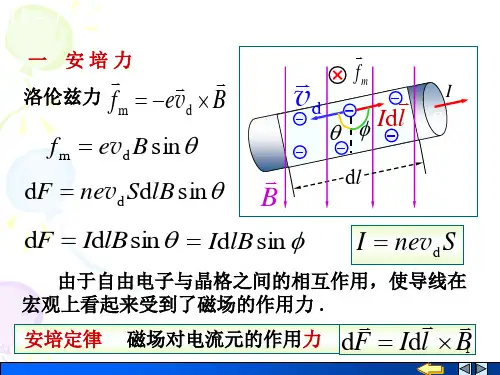




磁场对载流导线的作用一安培力1.安培力:,写成矢量式:。
此式既是一个电流元Idl在外磁场B中受力的基本规律,又是定义磁感应强度B的依据。
二平行无限长直导线间的相互作用如图:设两导线的垂直距离为d,其中电流强度分别为I1,I2,电流方向相同,在导线CD上任取电流元I2dl2,其受力dF2 =B1I2dl2 又由于,且在导线CD中每一电流元受力方向相同,故其每单位长度所受力为:方向:垂直CD指向AB。
同理在导线AB中每单位长度所受力为:方向: 垂直AB指向CD,故两导线相互吸引。
同样可证明当两导线电流方向相反时则两导线相相互斥。
三电流电位的规定在真空中有两根平行的长直导线,它们之间相距1m,两导线上电流的流向相同、大小相等。
当两导线每单位长度上的吸引力为时,导线中流有的电流定义为1A。
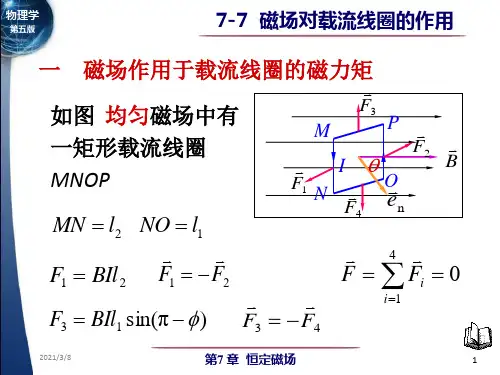
四矩形载流线圈在匀称磁场中所受的力矩在匀称磁场中,有一刚性矩形载流线圈abcd,它的边长分别为l1和l2,电流为I。
设的方向(电流绕行方向的右手螺旋方向)与B方向之间的夹角为。
对于导线ad段和bc段,作用力的大小相等、方向相反,并且在同始终线上,所以它们的合力及合力矩都为零。
而导线ab段和cd段所受磁场作用力的大小则分别为:。
这两个力大小相等、方向相反,但不在同始终线上,因此磁场作用在线圈上的磁力矩的大小为:考虑线圈的磁矩,则上式矢量表示为:假如线圈有N匝,那么其所受的磁力矩应为:考虑下述几种特别状况:(1)当时,线圈平面与B垂直,,此时线圈处于稳定平衡状态;(2)当时,线圈平面与B平行,;(3)当时,线圈平面与B垂直,但载流线圈的方向与B的方向相反,M=0,此时线圈是处于不稳定平衡状态。
不稳定平衡状态稳定平衡状态总之,磁场对载流线圈作用的磁力矩,总是使磁矩M转到磁感强度B 的方向上。

载流导线在磁场中所受的力磁场对载流线圈的作用
物理作业
当一个载流线圈进入到磁场中,磁场会对载流线圈的回路造成影响,引起电流的流动。
1、电流流动
当一个载流线圈进入磁场中,其载体上的电压在机械施加电势差的基础上,受磁场的作用产生另外的电势差,由于存在电势差,就会有电流流动,这就是受磁场作用的结果。
根据霍尔定律,当电流流动时,磁场中的磁感应强度会受到影响,只要有电流流动就会改变磁场中的磁感应强度,进而引起磁场的变化。
2、磁场
当载流线圈进入磁场中时,会产生磁力,这个磁力会对载流线圈的回路造成影响,使其具有电磁能。
电磁能的大小取决于磁力大小,磁力的大小又取决于磁场的强度和磁力矢量的方向,所以,磁场的强度和方向对电磁能的大小起着关键性作用。
3、电磁对抗
当载流线圈进入到磁场中时,磁场会影响载流线圈的回路,使其具有电磁能,电磁能的大小取决于电压和磁力的大小,因此,载流线圈在磁场中的电磁能可以用电压和磁力两个度量表示。
当磁场和电压产生相互作用时,载流线圈会受到电磁对抗的作用,它会发出声音或震动,从而受到磁场的影响。
4、磁通率
当载流线圈进入到磁场中时。
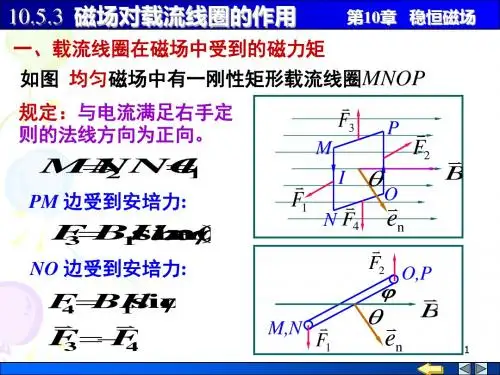
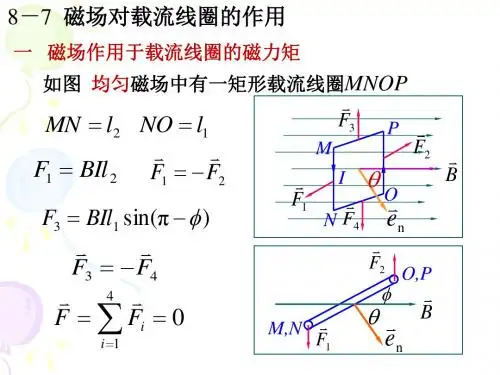
10-7 磁场对载流线圈的作用一、磁场作用于载流线圈的磁力矩下面用安培定律来研究磁场对载流线圈的作用。
如下图所示,在磁感强度为B 的均匀磁场中,有一刚性矩形载流线圈MNOP ,它的边长分别为1l 和2l ,电流为I ,流向自M P O N M →→→→,设线圈平面的单位正法向矢量n e的方向与磁感强度B 方向之间的夹角为θ,即线圈平面与B 之间夹角为φ()2/π=+θφ,并且MN边及OP 边均 与B 垂直。
由安培定律知磁场对导线NO 段和PM 般作用力大小相等,方向相反,并且在同一直线上,所以对整个线圈来讲,它们的合力及合力矩都为零。
导线MN 和OP 段受磁场力大小则分别为21BIl F = 22BIl F =这两个力大小相等,方向亦相反,但不在同一直线上,对线圈要产生磁力矩φcos 11l F M =。
由于θφ-=2/π,所以θφsin cos =,则有θθsin sin 1211l BIl l F M ==或θsin BIS M =(10-17a )式中21l l S =为矩形线圈的面积,磁矩ne m IS =,此处ne 为线圈平面的正法向矢量. 所以上式用矢量表示则为Bm B e M ⨯=⨯=n IS (10-17b )如果线圈不只一匝,而是N 匝,那么线圈所受的磁力矩应为Be M ⨯=n NIS (10-17c )讨论: 载流线圈在均匀磁场中的运动问题(1)当载流线圈的ne 方向与磁感强度B 的方向相同(即︒=0θ),亦即磁通量为正向极大时,M=0,磁力矩为零,此时线圈处于平衡状态[图(a)]。
(2) 当载流线圈的ne 方向与磁感强度B 的方向相垂直(即︒=90θ),亦即磁通量为零时,M=NBIS ,磁力矩最大[图(b)](3)当载流线圈的ne 方向与磁感强度B 的方向相反(即︒=180θ)时,M=0,这时也没有磁力矩作用在线圈上[图(c)],不过,在这种情况下,只要线圈稍稍偏过一个微小角度,它就会在磁力作用下离开这个位置,而稳定在︒=0θ时的平衡状态,总之,磁场对载流线圈作用的磁力矩,总是要使线圈转到它的ne 方向与磁场方向相一致的稳定平衡位置(M10-8)。
10-7 磁场对载流线圈的作用
一、磁场作用于载流线圈的磁力矩
下面用安培定律来研究磁场对载流线圈的作用。
如下图所示,在磁感强度为B 的均匀磁场中,有一刚性矩形载流线圈MNOP ,它的边长分别为1l 和2l ,电流为I ,流向自M P O N M →→→→,设线圈平面的单位正法向矢量n e
的方
向与磁感强度B 方向之间的夹角为θ,即线圈平面与B 之间夹角为φ()
2/π=+θφ,并且MN
边及OP 边均 与B 垂直。
由安培定律知磁场对导线NO 段和PM 般作用力大小相等,方向相反,并且在同一直线上,所以对整个线圈来讲,它们的合力及合力矩都为零。
导线MN 和OP 段受磁场力大小则分别为
21BIl F = 2
2BIl F =
这两个力大小相等,方向亦相反,但不在同一直线上,对线圈要产生磁力矩φ
cos 11l F M =。
由于
θ
φ-=2/π,所以
θ
φsin cos =,则有
θ
θsin sin 1211l BIl l F M ==
或
θsin BIS M =(10-17a )
式中
2
1l l S =为矩形线圈的面积,磁矩
n
e m IS =,此处
n
e 为线圈平面的正法向矢量. 所以上
式用矢量表示则为
B
m B e M ⨯=⨯=n IS (10-17b )
如果线圈不只一匝,而是N 匝,那么线圈所受的磁力矩应为
B
e M ⨯=n NIS (10-17c )
讨论: 载流线圈在均匀磁场中的运动问题
(1)当载流线圈的
n
e 方向与磁感强度B 的方向相同(即︒=0θ),亦即磁通量为正向极大
时,M=0,磁力矩为零,此时线圈处于平衡状态[图(a)]。
(2) 当载流线圈的
n
e 方向与磁感强度B 的方向相垂直(即︒=90θ),亦即磁通量为零时,
M=NBIS ,磁力矩最大[图(b)]
(3)当载流线圈的
n
e 方向与磁感强度B 的方向相反(即︒=180θ)时,M=0,这时也没有磁
力矩作用在线圈上[图(c)],不过,在这种情况下,只要线圈稍稍偏过一个微小角度,它就会在磁力作用下离开这个位置,而稳定在︒=0θ时的平衡状态,总之,磁场对载流线圈作用的磁力矩,
总是要使线圈转到它的
n
e 方
向与磁场方向相一致的稳定
平衡位置(M10-8)。
(4)式(10-17)虽然是从矩形线圈推导出来的,但可以证明它对任意形状的平面线圈都是成立的。
二、例题
如上 图所示,半径为0.20m ,电流为20A ,可绕Oy
轴旋转的圆形载流线圈放在均匀磁场中,
磁感强度B 的大小为0.08T ,方向沿x 轴正向。
问线圈受力情况怎样?线圈受的磁力矩又为多少?
解 把圆线圈分为JKP 和
PQJ
两部分,由安培定律中可知,半圆JKP 所受的力
1
F 为
N
64.0 N 20.02008.022)2(1k k k k F -=⨯⨯⨯-=-=-=BIR R BI
即1
F 的方向与Oz 轴的正向相反,垂直屏幕向里,作用在半圆
PQJ
上的力
2
F 为
N
64.02)2(2k k k F ===BIR R BI
即
2F 的方向与Oz 轴的正向相同,
垂直屏幕向外,因此,作用在圆形载流线圈上的合力为零,
但力矩并不为零。
如上面右图所示,按照力矩的定义,对Oy
轴而言,作用在电流元l I d 上的磁力矩M d 的大小
为
θ
sin d d d lBx I F x M ==
由图可以看出,,d d ,sin θθR l R x ==上式为
于是,作用在整个线圈上的磁力矩M 的大小则为
⎰=π
2 0 22d sin θ
θIBR M
得
2
πR IB M =
力矩M 的方向沿
Oy
轴正向。
上述结果如用式(10-17b )是很容易得到的,读者自己试一试。
三、思考题
1.
如下图,把一载流线圈放入一永久磁铁的磁场中,在磁场的作用下线圈将发
生转动。
(1)图(a )中的线圈怎样转动?
(2)图(b )中的线圈由上往下看是顺时针在转动,问磁铁哪一边是N 极?哪一边是S 极? (3)图(c)中的线圈由上往下看是逆时针在转动,问线圈中电流的流向怎样?
θ
θd sin d 22IBR M =。