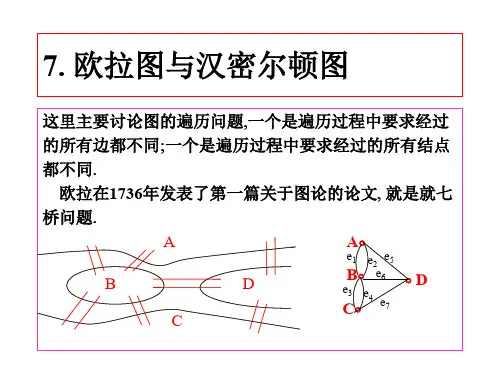
第9章 欧拉图和哈密顿图
- 格式:ppt
- 大小:1011.50 KB
- 文档页数:32









习题91.构造一个欧拉图,其结点树v和边树e满足下述条件1)v、e的奇偶性一样。
2)v、e的奇偶性相反。
如果不可能,说明原因。
解:1)2)2.确定n取怎样的值,无向完全图Kn为欧拉图;n取怎样的值,有向完全图为欧拉图。
解:一个图中若存在欧拉回路,必满足每个结点的度数均为偶数.对于无向完全图K n,deg(v)=n–1。
所以,当n是奇数时,无向完全图K n有一条欧拉回路。
所有有向完全图为欧拉图。
3.确定n取怎样的值,无向完全图Kn为哈密尔顿图;n取怎样的值,有向完全图为哈密尔顿图。
解:n=1或n≥3时,无向完全图K n是哈密尔顿图。
n≥1时,有向完全图为哈密尔顿图.4.1)画一个有一条欧拉回路和一条哈密尔顿回路的图.2)画一个有一条欧拉回路,但没有一条哈密尔顿回路的图。
3)画一个没有一条欧拉回路,但有一条哈密尔顿回路的图。
解:(1)有欧拉回路和哈密尔顿回路;(2)有欧拉回路,但无哈密尔顿回路;(3)无欧拉回路,但有哈密尔顿回路;(4)既无欧拉回路,又无哈密尔顿回路.•••••••••(1)(2)••••••••••(3)(4)5.证明:有桥的图不是哈密尔顿图. 证明:采用反证法。
假设哈密尔顿图G 中存在桥e=(u,v),取结点集V 的一个非空子集S={u},必有W(G-S)≥2。
因为G 为哈密尔顿图,由定理9.1—5,W (G-S )≤|S |=1,与W (G-S)≥2矛盾。
故有桥的图不是哈密尔顿图。
6.证明:有桥的图不是欧拉图. 证明:[方法一]反证法.假设图G 为欧拉图。
利用简单回路的一个性质,设C 为任意的简单回路,e 为C 上任意的边,则c —e 仍连通。
记这个性质为*因为G 为欧拉图,所以存在欧拉回路,设C 为其中的一条欧拉回路,则G 中任何边均在C 上.于是,∀e ∈E (G ),G’=G -e=C —e.由*可知,G’仍连通,故由桥的定义可知,e 不是G 中的桥.由e 的任意性得证,G 中无桥。
8.欧拉图与哈密顿图1.设G为n (n≥2)阶欧拉图,证明G是2-边连通图证明:存在一条欧拉回路,所以去掉其中任何一边e,该图G-e仍然是连通得,去掉两条边,该图可能是不连通的,所以λ(G)≥2,所以该图是2-边连通图2.设G为无向连通图,证明:G为欧拉图当且仅当G的每个块都是欧拉图证明:根据理题G为欧拉图当且仅当G可表示为若干个边不重的圈之并,易证若干个边不重的边,不一定是块。
块是指没有割点的极大连通子图证明:必要性如果G是欧拉图,根据定理8.1及其推论:G是若干边不相交的圈的并,G是欧拉图当且仅当G时连通的且G中无奇度顶点,所以我们在G中找块时,无非就是找割点两侧的圈,割点在每个圈中出现的所得的度数都是偶数,割点为V(V v11,v12,...,v1n,V,v21,v22,...v2nV,v3.....,V)其实很容易证明,割点两侧的圈都是连通的,且度数都为偶数,必要性得证充分性每个块都是欧拉图, 都是圈其中得割点是V1,V2...,Vn,那么V1,v11,v12,...,V2,v21,v22,...,v2n,V3,v31,v32,...v3n,..,V3....,V1得证我觉得思路是正确的,不过证明过程不是很严格(图这部分我还没有认真思考如何写出严格的步骤,以后我会继续研究证明过程!!·!)3.设G恰有2k(k≥1)个奇度顶点的连通图,证明G中存在K条边不重的简单通路P1,P2,…Pk,使得E(G)=U(I=1,k)E(Pi)证明:方法二对k做归纳法(1)k=1时,G为半欧拉图,因而存在欧拉通路P,则P为所求,所以结论为真。
(2)设k=r时,结论为真。
要证:k=r+1时结论为真。
设G的2k=2r+2个奇度顶点分别为V1,V2,…,Vr,Vr+1V1',V2',…,Vr',Vr+1'在Vr+1与Vr+1'之间加一条新边er+1=(Vr+1,Vr+1'),得图G',则G'连通且有2r个奇度顶点。