当前位置：文档之家 › 离散数学--第十五章 欧拉图和哈密顿图

离散数学--第十五章 欧拉图和哈密顿图

  • 格式：ppt
  • 大小：466.50 KB
  • 文档页数：33

下载文档原格式

  / 33

合集下载

离散数学课件15欧拉图与哈密顿图

离散数学课件15欧拉图与哈密顿图
证明 若G是平凡图，结论显然成立。
下面设G为非平凡图，设G是m条边的n阶无 向图，
并设G的顶点集V＝{v1,v2,…,vn}。 必要性。因为G为欧拉图，所以G中存在欧 拉回路，
设C为G中任意一条欧拉回路，vi,vj∈V， v2i0,2v0/7j/都23 在C上，
定理15.1的证明
充分性。由于G为非平凡的连通图可知，G中边数 m≥1。
2020/7/23
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ，且G中恰有两个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0， 对G加新边（u0,v0），得G ＝G∪(u0,v0)， 则G 是连通且无奇度顶点的图， 由定理15.1可知，G 为欧拉图， 因而存在欧拉回路C ，而C＝C -(u0,v0)为G中一 条欧拉通路， 所以G为半欧拉图。
并2行从020/7遍/C23 上G 的i中某的顶欧点拉vr回开路始C行遍i，，i＝每1遇,2,到…v,s*j，i，最就后
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ，且G中恰有两个奇度顶点。
证明 必要性。设G是m条边的n阶无向图，因为G为 半欧拉图， 因而G中存在欧拉通路(但不存在欧拉回路)， 设Г＝vi0ej1vi1…vim-1ejmvim为G中一条欧拉通路， vi0≠vim。 v∈V(G)，若v不在Г的端点出现，显然d(v)为偶 数， 若v在端点出现过，则d(v)为奇数，
欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究！有许多公式、定理、解法、函数、方程、常数等 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法”。欧拉还是数学符号发明者，他创设 的许多数学符号，例如π，i，e，sin，cos，tg，Σ，f (x)等等， 至今202沿0/7/2用3 。

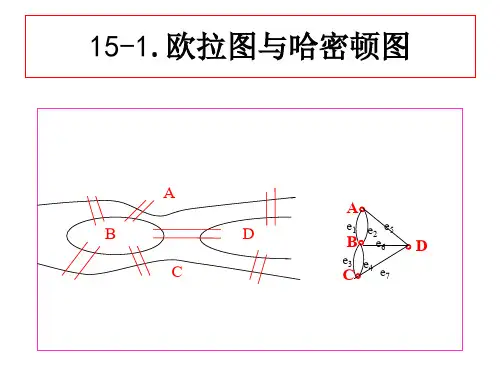
【离散数学讲义】7.Euler图52

【离散数学讲义】7.Euler图52

中国邮递员问题（E-图？） (The Chinese postman problem)
一个邮递员送信, 每次要走遍他负责投递范围内 的街道, 然后再回到邮局. 问他应该按怎样的路线 走, 使所走的路程最短? 如果用点表示交叉路口, 用点之间的连线表示对 应的街道, 每条线上对应一个实数, 它是相应街道 的长度. 原问题变成一个图论问题. 中国邮递员问题: 在赋以非负权的连通图G上, 求 一条最小权环游.(称为最优环游或最佳邮路)。 环游：经过一个图G的每条边至少一次的闭回路。
定理7:(必要条件) 若图G=<V,E>有H-圈,则对V的任
何非空子集S, 均有W(G-S)≤|S|, 其中W(G-S)是从G 中删去S中所有结点及与这些结点关联的边所得到的子图
的连通分支数.
证明:设C是图G的一条H-圈,则对于V的任何非空子集S,
在C中删去S中任意一个结点v1后, 则C-v1仍是连通的路, 若再删去S中的另一个结点v2, 则W(C-v1 - v 2)≤2, 若|S|=k，则删去S中的k个结点,
2.哈密顿图的判定:
1
6 2
5 3 4
定理1 (充分条件):G是至少有3个点的完全图,则G是H图.










K2
K3
K4
K5
定理2. G是简单图, 且n≥3,若对G中任一对不相邻点 u, v, 都有d(u)+d(v)≥n . 则G是Hamilton图
引理1. 设u, v是G的一对不相邻点, d(u)+d(v) ≥n. 若G+uv是H-图G是H-图.
有W(C-v1 - v 2 -...-vk)≤k, 所以
W(C-v1 - v 2 -...-vk)≤|S| . 因为C是H回路,所以它包含了G的所有结点, 即C是G的生

《离散数学》课件-第15章欧拉图与哈密顿图

《离散数学》课件-第15章欧拉图与哈密顿图

例如
彼得松图 彼得松图满足定理15.6，但不是哈密顿图。
例15.3 下图中三个图都是二部图，判断它们 哪些是哈密顿图，哪些是半哈密顿图？
G1
G2
G3
二部图与哈密顿图的关系
设二部图G=<V1，V2，E>，
|V2||V1|。若|V2||V1|+2，则
G即不是哈密顿图，又不是半哈
G1
密顿图
（1）G1=<V1，V2，E>， 互补顶点子集为V1={a,f},V2={b,c,d,e}。 则p(G1-V1)=|V2|=4，|V1|=2， p(G1-V1)>|V1|且p(G1-V1)>|V1|+1。 所以G1即不是哈密顿图，又不是半哈密顿图。
亚瑟王和他的骑士们
◼ 亚瑟王一次召见他的p个骑士，已知每一个 骑士在骑士中的仇人不超过p/2-1个。证明：能让 这些骑士围坐在圆桌旁，使每个人都不与他的仇 人相邻。
其它重要的定理
◼ 定理1 如果G是一个n（n3）阶简单图， 且n/2，则G是哈密顿图。
◼ 定理2 如果G是一个n（n3）阶完全图， 且n为奇数，则G是哈密顿图且图中有(n-1)/2个 边不相交的哈密顿回路。
穿过每一道门，通过所有房间？
15.2 哈密顿图
1859年，爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字，要求 玩游戏的人从某城市出发沿12面体的棱，通过 每个城市恰一次，最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
点的回路称为欧拉回路 定义（欧拉图和半欧拉图）
具有欧拉回路的图称为欧拉图 具有欧拉通路无欧拉回路的图称为半欧拉图 规定平凡图是欧拉图

离散数学结构第十五章欧拉图与哈密顿图

离散数学结构第十五章欧拉图与哈密顿图

第十五章欧拉图与哈密顿图15」欧拉图—、欧拉通路、欧拉回路、欧拉图、半欧拉图的定义務定义15・1通过图（无向图或有向图）中所有边一次jl仅一次行遍图中所有顶点的通路称为欧拉通路，通过图中所有边一次并且仅一次行遍所有顶点的回路称为欧拉回路。

具有欧拉回路的图称为欧拉图，具有欧拉通路而无欧拉回路的图称为半欧拉图。

从定义不难看出，欧拉通路是图中经过所有边的简单的生成通路（经过所有顶点的通路称为生成通路），类似地，欧拉回路是经过所有边的简单的生成回路。

在这里做个规定，即平凡图是欧拉图。

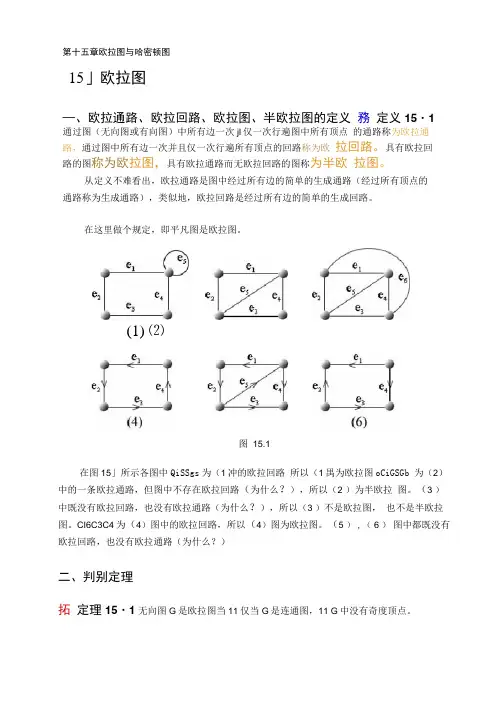
(1) ⑵图15.1在图15」所示各图中QiSSgs为（1冲的欧拉回路所以（1禺为欧拉图oCiGSGb 为（2）中的一条欧拉通路，但图中不存在欧拉回路（为什么？），所以（2 ）为半欧拉图。

（3 ）中既没有欧拉回路，也没有欧拉通路（为什么？），所以（3 ）不是欧拉图，也不是半欧拉图。

CI6C3C4为（4）图中的欧拉回路，所以（4）图为欧拉图。

（5 ） , （ 6 ）图中都既没有欧拉回路，也没有欧拉通路（为什么？）二、判别定理拓定理15・1无向图G是欧拉图当11仅当G是连通图，11 G中没有奇度顶点。

证若G是平凡图，结论显然成立，下面设G为非平凡图，设G是m条边的n阶无向图。

并设G的顶点集V ={v h v2,...,v n}.必要性。

因为G为欧拉图，所以G中存在欧拉回路，设C为G中任意一条欧拉回路，VVi,VjeV , v 都在C上，因而Vi,Vj连通，所以G为连通图。

又V Vi eV，"在C 上每出现一次获得2度，若岀现k次就获得2k度，即d(Vi)二2k ,所以G中无奇度顶点。

充分性，由于G为非平凡的连通图可知，G中边数m21.对m作归纳法。

(1) m=l时，由G的连通性及无奇度顶点可知，G只能是一个环，因而G为欧拉图。

(2) 设mwk(k21)时结论成立，要证明m二K+1时，结论也成立。

由G的连通性及无奇度顶点可知，&(G)、2•类似于例14.8 ,用扩大路径法可以证明G中存在长度大于或等于3的置，设C为G中一个圏，删除C上的全部边，得G的生成子图G,设G有s个连通分支G I,G‘2,...,G；,每个连通分支至多有k条边，且无奇度顶点，并且设G i与C*的公共顶点为, i=l,2，…,S ,由归纳假设可知，G I,G‘2，…,G；都是欧拉图,因而都存在欧拉回路Cl , i=l,2，…,s.最后将C还原(即将删除的边重新加上)，并从C上的某顶*点*开始行遍,每遇到% ,就行遍G'i中的欧拉回路Cl , i二1,2,…,s ,最后回到v r,得回路V「... ... ... "... "... b ... b ...Vr，此回路经过G中每条边一次且仅一次并行遍G中所有顶点，因而它是G中的欧拉回路(演示这条欧拉回路)，故G为欧拉图。

欧拉图于哈密顿图

欧拉图于哈密顿图
§15.1 欧拉图
一、历史背景－－哥尼斯堡七桥问题
}
1
二、定义 欧拉通路 (欧拉迹) ——通过图中每条边一次 且仅一次，并且过每一顶点的通路。 欧拉回路 (欧拉闭迹) ——通过图中每条边一次 且仅一次，并且过每一顶点的回路。 欧拉图 ——存在欧拉回路的图。
}
2
三、无向图是否具有欧拉通路或回路的判定
(3) 具有哈密尔顿回路而没有欧拉回路，
解：
(4) 既没有欧拉回路，也没有哈密尔顿回路。
解：
}
14
作业
习题十五 2、11、14、15、20
}
15
余顶点的入度均等于出度， 这两个特殊的顶点中，一个 顶点的入度比出度大1，另一 个顶点的入度比出度小1。
D 有欧拉回路( D为欧拉图) D 连通， D 中所有
顶点的入度等于出度。
}
6
例3、判断以下有向图是否欧拉图。
}
7
§15.2 哈密尔顿图
一、问题的提出
1859年，英国数学家哈密尔顿，周游世界游戏。
(2)
解：是哈密尔顿图，
存在哈密尔顿回路和通路。
}
11
例1、判断下图是否具有哈密尔顿回路，通路。
(3)
解：不存在哈密尔顿回路，
也不存在哈密尔顿通路。
}
12
例2、画一个无向图，使它
(1) 具有欧拉回路和哈密尔顿回路，
解：
(2) 具有欧拉回路而没有哈密尔顿回路， 解：
}
13
例2、画一个无向图，使它
G 中只有两个奇度 G 有欧拉通路 G 连通，
顶点(它们分别是欧拉通路的
两个端点)。
G有欧拉回路( G为欧拉图) G 连通， G 中均

离散数学PPT课件 7欧拉图与汉密尔顿图(ppt文档)

离散数学PPT课件 7欧拉图与汉密尔顿图(ppt文档)

00
0 1

1 0
11
此轮的设计:以两位二进制数
V={00,01,10,11}为结点,画带
权图(即边上标有数字--称为
边的权), 从任何a1∈V结点 画2条有向边,标权0(或1),
该边指向结点a2,于是构成 边a10, (或a11),这八条边分别 表示八个二进制数:
e0 =000
e1 =001 00 01 e5 =101 10
v2
v3
v4
v5
G2 v6
如何判定一个图中是否有 a
b
1
4
欧拉路,或有欧拉回路?
c
d
3
2
3.有欧拉路与有欧拉回路的判定: 定理8-5.1:无向图G具有欧拉路,当且仅当G是连通的,且有 零个或两个奇数度的结点. *证明:必要性, 设G有欧拉路.(自行尝试证明) 充分性,(证明的过程就是一个构造欧拉路的过程)
7. 欧拉图与汉密尔顿图
这里主要讨论图的遍历问题,一个是遍历过程中要求经过
的所有边都不同;一个是遍历过程中要求经过的所有结点
都不同.
欧拉在1736年发表了第一篇关于图论的论文, 就是就七
桥问题.
A
BDΒιβλιοθήκη CAe1 e2 e5
B e6 D
e3 e4
C
e7
一.欧拉图:
1.欧拉路:在无孤立结点的图G中,如果存在一条路,它经 过图中每条边一次且仅一次, 称此路为欧拉路.
e3 =011 e2 =010
11 1
e7 =111
000,001,010,011,100,101,110,111 从此图上取一个欧拉回路: e0e1e2e5 e3e7e6e4 将上述各边的末位数字写成序列:01011100, 于是就按照此序列将鼓轮进行加工,标0部分

欧拉图与哈密顿图

欧拉图与哈密顿图

求欧拉图中欧拉回路的算法
Fleury算法;能不走桥就不走桥
1 任取v0∈VG;令P0＝v0; 2 设Pi＝v0e1v1e2…eivi已经行遍;按下面方法来从
EGe1;e2;…;ei中选取ei+1： a ei+1与vi相关联； b 除非无别的边可供行遍;否则ei+1不应该为
Gi＝Ge1;e2;…;ei中的桥; 3当2不能再进行时;算法停止;
例15 1
例15 1 设G是非平凡的且非环的欧拉图;证明： 1λG≥2; 2对于G中任意两个不同顶点u;v;都存在简单回路C含u和v;
证明 1由定理15 5可知;e∈EG;存在圈C;e在C中; 因而pGe＝pG;故e不是桥; 由e的任意性λG≥2;即G是2边连通图;
例15 1
例15 1 设G是非平凡的且非环的欧拉图;证明： 1λG≥2; 2对于G中任意两个不同顶点u;v;都存在简单回路C含u和v;
可以验证彼得松图满足定理中的条件;但不是哈密顿图;
若一个图不满足定理中的条件;它一定不是哈密顿图;
推论
推论 设无向图G＝<V;E>是半哈密顿图;对于任意的V1V且 V1≠;均有 pGV1≤|V1|+1
证明 设P是G中起于u终于v的哈密顿通路; 令G ＝G∪u;v在G的顶点u;v之间加新边; 易知G 为哈密顿图; 由定理15 6可知;pG V1≤|V1|; 因此;pGV1 ＝ pG V1u;v ≤ pG V1+1 ≤ |V1|+1
若vi与vj有哈共密同语顿言图;就是在v能i;vj将之间图连中无向所边有vi;v顶j; 由此组成点边都集合能E;安则G排为8在阶无某向个简单初图级; 回路 vi∈V;上dvi为的与图vi有;共同语言的人数;

欧拉图和哈密尔顿图ppt课件

欧拉图和哈密尔顿图ppt课件
有欧拉通路
全部结点为偶结点， 有欧拉回路
有欧拉通路
。a
a、b、c、e
。a
全部结点为
b。 。c 都为奇结点， 。 。 。 无欧拉通路
b。
。c
d
e
f 与欧拉回路 。 。 。
偶结点， 有欧拉回路
d e f 有欧拉通路
ppt课件
8
例7-8 如图街道，是否存在一条投递线路使 邮递员从邮局a出发通过所有街到一次在回 到邮局a?
可达的：在图G中，结点u和结点v之间存在一
条路，则称结点u到结点v是可达的。
ppt课件
2
无向图的连通性
连通：在无向图G中，结点u和结点v之间存在一 条路，则称结点u与结点v是连通的。约定：任一 结点与自身总是连通的。 连通图：若图G中，任意两个结点均连通，则称G 是连通图，否则称非连通图。对非连通图可分成几
个无公共结点的连通分支。无向图中结点间的连通
关系是等价关系。 图是连通的判定法则：从图中任意一结点出发，
通过某些边一定能到达其它任意一结点，则称
图是连通的。
ppt课件
3
练习1：连通图的判定
指出下列各图是否连通
(1)
(2)
(3)
(4)
(5)
(6)
ppt课件 (7)
(8)
4
欧拉图
设G=<V，E>是连通无向图 欧拉通路：在图G中存在一条通路，经过图G 中每条边一次且仅一次。
第二节 图的连通性
通路和回路 无向图的连通性 有向图的连通性 欧拉图 哈密顿图
ppt课件
1
通路和回路 给定图G V , E
通路： G中前后相互关联的点边交替序列 w=v0e1v1e2…envn称为连接v0到vn的通路。 W中边的数目K称为通路W的长。

离散数学--第十五章 欧拉图和哈密顿图

离散数学--第十五章 欧拉图和哈密顿图
13
实例
在上图中， (1),(2) 是哈密顿图; (3)是半哈密顿图; (4)既不是哈密顿图，也不是半哈密顿图，为什么？
14
无向哈密顿图的一个必要条件
定理15.6 设无向图G=<V,E>是哈密顿图，对于任意V1V且 V1，均有 p(GV1) |V1|
证 设C为G中一条哈密顿回路。
当V1顶点在C上均不相邻时， p(CV1)达到最大值|V1|，
求图中1所示带权图k29主要内容欧拉通路欧拉回路欧拉图半欧拉图及其判别法哈密顿通路哈密顿回路哈密顿图半哈密顿图带权图货郎担问题基本要求深刻理解欧拉图半欧拉图的定义及判别定理深刻理解哈密顿图半哈密顿图的定义
第十五章 欧拉图与哈密顿图
主要内容
➢ 欧拉图 ➢ 哈密顿图 ➢ 带权图与货郎担问题
1
15.1 欧拉图
大时，计算量惊人地大
27
例6 求图中(1) 所示带权图K4中最短哈密顿回路.
(1)
(2)
解 C1= a b c d a,
W(C1)=10
C2= a b d c a,
W(C2)=11
C3= a c b d a,
W(C3)=9
可见C3
(见图中(2))
是最短的，其权为9. 28
第十五章 习题课
主要内容 欧拉通路、欧拉回路、欧拉图、半欧拉图及其判别法 哈密顿通路、哈密顿回路、哈密顿图、半哈密顿图 带权图、货郎担问题
点.
由vi 的任意性，结论为真. 充分性 对边数m做归纳法（第二数学归纳法）. (1) m=1时，G为一个环，则G为欧拉图. (2) 设mk（k1）时结论为真，m=k+1时如下证明：
5
从以上证明不难看出：欧拉图是若干个边不重的圈之 并，见示意图3.

离散数学课件15欧拉图与哈密顿图

离散数学课件15欧拉图与哈密顿图

04
欧拉图与哈密顿图的应用 场景
欧拉图的应用场景
路径规划
欧拉图可以用于表示从一 个点到另一个点的路径， 常用于物流、交通和旅行 等领域。
网络流问题
欧拉图可以用于解决最大 流和最小割等问题，在网 络优化、资源分配和计划 制定等方面有广泛应用。
组合优化
欧拉图可以用于表示组合 优化问题，如旅行商问题、 排班问题等，是求解这些 问题的常用工具。
一个图存在哈密顿回路当且仅当其所有顶点的度都大于等于2 。
哈密顿图的性质
哈密顿图中的所有顶点的度都 大于等于2。
一个图存在哈密顿回路当且仅 当其所有顶点的度都大于等于2。回 路。
哈密顿图的构造方法
添加边法
在所有顶点的度都大于等于2的图 中，不断添加边，直到所有顶点的 度都大于等于2，最后得到的图就 是哈密顿图。
哈密顿图的应用场景
社交网络分析
哈密顿图可以用于表示社交网络 中的路径，分析人际关系和信息
传播路径。
生物信息学
哈密顿图可以用于表示基因组、蛋 白质组等生物信息数据，进行基因 序列比对、蛋白质相互作用分析等。
推荐系统
哈密顿图可以用于表示用户和物品 之间的关系，进行个性化推荐和智 能推荐。
欧拉图与哈密顿图在计算机科学中的应用
欧拉图的构造方法
欧拉图的构造方法1
总结词
通过添加一条边将所有顶点连接起来， 从而形成一个欧拉图。
详细描述了两种构造欧拉图的方法， 为实际应用中构造欧拉图提供了思路。
欧拉图的构造方法2
通过将两个欧拉图合并，并连接它们 的所有顶点，从而形成一个新的欧拉 图。
02
哈密顿图
哈密顿图的定义
哈密顿图（Hamiltonian Graph）是指一个图存在一个遍历其 所有边且每条边只遍历一次的路径，这个路径称为哈密顿路径， 如果该路径的起点和终点是同一点，则称这个路径为哈密顿回 路。

离散数学欧拉图与哈密尔顿图ppt课件

离散数学欧拉图与哈密尔顿图ppt课件

例5 设G是非平凡的欧拉图，且v ∈V(G)。证明：G 的每条具有起点v的迹都能扩展成G的欧拉环游当且仅当 G-v是森林。
证明：“必要性”
若不然，则G-v有圈C。 考虑G1=G-E(G)的含有顶点v的分支H。
由于G是非平凡欧拉图，所以G1的每个顶点度数为偶数， 从而，H是欧拉图。
12
1
0.5 n 0
15
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
16
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
17
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
18
1
0.5 n 0
如果邮路图本身是非欧拉图，那么为得到行走环游，必须重 复行走一些街道。于是问题转化为如何重复行走街道？
25
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
2、管梅谷的结论
定理2 若W是图G中一条包含所有边的闭途径，则W在 这样的闭途径中具有最短的长度当且仅当下列两个条件被 满足：
在vi与vi+k间连新边ei得图G*（1≦i≦k).则G*是欧拉图， 因此，由Fleury算法得欧拉环游C.
在C中删去ei （1≦i≦k).得k条边不重的迹Qi （1≦i≦k):
E(G) E(Q1) E(Q2 )
E(Qk )

欧拉图及哈密顿

欧拉图及哈密顿
哈密顿路径是指一条遍历图的所有顶 点的路径，这条路径的起点和终点是 同一点，但路径上的边可以重复。
哈密顿图的性质
哈密顿图具有连通性，即任意两 个顶点之间都存在一条路径。
哈密顿图的顶点数必须大于等于 3，因为至少需要3个顶点才能 形成一条遍历所有顶点的路径。
哈密顿图的边数必须为奇数，因 为只有奇数条边才能形成一条闭
欧拉图及哈密顿
• 欧拉图 • 哈密顿图 • 欧拉图与哈密顿图的应用 • 欧拉回路与哈密顿回路 • 欧拉路径与哈密顿路径
目录
01
欧拉图
欧拉图的定义
总结词
欧拉图是指一个图中存在一条路径，这条路径可以遍历图中的每条边且每条边 只遍历一次。
详细描述
欧拉图是由数学家欧拉提出的一种特殊的图，它满足特定的连通性质。在欧拉 图中，存在一条路径，这条路径从图的一个顶点出发，经过每条边一次且仅一 次，最后回到起始顶点。
互作用网络的研究。
04
欧拉回路与哈密顿回路
欧拉回路的概念与性质
概念
欧拉回路是指一个图形中，从一点出 发，沿着一条路径，可以回到起始点 的路径。
性质
欧拉回路必须是连续的，不能中断， 也不能重复经过同一条边。此外，欧 拉回路必须是闭合的，起始点和终点 必须是同一点。
哈密顿回路的概念与性质
概念
哈密顿回路是指一个图形中，存在一 条路径，该路径经过了图中的每一条 边且每条边只经过一次。
随机构造法
通过随机选择边和顶点，不断扩展图，直到满足哈密顿图的条件。这种方法需要大量的计 算和随机性，但可以用于构造大规模的哈密顿图。
03
欧拉图与哈密顿图的应用
欧拉图在计算机科学中的应用
算法设计
欧拉图理论是算法设计的重要基础，特别是在图算法和动态规划 中，用于解决诸如最短路径、最小生成树等问题。

欧拉图和哈密而顿图

欧拉图和哈密而顿图
15.1 欧拉图 欧拉(1707-1783)：瑞士著名的数学家。13岁进入 欧拉 ：瑞士著名的数学家。 岁进入 巴塞尔大学， 岁取得哲学硕士学位 岁取得哲学硕士学位。 巴塞尔大学，16岁取得哲学硕士学位。1736年， 年 他证明了欧拉定理， 他证明了欧拉定理，并解决了哥尼斯堡桥的问 从而成为图论的创始人。 题，从而成为图论的创始人。 定义15.1 通过图（无向图或有向图）中每一条边 通过图（无向图或有向图） 定义 一次且仅一次行遍图中所有顶点的通路称为欧 拉通路。通过图（无向图或有向图） 拉通路。通过图（无向图或有向图）中每一条 边一次且仅一次行遍图中所有顶点的回路称为 欧拉回路。具有欧拉回路的图称为欧拉图， 欧拉回路。具有欧拉回路的图称为欧拉图，具 有欧拉通路而无欧拉回路的图称为半欧拉图。 有欧拉通路而无欧拉回路的图称为半欧拉图。
16
15.欧拉图与哈密顿图 欧拉图与哈密顿图
15.2 哈密顿图
到目前为止， 到目前为止，还没有找到哈密尔顿通路存在的充 分必要条件。下面介绍一个必要定理。 分必要条件。下面介绍一个必要定理。 定理15.6：设无向图 Ｇ＝＜Ｖ ， Ｅ＞ 是哈密尔顿 Ｇ＝＜Ｖ， 定理 ： 设无向图Ｇ＝＜Ｖ Ｅ＞是哈密尔顿 图，则对V的每个非空真子集 均成立： 则对 的每个非空真子集S均成立： 的每个非空真子集 均成立 w(G-S) ≤|S| 其中， 中的顶点数， 表示G删去 其中， |S| 是S中的顶点数， w(G-S)表示 删去 中的顶点数 表示 删去S 顶点集后得到的图的连通分图的个数。 顶点集后得到的图的连通分图的个数。
9
15.欧拉图与哈密顿图 欧拉图与哈密顿图
例：用定理解决哥尼斯堡桥的问题
15.1 欧拉图
个结点为奇次数， 有４个结点为奇次数， ∴不存在欧拉回路，也不存在欧拉路径。 不存在欧拉回路，也不存在欧拉路径。 故要从一点出发经过桥一次且仅一次的路径， 故要从一点出发经过桥一次且仅一次的路径 ， 再回到出发点是不可能的。 再回到出发点是不可能的。

22 欧拉图与哈密顿图

22 欧拉图与哈密顿图

2.若h1=G，则G是欧拉图，否则转下一步。 3.记H=G-h1，因为G是连通图，所以H与h1至少有一个节点重 合，不妨记为vi，又因为h1中d(vi)是偶数，故在H中d(vi)仍 是偶数，从而从图H的节点vi出发，重复步骤1的做法，又 可得简单回路h2: (vi,e’1,v1,e’2,…,vi)这里ei’≠ ej’(i≠j),那么h1∪ h2所对应的简单回路是：(v0,e1,v1,e2,…,vi, e1’,v1,e2’,…,vi， ei+1，…，ek+1,v0)。不妨将h1∪ h2仍记为h2，转步骤2。 对于有限图G，我们总可以在有限步骤中构造出简单回路 h1，使得h1=G，故G是欧拉图。
②现在我们来证明：若G中对于每一对不相邻的节点u，v， 有d(u)+d(v)≧n,则G是哈密顿图。因为若在G中每一对不 相邻节点u,v之间连一条无向边，得到图H，则H是n阶无 向完全图，从而H是哈密顿图，由引理，可知G是哈密顿 图。 ③由2，我们可直接推出若任一节点v满足d(v)≥n/2，则G是 哈密顿图。 例8 格雷码及其应用：构造长度为n的2进制编码的序列， 使相邻的码仅相差1位 用Qn来建模 (接下页)
例6 证明图7-35中的图没有哈密顿回路。
证明： 证明： G中没有哈密顿回路，因为G有1度顶点，即e。现 在考虑H。因为顶点a, b，d 和e 的度都为2，所以这些顶 点关联的每一条边都必然属于任意一条哈密顿回路。现在 容易看出H中不存在哈密顿回路，因为任何这样的哈密顿 回路都不得不包含4条关联c的边，这是不可能的。
解: 图G1具有欧拉回路，例如a, e, c, d, e, b, a。G2和G3都没 有欧拉回路。但是G3具有欧拉通路，即a, c, d, e, b, d, a, b。 G2没有欧拉通路。 图H2具有欧拉回路，例如a, g, c, b, g, e, d, f, a。H1和 H3都没有欧拉回路。H3具有欧拉通路，即c, a, b, c, d, b,但 是H1没有欧拉通路。

离散数学15 欧拉图与哈密顿图

离散数学15 欧拉图与哈密顿图
穿过每一道门，通过所有房间？
15.2 哈密顿图
1859年，爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字，要求 玩游戏的人从某城市出发沿12面体的棱，通过 每个城市恰一次，最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
定义（哈密顿通路和哈密顿回路） 经过图（有向图或无向图）每个顶点一次
且仅一次的通路称为哈密顿通路。 经过图每个结点一次且仅一次的回路（初
级回路）称为哈密顿回路。 定义（哈密顿图和半哈密顿图）
存在哈密顿回路的图称为哈密顿图。 存在哈密顿通路但不存在哈密顿回路的图 称为半哈密顿图。 平凡图是哈密顿图。
由两判定定理，立即可知 （4）为欧拉图， （5）、（6）即不是欧拉图，也不是半欧拉图。
例15.2（P296） v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2
◼ Fleury算法
◼ （1）任取v0V(G)，令P0=v0。 ◼ （2）设Pi=v0e1v1e2…..eivi已经行遍，则按下面
判断所示两图是否为欧拉图、半欧拉图？
无向欧拉图与无向半欧拉图的判断方法
定理15.1（无向欧拉图的判定）无向图G是欧拉图当 且仅当G是连通图，且G中没有奇度顶点。
定理15.2（无向半欧拉图的判定）无向图G是半欧拉 图当且仅当G是连通图，且G中恰有两个奇度顶点。
（1）
（2）
（3）
有向欧拉图与有向半欧拉图的判断方法
（1）
（2）
（3）
（4）
（5）
（6）
（1）（2）（3）（4）为哈密顿图 （5）为半哈密顿图 （6）既不是哈密顿图，又不是半哈密顿图。

离散数学中欧拉路径和哈密顿路径区别

离散数学中欧拉路径和哈密顿路径区别

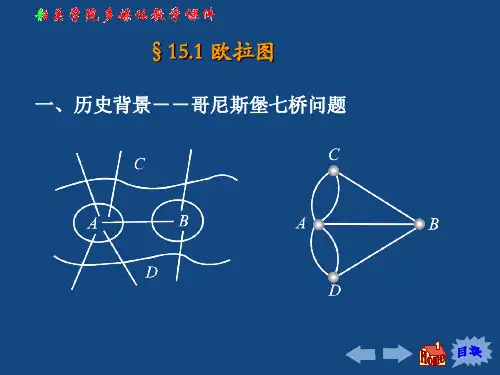
离散数学中欧拉路径和哈密顿路径区别在离散数学中，欧拉路径和哈密顿路径是图论中的两个重要概念，它们分别用于描述在图中遍历所有边或顶点的路径。

尽管它们都涉及路径的问题，但欧拉路径和哈密顿路径在定义和性质上存在着明显的区别。

接下来我们将详细介绍欧拉路径和哈密顿路径之间的不同之处。

一、欧拉路径欧拉路径是指在图中经过每条边一次且仅一次的路径，在这条路径上可以经过图中的每个顶点。

换句话说，欧拉路径是一个连通图中的路径，它包含了图中的所有边。

定义：设G=(V,E)是一个连通图，如果存在一个路径p，使得p遍历了图G的每条边一次且仅一次，则称p为图G的欧拉路径。

性质：1. 欧拉路径的存在性：对于一个连通且边数至少为1的无向图G=(V,E)，存在欧拉路径的充要条件是G是欧拉图（即G中所有顶点的度数都是偶数）或是亚欧拉图（即G中恰有两个顶点的度数奇数，其余顶点的度数都是偶数）。

2. 欧拉路径的唯一性：如果图G存在欧拉路径，那么它的欧拉路径是唯一的。

二、哈密顿路径哈密顿路径是指经过图中每个顶点一次且仅一次的路径。

换句话说，哈密顿路径是一个连通图中的路径，它包含了图中的所有顶点。

定义：设G=(V,E)是一个图，如果存在一个路径p，使得p遍历了图G的每个顶点一次且仅一次，则称p为图G的哈密顿路径。

性质：1. 哈密顿路径的存在性：判断一个图是否存在哈密顿路径是一个NP完全问题，目前没有找到确定性的多项式时间算法来解决该问题。

2. 哈密顿路径的充要条件：Dirac定理给出了判断一个有向图存在哈密顿路径的一个充要条件，即若G=(V,E)是一个有n≥3个顶点的简单图且对于任意两个不相邻的顶点u和v，有d(u)+d(v)≥n，则G中存在哈密顿路径。

结论：欧拉路径和哈密顿路径都是图论中重要的概念，用于描述图中的路径问题。

欧拉路径要求经过每条边一次且仅一次，而哈密顿路径要求经过每个顶点一次且仅一次。

欧拉路径的存在性条件相对简单，而哈密顿路径的存在性判断是一个较为困难的问题。

大学离散数学欧拉图和哈密尔顿图

大学离散数学欧拉图和哈密尔顿图

(a)
(b)
推论1:哈密尔顿图无割点.
2020/9/28
24
计算机科学学院 刘芳
15.2.3 Hamilton图的判定方法
例3：
▪ 证明下述各图不是哈密顿图。
2020/9/28
25
计算机科学学院 刘芳
15.2.3 Hamilton图的判定方法
推论2：
▪ 对二部图G＝＜ V1,V2,E＞
若| V1 |≠| V2 |，则一定不是H图。 证明：
2020/9/28
14
计算机科学学院 刘芳
15.1.4 中国邮路问题
例如：
2020/9/28
15
计算机科学学院 刘芳
15.1.4 中国邮路问题
判断条件
▪ 定理：
▪ 设L是图G的包含所有边的回路，则L具有最小长 度的充分必要条件是： ▪ 每条边最多重复一次； ▪ G的每个回路上，所有重复边的长度之和，不 超过该回路长度的一半。
2020/9/28
16
计算机科学学院 刘芳
15.2 Hamilton 图
15.2.1 问题引入 15.2.2 Hamilton图的定义 15.2.3 Hamilton图的判定方法 15.2.4 应用举例
2020/9/28
17
计算机科学学院 刘芳
15.2.1 问题引入
周游世界问题(W.Hamilton, 1859年)
▪ 可以用结点表示城市，城市间的交通路线用边表示，而 城市间的交通线路距离可用附加于边的权表示。
▪ 这样，上述问题可以归结为寻找一条权的总和为最短的 哈密尔顿回路的问题。
2020/9/28
30
计算机科学学院 刘芳
分析
▪ 穷举法 ▪ 近似算法 ▪ …………

15欧拉图与哈密顿图

15欧拉图与哈密顿图
问题转化为在图中找一条哈密顿回路. ABDFGECA即可.
哈密顿图的判定 定理1(必要条件): 设无向图G=<V, E>是哈密顿 图, V1是V的任意非空子集, 则p(G-V1)≤V1. 推论: 设无向图G=<V, E>是半哈密顿图, V1是V 的任意非空子集, 则p(G-V1)≤V1+1.
在Peterson图中, 虽然对任意顶 点集V1, 都满足p(G-V1)|V1|,但 它不是哈密顿图.
基本思想：能不走桥就不走桥
15.2 哈密顿图 定义1. 经过无向(有向)图中所有顶点恰好一次 的路(圈)称为哈密顿路(圈). 定义2. 具有哈密顿圈的图称为哈密顿图. 定义3. 具有哈密顿路但不具有哈密顿圈的图 称为半哈密顿图. 例1. 判断下列图形是否哈密顿图或半哈密顿图.
半哈密顿图 哈密顿图
都不是
例4. 判断下列有向图是否欧拉图或半欧拉图.
都不是 半欧拉图
欧拉图
一笔画问题:从某点出发,不间断地画完整个图. 即在图中找出欧拉通路（回路）.
Fleury算法: (1) 任取v0∊V(G), (2) 设Pi=v0e1v1e2eivi,
若E(G)-{e1,e2,ei}中没有与vi关联的边, 则计 算停止; 否则在vi关联的边中优先选择非桥的边 添加. (3) 令i=i+1, 返回(2).
定理2(充分条件): 设G＝<V, E>是无向简单图. 若对任意两个不相邻顶点u,vV, 均有 d(u)+d(v)|V|-1, 则G中存在哈密顿路； 若对任意两个不相邻顶点u,vV, 均有 d(u)+d(v)|V|, 则G是哈密顿图.
推论: n阶无向简单图G中, n>2, (G)n/2, 则G是
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
13
实例
在上图中， (1),(2) 是哈密顿图; (3)是半哈密顿图; (4)既不是哈密顿图，也不是半哈密顿图，为什么？
14
无向哈密顿图的一个必要条件
定理15.6 设无向图G=<V,E>是哈密顿图，对于任意V1V且 V1，均有 p(GV1) |V1|
证 设C为G中一条哈密顿回路。
当V1顶点在C上均不相邻时， p(CV1)达到最大值|V1|，
p(GV1) |V1|+1
证: 令P为G中起于u终于v的哈密顿通路，令G =G(u,v)，则G为哈
密顿图，于是
p(G’V1) |V1|
于是
p(GV1) = p(GV1(u,v)) p(G’V1) +1 |V1|+1
16
几点说明
1、定理15.6中的条件是哈密顿图的必要条件，但不是充分条件 （彼得松图） 2、常利用定理15.6判断某些图不是哈密顿图.
则G 中存在哈密顿通路.
证明：
(1) 由()证G连通 (2) = v1v2…vl 为G中极大路径. 若l = n, 证毕. (3) 否则，证G 中存在过上所有顶点的圈C，由(1) 知C外顶 点存在与C上某顶点相邻顶点，从而得比更长的路径，重 复(2) –(3) ，最后得G中哈密顿1通8 路.
第十五章 欧拉图与哈密顿图
主要内容
➢ 欧拉图 ➢ 哈密顿图 ➢ 带权图与货郎担问题
1
15.1 欧拉图
历史背景：哥尼斯堡七桥问题与欧拉图
2
欧拉图定义
定义15.1
(1) 欧拉通路——经过图中每条边一次且仅一次行遍所有顶 点的通路.
(2) 欧拉回路——经过图中每条边一次且仅一次行遍所有顶 点的回路.
(3) 欧拉图——具有欧拉回路的图. (4) 半欧拉图——具有欧拉通路而无欧拉回路的图.
11
(1)
(2)
12
哈密顿图与半哈密顿图
定义15.2 (1) 哈密顿通路——经过图中所有顶点一次仅一次的通路. (2) 哈密顿回路——经过图中所有顶点一次仅一次的回路. (3) 哈密顿图——具有哈密顿回路的图. (4) 半哈密顿图——具有哈密顿通路且无哈密顿回路的图. 几点说明： 1、平凡图是哈密顿图. 2、哈密顿通路是初级通路，哈密顿回路是初级回路. 3、环与平行边不影响哈密顿性. 4、哈密顿图的实质是能将图中的所有顶点排在同一个圈上.
地走出一条欧拉回路来？
9
Fleury算法
算法：
(1) 任取v0V(G)，令P0=v0. (2) 设Pi = v0e1v1e2…eivi 已经行遍，按下面方法从
E(G){e1,e2,…,ei }中选取ei+1： (a) ei+1与vi 相关联； (b) 除非无别的边可供行遍，否则ei+1不应该为
Gi = G{e1,e2,…,ei }中的桥.
=C(u,v) 则 为 G 中欧拉通路. 7
有向欧拉图的判别法
定理15.3 有向图D是欧拉图当且仅当D是强连通的
且每个顶点的入度都等于出度.
本定理的证明类似于定理15.1.
定理15.4 有向图D是半欧拉图当且仅当D是单向连通的，且 D中恰有两个奇度顶点，其中一个的入度比出度大1，另一个
的出度比入度大1，而其余顶点的入度都等于出度.
几点说明： 规定平凡图为欧拉图. 欧拉通路是生成的简单通路，欧拉回路是生成的简单回路. 环不影响图的欧拉性.
3
欧拉图实例
上图中，(1) ,(4) 为欧拉图，(2),(5)为半欧拉图，(3),(6) 既不是欧拉图，也不是半欧拉图. 在(3),(6)中各至少加几条 边才能成为欧拉图？
4
无向欧拉图的判别法
例2 设G为n阶无向连通简单图，若G中有割点或桥，则G不
是哈密顿图.
证 设v为割点，则 p(Gv) 2>|{v}|=1. K2有桥，它显然不是哈密顿图. 除K2外，其他有桥的图（连通的
）均有割点. 其实，本例对非简单连通图也对.
17
无向哈密顿图的一个充分条件
定理15.7ቤተ መጻሕፍቲ ባይዱ
vi,vj，
均有 ()
设G是n阶无向简单图，若对于任意不相邻的顶 d(vi)+d(vj) n1
本定理的证明类似于定理15.1.
定理15.5 G是非平凡的欧拉图当且仅当G是连通的且为若干
个边不重的圈之并.
可用归纳法证定理15.5.
8
例题
例1 设G是欧拉图，但G不是平凡图，也不是一个环，则 (G)2.
证 只需证明G中不可能有桥（如何证明？）
(1)
(2)
上图中，(1),(2)两图都是欧拉图，均从A点出发，如何一次成功
5
从以上证明不难看出：欧拉图是若干个边不重的圈之 并，见示意图3.
PLAY
6
欧拉图的判别法
定理15.2 无向图G是半欧拉图当且仅当G 连通且恰
有两个奇度顶点.
证: 必要性简单. 充分性（利用定理15.1）
设u,v为G 中的两个奇度顶点，令 G =G(u,v)
则G 连通且无奇度顶点，由定理15.1知G 为欧拉图，因而 存在欧拉回路C，令
而当V1中顶点在C上有彼此相邻的情况时，均有p(CV1) < |V1|，总
之有
p(CV1) |V1|.
而C是G的生成子图，所以有
p(GV1) p(CV1) |V1|
说明： 本定理的条件只是哈密顿图的必要条件，但不是充分条件。
可以验证彼得森图满足定理的条件，但它不是哈密顿图。
15
推论 设无向图G=<V,E>是半哈密顿图，对于任意的V1V且 V1均有
(3) 当 (2)不能再进行时，算法停止.
可以证明算法停止时所得简单通路 Pm = v0e1v1e2…emvm (vm=v0)为G 中一条欧拉回路. 用Fleury算法走出上一页图(1), (2)从A出发(其实从任何一点出发都可
以）的欧拉回路各一条.
10
15.2 哈密顿图
英国数学家哈密顿于1856年提出周游世界的问题： 若要周游世界上的二十个名城，且城与城之间只 有一条路，则能否把每一个城走且只走一次，最 后返回到原地. 该问题可以抽象为图论问题：用20个顶点分别表 示20个城市，两个顶点间的连线表示城市间的路 ，要求找一条从某点出发，经过各个顶点一次且 仅一次，最后能否返回到出发点的路线?
定理15.1 无向图G是欧拉图当且仅当G连通且无奇度数顶点.
证 :若G 为平凡图无问题. 下设G为 n 阶 m 条边的无向图. 必要性 设C 为G 中一条欧拉回路. (1) G 连通显然. (2) viV(G)，vi在C上每出现一次获2度，所以vi为偶度顶
点.
由vi 的任意性，结论为真. 充分性 对边数m做归纳法（第二数学归纳法）. (1) m=1时，G为一个环，则G为欧拉图. (2) 设mk（k1）时结论为真，m=k+1时如下证明：