离散数学第十五章欧拉图与哈密顿图

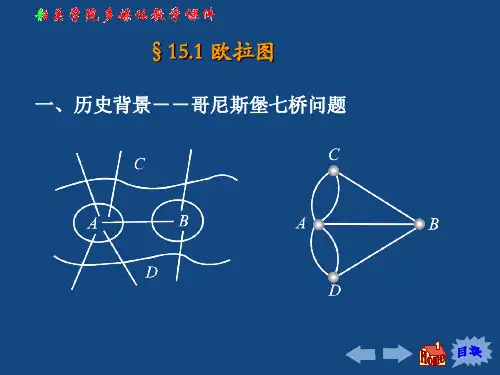
图论中的哈密顿图与欧拉图图论是数学的一个分支，研究图的性质及其应用。

在图论中，哈密顿图和欧拉图是两个重要的概念。

本文将介绍哈密顿图和欧拉图的定义、性质和应用，并探讨它们在现实生活中的实际应用。

一、哈密顿图的定义与性质哈密顿图是指一种包含了图中所有顶点的路径的图。

具体来说，哈密顿图是一个简单图，其中任意两个不同的顶点之间都存在一条路径，使得该路径经过图中的每个顶点且不重复。

哈密顿图具有以下的性质：1. 哈密顿图是一个连通图，即图中的每两个顶点之间都存在通路。

2. 图中每个顶点都是度数大于等于2的点，即每个顶点都至少连接着两条边。

二、欧拉图的定义与性质欧拉图是指一种可以通过图中每条边恰好一次的路径来穿越图的图。

具体来说，欧拉图是一个简单图，其中经过图中每条边且路径不重复的路径称为欧拉路径，而形成闭合回路的欧拉路径称为欧拉回路。

欧拉图具有以下的性质：1. 每个顶点的度数都是偶数，即每个顶点都连接着偶数条边。

2. 欧拉图中至少有两个连通分量，即图中有至少两个不同的部分可以从一部分通过路径到达另一部分。

三、哈密顿图与欧拉图的应用哈密顿图和欧拉图在实际生活中有广泛的应用，下面将分别介绍它们的应用领域。

1. 哈密顿图的应用：哈密顿图在旅行商问题中有着重要的应用。

旅行商问题是指一个旅行商要依次拜访若干个城市，然后返回起始城市，而要求找到一条最短的路径使得每个城市都被访问一次。

哈密顿图可以解决这个问题，通过寻找一条哈密顿路径来确定最短的路径。

2. 欧拉图的应用：欧拉图在电路设计和网络规划中发挥着重要的作用。

在电路设计中，欧拉图可以帮助我们确定如何安排电线的布线以最大程度地减少电线的长度和复杂度。

在网络规划中，欧拉图可以用于确定如何正确地连接不同的网络节点以实现高效的信息传输。

四、结论哈密顿图和欧拉图是图论中的两个重要概念。

哈密顿图是一种包含了图中所有顶点的路径的图，而欧拉图是一种可以通过图中每条边恰好一次的路径来穿越图的图。

离散数学中欧拉路径和哈密顿路径区别在离散数学中，欧拉路径和哈密顿路径是图论中的两个重要概念，它们分别用于描述在图中遍历所有边或顶点的路径。

尽管它们都涉及路径的问题，但欧拉路径和哈密顿路径在定义和性质上存在着明显的区别。

接下来我们将详细介绍欧拉路径和哈密顿路径之间的不同之处。

一、欧拉路径欧拉路径是指在图中经过每条边一次且仅一次的路径，在这条路径上可以经过图中的每个顶点。

换句话说，欧拉路径是一个连通图中的路径，它包含了图中的所有边。

定义：设G=(V,E)是一个连通图，如果存在一个路径p，使得p遍历了图G的每条边一次且仅一次，则称p为图G的欧拉路径。

性质：1. 欧拉路径的存在性：对于一个连通且边数至少为1的无向图G=(V,E)，存在欧拉路径的充要条件是G是欧拉图（即G中所有顶点的度数都是偶数）或是亚欧拉图（即G中恰有两个顶点的度数奇数，其余顶点的度数都是偶数）。

2. 欧拉路径的唯一性：如果图G存在欧拉路径，那么它的欧拉路径是唯一的。

二、哈密顿路径哈密顿路径是指经过图中每个顶点一次且仅一次的路径。

换句话说，哈密顿路径是一个连通图中的路径，它包含了图中的所有顶点。

定义：设G=(V,E)是一个图，如果存在一个路径p，使得p遍历了图G的每个顶点一次且仅一次，则称p为图G的哈密顿路径。

性质：1. 哈密顿路径的存在性：判断一个图是否存在哈密顿路径是一个NP完全问题，目前没有找到确定性的多项式时间算法来解决该问题。

2. 哈密顿路径的充要条件：Dirac定理给出了判断一个有向图存在哈密顿路径的一个充要条件，即若G=(V,E)是一个有n≥3个顶点的简单图且对于任意两个不相邻的顶点u和v，有d(u)+d(v)≥n，则G中存在哈密顿路径。

结论：欧拉路径和哈密顿路径都是图论中重要的概念，用于描述图中的路径问题。

欧拉路径要求经过每条边一次且仅一次，而哈密顿路径要求经过每个顶点一次且仅一次。

欧拉路径的存在性条件相对简单，而哈密顿路径的存在性判断是一个较为困难的问题。