北师大版七年级数学4.2 比较线段的长短学案作业

《比较线段的长短》作业设计方案（第一课时）一、作业目标通过本次作业，学生应能够掌握线段长短的比较方法，包括图形的直观比较、利用刻度尺等工具的测量比较以及理解基本原理的掌握，通过实际应用练习提高学生的计算能力，达到知识的运用自如。

二、作业内容本课时作业旨在让学生在不同场景下学习比较线段的长短，培养学生对图形的理解和分析判断能力。

作业内容包括以下几个部分：1. 课本知识点复习：重温线段定义和长短比较的基础理论，并强调比较线段长短的基本原则。

2. 基础练习：提供一系列的线段图形，要求学生直接观察并比较线段的长短。

3. 测量实践：使用刻度尺等工具对实际生活中的线段进行测量，并比较其长短。

4. 情景应用：设计不同情景下的线段比较问题，如道路长度比较、图形周长计算等。

5. 自我探究：提供一定量的开放式问题，引导学生自行探究不同方法的线段长短比较方式。

三、作业要求作业要求如下：1. 基础练习和测量实践部分，要求学生在理解的基础上完成线段的长短判断，注重培养学生的逻辑思维能力和空间感知能力。

2. 情景应用部分，要求学生将所学知识应用到实际问题中，提高学生的问题解决能力。

3. 自我探究部分，鼓励学生自主思考、尝试多种方法解决问题，培养学生的创新意识和自主学习能力。

4. 作业过程中需注意单位统一和测量准确，避免因单位不统一或测量误差导致的结果错误。

5. 完成作业后需进行自我检查和修正，确保答案的准确性。

四、作业评价作业评价将从以下几个方面进行：1. 准确性：评价学生答案的正确性，是否能够准确判断线段的长短。

2. 逻辑性：评价学生的解题思路是否清晰，是否能够合理运用所学知识解决问题。

3. 创新性：评价学生在自我探究部分的表现，是否能够提出新的解题思路和方法。

4. 规范性：评价学生的作业书写是否规范，是否符合数学学科的要求。

五、作业反馈作业反馈是提高学生自主学习能力的重要环节，教师应及时对学生的作业进行评价和反馈，指出学生的不足之处和需要改进的地方，同时也要肯定学生的优点和进步，鼓励学生继续努力。

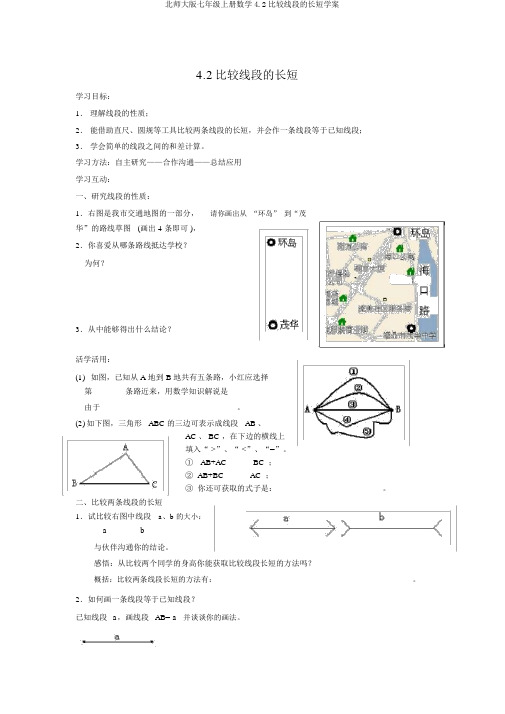
4.2比较线段的长短学习目标：1．理解线段的性质；2．能借助直尺、圆规等工具比较两条线段的长短，并会作一条线段等于已知线段；3．学会简单的线段之间的和差计算。

学习方法：自主研究——合作沟通——总结应用学习互动：一、研究线段的性质：1．右图是我市交通地图的一部分，请你画出从“环岛” 到“茂华”的路线草图(画出 4 条即可 )，2．你喜爱从哪条路线抵达学校？为何？3．从中能够得出什么结论？____________________________________活学活用：(1)如图，已知从 A 地到 B 地共有五条路，小红应选择第 _______条路近来，用数学知识解说是由于 ______________________________ 。

(2)如下图，三角形 ABC 的三边可表示成线段 AB 、AC 、 BC ，在下边的横线上填入“ >”、“ <”、“=”。

①AB+AC______BC ；② AB+BC______AC ；③你还可获取的式子是： ______________________ 。

二、比较两条线段的长短1．试比较右图中线段a、b 的大小：a_______ b与伙伴沟通你的结论。

感悟：从比较两个同学的身高你能获取比较线段长短的方法吗？概括：比较两条线段长短的方法有：_________________________________________ 。

2．如何画一条线段等于已知线段？已知线段a，画线段AB= a并谈谈你的画法。

概括： ____________________________________________.活学活用：(1) 依据线段的长短， 能够进行线段之间的和差计算。

如右图：点 C 、D 在线段 AB 上，填空：① AD=______ + _______ ；② CD=B C － ______；③ BD=A B －_____=_____－ CD※方法总结：确立线段的和差的方法是：察看点各点在同向来线上的相对地点。

第二节 比较线段的长短【学习目标】 1.理解线段公理。

2. 线段长短的比较。

3.认识线段的中点。

【学习重难点】1.会用测量法和重叠法来比较线段的长短。

2. 认识线段的中点。

【学习方法】小组合作学习。

【学习过程】模块一 预习反馈一、知识回顾1、绷紧的琴弦、人行横道线都可以近似地看做 。

线段有 个端点。

2. 可表示为线段 （或） 或者线段______二、自主学习（P110—111）分组活动一：讨论问题1问题1如图，从小明家到学校共有三条路小明为了尽快到学校，应选择第 ＿＿条路，为什么？结论：（1）线段公理：两点之间得所以连线中， 最短。

（2）两点之间的距离：两点之间线段得 叫做这两点之间的距离。

分组活动二：阅读教材110页，思考问题，完成“议一议”。

小组讨论，总结比较线段长短的方法。

1方法一比较两线段的长短可以先分别用刻度尺度量出 的长度，然后按 比较两线段的长短，线段的长短关系和他们的长度大小关系是一致的。

即时演练aA B1．如何比较两位同学的身高？① 如果已知身高，我们如何比较？② 如果不知身高，我们又如何比较？2.如下图所示的两条线段CD 、EF ，先目测一下它们的大小，再利用现有的工具，想出一种很快的比较出它们的大小的方法，与自己刚才的目测结果进行比较，你会发现什么呢？2，方法二： 将其中一条线段移到另一条线段上去，将其中的一个端点 在一起加以比较。

结果有三种情况： ， ， 。

① 如果点D 与点B 重合，就说线段AB 与线段CD 相等，记作 AB=CD ，如图： ② 如果点D 在线段AB 内部，就说线段AB 大于线段CD ，记作AB>CD 如图：③如果点D 在线段AB<CD ，如图：3. 画一画1、已知线段AB ，用直尺和圆规画一条线段OA ，使它等于已知线段AB 。

请说说你的画法.如图点A 是线段AB 的中点，则几条线段之间的关系是 = =21 。

（或 = =2 。

）若一点把一条线段分成 的两条线段，那么这个点就叫做这条线段的中点模块二 合作探究A BO C DE F A(C) B(D) · · A(C) D B· · · A(C) B D · · ·例：2、如果线段AB=5cm,BC=3cm,那么A,C两点间的距离是实践练习：已知直线l上有A、B、C三点，且线段AB=4cm，线段BC=3cm，如果点O是线段AC 的中点，求线段OB的长。

新北师大版七年级数学上册学案：4.2比较线段的长短学习内容:比较线段的长短教学设计 (收获)二、小组学习 [来源:学&科&网]已知线段AB=10cm,在直线AB 上有一点C ，BC=4cm,点M 是线段AC 的中点，试计算线段AM 的长。

三、展示反馈：（展示你的风采） [来源:Z §xx §]1)已知线段a.b 求作一条线段c,使c=a+b2)在直线l 上顺次取A.B.C 三点，使得AB=6cm,BC=2cm,如果O 是线段AC 的中点，求线段AO,BO,CO.的长。

( 画出图形)上题中AO+BO= cm=线段 的长，AO+OC= cm=线段 的长。

AB-OA= cm- cm= cm =线段 的长。

BC=线段 —线段 。

[来源学科网]3）在直线l 上有A.B.C 三点顺次排列，已知AB=3cm,BC=8cm,M.N 分别为AB.BC 的中点，画出图形，并求出MN 的长。

学习目标：能借助于尺、规等工具比较两条线段的大小并作一条线段等于已 知线段重点 ：比较两条线段的大小并作一条线段等于已知线段 难点： 作一条线段等于已知线段自主学习:（相信你一定行﹗）一、认真阅读课本P 110页议一议上面的内容，解决下列问题：1、观察此页的第一个图，从A 地到C 地有 ______条道路，______条道路最近，可得结论简称为 ___________________________。

2、若已知线段AC 的长度为5cm ，则点A 与点C 之间的距离为____cm 。

二、认真阅读课本P 110页议一议下方的内容，解决下列问题：1、如下图所示，线段AB 与线段CD 的长短关系为_______________，若要比较线段AB 与线段CD 的长短，你有哪些方法？2、模仿例题：已知线段a,用尺规作一条线段AB ，使线段AB = a （写出作法） a教学反思 （疑惑）baA BC D3、如右图所示，点C、D在线段AB上，则AB = AC + ____， CD = AD - ____；若C是线段AD的中点，则AC = _____ = ______。

4.2比较线段的长短导学案学习目标：能借助直尺、圆规等工具，比较两条线段的长短。

能用圆规作一条线段等于已知线段。

重点：了解线段性质及比较方法，两点之间的距离的概念和线段中点的概念。

难点：比较线段长短的方法，线段中点的表示方法和应用。

学习过程：课前热身：辨别直线、射线、线段，并能用不同的方法表示它们．自主学习：阅读课本110-111页内容，完成下列问题，1.在地面上有两点A 和C ，C 处放有一块骨头，三只不同颜色的小狗从A 点跑到C 点吃骨头，所经过的路线不同，请同学们辨别，哪只狗更聪明．结论：____________________________________________________2．探究：比较线段的长短怎样比较两根筷子的长短．方法：___________________3．探究：作一条线段等于已知线段方法：___________________4．探究：线段的中点线段的中点的定义：____________________________因为点M 在线段AB 上,M 是AB 的中点所以 AM=_____=________或AB=________=________.反馈检测：判断：1．两点之间的线段叫做这两点间的距离 （ ）2．如果点C 是线段AB 的中点，那么AC CB = （ ）3．如果AC CB =，那么点C 是AB 的中点 （ ）选择：1．两点之间线段的长度是（ ）A ．线段的中点B ．线段最短C ．这两点间的距离D ．线段的三等分点2．在跳绳比赛中，要在两条长度相近的绳中挑选一条最长的绳子参加比赛，最简单的选择方法是（ ）A ．把两根绳子接在一起B ．把两条绳子一端对齐，然后拉直两条绳子，另一端在外面的即为长绳 AB MC．用尺量绳长D．没有办法挑选实践应用1．有一弯曲的灌渠流经一片农田，为了缩短流程，以减少分水的过分流失，现要将该灌渠改直，请问这应用的是什么结论？2.如图，点C是线段AB上的一点，点M是线段AB的中点，点N是线段BC的中点．（1）如果10cmAB=，3cmAM=，求NC的长．（2）如果6cmMN=，求AB的长．布置作业：4.2知识技能1, 2 , 3 学习反思：A BM C。

4.1比较线段的长短导学目标1、线段的性质：两点之间，线段最2、掌握比较线段长短的两种方法3、会用直尺和圆规画一条线段等于已知线段4、理解线段和、差的概念及画法。

5、理解两点间距离的概念和线段中点的概念及表示方法，学会线段中点的简单应用导学重点：线段长短的两种比较方法导学难点： 对线段与数之间的认识，掌握线段比较的正确方法 温故：线段的定义链接：两只长短不同的筷子如何比较它们的长短？比较长短的关键是什么？ 新知一、线段的性质及两点之间的距离的教学1、 阅读课本139页，思考小猫与小狗为何走课本所示的路线，这说明了什么问题？2、 什么叫做两点之间的距离？二、如何比较线段长短的教学 画出AB 、CD 两条线段。

（长短不一） 1．“议一议” 怎样比较两条线段的长短？叠合法：把线段AB 、CD 放在同一直线上比较，步骤有三： ① 将线段AB 的端点A 与线段CD 的端点C 重合 ② 将线段AB 沿着线段CD 的方向落下③ 若端点B 与端点D 重合，则得到线段AB 等于线段CD ，可记做：AB=CD （几何语言）若端点B 落在D 内，则得到线段AB 小于线段CD ，可记做：AB ＜CD若端点B 落在D 外，则得到线段AB 大于线段CD ，可记做：AB ＞CD 如图12度量法：用刻度尺分别量出线段AB 和线段CD 的长度，再将长度进行比较。

三、如何用圆规做一条线段等于已知线段及线段的和差A CD1、已知线段a （如图），用直尺和圆规画一条线段，使它等于已知线段a 。

a2、已知线段a 、b ，画一条线段c ，使它的长度等于已知线段的长度的和。

3画一条线段d ，使它的长度等于已知线段的长度的差四、线段中点的教学阅读课本140页明确线段中点的定义 定义：用几何语言表示：∵点C 是线段AB 的中点∴ AC=BC=12 AB （或AB=2AC=2BC ）对应练习：（1）填空：如图D已知点C 是线段AB 的中点，点D 是线段AC 的中点，①AB= BC ②BC= AD ③BD=_____AD（2）P C D例题：如上图，点P 是线段的中点，点C 、D 把线段AB 三等分。

4.2 比较线段的长短【学习目标】1.了解“两点之间线段最短”的性质；2.能借助直尺、圆规等工具比较两条线段的长短，并能用圆规作一条线段等于已知线段；3.理解线段中点的概念，会用数量关系表示中点及进行相应的计算．【预习】1. 两点之间的所有连线中，_________最短.2. _______________________________叫做两点之间的距离.3. 点M把线段AB分成两条相等的线段，点M就叫做线段AB的_______，这时，AM = BM =_______ AB（或AB= _ _ _ _ AM = _ _ _ _ BM）.【预习反馈】1. 下列说法正确的是（）A. 两点之间的连线中，直线最短B.若P是线段AB的中点，则AP=BPC. 若AP=BP, 则P是线段AB的中点D. 两点之间的线段叫做者两点之间的距离2. 已知点C是线段AB上的一点，M，N分别是线段AC,BC的中点，则下列结论正确的是（）A. MC=12AB B. NC=12AB C.MN=12AB D.AM=12AB3.如果线段AB=5 cm,线段BC=4 cm,那么A,C两点之间的距离是（）A. 9 cmB.1 cmC.1 cm或9 cmD.以上答案都不对【合作探究】情境引入如何比较两名同学的身高呢？你有哪些方法呢？讲授新知线段的性质（公理）、两点之间的距离活动1例1如图所示，直线MN表示一条铁路，铁路两旁各有一点A和B，表示两个工厂．要在铁路上建一货站，使它到两厂距离之和最短，这个货站应建在何处？注：(1)两点之间的距离的概念描述的是数量，而不是线段本身．(2) 在解决选择位置、求最短距离等问题时，通常转化为“两点之间线段最短”思考1：如何比较两条线段的长短？方法有哪些？思考2：如何借助尺规画一条线段等于已知线段？活动2例2如图，已知线段AB，用尺规作一条线段等于已知线段AB.跟踪训练1：已知线段a、b，画一条线段AB，使AB=a+b.思考：如图，已知线段a、b，求作线段AB，使c＝b-a.（不写作法，保留作图痕迹）.思考3：如何找到一条绳子的中点呢？线段的中点定义是什么？例3如图,AB=20 cm，C是AB上一点，且AC=12 cm，D是AC的中点，E是BC的中点，求线段DE的长.解：∵AB=8 cm，CB=5 cm∴AC=______-_______ (表示出线段和差)=__________∵D是AC的中点∴DC=_______=_______活动3 思维拓展已知线段AB＝10 cm，直线AB上有一点C，BC＝6 cm，M 为线段AB的中点，N为线段BC的中点，求线段MN的长.课堂小结：本节课你学到了什么？作业布置（A组）运用分类讨论思想求线段的长度已知A，B，C三点在一条直线上，且线段AB＝15 cm，BC＝5 cm，D为线段AC的中点，E为线段AB的中点，求线段DE的长.(B组)课本课后作业第3、4题。

《比较线段的长短》作业设计方案（第一课时）一、作业目标通过本次作业，学生应能够掌握线段长短的比较方法，包括直接观察法、度量法以及几何推理法等，能够正确理解和运用相关数学概念，提升空间想象能力和数学思维。

二、作业内容1. 基础知识巩固：学生需熟练掌握线段的基本概念及表示方法，理解线段长短的直观比较方法。

2. 操作练习：通过画图、量度等实际操作，学生应能自主比较线段的长度。

在纸上任意画出两条线段，利用直尺和刻度尺量出其长度，并记录下量度结果，用语言表达其长短关系。

3. 拓展练习：根据已学的数学知识，分析解决较为复杂的比较线段长度的问题。

包括对实际问题的观察与测量，运用图形分析，判断线段的相对长短。

4. 小组合作：以小组形式开展讨论，组内成员互相出题、解答、验证比较线段长度的题目，分享不同的解题思路和方法。

三、作业要求1. 作业应在规定时间内独立完成，要求字迹清晰、步骤完整。

2. 画图部分需使用直尺等工具辅助，保证图形准确无误。

3. 量度时注意使用刻度尺的正确方法，保证量度结果的准确性。

4. 操作和拓展练习部分应详细记录过程和结果，并在小组讨论中积极发言。

5. 小组合作过程中应积极参与、相互学习、共同进步。

四、作业评价1. 作业准确率：检查学生对知识点的掌握程度及运用情况。

2. 操作规范性：评价学生是否规范操作、细心完成量度及画图任务。

3. 解题思路：评价学生的解题思路是否清晰、灵活运用所学知识。

4. 小组合作：评价学生在小组讨论中的表现及合作精神。

五、作业反馈1. 教师批改：教师对学生的作业进行批改，指出错误并给出正确答案及解题思路。

2. 学生自评与互评：学生自我评价及小组内成员互相评价，反思自己在作业中的表现及学习成果。

3. 针对共性问题进行讲解：针对学生在作业中普遍存在的问题进行讲解和指导，帮助学生更好地掌握相关知识点。

4. 鼓励与激励：对表现优秀的学生给予表扬和鼓励，激发学生的学习积极性和自信心。

4.2比较线段的长短知识点一：两点之间的所有连线中，线段最短知识点二：借助直尺.圆规等工具比较两条线段的长短。

知识点三：用圆规作一条线段等于已知线段。

一.预学质疑（设疑猜想.主动探究）1.下列各种图形中，可以比较大小的是（ ）A.两条射线B.两条直线C.直线与射线D.两条线段2.如图所示,小明到小颖家有三条路，小明想尽快到小颖家,那么他应该选择第_____条，理由是 。

3.比较下列各组线段的长短（用“>”，“<”或“=”填空）图2图1（1）如图1，线段OA 线段OB ； （2）如图2，线段AB 线段AD . （2）如图3，线段AB 线段AC 线段BC ； 4.如图，若点C 是线段AB 的中点，那么_____21_____==AC ，_____2_____2==AB 。

要做学疑之星，提价值性问题：阅读课文内容，你认为模糊或不懂的地方记录下来：二.研学析疑（合作交流.解决问题）1. 线段大小的比较方法（1）观察法；（2）叠合法；（3）度量法。

2.尺规作图，一条线段等于已知线段。

如图，已知线段AB ，用尺规作一条线段等于已知线段AB 。

解：变式训练：已知线段b a ,（如图），画出线段AB ，使AB=b a 2+3.线段的中点. 图形语言：文字语言：∵点M 是线段AB 的中点符号语言：∴ 或 4.线段中点的运用【例题1】如图、已知：线段AB =10cm ，C 为AB 的中点，求AC 的长．【例题2】如图，点C 是线段AB 上的点，点D 是线段BC 的中点，若AB =10，AC =6，求CD 的长。

【例题3】如图．线段AB =8cm ，点C 是线段AB 上任意一点，若M 为AC 的中点，N 为BC 的中点，求MN 的长．三.导法展示(巩固升华.拓展思维)1.如果点B 在线段AC 上，那么下列各表达式中：①AC AB 21=，②BC AB =，③AB AC 2=，④AC BC AB =+，能表示B 是线段AC 的中点有( )。

比较线段的长短（学案）
姓名_______________
【我的目标】
1、会画一条线段等于已知线段；
2、掌握线段长短比较的一般方法，会用几何语言表示两线段之间的大小关系；
3、理解线段中点的含义。

4、了解线段最短公理：两点之间，线段最短
【探索新知】
活动一：
线 段AB=_______________cm
折 线AB=_______________cm
例题：已知线段a ，用没有刻度的直尺和圆规作一条线段等于已知线段a. a 画法：① 作射线AB;
② 用圆规量出已知线段的长度(记作a);
③ 在射线AB 上截取AC = a .
练习：已知线段AB 与线段CD ，利用两种不同的方法比较它们的长短
方法一：（度量法） 方法二：（叠合法）
活动二：认识中点
定义：点M 把线段AB 分成相等的两条线段AM 与BM ，点M 叫做线段AB 的_______________
AM=BM=_____________ AB ＝2_________＝2_________
【自我评价】请你根据本节课知识掌握的情况，给它添上嘴巴吧！
A
B C D B A B。