大学物理-旋转矢量

旋转矢量法在简谐振动中的应用探讨摘要：结合旋转矢量法的理论依据探究旋转矢量法在简谐振动中的应用，探究结果发现：旋转矢量法的理论依据是两个振幅相等，频率相同的简谐振动，相位差等于π/2，沿垂直方向的合成就是圆周运动；而旋转矢量法可计算简谐振动的矢端速度与加速度、相位与初相位、运动时间间隔及合振动。

关键词：旋转矢量法；简谐振动；应用0.旋转矢量法旋转矢量法[1]，也叫匀速圆周运动法，参考圆法，用其方法来解决简谐振动中的问题，相对来说比较简单。

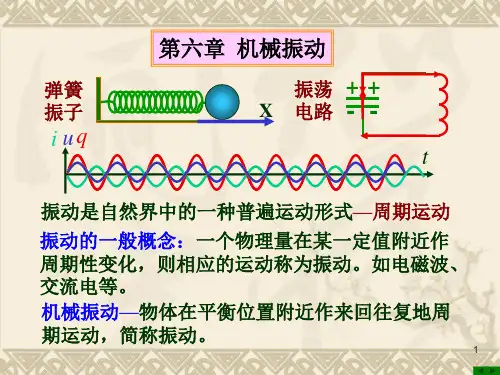
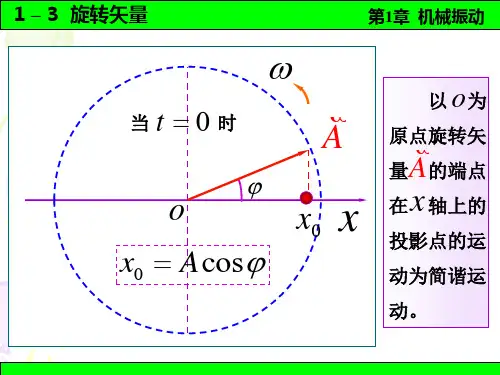
如图1，做一个圆周，以O为原点，向右为正方向建立坐标轴，根据题目条件确定半径位置，要观察的是半径的端点在x轴上的投影的位置，如果速度为正，半径端点一定处于x轴下方，反之在x轴上方，比如，t＝0时，质点正经过平衡位置向正方向运动，那么这个半径端点就是在原点正下方，即端点的投影刚好在原点[2]。

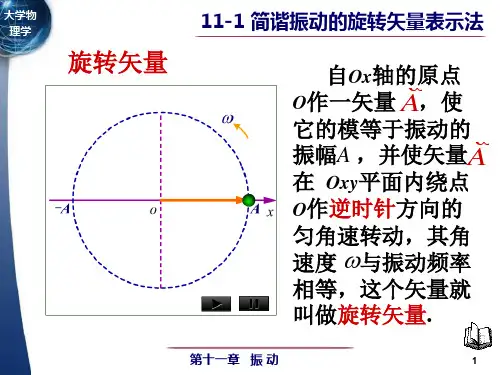
而以O为原点的旋转向量A的端点与在x 轴上的投影点的运动为简谐振动。

图1 旋转矢量图2 相位差为π/2互相垂直简谐振动的合成1.简谐振动矢量法的理论依据互相垂直相同频率简谐振动的合成[3]，现将分振动的运动学方程表示为，，质点既沿Ox轴又沿Oy轴运动，实际上是在Oxy平面上运动。

从上面方程消去t，得合振动的轨迹方程：=。

当相位差为时，，表明合振动的轨迹为以x和y为轴的椭圆，如图2所示这里又可分为两种情况，时，x方向的振动比y方向的振动超前，即，当某一瞬时，则x=0，y=A2，即质点在图2(a)中的P点，经过很短时间后略大于零，y将略小于A2，为正，而略大于，x将为负，故质点运动到第二象限，即质点沿椭圆逆时针运动。

反之，时，y方向的振动比x方向的振动超前，质点沿椭圆顺时针方向运动，如图2（b）。

以上两分运动中，若=且相位差为，则其合运动轨迹方程褪化为圆。

两个振幅相等，频率相同的简谐振动，相位差等于沿互相垂直方向合成的为圆周运动；反推理可得，圆周运动亦能分解为两互相垂直的同振幅同频率的简谐振动。

大学物理旋转矢量（一）引言概述：在大学物理的学习中，旋转矢量（一）是一个重要的知识点。

旋转矢量是描述物体在空间中旋转运动的工具，它具有方向和大小，并可以表示绕定轴进行的旋转。

本文将围绕旋转矢量展开讨论，依次讲解旋转矢量的基本概念、旋转轴和角速度、刚体的定点转动、角动量和力矩、以及旋转的动力学方程。

一、旋转矢量的基本概念1. 旋转的定义与描述2. 旋转角度的表示方法3. 旋转矢量的含义与性质4. 旋转矩阵的使用及推导5. 旋转矢量与坐标系的转换二、旋转轴和角速度1. 旋转轴的定义与求解2. 旋转轴的方向确定方法3. 角速度的概念与计算4. 角速度的单位及数值表达5. 转动矢量与角速度的关系三、刚体的定点转动1. 定点转动的定义与特点2. 转动惯量的概念与计算3. 定点转动的动力学方程4. 定点转动的动力学矢量关系5. 刚体定点转动现象的实例分析四、角动量和力矩1. 角动量的概念与性质2. 角动量的计算与单位3. 力矩的定义与计算4. 力矩的性质与作用5. 角动量和力矩的关系及应用五、旋转的动力学方程1. 旋转的动力学定律与原理2. 牛顿第二定律在旋转运动中的应用3. 旋转的动力学方程的推导过程4. 动力学方程与运动学方程的对应关系5. 旋转动力学方程实际问题的解析解和数值解总结：通过本文的介绍，我们对大学物理中的旋转矢量有了更深入的认识。

我们了解到旋转矢量的基本概念、旋转轴和角速度的计算方法、刚体的定点转动特性、角动量和力矩的关系，以及旋转的动力学方程的应用。

这些知识将有助于我们理解旋转运动的本质和规律，为进一步的学习和研究打下了基础。

引言概述：在大学物理学中，旋转矢量（二）是一个重要的概念。

它在描述物体旋转和角动量时发挥着关键作用。

本文将详细阐述旋转矢量的相关内容，包括其定义、性质以及在实际应用中的应用案例等。

正文内容：一、旋转矢量的定义1.旋转矢量的概念和来源2.旋转矢量的数学表示和坐标系选择3.旋转矢量的物理意义和几何解释4.旋转矢量与旋转矩阵的关系5.旋转矢量的性质和基本运算法则二、旋转矢量的旋转定理1.旋转矢量的定义和旋转方向2.旋转定理的几何解释和物理意义3.旋转定理的数学推导和证明4.旋转定理的应用案例：刚体的旋转运动5.旋转定理的实验验证和实际应用三、旋转矢量的角动量1.角动量的定义和物理性质2.角动量的计算方法和表达式3.角动量守恒定律和旋转矢量的关系4.角动量的变化和影响因素5.角动量对物体运动轨迹的影响和解释四、旋转矢量的应用案例1.旋转矢量在力学和动力学问题中的应用2.旋转矢量在电磁学和光学问题中的应用3.旋转矢量在量子力学和粒子物理学问题中的应用4.旋转矢量在天体力学和宇宙学问题中的应用5.旋转矢量在工程和技术领域中的实际应用五、旋转矢量的拓展与发展1.旋转矢量的局限性和扩展性2.旋转矢量在现代物理学和数学中的发展趋势3.旋转矢量在计算机图形学和虚拟现实领域中的应用4.旋转矢量的研究方法和实验手段5.旋转矢量相关学科和概念的比较和关联总结：旋转矢量作为大学物理学的重要内容，在描述物体旋转和角动量时具有不可替代的作用。

本文从旋转矢量的定义、性质和旋转定理开始，详细阐述了其在实际应用中的案例和应用领域。

同时，展望了旋转矢量的拓展与发展，以及与其他学科和概念的比较与关联。

通过对旋转矢量的深入研究和理解，有助于我们更好地理解物体的旋转规律和角动量的变化，为解决各种实际问题提供了强有力的工具和方法。

引言概述：旋转矢量是大学物理中一个重要概念，它在描述物体或系统的旋转运动中起到了关键作用。

本文将从基本概念出发，分析旋转矢量的定义、性质和应用，并探讨其在物理学中的重要性。

大学物理学教学中初相位的求解——旋转矢量法
初相位的求解作为理论物理学中一个重要的内容经常被大学物理学教学中提及，相比较传统的三角函数法，旋转矢量法作为一种新的数学计算方式正逐步在各个大学物理教学中得到应用，本文将以此方式进行初相位的求解及应用。

旋转矢量法是一种计算变换位置、旋转之间关系的重要方法，可以把旋转视为矢量，这种矢量可以是旋转轴向量乘以旋转角度的形式。

在计算初相位时，可以利用旋转矢量的相加、相减，从而得出相应的位置、角度变换及旋转信息，从而解决初相位求解问题。

旋转矢量法具体应用于初相位求解时如下：
（1）以坐标系0-A，以A点为原点，以X轴为横轴，以Y轴为纵轴。

（3）从A点到B点的位移量为Rb，定义α角为旋转量，此旋转的旋转轴向量为：
U=(X`Y`Z`)。

（5）根据位移量Ra和α角，计算出旋转矢量：〖R_b〗^α=(X^`Y^`Z^`)。

（6）由计算出的旋转矢量〖R_b〗^α和位移量Ra，求出从A点到B点的旋转量Φ：Φ=〖R_a〗^α+Ra，Φ即为A点到B点的初相位。

（9）根据计算出的β角得出从A点到B点的旋转量γ：γ=β- α。

以上就是应用旋转矢量法求出初相位的步骤，3D旋转的运算角度可以根据同理求出。

传统的三角函数法只能表示2D的运算，而旋转矢量法则不仅可以求出2D的运算，还可以求出3D的运算，可以用来解决复杂的初相位求解问题。

总之，旋转矢量法作为一种基于几何的运算方式，其优点可以体现在于它融合几何和代数在一起，能够有效解决复杂多轴的位移、角度变换及旋转运算的问题，可以有效求解初相位问题。

从而为进一步的理论物理数学研究打下基础。

P H ASE OF FO R CED VIBRATI O N BY R OTATING VECTO RXu You w en Xu D i yu( D epa r t ment of Physics , S ichua n Vocatio n al and Technical College , S ui n i n g , S ichuan 629000)Abstract A cco r d i n g to t h e dyna m ic a n d ki n e matic equatio n s of fo r ced vi b ratio n , t h e a mp li2 t u de a n d i n itial p h a s e of fo rce d vi b ratio n a r e o b t a i n ed .K ey Words fo rced vi b ratio n ; ro t a ti n g vecto r ; a m p lit u de ; i n itial p ha s e系统在周期性外力作用下被强迫进行的振动,称为受迫振动. 受迫振动是工程技术中常见的振动. 研究受迫振动具有很大的意义. 求解受迫振动达到稳定状态时的振幅和初相, 一般书籍[ 1～6 ] 都是通过求解受迫振动的动力学方程而得出的,本文用旋转矢量法求受迫振动的振幅和初相.图 1受迫振动的动力学方程旋转矢量受迫振动所受的作用力有:准弹性力- k x 、如图1 所示,从O x坐标轴的原点O , 作一矢量 A ,其长度A 等于谐振动的振幅; t = 0 时 A 与O x 轴夹角等于初相φ; 并使 A 以大小等于谐振动角频率ω的角速度, 沿逆时针方向匀速转动, 这个矢量A 就称为旋转矢量.旋转矢量法是直观地研究谐振动的几何方法. 它不仅可以帮助人们形象地了解谐振动各物理量的含义及其相互关系, 而且便于对谐振动进谐激励力F0 co sωt 、与速度成反比的阻尼力- cv 因此,作受迫振动物体所受的合力为+ F0 co sωt -F = - k x由牛顿第二定律,得cv2md x= - k x + F0 co sωt - cv2d t2d x= - k x +F0sωt - c v∴d t2m m m取ω2 = k/ m ,2β= c/ m , f 0 = F0 / m ,并注意v =d x,0 d t代入上式得受迫振动的动力学方程为d2 x d x2+ 2βd t+ ω0 x = f 0 co sωt(1)d t2这是一个非齐次的常系数二阶微分方程.它的通解为A 0e -βt co s( 0 - β2 t + φ0 )ω2+ A c o s(ωt - δ)x =经过足够长的时间后, 其中第一项解减弱到可以忽略不计,只有第二项是振幅不变的振动.因此,受迫振动达到稳定状态时的运动学方程为[ 7]图 2作H G ⊥O G,在Rt △O G H 中,x = A c o s(ωt - δ)(2)F2 = ( B - D) 2 + C2式中A 是受迫振动稳态时的振幅;角频率等于简谐激励的角频率ω;δ是稳态响应与简谐激励的相差, 即受迫振动的初相. 式(2) 表示稳定状态的受迫振动是一个与简谐激励力同频率的简谐振动.f 2(ω2ω2 ) 2( βω) 2即=0 A - A + 2 A= A2 [ (ω2ω2 ) 2β2ω20 - + 4 ]βωA2βωC 2t a nδ===ω2 2 2 20 A -ω Aω0- ωB - D于是得受迫振动的振幅A 和初相δ分别为f 0用旋转矢量法求受迫振动的振幅和初相 A =(ω20- ω2 ) 2 + 4β2ω22βω由式( 2) 得δ= a r ct a nω2 2- ωd2 x= - ω A c o s(ωt - δ)2由此可知, 用旋转矢量法求受迫振动的振幅和初相,比用解微分方程的方法求解直观简单得多, 充分显示了用旋转矢量描述谐振动的优越性其实,任何谐振量都可以用旋转矢量来描述. 因此, 只要用得上旋转矢量法, 就要尽量应用它.d t2= ω2 A c o s[π+ (ωt - δ) ]2βd x = - 2βωA si n(ωt - δ)( 3)d tπ+ (ωt - δ)= 2βωA co s( 4)2参考文献ω20 x =ω0 A c o s(ωt - δ)2 (5)令B =ω2 A 、C = 2βωA 、D = ω2 A 、F = f 0 , 则式(3) 、0 [ 1 ] 赵景员, 王淑贤. 力学[ M ] . 北京: 人民教育出版社, 1979 .470～473赵凯华, 罗蔚茵. 力学[ M ] . 北京: 高等教育出版社, 1995 .273～275张三慧. 波动与光学[ M ]第2 版. 北京: 清华大学出版社,2000 . 24～25马文蔚,解希顺等. 物理学( 下册)[ M ] 第4 版. 北京:高等教育出版社,1999 . 30～31卢德馨. 大学物理学[ M ] . 北京: 高等教育出版社, 1998 .142～143刘克哲. 物理学(上卷) [ M ] 第2 版. 北京: 高等教育出版社,1999 . 155～156周圣源,黄伟民. 高工专物理学[ M ] . 北京: 高等教育出版社,1996 . 61 ,75( 4) 、( 5) 与式( 1) 的右边变为d2 x[ 2 ]= D co s[π+ (ωt - δ) ](6)d t2[ 3 ]π+ (ωt - δ)2βd x = C co s(7)2d t[ 4 ]ω20 x = B c o s(ωt - δ)( 8)(9)f 0 co sωt = F co sωt[ 5 ]将式(6) 、(7) 、(8) 、(9) 代入式(1) ,并用旋转矢量B 、C、D 、F 表示各谐振量, 则有F = B + C + D并且C ⊥B , D ⊥C.旋转矢量图如图2 所示.[ 6 ][ 7 ]。