七年级数学下册53简单的轴对称图形有关轴对称的小故事素材北师大版

与轴对称有关的小故事摘要：1.轴对称的定义和作用2.轴对称在生活中的应用3.轴对称相关的小故事4.轴对称与其他数学概念的关联5.总结与轴对称相关的小故事的意义和启示正文：轴对称是一种基本的数学概念，它在数学、物理、工程等领域有着广泛的应用。

本文将通过一些与轴对称相关的小故事，让大家更深入地了解这一概念，并探讨其在生活中的实际应用。

轴对称的定义是指图形或物体关于某一条直线对称。

这条直线被称为对称轴，对称轴将图形或物体分成两个部分，这两个部分相互镜像。

轴对称在数学中有着重要的地位，它与其他数学概念密切相关，如函数、方程、几何等。

在日常生活中，轴对称也有着广泛的应用。

举个例子，我们可以从一张纸的折叠中看到轴对称的影子。

当我们折叠纸张时，纸的两侧呈现出相同的图案，这就是轴对称的体现。

另外，在建筑、艺术、摄影等领域，轴对称也起着重要作用。

建筑师在设计建筑时，常常会运用轴对称的原理，使建筑更加美观、和谐。

艺术家和摄影师则通过轴对称来营造画面平衡，增强作品的艺术效果。

下面，让我们通过一个小故事来进一步了解轴对称。

故事讲述了一位画家在创作一幅画时，意外发现画中的一棵树与另一棵树在对称轴两侧完全相同。

这使得画家对轴对称产生了浓厚的兴趣，并在今后的创作中，经常运用轴对称的原理。

这个小故事不仅让我们认识到轴对称的魅力，还激发了我们对数学和艺术的兴趣。

轴对称不仅仅是一个数学概念，它还蕴含着深刻的哲学道理。

它教会我们要学会观察生活中的美好，发现事物的内在规律。

同时，轴对称也启示我们要尊重自然、追求和谐。

正如我国古代哲学家老子所说：“道生一，一生二，二生三，三生万物。

万物负阴而抱阳，冲气以为和。

”这里的“和”即为和谐，而轴对称正是这种和谐的数学表现。

总之，与轴对称相关的小故事不仅让我们了解了轴对称的定义和应用，还启发了我们对数学和生活的思考。

关于轴对称的小故事有：
1.有一位老人，他非常喜欢看对称的事物。

有一天，他来到一个
花园里，看到了一朵非常美丽的花，花的形状是一个轴对称图形。

他非常兴奋，于是把花园里的所有花都检查了一遍，发现只有这朵花是轴对称的。

老人非常高兴，把这朵花带回了家，并把它放在了家中最显眼的地方，以便每天都能欣赏到它的美丽。

2.在一个遥远的山村里，有一个叫做阿明的年轻人。

他非常喜欢
画各种各样的图形，尤其是轴对称图形。

每天，他都会爬到村子里的高山上，观察山下的景色，寻找最美的轴对称图形。

他用笔记录下了这些美丽的图形，并把它们画在了纸上。

阿明的画作受到了大家的赞赏，甚至传到了城里。

于是，阿明被邀请到城里，为城市的建筑师们传授他的绘画技巧。

阿明非常高兴，带着自己的绘画作品来到了城里。

他教会了建筑师们如何画出美丽的轴对称图形，并帮助他们在城市中建造了许多美丽的建筑。

北师版七年级下册数学第五章生活中的轴对称轴对称图形轴对称分类轴对称角平分线轴对称实例线段的垂直平分线等腰三角形等边三角形生活中的轴对称轴对称的性质轴对称的性质镜面对称的性质图案设计轴对称的应用镶边与剪纸一、轴对称图形1、如果一个图形沿一条直线折叠后，直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴。

2、理解轴对称图形要抓住以下几点：（1）指一个图形；（2）存在一条直线（对称轴）；（3）图形被直线分成的两部分互相重合；（4）轴对称图形的对称轴有的只有一条，有的则存在多条；（5）线段、角、长方形、正方形、菱形、等腰三角形、圆都是轴对称图形；二、轴对称1、对于两个图形，如果沿一条直线对折后，它们能互相重合，那么称这两个图形成轴对称，这条直线就是对称轴。

可以说成：这两个图形关于某条直线对称。

2、理解轴对称应注意：（1）有两个图形；（2）沿某一条直线对折后能够完全重合；（3）轴对称的两个图形一定是全等形，但两个全等的图形不一定是轴对称图形；1、角平分线所在的直线是该角的对称轴。

2、性质：角平分线上的点到这个角的两边的距离相等。

四、线段的垂直平分线1、垂直于一条线段并且平分这条线段的直线叫做这条线段的垂直平分线，又叫线段的中垂线。

2、性质：线段垂直平分线上的点到这条线段两端点的距离相等。

五、等腰三角形1、有两条边相等的三角形叫做等腰三角形；2、相等的两条边叫做腰；另一边叫做底边；3、两腰的夹角叫做顶角，腰与底边的夹角叫做底角；4、三条边都相等的三角形也是等腰三角形。

5、等腰三角形是轴对称图形，有一条对称轴（等边三角形除外），其底边上的高或顶角的平分线，或底边上的中线所在的直线都是它的对称轴。

6、等腰三角形的三条重要线段不是它的对称轴，它们所在的直线才是等腰三角形的对称轴。

7、等腰三角形底边上的高，底边上的中线，顶角的平分线互相重合，简称为“三线合一”。

8、“三线合一”是等腰三角形所特有的性质，一般三角形不具备这一重要性质。

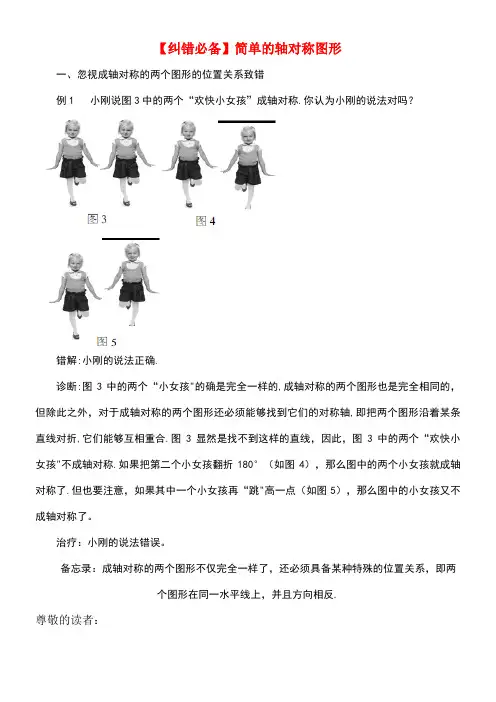
【纠错必备】简单的轴对称图形一、忽视成轴对称的两个图形的位置关系致错例1 小刚说图3中的两个“欢快小女孩”成轴对称.你认为小刚的说法对吗？错解:小刚的说法正确.诊断:图3中的两个“小女孩"的确是完全一样的,成轴对称的两个图形也是完全相同的，但除此之外，对于成轴对称的两个图形还必须能够找到它们的对称轴,即把两个图形沿着某条直线对折,它们能够互相重合.图3显然是找不到这样的直线，因此，图3中的两个“欢快小女孩"不成轴对称.如果把第二个小女孩翻折180°（如图4），那么图中的两个小女孩就成轴对称了.但也要注意，如果其中一个小女孩再“跳"高一点（如图5），那么图中的小女孩又不成轴对称了。

治疗：小刚的说法错误。

备忘录：成轴对称的两个图形不仅完全一样了，还必须具备某种特殊的位置关系，即两个图形在同一水平线上，并且方向相反.尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

有关轴对称的小故事对称性在自然界中的存在是一个普遍的现象。

99％的现代动物是左右对称祖先的后代。

连海葵这种非左右对称动物的后代，也存在对称性；对称性甚至在左右对称和非左右对称动物分化之前就已具有……在植物界，我们有多少次惊异于那些具有完美对称性蕨类、铁树的叶子和娇艳的花朵？生命里如果没有对称性会是什么样子呢？如果动物只两条腿，要么象人一样令人畏惧；要么不能生存。

如果人不是左右对称，只有一只眼睛、一只耳朵和半个脸……世界就不再美好了。

人具有独一无二的对称美，所以人们又往往以是否符合“对称性”去审视大自然，并且创造了许许多多的具有“对称性”美的艺术品：服饰、雕塑和建筑物。

对称性对于人，不仅仅是外在的美，也是健康和生存的需要。

如果只有一只眼睛，人的视野不仅变小、对与目标的距离判断不精确，而且对物体的立体形状的认知会发生扭曲。

如果一只耳朵失聪，对于声源的定位就会不准确：因为当人对声源定位时，大脑需要声音对于听者的方位仰角线索，也需要到达左右耳间的时间和强度差线索。

对于野外生存的动物，失去声源定位的能力，意味着生命随时会受到威胁。

左右手脚需要默契的配合。

对于花朵，如果花冠的发育失去对称性，雄蕊就会失去受粉能力，不能传种接代，物种将绝灭。

生命从最原始的单细胞动物向多细胞后生动物演化，最早拥有了以“对称性”为特征的复杂性：例如从单倍体生物到二倍体生物。

二倍体生物都能进行两性繁殖，有雌有雄；每个个体都有来自于父母的染色体和相应的基因，虽然隐性基因并不表现出来。

在越来越多基因被克隆出来以后，寻找控制对称性状的基因，成为寻找新发现的有力线索。

一般相信，某些对称性状是有若干对基因所控制的，也决定某些非对称性状的特化。

在科学研究中，对称性给科学家们提供了无限想象的空间，也是揭示新发现和否定错误观念的手段。

生命科学家不止探讨认识生命活动的本质，而且也探讨存在于生命中的美、为什么这么美？人大脑的两个半球，从它们的沟回和细胞排列层次看，非常相似，具有完美的对称性；这种对称性之于两手、两脚的对称性无异，似乎功能应是一样的。

初中尺规作图数学史尺规作图是起源于古希腊的数学课题.只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题.平面几何作图，限制只能用直尺、圆规.在历史上最先明确提出尺规限制的是伊诺皮迪斯.他发现以下作图法：在已知直线的已知点上作一角与已知角相等.这件事的重要性并不在于这个角的实际作出，而是在尺规的限制下从理论上去解决这个问题.在这以前，许多作图题是不限工具的.伊诺皮迪斯以后，尺规的限制逐渐成为一种公约，最后总结在《几何原本》之中.初等平面几何研究的对象，仅限于直线、圆以及由它们（或一部分）所组成的图形，因此作图的工具，习惯上使用没有刻度的直尺和圆规两种.限用直尺和圆规来完成的作图方法，叫做尺规作图法.最简单的尺规作图有如下三条：⑴ 经过两已知点可以画一条直线；⑵ 已知圆心和半径可以作一圆；⑶ 两已知直线；一已知直线和一已知圆；或两已知圆，如果相交，可以求出交点；以上三条，叫做作图公法.用直尺可以画出第一条公法所说的直线；用圆规可以作出第二条公法所说的圆；用直尺和圆规可以求得第三条公法所说的交点.一个作图题，不管多么复杂，如果能反复应用上述三条作图公法，经过有限的次数，作出适合条件的图形，这样的作图题就叫做尺规作图可能问题；否则，就称为尺规作图不能问题.历史上，最著名的尺规作图不能问题是：⑴ 三等分角问题：三等分一个任意角；⑵ 倍立方问题：作一个立方体，使它的体积是已知立方体的体积的两倍；⑶ 化圆为方问题：作一个正方形，使它的面积等于已知圆的面积.这三个问题后被称为“几何作图三大问题”.直至1837年，万芝尔（Pierre Laurent Wantzel）首先证明三等分角问题和立方倍积问题属尺规作图不能问题；1882年，德国数学家林德曼（Ferdinand Lindemann）证明π是一个超越数（即π是一个不满足任何整系数代数方程的实数），由此即可推得根号π(即当圆半径1r 时所求正方形的边长）不可能用尺规作出，从而也就证明了化圆为方问题是一个尺规作图不能问题.若干著名的尺规作图已知是不可能的，而当中很多不可能证明是利用了由19世纪出现的伽罗华理论.尽管如此，仍有很多业余爱好者尝试这些不可能的题目，当中以化圆为方及三等分任意角最受注意.数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书.还有另外两个著名问题：⑴ 正多边形作法·只使用直尺和圆规，作正五边形.·只使用直尺和圆规，作正六边形.·只使用直尺和圆规，作正七边形——这个看上去非常简单的题目，曾经使许多著名数学家都束手无策，因为正七边形是不能由尺规作出的.·只使用直尺和圆规，作正九边形，此图也不能作出来，因为单用直尺和圆规，是不足以把一个角分成三等份的.·问题的解决：高斯，大学二年级时得出正十七边形的尺规作图法，并给出了可用尺规作图的正多边形的条件：尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积，解决了两千年来悬而未决的难题.⑵ 四等分圆周只准许使用圆规，将一个已知圆心的圆周4等分．这个问题传言是拿破仑·波拿巴出的，向全法国数学家的挑战.尺规作图的相关延伸：用生锈圆规(即半径固定的圆规)作图1.只用直尺及生锈圆规作正五边形2.生锈圆规作图，已知两点A、B，找出一点C使得AB BC CA==.3.已知两点A、B，只用半径固定的圆规，求作C使C是线段AB的中点.4.尺规作图，是古希腊人按“尽可能简单”这个思想出发的，能更简洁的表达吗？顺着这思路就有了更简洁的表达.10世纪时，有数学家提出用直尺和半径固定的圆规作图. 1672年，有人证明：如果把“作直线”解释为“作出直线上的2点”，那么凡是尺规能作的，单用圆规也能作出！从已知点作出新点的几种情况：两弧交点、直线与弧交点、两直线交点，在已有一个圆的情况下，那么凡是尺规能作的，单用直尺也能作出！.五种基本作图：初中数学的五种基本尺规作图为：1.做一线段等于已知线段2.做一角等于已知角3.做一角的角平分线4.过一点做一已知线段的垂线5.做一线段的中垂线下面介绍几种常见的尺规作图方法：⑴ 轨迹交点法：解作图题的一种常见方法.解作图题常归结到确定某一个点的位置.如果这两个点的位置是由两个条件确定的，先放弃其中一个条件，那么这个点的位置就不确定而形成一个轨迹；若改变放弃另一个条件，这个点就在另一条轨迹上，故此点便是两个轨迹的交点.这个利用轨迹的交点来解作图题的方法称为轨迹交点法，或称交轨法、轨迹交截法、轨迹法.【例1】 电信部门要修建一座电视信号发射塔，如下图，按照设计要求，发射塔到两个城镇A 、B 的距离必须相等，到两条高速公路m 、n 的距离也必须相等，发射塔P 应修建在什么位置？m【分析】 这是一道实际应用题，关键是转化成数学问题，根据题意知道，点P 应满足两个条件，一是在线段AB 的垂直平分线上；二是在两条公路夹角的平分线上，所以点P 应是它们的交点.【解析】 ⑴ 作两条公路夹角的平分线OD 或OE ；⑵ 作线段AB 的垂直平分线FG ；则射线OD ，OE 与直线FG 的交点1C ，2C 就是发射塔的位置.⑵ 代数作图法：解作图题时，往往首先归纳为求出某一线段长，而这线段长的表达式能用代数方法求出，然后根据线段长的表达式设计作图步骤.用这种方法作图称为代数作图法.【例2】 只用圆规，不许用直尺，四等分圆周（已知圆心）.【分析】 设半径为1..我们的任务就是做出这个长度..设法构造斜边1.【解析】 具体做法：⑴ 随便画一个圆.设半径为1.⑵ 先六等分圆周.⑶ 以这个距离为半径，分别以两个相对的等分点为圆心，同向作弧，交于一点.（“两个相对的等分点”其实就是直径的两端点啦！两弧交点与“两个相对的等分点”形成的是一个底为2.可算出顶点距圆心距离）的长度等分圆周就可以啦！⑶ 旋转法作图：有些作图题，需要将某些几何元素或图形绕某一定点旋转适当角度，以使已知图形与所求图形发生联系，从而发现作图途径.【例3】 已知：直线a 、b 、c ，且a b c ∥∥.求作：正ABC ∆，使得A 、B 、C 三点分别在直线a 、b 、c 上.c b aD'DC B Acb a【分析】 假设ABC ∆是正三角形，且顶点A 、B 、C 三点分别在直线a 、b 、c 上.作AD b⊥于D ，将ABD ∆绕A 点逆时针旋转60︒后，置于'ACD ∆的位置，此时点'D 的位置可以确定.从而点C 也可以确定.再作60BAC ∠=︒，B 点又可以确定，故符合条件的正三角形可以作出.【解析】 作法：⑴ 在直线a 上取一点A ，过A 作AD b ⊥于点D ；⑵ 以AD 为一边作正三角形'ADD ；⑶ 过'D 作''D C AD ⊥，交直线c 于C ；⑷ 以A 为圆心，AC 为半径作弧，交b 于B (使B 与'D 在AC 异侧).⑸ 连接AB 、AC 、BC 得ABC ∆.ABC ∆即为所求.⑷ 位似法作图：利用位似变换作图，要作出满足某些条件的图形，可以先放弃一两个条件，作出与其位似的图形，然后利用位似变换，将这个与其位似得图形放大或缩小，以满足全部条件，从而作出满足全部的条件.【例4】 已知：一锐角ABC ∆.求作:一正方形DEFG ，使得D 、E 在BC 边上，F 在AC 边上，G 在AB 边上.C B AG'F'E'D'GF E D C B A【分析】 先放弃一个顶点F 在AC 边上的条件，作出与正方形DEFG 位似的正方形''''D E F G ，然后利用位似变换将正方形''''D E F G 放大（或缩小）得到满足全部条件的正方形DEFG .【解析】 作法：⑴ 在AB 边上任取一点'G ，过'G 作''G D BC ⊥于'D⑵ 以''G D 为一边作正方形''''D E F G ，且使'E 在'BD 的延长线上.⑶ 作直线'BF 交AC 于F .⑷ 过F 分别作''FG F G ∥交AB 于G ；作''FE F E ∥交BC 于E .⑸ 过G 作''GD G D ∥交BC 于D .则四边形DEFG 即为所求.⑸ 面积割补法作图：对于等积变形的作图题，通常在给定图形或某一确定图形上割下一个三角形，再借助平行线补上一个等底等高的另一个三角形，使面积不变，从而完成所作图形.【例5】 如图，过ABC ∆的底边BC 上一定点，P ，求作一直线l ，使其平分ABC ∆的面积.【分析】 因为中线AM 平分ABC ∆的面积，所以首先作中线AM ，假设PQ 平分ABC ∆的面积，在A M C ∆中先割去AMP ∆，再补上ANP ∆.只要NM AP ∥，则A M P ∆和AMP ∆就同底等高，此时它们的面积就相等了.所以PN 就平分了ABC ∆的面积.【解析】 作法：⑴ 取BC 中点M ，连接,AM AP ;⑵ 过M 作MN AP ∥交AB 于N ；⑶ 过P 、N 作直线l .直线l 即为所求. NM P CB Al。

学必求其心得，业必贵于专精
《利用轴对称进行设计》
一、阅读资料
《艺术作品中的对称》
许多著名画家在作品中运用简单的图形创造出了奇妙的韵意。

法国著名画家V·瓦萨雷利于1969年创作出了名画《委加·派尔》，画中仅仅用了圆形图案，就形成了一幅动态的轴对称图形!
在从古至今的艺术创作中,不仅画家大量运用了对称，许多别的艺术家也经常运用对称的手法。

如雕刻家威廉斯多佛1971年在加蓬《非洲人的设计》中创作的“木制卫兵雕像”就是典型的雕刻艺术中的对称。

二、拓展练习
练习1:分别以虚线为对称轴画出下列各图的另一半，并说明完成后的图形可能代表什么含义.
交通标识
L形图案，请你再添加一个小正方形使它们能组成一个轴对称图形.（给出三种不同的作法）。