当前位置：文档之家 › 6-湍流预混火焰讲解

6-湍流预混火焰讲解

  • 格式：ppt
  • 大小：2.23 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

6-层流预混火焰传播与稳定

6-层流预混火焰传播与稳定
9
RR 9.55 *10 * (0.1997)
5
1.75
0.0301 0.1 0.1095 1.65 *( ) *( ) * 44 44 32
107.3kg /(s m 3 )
热扩散系数为
a
(T ) u c p (T )
在计算时应注意到平均温度针对于整个火焰厚度而言，这是因为 热传导不仅发生在反应区，而且在预热区也是存在的，故
化学参数的影响
（1）混合比（混气成分）的影响
层流火焰传播速度随燃料-氧化剂配比而变化， 主要是由于温度随混合比的变化所引起。对碳氢化 合物燃料，在化学恰当比或者燃料稍富的混气中， 火焰传播速度达到最大。
一般认为火焰温度最高的混合物火焰速度也最大， 在很贫或者很富的燃气中，由于燃料或者氧化剂太 少，反应生成热太少，而实际燃烧设备不可能绝热， 固难以维持火焰传播必需的热量积累，火焰在其中 不能传播。 火焰传播有浓度的上下限
变化
假设燃气中没有氧气或者燃料，可以得出氧气和燃料的平均质量 分数分别为：
w f 0.5( w f ,u 0) 0.06015* 0.5 0.0301 wo2 0.5[0.2331* (1 w f ,u ) 0] 0.1095
其中0.2331为空气中氧的质量分数，化学恰当比的丙烷-空气混合 物空燃比A/F=15.625 而化学反应速率为：


Tu 350K ; Tu , ref 298K ; Pref 1atm S L, ref BM B2 ( M )
2
指数γ、β为当量比ф的函数，表示为： γ= 2.18-0.8（ ф -1） β= -0.16+0.22（ ф -1）
惰性物质或添加剂的影响：

第六讲 预混合气体火焰-1

第六讲 预混合气体火焰-1

f
f
即为Hugoniot曲线上任意点的切线斜率。
（3）Raleigh-Hugoniot方程
• 火焰锋面后方的熵变：
∵
dq du pdV
T f dS f de f Pf dV
dS f Ps Pf 1 1 1 dPf Tf ( ) 1 1 1 1 d ( ) 2 s f d f s f f
• 或将u f 代入式（2）
f ( Ps Pf ) u s ( s f )
2 s
s2us2
s f ( Ps Pf ) ( s f )
6.1.2 爆燃与缓燃-基本方程
• 同理： •
Ps Pf u u 1 1 f s
2 2 s s 2 2 f f
过点S的直线（且 C <0）在第一、三象限不复存在。 凡满足瑞利方程的均为过点S的直线簇。
C 0 ， s Pf ，等压线， P
m 0 。
等密线，m 。
（ C ，Pf
s f ），
（2）Hugoniot（雨果尼特）方程
将式（1）与能量方程耦合
递的热量，提高自身温度，火焰逐渐向未燃区传播。 燃烧前后反应物浓度、温度变化情况见上图示意。 描述燃烧波中这些量得变化称为火焰结构。 预混火焰可以是固定的，也可以是以一定速度传播 的。
6.1.2 爆燃与缓燃
• 一根很长的等截面水平管内充满可燃混气，在左端 点燃，燃烧波将以某恒定的速度向右传播。
6.1.2 爆燃与缓燃
s f
( Ps
C
s
)
C
f
(4)
• 瑞利方程另一种形式。

湍流燃烧火焰面模式理论及应用(孙明波,白雪松,王振国著)PPT模板

湍流燃烧火焰面模式理论及应用(孙明波,白雪松,王振国著)PPT模板

0 5
2.5湍流预混 燃烧算例验证
0 6
2.6带自点火 特性的预混火 焰传播模型
第2章湍流预混燃 烧
参考文献
第2章湍流预混燃烧
2.1层流预混火焰
2.1.1层流 预混火焰结 构
2.1.2层流 预混火焰温 度
第2章湍流预混燃烧
2.2湍流预混火焰
0 1 2.2.1湍流预混火焰的基本性质
02
2.2.2湍流脉动与火焰的相互作 用
第1章湍流燃烧及其数值模拟概述
1.1湍流燃烧基本特性
1.1.1湍流 的基本特 性
1.1.2湍流 燃烧的特 点
第1章湍流燃烧及 其数值模拟概述
1.2化学反应流的数学描 述
1
1.2.1化学反应流控制方程
2
1.2.2化学反应机理及反应速率
第1章湍流燃烧及 其数值模拟概述
1.3湍流燃烧模拟的一般方 法
2.4.4G方程 和C方程比较
第2章湍流预混燃烧
2.5湍流预混燃烧算例验证
1
2.5.1均匀各向同性湍流中的火 焰核增长
2
2.5.2三角棱柱火焰稳定器的燃 烧模拟
3
2.5.3低旋流燃烧器的火焰稳定
4
2.5.4本生灯的火焰形状
第2章湍流预混燃烧
2.6带自点火特性的预混火焰传播模型
2.6.1预混 火焰自点火 耦合模型
n解和化学 平衡解
04
03
3.2.4火焰面结构的 渐近解
3.2.3详细化学反应 机理对层流扩散火 焰的影响
第3章扩散燃烧
3.3湍流扩散燃烧火焰面模型
01 3 .3 .1 扩散火焰 面模 02 3 .3 .2 火焰面模 型方
型合理性验证

湍流预混火焰模型概要

湍流预混火焰模型概要
R fu ,T (m fu m fu ,b ) S / u

(3-56)


流场较均匀的区域，合理地估算层流火焰传播速度是 正确运用拉切滑模型的关键之一 。 层流火焰传播速度是可燃气的物理化学性质，它取决 于混合物的热力学状态(如压力和温度)，对温度尤为 敏感。 丙烷和空气当量比混合物的火焰传播速度 S 0.113(T / 298)2 0.186(T / 298) 0.02 (m/s) (3-57) 求S的问题转化为求T。

反应度τ的脉动均方值 gτ

定义
g 2 ( ) 2 (m fu m fu ) 2 /(m fu ,b m fu ,u ) 2 m /(m fu ,b m fu ,u )
2 fu 2
(3-60)

2 gτ和 mfu 应当遵守同一类型的微分方程。
反应度τ的平均值和脉动均方值 gτ的确定
对比用k - ε模型和混合长度模型计算湍流粘度 t C k 1/ 2 C CD k 2 / 的公式 2) 假定 k 1/ 2正比于混合长度与均流速度梯度绝对 值的乘积 则ε/k正比于均流速度梯度的绝对值 3) 燃烧速率一定与燃料浓度有关 二维边界层问题湍流燃烧速率 u (3-42) R c m

5 平面管道内火焰稳定器后面的燃烧场

Spalding et al 结果优于只用 阿伦纽斯类型 的公式(3-48)得 到的结果，与 实验数据的趋 势符合
6 对旋涡破碎模型的评价
功绩在于正确地突出了流动因素对燃烧速率的 控制作用，给出了简单的计算公式，为湍流燃 烧过程的数学模拟开辟了道路。 不足：该模型未能考虑分子输运和化学动力学 因素的作用 适用范围：一股说来，EBU模型只适用于高雷 诺数的湍流预混燃烧过程。

第六讲 预混可燃气的湍流燃烧 PPT课件

第六讲 预混可燃气的湍流燃烧 PPT课件
第六讲 预混可燃气的湍流燃烧
§6.1 湍流燃烧及其特点
实际各种燃烧装置中的燃烧过程往往都是湍流燃烧过程。
所谓湍流的确切定义尚难明确，但与层流的平滑分布和有 秩序流动相比较，可认为它具有：
(1) 不规则性 只能用统计方法 (2) 扩散性 传递速度加快 (3) 具有明显的旋涡脉动 （尺寸大小：含能大、小， 脉动具有耗散性） (4) 是一种流动（是流体受约束转弱的自收运动状态 ）
l
大尺度湍流火焰
l
强湍流火焰 湍流的脉动速度远大于层流火焰传播速度，此 时有：
u' SL
弱湍流火焰 湍流的脉动速度小于层流火焰传播速度，此时有
u' SL
湍流火焰稳定燃烧的条件： 一维湍流能量方程：
CP ST
dT dx

d dx
[(

T
)
dT dx
]

sQs
为便于分析，取无量纲后：
§6.2 湍流燃烧火焰传播速度
湍流燃烧火焰传播速度:
湍流火焰前沿法向相对于新解可燃气运动的速 度
ST=u COSθ
测定ST的常用方法有二种。 (1) 定常开口火焰，本生灯法
(2) 定常封闭火焰
对于定常开口火焰，ST的大小测定
V
(1) 测得U及θ
F
(2) 流入可燃预混气流量除以湍流火焰表面积
如何确定F是很困难的。
层流火焰与湍流火焰的特点比较
当Re < 2300 层燃火焰 a) 前沿厚度0.01~0.1mm高度； b)火焰前沿光滑基本成正圆锥形； c) 20~200cm/s
当Re>2300时，湍流火焰（渐变过程） a) 火焰高度很小。说明 ST>>Sl b) 火焰前沿出现脉动和弯曲 c) 收光区模糊 d) 有明显的噪音 e) 有较宽的反应区域

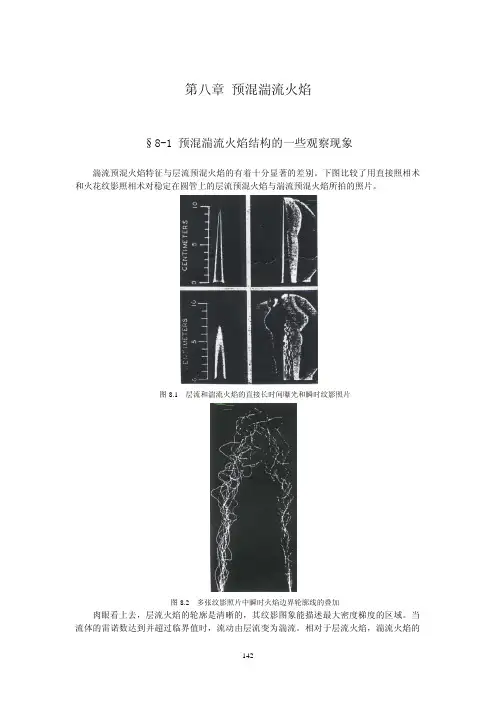
第八章 预混湍流火焰

第八章 预混湍流火焰
在这种方法中用激光片来照射流动区域火焰前锋位于亮和暗的分界线上亮的地方是激光片被粒子散射的结果而暗的地方则是由于燃烧放热气体膨胀从而使粒子的密度减小减少了对激光的散射所致
第八章 预混湍流火焰
§8-1 预混湍流火焰结构的一些观察现象
湍流预混火焰特征与层流预混火焰的有着十分显著的差别。下图比较了用直接照相术 和火花纹影照相术对稳定在圆管上的层流预混火焰与湍流预混火焰所拍的照片。
lmax ＝ l ＝最大旋涡尺寸＝积分尺寸
lmin ＝ l ຫໍສະໝຸດ 最小旋涡尺寸＝Kolmogorov 尺度
于是有： lmax / lmin = l /η = C Rel 3 / 4
因此，在这个例子里， ST / S L = (C Rel 3/ 4 ) D−2 为了使 D 的低值和高值与实验结果相一致，我们注意到，对 D = 2 (亦即低湍流强
D = 2 + (2 + μ) / 6
其中， μ = 0.25 ~ 0.50 ，所以， D = 2.375 ~ 2.417
由实验得，D 取决于 u ' ，其变化范围是 D 由 2（ u ' / S L << 1 ）变化到 2.35（ u ' / S L >> 1 ）。
下面，我们必须选择 lmax 和 lmin ，我们设
（8-1）
∫ P( f )( f − f )2 df
σ 2(X) ≡
∫ P( f )df
= ∫ P( f )( f
−
f ) 2 df
（8-2）
方差的平方根 σ 2 是常用的标准差，或者是 f 的均方根值。f 的均方根值与平均值的比值
定义脉动度，或为湍流强度 I f
If

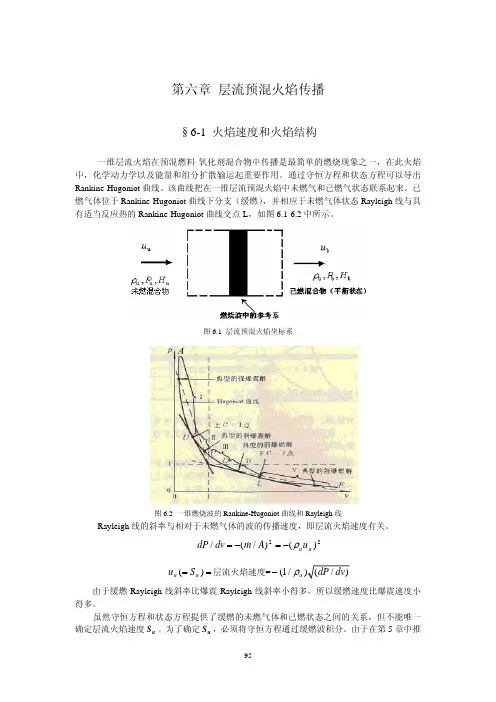
第六章 预混层流火焰

第六章 预混层流火焰

第六章 层流预混火焰传播§6-1 火焰速度和火焰结构一维层流火焰在预混燃料-氧化剂混合物中传播是最简单的燃烧现象之一，在此火焰中，化学动力学以及能量和组分扩散输运起重要作用。

通过守恒方程和状态方程可以导出Rankine-Hugoniot 曲线。

该曲线把在一维层流预混火焰中未燃气和已燃气状态联系起来。

已燃气体位于Rankine-Hugoniot 曲线下分支（缓燃），并相应于未燃气体状态Rayleigh 线与具有适当反应热的Rankine-Hugoniot 曲线交点L ，如图6.1-6.2中所示。

图6.1 层流预混火焰坐标系图6.2 一维燃烧波的Rankine-Hugoniot 曲线和Rayleigh 线Rayleigh 线的斜率与相对于未燃气体的波的传播速度，即层流火焰速度有关。

22)()/(/u u u A mdv dP ρ−=−=& ==)(u u S u 层流火焰速度=)/()/1(dv dP u ρ−由于缓燃Rayleigh 线斜率比爆震Rayleigh 线斜率小得多，所以缓燃速度比爆震速度小得多。

虽然守恒方程和状态方程提供了缓燃的未燃气体和已燃状态之间的关系，但不能唯一确定层流火焰速度u S 。

为了确定u S ，必须将守恒方程通过缓燃波积分。

由于在第5章中推导的方程是非线性耦合微分方程，其准确解只有通过数值积分才能获得。

它需要很大的计算资源。

为了考察层流火焰的某些特征（如火焰速度和厚度）以及这些特征与燃烧参数如燃料类型、化学配比、压力及未燃气体的温度的关系，对方程组进行了简化，以便能分析求解。

要得到简化的模型，需要引入一系列的假设。

我们从考察参考系建立在火焰上的层流火焰结构的某些方面入手。

如前所述，这些计算是针对等压过程进行的。

但是对一维缓燃的Rankine-Hugoniot 曲线，如图6.2所示，已燃气的压力小于未燃气的压力。

现在我们需要考察压力减少的数值是否小到可以忽略的程度。

燃烧学-预溷合气燃烧及火焰传播

燃烧学-预溷合气燃烧及火焰传播

4.1 层流火焰传播 (laminar flame）
预混可燃气体流速不高（层流状态）时 的火焰传播称为层流火焰传播。
一、层流火焰结构与传播机理
层流火焰图
层流火焰前沿浓度和温度变化
火焰结构特点
火焰前沿厚度很薄，一般不超过1mm，只有十分之几 毫米甚至百分之几毫米厚。
层流火焰图
前沿的厚度很小，但温度和浓度的变化很大，因而在 火焰前沿中出现了极大的浓度梯度及温度梯度。这就 引起了火焰中强烈的扩散流和热流。
us us
Sl＝u0
(u p、us反方向） (u p、us同方向）
对固定火焰，火焰面静止不动，即up=0，则Sl = u0 = us
即：火焰传播速度就等于未燃混合气进入火焰面的流速，
两者大小相等方向相反。
可燃气体和空气混合物在20℃及760厘米水银柱 下的火焰前沿移动的正常速度值
可燃气体
H2 CO CH4 C2H2 C2H4
在火焰前沿厚度的很大一部分上，化学反应的速度很
小，称为预热区，以 δp 表示。而化学反应主要集中 在很窄的区域 δc 中进行，称其为化学反应区。
火焰前沿传播机理
火焰传播的热理论 认为火焰中反应区(即火焰前沿)在空间的移动，取
决于反应区放热从而向新鲜混合气的热传导。
火焰传播的扩散理论 认为凡是燃烧都属于链式反应，在链式反应中借助
燃烧放热率比层流火焰的 大的多。
湍流火焰与层流火焰的区别
湍流火焰传播速度的定义——St
湍流火焰传播速度指湍流火焰前沿 任一处法向相对于未燃混合气运动的速 度。
二、湍流特性
湍流的基本特性：湍流中充满大小不等、高速旋转的流体微 团，或称涡团，在不断地做无规则的运动，使流体各点每瞬 时的速度、压力都在做随机的变化。

燃烧学讲义-第6章气体燃料的燃烧

燃烧学讲义-第6章气体燃料的燃烧

w'
uce
ut A = 1+ t uce a
ut a+ A a t … … uce ∝ … … = ∴ uce a τrj
At：湍动输运所引起的折算热扩散率
A t a时，有 ut = uce
A t （一般情况下 A t a
当
a）
A ut t ∝ Re = Re 若流体为管内流动， 若流体为管内流动，一般认为 uce a
uce
ut uce
18
一、湍流传播的理论 一、湍流传播的理论
表面燃烧理论（舍谢尔金）
火焰面是层流型的， 火焰面是层流型的 ， 湍流脉动在一定空间内使燃烧 面弯曲、皱折，乃至破裂， 小岛”状的封闭小块， 面弯曲、 皱折 ，乃至破裂， 成“小岛”状的封闭小块， 这样增大了燃烧面积，从而增大了燃烧速度。 这样增大了燃烧面积，从而增大了燃烧速度。
2Qwm RT 2 a 2Q a lr uce = wmdT = ∴ T −T0 λ ∫ ρCp (Tlr −T0 )2 E lr B
10
燃尽时间：τrj =
ρCp (Tlr −T0 )
wmQ
uce ∝
a
τrj
火焰锋面厚度δ及可燃混合物升温预热区厚度 火焰锋面厚度 及可燃混合物升温预热区厚度S
RT 2 S定义为 T = Tlr − lr 点做 T = 定义为在 定义为 E
2
火焰传播的形式
缓燃（ 正常传播） 缓燃 （ 正常传播 ） ：火焰锋面以导热和 对流的方式传热给可燃混合物引起的火 焰传播， 也可能有辐射（ 煤粉） 焰传播 ， 也可能有辐射 （ 煤粉 ） 。 传播 速度较低（ 速度较低（1~3m/s），传播过程稳定。 m/s） 传播过程稳定。 爆燃：绝热压缩引起的火焰传播 ， 爆燃 ：绝热压缩引起的火焰传播， 是依 靠激波的压缩作用使未燃混合气的温度 升高而引起化学反应， 升高而引起化学反应 ， 从而使燃烧波不 断向未燃气推进，传播速度大于 1000m/s。 1000m/s。

第六部分预混可燃气的火焰

第六部分预混可燃气的火焰

Q0W0dT
右图是释热速度与温度的关系，可见：
Ti
T0
Q0W0
dT

Tf Ti
Q0W0 dT
因此可以认为：
Tf
Ti
Q0W0 dT

Tf T0
Q0W0 dT

Q0W0
平均 T f
T0
U

1
cp Ti
T0
2 Q0W0 平均 Tf T0
2019/5/24
3、火焰前锋很薄，但是理论分析时不能忽略。锋面内温度、浓度梯度很大， 存在自然对流、强制对流、导热等热量交换形式以及流动、扩散等质量交 换形式。存在强烈光辐射，可以根据发光区判断反应区位置。
2019/5/24
河北工业大学能源与环境学院
8
一维层流平面火焰锋面内能量方程的建立
对于火焰锋面内厚度为
Δx的微元，温度T沿可燃物
如图，设火焰前锋某点法向速度为Up，该 点可燃物流速为w，则火焰传播速度为：
U=Up+w
1、静止气流中，w=0，U=Up，即 火焰传播速度等于锋面法向速度；
2、当火焰锋面静止时，Up=0， 火焰传播速度等于气流速度；
3、对于理想化一维平面火焰， 火焰锋面速度处处相等。
2019/5/24
河北工业大学能源与环境学院
猝熄效应：由于管壁的散热，火焰在壁面附近受到冷却，温度降低 而熄灭，即在管壁附近不存在火焰。从管壁开始，无火焰存在的那 段径向距离称为猝熄距离。
火焰锋面的厚度一般在0.01~1mm之间，相对与系统的 特性尺寸来说很小，因此理论分析时将之看作平面。
2019/5/24
河北工业大学能源与环境学院
4

燃烧理论6火焰传播与稳定解析

燃烧理论6火焰传播与稳定解析

dx
Tf
层流火焰传播速度推导
能量方程 边界条件
预热区：
0ul C p
dT dx
d (dT ) dx dx
x
, T
T0 ,
dT dx
0
反应区：
d 2T dx 2
WQ
0
x 0, T Tf
x
, T
Tm ,
dT dx
0
dT 0ulCp (Tf T0 )
dx
＝
dT 2 TmWQdT
实际上，只有极少数的火焰传播过程是单纯受热力理论控制或 单纯是受扩散理论控制的，碳氢化合物燃烧时热力理论和扩散理论 同时起作用。在一般情况下热力理论比较接近于实际，被认为是目 前比较完善的火焰传播理论。
四、层流火焰的内部结构及其传播机理
设：u0 = ul，则火焰锋 面驻定。 将火焰锋面可分为两部 分：
三、层流火焰速度(Laminar flame speed, SL）
层流火焰传播的速度定义为流动状态为层流时的火 焰锋面在其法线方向相对于新鲜混合气的传播速度。
层流火焰速度：SL(标量) 火焰传播速度：S (矢量)
流场速度：U(矢量)
相对于未燃预混气体的层 流火焰速度：
Su = Uu− dxf / dt = SL
热力理论：火焰中化学反应主要是由于热量的导入使分子热 活化而引起的，所以火焰前沿的反应区在空间中的移动决定于从 反应区向新鲜预混可燃气体传热的传导率。并不否认火焰中心有 活性中兴存在和扩散，但认为在一般的燃烧过程中活化中心的扩 散对化学反应速度的影响不是主要的。
扩散理论：火焰中化学反应主要是活化中心（如H、OH 等）向新鲜预混可燃气体扩散，促进使其链锁反应发展所致。

6-湍流预混火焰讲解

6-湍流预混火焰讲解
现象： 火焰锋面扭曲皱折 火焰锋面未被吹破，仍然是连续的
大尺度弱湍流传播速度确定——小 火焰模型（表面理论）
设薄层焰锋的传播速度仍然是un，那么单位时间内焰锋锋 面烧掉的混合气是Acun，它应与湍流火焰传播速度ut和湍 流焰锋的平均面积Ap的乘积相等，即：
Acun=Aput 或 ut=Acun/Ap 因为Ac>Ap,故ut>un, 若把湍流气团设想成凹凸不平的很多 小的焰锋，则ut>un, 等于这些小的椎体表面积和底面积之 比。 ——小火焰模型，亦称湍流火焰传播的表面理论
燃烧学
6-湍流预混火焰
湍流预混火焰传播 湍流预混火焰传播图域 湍流预混火焰传播速度确定 湍流火焰传播速度影响因素
第一节 湍流预混火焰传播
研究湍流火焰的目的
（1）工程中的燃烧装置多为湍流燃烧 （2）确定湍流特性对火焰传播的影响 雷诺数Re=ρvL/μ 直管段中： Re<2300时，层流； Re>3200时，湍流 此时火焰为湍流火焰
（5）混气浓度 化学恰当比或偏富时速度最大
St
m
Au
湍流预混火焰传播速度要比层流预混火焰传 播速度快
湍流火焰比层流火焰传播快的原因
（1）湍流流动使火焰变形，火焰表面积增加，因而增大了 反应区； （2）湍流加速了热量和活性中间产物的传输，使反应速率 增加，即燃烧速率增加； （3）湍流加快了新鲜混合气和燃气之间的混合，缩短了混 合时间，提高了燃烧速度。 湍流火焰理论基于上述概念发展起来的。 湍流火焰传播理论主要有两种： （1）表面褶皱理论（邓克尔和谢尔金） （2）容积燃烧理论（萨默菲尔德和谢京科夫）
第二节 湍流预混火焰传播图域
湍流预混火焰的性质既依赖于预混层流火焰的特性（如SL和

第六章 预混合气的紊流燃烧ppt课件

第六章 预混合气的紊流燃烧ppt课件
第六章 预混合气的紊流燃烧
第六章 预混合气的紊流燃烧
• 流体运动有层流和紊流之分 • 紊流状态将使火焰传播速度大大加快 • 紊流火焰的特点之一是火焰面有许多皱折
• 绝大多数燃烧设备中的火焰都是紊流火焰，紊流火 焰可使燃烧设备的单位空间的放热率大大提高。
3
汽油机
燃气轮机
工业气体燃烧器
燃油加热器
紊流模型
• 由于动量方程中出现了新的紊流应力项，因此第三 章中的封闭方程组就变的不封闭了，为了使方程组 封闭，常常根据经验建立一些补充的，用代数方程 或微分方程表示的关系式，作为约束条件，即所谓 的“紊流模型” • 比较简单，应用最早并且最广泛的模型：普朗特混 合长模型 • 假设紊流应力与平均流动参数的关系和分子粘性应 力与流动参数的关系相同
u u j i u u T i j T x x i j
• 则6-9右侧方括号中的项变为 • 普朗特参照分子运动论，假设
uj u i T x x i j 2 l u T m
u u u ( y ) u ( y l ) l 1 m m y
• 同样，由y+lm层进入y层时，也将引起一个脉动
• 因此假设
u u u ( y ) u ( y l ) l 2 m m y 2 u u 2 u lm ，带入6-12，得 T lm y y
A BA B 两个时均值的乘积的时均值等于两个时均值的乘积
A B A B 0
பைடு நூலகம்
• 由以上各关系式得
BB AB A A A B A B AB AB
B AB A B 0 • 若A、B各自独立，不互相关联，则 A

第三节-扩散火焰与预混火焰讲解学习

第三节-扩散火焰与预混火焰讲解学习
(1)减小喷口直径，增加喷嘴数量。利用喷孔壁面的 冷却作用使火焰传播速度降低；
(2)采用导热性差的材料制造喷嘴，减少喷嘴对燃气 的传热；
(3)对大型喷嘴进行水冷或空冷；
(4)减少一次空气量，增设二次空气，使燃料与一次 空气的混合气偏离化学当量比，使火焰传播速度 降低；
第四节 火焰稳定的原理和方法
第三节 扩散火焰与预混火焰
1、什么叫做扩散火焰和预混火焰？ 2、扩散火焰、预混火焰形状？ 3、扩散火焰和预混火焰有什么特点？
一、扩散火焰和预混火焰的定义：
1、扩散燃烧： 可燃气体从喷口喷出，在喷口处与空气 中的氧气边扩散混合、边燃烧的现象， 称为扩散燃烧。
例如： 管道、容器泄露口发生的燃烧，天然气井
例如： 使用气焊气割时，乙炔和氧气的混合。 本生灯。
本生灯
5、燃烧速度： 取决于可燃气体的浓度、初始温度、管 道直径。
过量空气系数，α ＝0.93；可以大大促进 化学反应速度。
6、预混火焰： 预混燃烧时所形成的火焰。
二、扩散火焰、预混火焰形状：
1、预混燃烧在燃烧前，燃料与氧气已经在 燃烧器内充分混合。它是相对于扩散燃 烧的另一种典型燃烧方式。
防止回火的方法
防止回火的方法：主要是降低喷口处的火焰传播 速度和提高可燃气在喷口处的速度。具体措施有 ：
(1)减小喷口直径，增加喷嘴数量。利用喷孔壁面的 冷却作用使火焰传播速度降低；
(2)采用导热性差的材料制造喷嘴，减少喷嘴对燃气 的传热；
(3)对大型喷嘴进行水冷或空冷； (4)减少一次空气量，增设二次空气，使燃料与一次
对于燃烧装置来说，不仅要保证燃料能顺 利着火，而且还要求在着火后形成稳定火 焰，不出现离焰、吹熄、脱火、回火等问 题，从而具有稳定的燃烧过程。如果着火 后的燃烧火焰时断时续，那么该燃烧装置 就不具备实用价值。

燃烧理论基础-层流预混火焰

燃烧理论基础-层流预混火焰

7.10
对稳定流动 mi mi i=1,2,......,N
1 d
r2 dr
r2mi mi
i 1, 2,......, N
球坐标
二维轴对称坐标
1 r
r
r
vrYA
1 r
x
r
vxYA
1 r
r
r
AB
YA r
mA
(3) 多组分扩散（不讲）
在对燃烧系统的建模和学习理解中，尤其是对层 流预混和非预混火焰结构的研究中，不能用二元混 合物来做简化。在这种情况下，组分的输运公式必 须同时考虑众多且性质差别很大的组分。例如，我 们可以推断，大燃料分子的扩散速度要小于氢原子 的扩散速度。
另外，火焰中典型的大温度梯度，形成了浓度梯 度之外另一个推动传质过程的作用力。这种作用 被称为热扩散或者Soret效应，它使得较轻的分子 从低温处扩散到高温处，相对的，令较重的分子 从高温处扩散到低温处。
多组分扩散的通用性方程
mi,diff mi,diff , mi,diff ,T mi,diff ,P mi,diff , f
2021/4/25
43
能量守恒
Shvab-Zeldovich能量方程
7.63
mc p
dT dx
d dx
( Dcp )
dT dx
h0f ,imi
单位体积内对 流（平流）引 起的显焓变化 速率
单位体积内扩 散引起的显焓 变化速率
单位体积内化 学反应引起的 显焓变化速率
比较
组分A质量守恒
m A
d dx
混合气轴向速度与水平坐标的关系
2021/4/25
14
求解 SL vu sin 8.2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
湍流尺度l： 在湍流中不规则运动的流体微团的平均尺寸，处于宏观量级 若l<δ(层流焰面厚度)为小尺度湍流，反之为大尺度湍流 湍流强度ε： 描述湍流运动的速度为u=U+u’ U为平均速度， u’为瞬时脉动速度，u’=[(u’12+ u’22+…+ u’n2)/n]0.5 流体微团的平均脉动速度与主流速度之比为湍流强度 ε =u’/u 若u’>un（层流火焰传播速度）为强湍流，反之为弱湍流
湍流火焰的特点
均匀、各向同性的湍流流场，可以用两 个特征量表示湍流特征：湍流强度和湍 流尺度
湍流尺度：
（1）流动特征尺度（与管径、绕流物体尺度有关） （2）积分尺度（湍流宏观尺度，大涡尺度） （3）泰勒微尺度（与平均应变率有关） （4）柯尔莫戈洛夫尺度（最小尺度，与旋涡耗散有关）
湍流火焰的特点
小尺度湍流预混火焰传播速度确定
湍流火焰传播速度和层流火焰传播速度之比等 于二者传输率之比的平方根
ut un
T n
1/ 2
T n
/ 0cp / 0cp
1/ 2
λt表示湍流热传导系数 λl表示层流热传导系数 根据相似性原理，分子导温系数α= λn/(ρ0cp), 故 湍流导温系数αt= λT/(ρ0cp)。在湍流中湍流导温 系数取决于湍流尺度和脉动速度乘积，即
a）小尺度湍流火焰（2300<Re<6000） 条件： l<δL
现象：能够保持规则的火焰锋面，火焰前 沿仍然平滑，只是增加了厚度，火焰锋面 不发生皱折，湍流火焰面厚度δT> δn
特点：小尺度湍流只是由于湍流增强了物 质的输运特性，从而使热量和活性粒子的 传输增加，使湍流火焰传播速度比层流火 焰传播速度快，而在其它方面没有什么影 响
ut un
锥体表面积 锥底面积
R
R2 h2
R 2
1 (h / R)2
1 (2h / l)2
式中h为椎体高度，R是湍流尺度的一半，R l / 2
由于湍流微团在锥形表面上的燃烧速度是un ,则微团存在的时间
l / 2un，湍流脉动速度是u, 锥体高度h u ul /(2un )
ut 1 ( u )2
燃烧学
6-湍流预混火焰
湍流预混火焰传播 湍流预混火焰传播图域 湍流预混火焰传播速度确定 湍流火焰传播速度影响因素
第一节 湍流预混火焰传播
研究湍流火焰的目的
（1）工程中的燃烧装置多为湍流燃烧 （2）确定湍流特性对火焰传播的影响 雷诺数Re=ρvL/μ 直管段中： Re<2300时，层流； Re>3200时，湍流 此时火焰为湍流火焰
湍流预混火焰传播可以描述为在湍流流动中传播的薄的层流 预混火焰。湍流流动使火焰发生扭曲，扭曲程度取决于当地 湍流强度
湍流火焰传播速度：湍流火焰前沿法向相对于新鲜可燃气运 动的速度，可用流经火焰的可燃预混气的体积流量除以湍流 火焰的表观面积表示
ST=Q/Af
关键在于确定湍流火焰表面积
由于湍流火焰表面积很难准确测量，一般采 用下面公式计算火焰传播速度
un
un
增大湍流脉动速度，可以提高湍流传播速度
c）大尺度强湍流火焰（Re>6000） 条件： l>δL，u’>SL
现象： 不存在连续的火焰面
大尺度强湍流传播速度确定
湍流强度很大时： u’/un>>1
ut∝u’ 湍流火焰传播速度与化学动力学因素无 关，只取决于脉动速度大小
湍流火焰传播速度
大尺度强湍流火焰（湍流火焰传播的容积理论）
αt∝ lu’
湍流火焰传播速度
对于管流，湍流尺度l与管径成正比，脉动速度u’与 气流速度成正比
l∝d u’ ∝u
而分子导温系数α与运动粘性系数ν成正比，所以
小尺度湍流情况下，湍流火焰传播速度不仅与可燃气 的物理化学性质有关（即与un成正比），还与流动特 性有关（即与Re1/2有关）
b）大尺度弱湍流火焰（Re>6000） 条件： l>δL，u’<SL
现象： 火焰锋面扭曲皱折 火焰锋面未被吹破，仍然是连续的
大尺度弱湍流传播速度确定——小 火焰模型（表面理论）
设薄层焰锋的传播速度仍然是un，那么单位时间内焰锋锋 面烧掉的混合气是Acun，它应与湍流火焰传播速度ut和湍 流焰锋的平均面积Ap的乘积相等，即：
Acun=Aput 或 ut=Acun/Ap 因为Ac>Ap,故ut>un, 若把湍流气团设想成凹凸不平的很多 小的焰锋，则ut>un, 等于这些小的椎体表面积和底面积之 比。 ——小火焰模型，亦称湍流火焰传播的表面理论
湍流火焰的特点
层流火焰： 火焰锋面光滑，焰锋厚度很薄，火焰 传播速度小（20-100cm/s） 湍流火焰 火焰长度缩短，焰锋变宽，并有明显 的噪声，焰锋不再是光滑的表面，而 是抖动的粗糙表面，火焰传播速度快
用Rayleigh激光散射的方法瞬态测量在流动临近平均火焰位 置的特定处的气体密度。
可见气体密度值在未燃气体与已燃气体值之间快速波动，表 明火焰是通过测量位置脉动的薄层
St
m
Au
湍流预混火焰传播速度要比层流预混火焰传 播速度快
湍流火焰比层流火焰传播快的原因
（1）湍流流动使火焰变形，火焰表面积增加，因而增大了 反应区； （2）湍流加速了热量和活性中间产物的传输，使反应速率 增加，即燃烧速率增加； （3）湍流加快了新鲜混合气和燃气之间的混合，缩短了混 合时间，提高了燃烧速度。 湍流火焰理论基于上述概念发展起来的。 湍流火焰传播理论主要有两种： （1）表面褶皱理论（邓克尔和谢尔金） （2）容积燃烧理论（萨默菲尔德和谢京科夫）
大尺度强湍流火焰模型可以设想成大团大团未燃烧的 可燃混合物冲破火焰锋面，而输入高温的燃烧产物中； 大团大团的高温燃烧产物也冲破火焰锋面而输入未燃 烧的可燃混合物中。这些大团的尺寸都超过了层流火 焰厚度，它们在输运之后都保存自己的独立性，一下 子不能和周围气团混合，湍流脉动使火焰迁移到哪里， 就燃烧到哪里，故此时的火焰传播速度可以认为近似 等于脉动速度
第二节 湍流预混火焰传播图域
湍流预混火焰的性质既依赖于预混层流火焰的特性（如SL和
δL），也依赖于湍流的特性，如l和u’
Da=τm/τr
三种湍流火焰模型
湍流火焰
小尺度湍流火焰 l<δL 大尺度弱湍流火焰u’<SL
大尺度湍流火焰 l >δL
大尺度强湍流火焰u’>SL
第三节 湍流预混火焰传播速度确定Байду номын сангаас